基于随机共振的滚动轴承故障诊断研究*

郑 煜，赵俊豪

(陕西工业职业技术学院 机械工程学院，陕西 咸阳 712042)

0 引言

随机共振(Stochastic resonance, SR)于1983年由Benzi R在研究气候变化时发现，该现象是布朗粒子在双稳态势阱中，受周期策动力和噪声共同作用下表现出的一种非线性现象，双稳态随机共振故障诊断方法目前在光伏设备[1]、图像处理[2]、信号检测[3,4]和信号增强[5,6]等领域都有广泛的应用。滚动轴承是旋转机械的核心部件，其运行是否正常往往直接影响机械设备的运行状态，因此对于关键轴承的故障诊断就显得尤为重要。

本文使用双稳态随机共振的诊断手段，将内滚道故障轴承振动数据输入双稳态系统引发随机共振，通过研究输出信号的幅值谱，实现了滚动轴承的故障诊断并验证了随机共振诊断法的有效性。

1 随机共振

随机共振现象可由郎之万方程(Langevin’s equation, LE)描述，即：

(1)

其中：x(t)为布朗粒子的位移，即系统的输出；U(x)为双稳态势函数，U(x)=-(a/2)x2+(b/4)x4，a、b为结构参数；s(t)为周期策动力，即输入信号；ξ(t)为强度为D的高斯白噪声，〈ξ(t),ξ(0)〉=2Dδ(t)，δ(t)为单位阶跃函数。

结构参数a、b决定了势函数U(x)的分布形式，a=2、b=1条件下的双稳态势函数U(x)形态如图1所示。

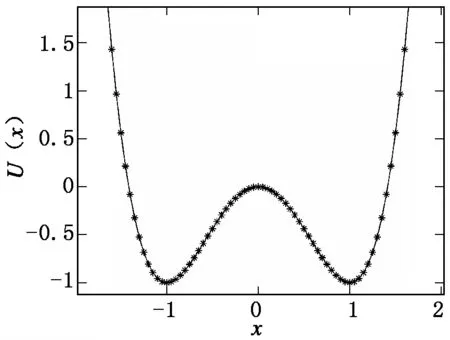
图1 a=2、b=1下的双稳态势函数U(x)形态

随机共振现象具体可表述为：当周期策动力—噪声—非线性系统(双稳态系统)达到某种协同时，布朗粒子的输出信噪比可得到改善。因此，将滚动轴承的故障振动信号输入双稳态系统引发随机共振，从而改善输出信号的信噪比以实现故障诊断。

2 实测数据故障诊断

2.1 实验数据

本文实验数据使用美国凯斯西储大学滚动轴承故障探伤数据[7]，实验装置如图2所示。测试台由2马力(1马力=735 W)电机(左)、扭矩传感器/编码器(中)、测功机(右)和控制电子设备组成，测试轴承支撑电机轴，在靠近和远离电机端轴承的位置测量加速度数据。

图2 实验装置

轴承型号为6205-2RS JEM SKF，使用电火花分别在电机端轴承内滚道、外滚道或滚动体产生点蚀故障。内滚道、外滚道或滚动体上的故障单独存在，无复合故障。本次实验数据获取自内滚道存在故障轴承且电机不承受载荷、转速为1 797 r/min时，靠近电机端轴承加速度传感器测得的振动数据。使用16通道数字录音记录器采集加速度传感器数据，采样频率为12 kHz。

2.2 故障诊断

设计双稳态势函数U(x)，结构参数a=0.987、b=0.087。选取点蚀凹坑直径为0.53 mm的轴承振动数据作为故障数据。将故障数据输入双稳态势函数，引发随机共振现象，使用4阶Runge-Kutta法求解郎之万方程得到输出信号。输入信号及其幅值谱如图3所示。

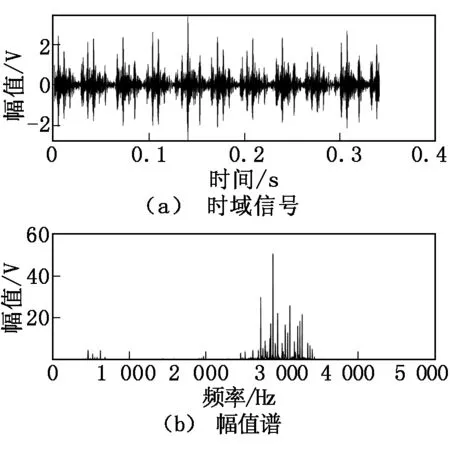
图3 输入信号及其幅值谱

从图3可以看出：输入信号的幅值谱在可能存在故障频率成分的低频段内几乎看不到峰值，说明对于故障数据如果仅通过幅值谱是很难确定是否存在内滚道故障的。输出信号及其幅值谱如图4所示。

图4 输出信号及其幅值谱

从图4可以看出：将故障数据输入双稳态势函数引发随机共振后，输出信号幅值谱在低频段内161.1 Hz处存在明显的故障频率成分。

故障特征频率计算公式为：

(2)

其中：N为轴承滚动体个数；d为滚动体直径，mm；D1为轴承节径，mm；α为轴承接触角，(°)；f为轴承转动基频，Hz，f=n/60,n为内圈转速，r/min。轴承6205-2RS JEM SKF结构参数如表1所示。

表1 轴承6205-2RS JEM SKF结构参数

将数值代入式(2)计算得：故障特征频率fip=162 Hz。计算结果与图4中结果相同，表明本文方法是有效的。

3 结论

本文选择双稳态随机共振作为滚动轴承早期故障的诊断方法。首先介绍了双稳态随机共振的产生原理；随后选择凯斯西储大学滚动轴承故障探伤数据作为本文实验数据并介绍了实验装置和相关实验参数；使用内滚道故障轴承数据作为待诊断数据，将故障数据输入双稳态系统，引发随机共振现象，分别求取输入信号、输出信号的幅值谱，通过观察可以看出:输出信号幅值谱在161.1 Hz处存在明显的故障成分，而输入信号在低频段很难观察到频谱峰值，验证了该方法的可行性。