基于偏振光的无人机航姿LM优化解算方法*

孙庆飞，金仁成，刘 忱，黄启鹏

(大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024)

0 引言

传统组合导航系统多是以由陀螺仪和加速度计组成的惯导单元为基础，结合磁力计和GPS来实现无人机航姿解算、导航和定位[1]。虽然GPS及磁力计能够在很大程度上提高导航系统的姿态角解算精度并获得航向信息，但这两种传感器都极易受到自身机载电路及周围电磁场的干扰，军事上GPS甚至会受到敌方的攻击与诱导，失去工作能力。因此，近些年针对无人机导航系统抗干扰和自主性的研究成为行业热点，具有无源自主特点的仿生传感器也在导航领域得到了应用和推广。

偏振光传感器仿照蜜蜂、沙蚁等生物利用大气偏振分布进行导航寻踪，获取太阳光经过大气散射之后产生的偏振信息替代GPS或磁力计，辅助惯导系统完成航向信息的获取与解算，具有自主性、不受电磁等外在干扰的优势[2]。2012年，澳大利亚学者Chahl J等[3]对固定翼无人机进行了偏振导航实验。2014年，中科大与中科院先进制造所将偏振光传感器加载至车载导航系统[4]。2020年，蔚彦昭[5]设计了梯度及共轭梯度算法，有效提高了偏振光与微惯导组合导航系统的姿态解算精度。

本文引入列文伯格-马夸尔特(Levenberg-Marquardt，LM)算法，对偏振光传感器和惯导元件输出值进行融合与求解，获得三维姿态角信息。并通过实验验证了所提LM法相较于梯度法(GG)、共轭梯度法(CG)以及牛顿法(Newton)具有更稳定的静态性能和更小的动态解算误差。

1 太阳偏振光定姿模型

1.1 三维坐标系分布

设载体坐标系为b系，导航坐标系为n系，惯性坐标系为i系，地球坐标系为e系，无人机的姿态切换主要是载体坐标系(b系)和导航坐标系(n系)之间的坐标变换。在太阳偏振光测量模型中引入偏振传感器坐标系(m系)和太阳坐标系(p系)。各坐标系的位置关系及偏振光测量模型如图1所示。

图1 各坐标系位置关系及偏振光测量模型

图1(b)中,瑞利散射最大偏振矢量E始终垂直于太阳矢量S和观测矢量Z所构成的平面，据此创建偏振光理论测量模型。

1.2 偏振角定姿原理

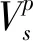
(1)

(2)

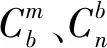
(3)

2 基于LM的航姿优化解算方法

LM法是使用最广泛的非线性最小二乘算法之一，是利用梯度求最大/小值的算法，同时具有梯度法和牛顿法的优点。无人机在静止或匀速环境中，通过加速度计和偏振光传感器获取实测重力和偏振矢量，由惯性导航原理与偏振矢量导航原理算得理论重力矢量和理论偏振矢量，通过理论与实测之差构造目标函数，并通过LM优化理论求解目标函数在局部最小值时的解作为最优的四元数解，补偿陀螺仪输出值，进而解算出最终姿态估计值。

2.1 矢量误差函数

(4)

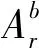
(5)

(6)

由重力和偏振模型组合获得综合误差函数F及其对应的雅克比矩阵J，进一步获得函数梯度F：

(7)

2.2 LM优化解算方法

LM法是一种非线性无约束最优化算法，利用该算法对无人机的航姿进行解算对其飞行过程中受到的噪声干扰和陀螺仪漂移问题具有明显抑制作用，不需要考虑非线性模型转换成线性的问题。LM法使用的梯度方向与GG、CG等算法相同，将函数梯度F作为收敛方向，其中步长λk的选取类似于高斯牛顿法，由JTJ求得，为了避免出现奇异性，加入了调节因子μ，即：

λk=(JTJ+μI)-1.

(8)

其中：I为四阶单位矩阵。

调节因子μ的取值决定了算法的收敛方式，μ值较大时收敛过程与GG相似，使求解函数快速收敛至目标点;μ值较小(接近于零)时几乎与高斯牛顿法相同，以减慢下降速度，使收敛平稳进行。μ的调整是通过参数ρ实现的：

(9)

ρ的分子部分为求解函数实际的下降速率，分母部分可看作求解函数下降速率的近似值。ρ值大于0时，尤其ρ值接近1时，表明近似值可信，减小μ值，增大步长；ρ小于0时，表明近似值不准确，增大μ值，缩短步长。

得到μ值后，重新计算步长λk，更新四元数微分方程，获得最终姿态四元数：

(10)

3 实验验证与结果分析

3.1 飞控平台

实验飞控系统测量单元搭载惯导单元MPU6000、磁力计HMC5883和偏振光传感器。将飞控系统放置于精密转台上进行测试实验，以惯导单元和磁力计输出姿态信息为参考值，与转台精确姿态输出值进行对比，验证参考值的准确性。精密转台测试结果如图2所示。

图2 精密转台测试结果

由图2(b)误差曲线可知，飞控系统输出误差小于1°，可以将其作为参考值。本文使用LM算法融合惯导与偏振光求解三维姿态角，将解算值与参考值对比，验证LM算法可靠性。在大连理工大学机械工程学院东楼楼顶(121.528 255 °E，38.881 419 2°N)分别进行静态和动态实验。

3.2 静态实验及分析

2021年5月21日下午17：29，晴，查天文历表得知：太阳方位角18.41°，太阳高度角-78.43°。将飞控平台置于地面360 s，静态解算结果如图3所示。

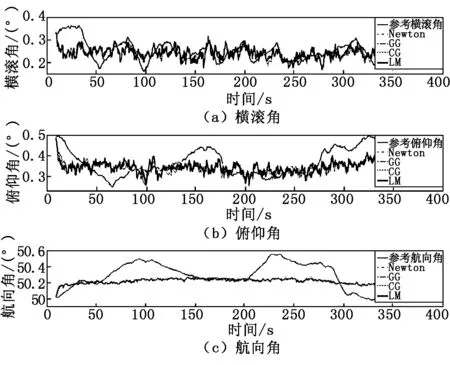
图3 静态解算结果

为了更直观地查看各方法解算效果，得到静态环境下各算法所求姿态角的均值和方差，如表1所示。

表1显示，Newton法作为稳定收敛算法，在静态性能上具有一定优势，而LM算法静态特性好于GG、CG等梯度算法，接近于Newton法，求解均值接近参考均值，且具有更小的均方差。

表1 静态环境下姿态角均值与方差 (°)

3.3 动态实验及分析

2021年5月21日下午18:05，晴，查天文历表得知：太阳方位角11.63°，太阳高度角-73.23°。将飞控平台置于转动空间220 s，动态解算结果如图4所示，动态解算误差曲线如图5所示。

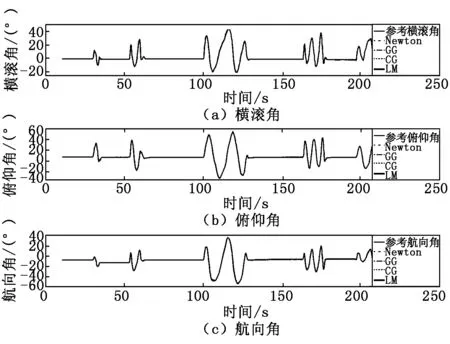
图4 动态解算结果

图5显示，LM动态解算精度相较于其他三种算法的横滚角、俯仰角和航向角分别至少提升51.7%、40.9%和44.7%。

图5 动态解算误差曲线

4 结论

本文将LM算法应用到基于偏振光和惯导的组合导航系统，解算的三维姿态信息在静态环境中具有良好的稳定性，能有效滤除机体噪声带来的扰动干扰；相较于传统算法，动态性能有了40%以上的提升，为提高组合导航系统姿态解算性能提供了一种可靠的算法参考。

因为矢量误差模型是在无非重力加速度干扰情况下构建的，所以在实际飞行过程中加速度的产生会影响解算精度，下一步工作将重点研究如何降低非重力加速度对误差模型的干扰。