大气隙外笼型转子磁力耦合器分析及优化*

葛研军,杨 博,刘振晗,权世成

(大连交通大学 机械工程学院，辽宁 大连 116028)

0 引言

永磁磁力耦合器通过永磁转子与导体转子的磁场耦合实现无接触传动，具有软启动、过载保护、隔离振动及适应恶劣环境等优点[1]，作为主要应用于电机与负载之间的新型传动及调速装置，在诸多领域被广泛应用[2]。

为提升磁力耦合器性能对其进行优化设计，试验的方法耗费巨大，有限元仿真耗时长且不能得到优化规律[3]。本文采用响应面优化方法(Response Surface Methodology，RSM)中最常用的Box-Behnken Design(BBD)进行试验设计，通过多元二次回归方程拟合，得到各因素与优化目标的方程表达式，并据此进行优化设计，减少了仿真数量，不仅考虑了试验误差，而且可对复杂的未知函数关系在一定范围内通过二次多项式进行连续拟合，具有实际指导意义，可大大提高优化设计效率[4-7]。

建立大气隙磁力耦合器有限元模型，通过 Ansoft仿真软件分析永磁转子与导体转子的结构参数对电磁转矩的影响，采用RSM结合Design Expert软件分析各参数影响效果，并拟合回归方程得到主要结构参数与电磁转矩关系式，从而对大气隙外笼型转子磁力耦合器(LAEMC)进行优化设计。

1 LAEMC的结构及主要参数

1.1 LAEMC结构模型

大气隙外笼型转子磁力耦合器(Long Air Gap External-cage Rotor Magnetic Coupler，LAEMC)为永磁转子与导体转子间有10 mm长度气隙的筒式结构磁力耦合器，其结构如图1所示。LAEMC主要由永磁转子与导体转子组成，其中永磁转子由径向与切向磁化永磁体交替排列组成的Halbach阵列和内轭铁组成，导体转子由鼠笼和外轭铁组成。LAEMC的Halbach阵列结构具有聚磁特性[8,9]，其所产生的永磁磁场通过气隙在导体转子产生感应电势和感应电流，再由感应电流与永磁磁场相互旋转切割磁感线产生电磁转矩，使得两转子同向旋转实现动力传动。

图1 LAEMC结构图

LAEMC中永磁体作为磁源产生磁动势，经由气隙及内、外轭铁形成磁回路。导体转子与永磁转子旋转运动，在笼条导体内产生感应电流，永磁磁场与笼条感生磁场相互耦合产生电磁转矩。磁回路中气隙及笼条磁阻较大，而轭铁的磁阻很小，磁阻与各结构尺寸参数有关，共同作用影响LAEMC传递的电磁转矩及产生的涡流损耗大小。通过优化各结构尺寸参数，可增大磁动势、减小磁阻，产生更大的电磁转矩。

1.2 关键结构参数

根据设计要求建立LAEMC有限元分析模型，在保持气隙长度为10 mm及整体体积不变的前提下，通过改变各结构参数仿真得到对应的电磁转矩，分析各结构参数的影响效果。

LAEMC主要结构参数示意图如图2所示,包括鼠笼槽型的槽口宽Bs0、槽心宽Bs1、槽底宽Bs2、槽底圆半径Rs、槽颈高Hs0、槽宽高Hs2及Halbach阵列永磁体的厚度h、Halbach磁化比α/β。

图2 LAEMC结构参数示意图

2 结构参数影响分析

2.1 主要结构尺寸参数

通过Ansoft 有限元软件对LAEMC进行参数化建模，在保持其他结构尺寸不变的前提下，按表1所示各结构尺寸参数初始值及变化范围，通过瞬态仿真得到其电磁转矩，仿真结果如图3所示。

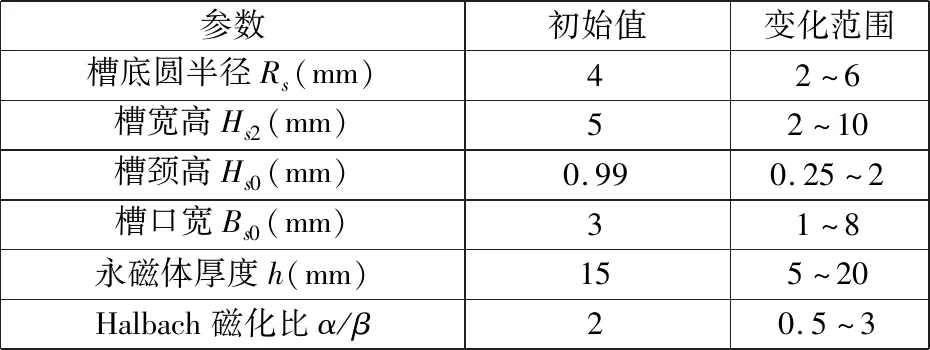
表1 结构参数初始值与变化范围

2.2 结构参数影响分析

分析图3中LAEMC电磁转矩随各参数变化：图3(a)中电磁转矩随槽底圆半径的增大先逐渐增加后减小，在Rs=5 mm时达到最大为319 N·m；图3(b)电磁转矩随槽宽高的增大先增加后减小，在Hs2=6 mm处达到最大约为310 N·m；图3(c)中电磁转矩随槽颈高Hs0的增大变化不大，说明Hs0的影响较小；图3(d)中电磁转矩随槽口宽Bs0增加而增大，在Bs0=8时达到345 N·m，影响效果明显；图3(e)中电磁转矩随永磁体厚度h增加而显著增加，当h=20 mm时为372 N·m，说明永磁体厚度增加可产生更强的永磁磁场；在图3(f)中电磁转矩随永磁体Halbach磁化比的增加变化显著，范围为249 N·m～323 N·m，Halbach结构的聚磁特性可大大提高单侧磁场强度，永磁体磁化比可以增加LAEMC电磁转矩，从而减小所需永磁体体积。

图3 各结构参数与电磁转矩关系

3 响应面优化法设计优化

结合以上分析，为提高电磁转矩T，选取表2中对电磁转矩影响显著的4个结构参数进行优化设计分析，各参数设计变量因素与水平变化范围如表2所示。

以表2所示设计参数变量作为约束，建立LAEMC的优化分析目标函数，通过Design Expert软件中BBD优化设计方法设计试验方案并进行仿真分析。

表2 设计变量因素与水平

3.1 优化试验结果分析及目标拟合

通过对试验仿真结果拟合得到优化目标响应值与设计变量回归方程，电磁转矩为：

由上式可以看出：x1、x3、x4的影响显著，且x1、x3交互作用明显。

3.2 响应面分析

根据电磁转矩T回归方程，选取系数较大的结构参数分析其对响应值的交互影响作用，得三维响应面图如图4所示。

由图4(a)可知：槽口宽Bs0的变化对电磁转矩影响更大，随着槽口宽Bs0增加，电磁转矩先显著增加后逐渐变化平缓；而随着槽宽高Hs2增加，电磁转矩先增加后减小，这是因为整体结构尺寸保持不变，随着槽宽高Hs2增大，外轭铁厚度相应减小，产生磁饱和致使磁通量减小。

由图4(b)可知：槽口宽Bs0较Halbach磁化比对电磁转矩影响更大。Halbach磁化比增加也就是图2中永磁体径向磁化圆周角度α增加而切向磁化圆周角度β随之减小，从而提高聚磁效果产生更大的磁场强度。

由图4(c)可知：槽宽高Hs2与Halbach磁化比对电磁转矩的影响效果都很显著，Halbach磁化比增加使永磁磁场强度增加，槽宽高Hs2增加使笼条截面积变大，可以增加感应电流强度，二者耦合强度增加从而电磁转矩增加，可带动更大转矩的负载。

图4 双因素响应曲面三维图

4 优化结果与验证

4.1 优化结果

通过Design Expert软件设置求解最优目标maxT，得到最大转矩对应结构参数为Bs0=7.64 mm、Rs=3.99 mm、Hs2=6.19 mm、α/β=2.44，此时电磁转矩为388.44 N·m，较初始参数结构的电磁转矩324.22 N·m提升19.8%。

4.2 响应面优化结果仿真验证

通过Ansoft软件按Design Expert 软件拟合得到的最优结构参数建模并仿真，对应电磁转矩为383.36 N·m，与拟合结果相差1.3%，此时较初始参数结构的电磁转矩提升18.2%，验证了由Design Expert所得拟合方程及最优解的准确性，有效提高了LAEMC电磁转矩。

5 结论

(1) 采用响应面法对LAEMC进行优化设计，结合Design Expert软件不仅提高了优化设计效率，且通过回归方程拟合得到LAEMC电磁转矩方程表达式。

(2) 通过拟合方程得到LAEMC电磁转矩最优解，并通过有限元仿真验证，将LAEMC电磁转矩提高了18.2%，证明该方法切实可行，为以后的优化设计提供了参考。