预报单向复合材料轴向强度的双尺度方法
2022-06-24唐绍锋
唐绍锋
(中国运载火箭技术研究院,北京 100076)
0 引言
复合材料以其优异的力学性能(高比强度、高比刚度等)在航天技术领域得到了广泛的应用,故对复合材料的宏观性能表征和破坏机理的研究是十分必要的。然而,当使用有限元法(FEM)直接分析上述问题时,由于复合材料的细观非均匀性,需要一个非常精细的网格来识别不同的组分。因此,细化网格所带来的巨大计算量使得分析难以实现。
克服这一困难的一个自然方法是用一种等效的均质材料模型代替复合材料。“均匀化”的概念是由Babuska[1]最早提出的。自20世纪70年代以来发展起来的均匀化数学理论,被用作寻找等效均匀化材料有效性能的替代方法,该等效均匀化材料用周期性细观单胞取代原始复合材料[2-5]。在该方法中,复合材料结构由均匀宏观结构和非均匀细观单胞进行描述。所有量都表示为细观坐标和宏观坐标的函数,并展开为渐近级数,然后通过积分在单胞内得到复合材料的有效性能。基于均匀化理论对复合材料的有效刚度和弹性模量进行了预报,预报结果与实验值或其他数值方法的计算结果吻合良好[6-7]。此外,复合材料的有效热常数(如导热系数和热膨胀系数)也可以通过均匀化理论进行预测[8-9]。上述研究表明,均匀化理论可以有效地预测复合材料的宏观均匀化有效性能。
然而,只有宏观均匀化应力场不足以预报复合材料的强度。因此,基于均匀化理论,学者们提出了具有周期性细观单胞的复合材料的双尺度渐近分析方法[10]。其主要思想是在从细观到宏观的过程中,用双尺度均匀化方法计算复合材料的性能;然后在从宏观到细观的过程中,用双尺度渐近技术描述物理场和力学场的局部起伏。近几十年来,许多数学家和力学学者用这种方法分析了复合材料的局部响应[11-16]。这些工作验证了描述复合材料应力场的双尺度渐近分析方法的有效性和高效性。应力场的正确描述是分析材料失效的基础。余新刚对基于双尺度渐近分析方法预报两相复合材料的强度进行了有益的尝试[17]。
本文基于双尺度渐近分析方法,根据组分材料的不同属性引入不同的强度准则,建立了预报单向复合材料轴向强度的双尺度方法。在第1中,根据组分材料的不同属性,分别为增强体(纤维)和基体引入了不同的强度标准。第2给出了单向复合材料在宏观轴向均匀载荷下应变的简化双尺度表达式,并结合第3中引入的准则,得出了单向复合材料轴向强度的计算公式。第3提供了预报单向碳纤维增强环氧树脂基复合材料轴向强度的数值算例。该方法可以直接计算单向复合材料的轴向抗压强度;并通过定义纤维有效拉伸强度的概念计算单向复合材料的轴向拉伸强度(纤维有效拉伸强度是通过统计学计算得到的)。最后,在第4中给出了本文的结论。
1 细观强度准则
到目前为止,还没有专门针对复合材料的失效准则。因此,复合材料的失效只能通过细观尺度上各组分材料的失效来判断。一般来说,增强体和基体具有不同的材料属性,因此应根据它们的不同属性选择不同的强度准则。
1.1 增强体(纤维)
在宏观轴向均匀拉伸载荷下,单向复合材料的纤维失效模式为纤维断裂,如图1所示。假设在宏观轴向均匀压缩载荷下,纤维的失效模式也是断裂(这里忽略纤维屈曲失稳)。考虑到纤维的脆性特质,采用最大主应力断裂准则作为纤维的强度准则。对均匀材料来说,该准则表述为当最大主应力超过材料的弹性极限时材料即发生断裂。
一般来说,对于轴向载荷下的纤维,其断裂是贯穿纤维横截面的(图1)。这里轴向正应力即最大主应力,所以纤维的强度准则表述为:

图1 单向碳纤维增强环氧树脂基复合材料中纤维断裂的扫描照片
(1)
其中σaT为拉伸时的纤维轴向正应力,σaC为压缩时的纤维轴向正应力(的绝对值),SfT为纤维的轴向拉伸强度,SfC为纤维的轴向压缩强度。
1.2 基体
本文中的基体为环氧树脂。因为基体是韧性材料,这里采用形变能准则(第四强度理论),形式如下:
(2)
其中σe为基体材料的Mises等效应力,Sm为基体材料的屈服强度,σ11,σ22,σ33,τ12,τ23以及τ31为确定一点应力状态的6个应力分量,脚标1, 2以及3分别表示两个横向以及轴向。
当(2)式不成立时,基体材料即为失效状态,即认为复合材料失效。
2 轴向均匀载荷下单向复合材料轴向强度的双尺度表达式
2.1 具有周期性结构的复合材料的双尺度渐近表述
对于具有周期性细观单胞的复合材料,如果单胞结构是对称的,由参考文献[13]可以证明,复合材料的实际位移可以近似表示为:
(3)
其中x和y分别是宏观(全局)坐标和细观(局部)坐标。定义ε为一个小参数,表示细观坐标系中单位向量的实际长度与宏观坐标系中单位向量的实际长度之比,即y=x/ε。u[0](x)是位移的均匀化解。Nα1(y)和Nα1α2(y)(α1,α2=1,2,3)是三阶函数矩阵,它们被称为基函数,在单胞中求解。它们的解仅依赖于单胞的信息,而不依赖于宏观结构或载荷。
上述函数定义如下(具体见参考文献[12])。

(4)
其中Cijhk(y)是复合材料各组分材料的刚度系数,Q是细观单胞占据的域;εij(v)定义为:
(5)
(6)

(7)

(8)
其中fi为体力,Ω是复合材料结构占据的域。
(5)结构Ω内部任意一点x处的应变和应力可以用下式近似计算:
(9)

σij(x)=Cijhk(y)ehk(x)
(10)
2.2 宏观轴向均匀载荷下单向复合材料轴向强度的表达式
如图2所示,对于在宏观轴向均匀拉伸(或压缩)载荷作用下的单向纤维增强树脂基复合材料柱体,其均匀化位移解可表示为:

图2 单向纤维增强树脂基复合材料的轴向均匀拉伸(压缩)
(11)
其中E11,E22,E33,μ13和μ23为复合材料在三个主轴方向上的宏观有效工程常数。由式(3),位移可以精确表达为:
(12)
由此可以得到各应变分量的表达式:
=pη11
(13-1)
=pη22
(13-2)
=pη33
(13-3)
=pη12
(13-4)
=pη13
(13-5)
=pη23
(13-6)
即有:
[e11,e22,e33,e12,e13,e23]T=p[η11,η22,η33,η12,η13,η23]T
(14)
对增强纤维来说,纤维的轴向正应力σf33的表达式如下:
=pζf
(15)

pf-cri=Sf/ζf
(16)
对基体来说,在外载作用下基体的应力表达式为:

(17)
其中Cm为基体刚度矩阵。基体的Mises等效应力σme为:

(18)
其中ζm为基体的载荷因子。假设基体的屈服强度为Sm,当σme=Sm时,可以求得基体屈服时的临界载荷pm-cri:
pm-cri=Sm/ζm
(19)
最终复合材料的轴向拉伸(压缩)强度Sa应是纤维破坏时的临界载荷pf-cri和基体屈服时的临界载荷pm-cri中较小的那个,即:
Sa=min(pf-cri,pm-cri)
(20)
2.3 预报轴向强度的双尺度方法的计算步骤
(1)在单胞内由式(4)用有限元方法计算基函数Nα1(y)。
(2)在单胞内基于基函数Nα1(y)由式(6)计算复合材料的均匀化刚度系数。
(3)由式(21)将均匀化刚度系数转换为复合材料的工程常数:
(21)
其中S为复合材料的柔度系数,E11,E22,E33,μ13,μ23,μ12,μ31,μ32,μ21,G13,G23和G12为复合材料的有效工程常数。刚度系数与柔度系数的关系为:
I=CH·S
(22)
其中I为单位矩阵,CH为均匀化刚度系数。
(4)假设宏观轴向均匀拉伸(压缩)载荷p=1,由式(13)、(14)、(15)、(17)和(18)分别计算载荷系数ζf和ζm;
(5)最后由式(16)、(19)和(20)计算轴向拉伸(压缩)强度。
3 算例
使用该方法预测纤维体积含量Vf=60%的单向碳纤维增强环氧树脂基复合材料的轴向压缩强度和拉伸强度。
3.1 有效工程常数的计算
为单向复合材料构建了两个具有代表性的细观单胞:长方体单胞(单胞1)和六棱柱单胞(单胞2),如图3所示。基体为各向同性材料,而纤维为横观各向同性材料。组分材料的性能参数见表1。

表1 单向碳纤维增强环氧树脂基复合材料各组分材料性能
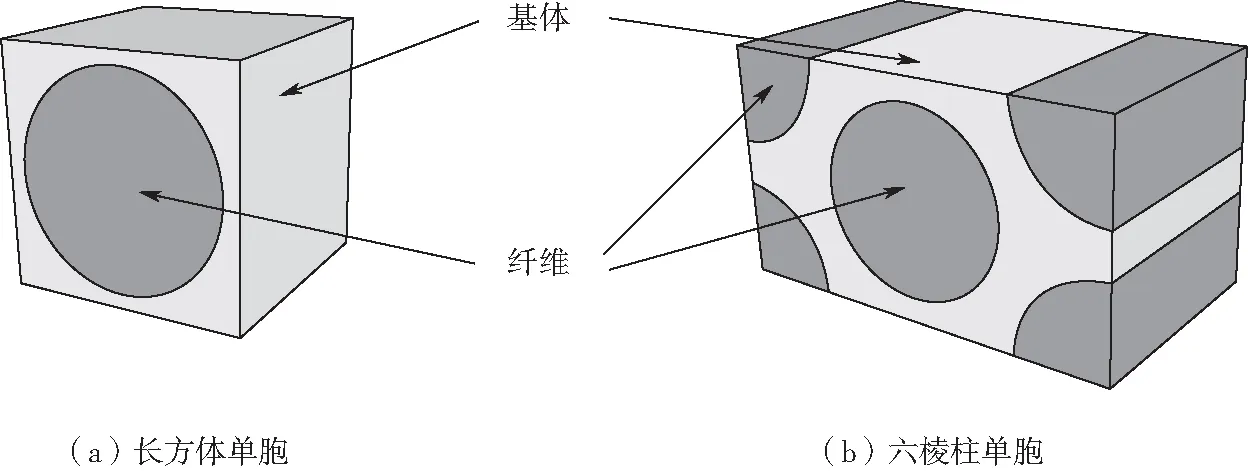
图3 单向复合材料的细观单胞
表2列出了用两个单胞计算的单向碳纤维增强环氧树脂基复合材料的有效工程常数。

表2 用两种单胞计算的有效工程常数
3.2 轴向压缩强度
基于上述有效工程常数,用两个单胞计算了单向碳纤维增强环氧树脂基复合材料的轴向压缩强度。计算值和实验值如图4所示。可以看到两个单胞的计算值和实验值的相对误差分别为14%和12%。我们认为,计算值与实验值之间的差异是由于只考虑了最大应力准则,而忽略了复合材料在轴向压缩下的纤维屈曲。

图4 单向碳纤维增强环氧树脂基复合材料的轴向压缩强度(Vf=60%)
3.3 轴向拉伸强度
由于复合材料中纤维的强度具有较大的分散性,当复合材料承受轴向拉伸载荷时,较弱的纤维将首先发生破坏;随着外载的增加,剩余未破坏的纤维将陆续破坏,直至复合材料失效,即单向纤维增强复合材料受轴向拉伸时的破坏是一个渐近损伤的过程。而采用双尺度方法预报复合材料的强度是在细观单胞内进行的,只要单胞内的任意纤维破坏,就意味着复合材料结构内的所有纤维都破坏了,即复合材料失效。所以采用双尺度方法计算复合材料拉伸强度时,计算所用的纤维的强度应该是一种平均的等效的强度,这个值应该是当复合材料破坏时所有纤维所承受的应力的平均值。


假设纤维的强度分布是Weibull分布:
F(σ)=1-exp(-αδσβ)
(23)
其中α为Weibull尺寸参数;β为Weibull形状参数;δ称作无效长度,其物理意义是指纤维一处断裂后,纤维所承担的应力由零基本恢复至外加载荷所需的长度,定义式为:
24)
其中df为纤维的直径;Vf为纤维体积分数;Ef为纤维轴向模量;Gm为基体剪切模量;φ为载荷恢复程度函数,取值范围为0~1。
假设在外载p的作用下,复合材料内总纤维数为N,其中有Nf根纤维断裂,Nh根纤维没有断裂。当载荷增加dp,平均应力增加dσ,断裂纤维数目增加dNf。根据统计方法,断裂纤维数目和增加的应力满足如下微分方程:
(25)
其中a为与一根断裂纤维相邻的纤维数目;K为与一根断裂纤维相邻的纤维的应力集中因子,a=4或6时,K=1.146或1.104;F(Kσ)为考虑应力集中的纤维破坏概率。
式(25)的初始条件为:
Nf(0)=0
(26)
可以解得:
Nf=Nexp[(a+1)exp(-αδσβ)-aexp(-αδmσβ)]T
(27)
其中:
(28)
所有纤维所承受的轴向应力的平均值为:
(29)

(30)

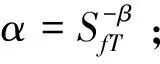
使用双尺度方法计算的单向碳纤维增强环氧树脂基复合材料(Vf=60%)的轴向拉伸强度的计算值和实验值如图5所示。计算值与实验值的相对误差均小于1.6%。轴向拉伸强度的计算值与实验值吻合得很好。

图5 单向碳纤维增强环氧树脂基复合材料的轴向拉伸强度(Vf=60%)
4 结论
根据单向复合材料组分材料的不同属性引入不同的强度准则,建立了预报单向纤维增强复合材料轴向强度的双尺度方法。当应用该方法预报轴向拉伸强度时,引入了纤维有效拉伸强度的概念,将渐近损伤理论与该方法联系起来。结果表明,计算值与实验结果吻合较好,从而验证了该方法的有效性。
