线场分析法在断续周期裂纹岩体拉伸断裂破坏中的优化应用
2022-06-24唐红梅周福川
唐红梅,周福川,闫 凝,商 超
(重庆交通大学 岩土工程研究所,重庆 400074)
0 引 言
从A.A.GRIFFITH[1]采用能量理论研究材料的断裂行为开始,断裂力学已经发展了一个世纪。N.I.MUSKHELISHVILI[2]和H.M.W. WESTERGAARD[3]采用复变函数理论得出了两种应力函数,为断裂力学的发展提供了数学支撑。G.R.IRWIN[4]提出应力强度因子理论后,极大地加速了线弹性断裂力学的发展,此后寻找应力强度因子便成为线弹性断裂力学问题的重点和难点。
求解无限大裂纹体应力强度因子的方法已经出现很久,但是实践中的裂纹体很少呈现无限大形式,绝大部分属于有限边界形态,因此将无限大裂纹体模型的研究成果扩展到有限裂纹体模型具有现实意义[5]。但目前对有限裂纹体模型的解析方法研究仍显不足,且多采用数值计算方式代替,例如M.GONZALEZ 等[6]采用边界元法分别求解了基于能量释放率理论和围道积分等数学公式的数值解;A.S.KOBAYASHI等[7]采用边界配置法得到了有限大裂纹体的应力强度因子数值解;段树金等[8]利用边界配置法求解了含一切口的简支梁在分布荷载作用下的应力强度因子;袁浩等[9]采用有限元手段对J积分、相互作用积分和位移外推法进行数值计算。不过数值分析仍然是一种近似解,不能完全取代理论上的真值。因此,开展有限裂纹体的断裂理论研究属于基础科学研究范畴,仍是断裂力学研究的一个重要方向。
洪起超[10]总结了不同条件下的无限边界模型,整理了一些重要的应力强度因子解析式;郑涛等[11]利用复杂的复变函数方法,推导出带3条共线裂纹模型的解析解;高常辉等[12]利用复变函数方法求解了I型裂纹受面力作用的应力强度因子解析解。复变函数分析方法的复杂性也制约了断裂力学在其他学科领域的推广应用。易志坚[13]采用积分运算,提出的裂纹线场分析法是具有严格力学意义的实用可靠方法。
有限裂纹体断裂问题十分普遍,许多岩体的破裂现象可以视为岩体拉伸破坏的力学行为,如高陡边坡演化过程中坡肩拉应力集中形成拉裂面,以及在大地构造应力作用下岩层横向纵弯导致背斜核部发育断续或连续结构面的岩体拉断破裂现象,其本质上均为拉伸下的岩体断裂问题。将含有断续结构面岩体简化为断续周期裂纹有不同称谓,如非贯通断续节理[14]、共线等间距裂纹[15]或共线等距等长裂隙[16],其主要针对边坡、危岩等地质体,但采用优化后的线场分析法探讨背斜核部拉应力区裂纹的地质现象尚无报道。岩体拉伸断裂破坏涉及拉伸强度问题,A.H.GHAZVINIAN等[17]发现节理的拉伸强度对岩体剪切行为具有显著影响,据此修正了巴顿公式;I.VANICEK[18]通过工程案例展示了拉应力在地质工程领域的重要性,并系统介绍了岩石拉伸破坏试验和发展方向;FENG Gan等[19]基于周向应力理论和试验拟合得出了不同温度下断裂韧度和拉应力强度之间的关系;郭芳等[20]采用数值模拟方法对节理岩体边坡稳定性进行分析,得出了考虑岩体拉伸破坏更加符合实际情况的结论。然而,线场分析法在岩体拉伸强度方面的应用罕见。笔者采用优化后的线场分析法研究背斜核部岩体在单向拉伸作用下的断裂破坏机制,由地质模型概化出断续周期裂纹模型,获取中心裂纹力学模型;引入线场分析法,通过应力修正值和形状修正系数研究背斜核部岩体拉裂纹拉伸断裂问题,对解译背斜核部岩体拉断破裂现象和工程岩体拉伸强度问题等方面具有实际意义。
1 断续周期裂纹岩体地质力学模型
背斜核部拉应力区裂纹具有以下主要特征:发育在岩体内部;以非连续分布形式展现;一组结构面包含多条平行非贯通结构面,一条结构面又由许多断续裂纹组成;断续裂纹以等距或非等距共线排布;裂纹长短随机组合(图1)。笔者据此提出背斜核部岩体的“断续周期裂纹”模型(图2)。

图1 背斜核部拉应力区裂纹实物Fig. 1 Diagram of crack in tensile stress zone of anticline core
图2(a)为地层背斜核部地质剖面示意。在区域上受水平构造应力σl作用,地层发生褶皱弯曲变形。背斜核部顶层的岩体位于单向拉伸区,局部应力场为单向拉应力状态σ;背斜核部底层岩体位于压剪区,局部应力场为压剪复合应力状态。文中研究对象限于背斜核部顶层岩体,即单向拉伸区。由于地层厚度h远小于地球半径R,可假定:①在顶层厚度h范围内,拉应力σ沿x轴均匀分布,顶层岩体受拉应力σ作用衍生拉裂纹;② 岩层在沉积过程中受环境、气候、物质组分等不均匀性因素影响,在一些薄弱部位发育拉裂纹,且沿岩层径向(x轴向)呈断续分布形态,沿岩层环向(y轴向)近似对称排布,具有断续周期裂纹特征。
在图2(a)中用虚线框沿径向x轴获取一列断续周期裂纹,经逆时针旋转90°,进一步概化为断续周期裂纹力学模型,如图2(b)。裂纹出现周期为2b,相邻裂纹之间岩桥长度为2(b-a),所受单向拉伸应力与图2(a)中局部单向拉应力σ相等。
在图2(b)中通过虚线框获取中心裂纹力学模型〔图2(c)〕,分析两侧裂纹对中心裂纹断裂扩展的影响。其中o1o2为中心裂纹,o1N和o2M为岩桥半长b-a,中心裂纹力学模型(基本单元)所受单向拉应力与图2(b)中所受单向拉应力σ相等。
图2(c)中的中心裂纹是图2(b)中断续周期裂纹的一个基本单元,而图2(b)中断续周期裂纹是图2(a)背斜核部地层的一列子单元。因此,通过分析中心裂纹基本单元的断裂问题,可以反映背斜核部断续周期裂纹的宏观断裂破坏特征,而线场分析法是分析中心裂纹模型的实用力学方法,经优化后的线场分析法可以更好地应用于该类地质模型分析中。

图2 中心裂纹模型概化流程Fig. 2 Simplified flowsheet of the central crack model
对于单向拉应力σ作用下的含中心裂纹岩体,将垂直于裂纹面o1o2方向、位于岩桥o1N和o2M上的岩桥内部拉应力σy进行修正,可得到既满足裂纹面应力边界条件的同时又满足岩桥上应力边界条件的解答。因此,按照线场分析法的力学思路,中心裂纹问题的重点转化为求取修正系数。
线场分析法的目标是求得应力强度因子,如式(1):
(1)

2 岩体断裂特征参数
2.1 岩桥应力修正值与静力平衡因子拆分
2.1.1 岩桥应力修正值
图2(c)为单向拉伸下含中心裂纹岩体,直角坐标系xoy的原点建立在裂纹面中心点o处,x轴重合于裂纹面,y轴垂直于裂纹面。o1o2为裂纹长度为2a的裂纹面,岩体宽度为2b,M、N为岩桥与两侧自由边的交点。
既满足图2(c)中裂纹面应力边界条件,又满足岩桥应力边界条件的拉应力场为:
(2)
式中:σy为岩桥上的拉应力,kPa;T为应力修正值,kPa,是关于外荷载σ、岩体宽度2b及裂纹长度2a的函数。
沿MN切割形成A、B两个区域。由于岩桥几何尺寸相对侧自由边尺寸很小,属于小边界问题,可以按照圣维南原理对A区域建立沿y方向的静力平衡方程:

(3)
将式(2)代入式(3),由于应力修正值T与积分变量r无关,从积分式中提取得:
(4)
将式(4)代入式(2)即可得岩桥上的拉应力σy,再将拉应力σy代入式(1),即求得应力强度因子KI。
2.1.2 岩桥静力平衡因子拆分
求解应力修正值T的关键是求解式(4)中分母的定积分式,即:
(5)
式(4)的分母〔式(5)〕是求解静力平衡方程式(3)的桥梁,故将式(5)左侧命名为“岩桥静力平衡因子”。为将岩桥静力平衡因子的定积分求解问题一般化,可暂不讨论积分区间,将式(5)转化为不定积分式,如式(6):
(6)
式中:被积函数的分子为关于矢径r的一次多项式,可将其拆分为两个不定积分式的线性组合:
(7)
(8)
式中:A0(r)表示不定积分中被积函数分子r的幂次为0,下文统称零次幂积分因子;A1(r)表示不定积分中被积函数分子r的幂次为1,下文统称一次幂积分因子。
对积分因子A0(r)和A1(r)进行线性组合,得到不定积分式B(r),再给出相应的积分区间,即可得到岩桥静力平衡因子〔式(5)〕。
2.2 岩体断裂特征参数求解
2.2.1 积分因子求解
为了分析系统(9)—(10)的稳定性,首先由投影算子的非扩张性及常微分方程解的可延拓性,得到如下引理。
1)零次幂积分因子A0(r)
根据线性换元法和三角换元法,式(7)的解为:
(9)
2)一次幂积分因子A1(r)
与推求A0(r)相似,通过线性、三角换元法可得:
(10)
由积分公式结论[21]有:

(11)
当式(11)中j=2时,式(11)即为式(10),可得:
(12)
通过线性、三角换元反解,式(12)化为:
(13)
由式(13)可得,当r=0时,A1(0)=C2,积分因子的线性组合如式(14):
(14)
2.2.2 岩桥静力平衡因子线性组合求解
(15)

(16)
2.2.3 岩桥应力修正值及拉应力求解
将式(16)代入式(4)可得岩桥应力修正值,如式(17):
(17)
将式(17)代入式(2)可得岩桥拉应力,如式(18):
(18)
2.2.4 应力强度因子及形状修正系数求解
将式(18)代入式(1),得到裂纹面两端应力强度因子,如式(19):
(19)
由式(19)可知,有限宽岩体较无限大岩体应力强度因子多一个修正系数F,如式(20):
(20)

3 结果分析与讨论
3.1 形状修正系数F变化规律
将图2(c)中裂纹长度2a与岩体宽度2b的比值视为裂纹贯通率n,即n=a/b(0≤n≤1)。当n=0时,表示完整岩石;当n=1时,表示岩体已经破坏。
由式(16)和式(20)可知,形状修正系数F是关于裂纹贯通率n的一元非线性函数,F随着裂纹贯通率n变化而变化。为了考察形状修正系数F函数的形态,通过文献[13]、文献[16]和文献[22],结合式(20),获得了形状修正系数对数值lg(F)分布,如图3。

图3 形状修正系数对数值lg(F)分布Fig. 3 Distribution of shape correction coefficient lg(F)
由图3可知:
1) 修正系数对数值lg(F)均随着裂纹贯通率n的增加呈非线性单调上升趋势,文献[22]的裂纹贯通率n>0.8后形状修正系数的增长速度低于其它3种的情况除外。随裂纹贯通率n增加,形状修正系数F总体上对裂纹尖端应力强度因子的调增作用越大。形状修正系数大致分为三段式增长区间:裂纹贯通率n<0.3区间为慢速增长阶段;裂纹贯通率n处于0.3~0.6区间为中速增长阶段;裂纹贯通率n>0.6 区间属于快速增长阶段。
2) 当裂纹贯通率n→0时,F→1,式(19)退化为无限边界中心裂纹尖端应力强度因子解;当裂纹贯通率n→1时,除文献[22]外,其余曲线的形状修正系数F→+∞,因为该条件下,其余曲线公式的分母趋近于0,而文献[22]对应的Isida公式的最小二乘法是关于裂纹贯通率n的有限多项式,在数学上是有界的。实际上,当裂纹贯通率n→1时,即裂纹长度2a趋近于岩体宽度2b时,岩体接近破坏,在此种条件下,即便外部荷载不增加,但是受形状修正系数的调整,应力强度因子将快速突破断裂韧度,材料发生破坏。由此可知,文献[22]中Isida公式的最小二乘法在裂纹贯通率n→1时不合理。
3) 文献[16]裂纹共线等距等长解是断裂力学中将无限边界体结果推广到有限宽度板条的经典解法,具有较高的精度,但是这种解法仍然是一种近似解;文献[22]中Isida公式的最小二乘法是基于试验统计数据,其为采用统计分析方法拟合的多项式公式,具有一定的统计意义,但也是一种近似解法;文献[13]根据线场上静力平衡方程得出的公式具有严格的力学逻辑,但其基于圣维南原理的积分因子,难以精确满足线场上的应力边界条件,而只是通过积分方式近似满足其应力边界条件,同时对积分因子进行整体积分具有相对复杂的数学技巧;文中解基于线场上的静力平衡方程,采用拆分与组合方法进行改进,更方便快捷,也是合理可信的。
3.2 应力修正值T变化规律
联立式(16)、式(17),可得应力修正值T关于裂纹贯通率n和外荷载F(F=σ)的表达式(21),并绘制函数曲线(图4)。
(21)

图4 应力修正值T函数曲线分布Fig. 4 Distribution of stress modified value T function curve
由式(21)和图4可见:当外荷载不变,应力修正值T随着裂纹贯通率n的增加呈非线性增加趋势;当裂纹贯通率n不变,应力修正值T随着外荷载的增加呈线性增加趋势;当裂纹贯通率n→0时,式(21)无意义,即式(21)仅适用于带裂纹岩体;当裂纹贯通率n→1时,应力修正值T→+∞,即岩桥上拉应力无穷大,岩体已经破坏。
4 算例分析
4.1 岩体抗拉强度对比

(22)
利用式(16),结合K准则判据,可得岩体抗拉强度如式(23):
(23)
根据式(23),获得灰岩岩体抗拉强度为0.337 MPa。按照文献[22]和文献[13]中的应力强度因子公式推导出岩体抗拉强度公式而获得的灰岩岩体抗拉强度值见表1。由表1可知,4种解法所得岩体抗拉强度值介于0.325~0.341 MPa,平均值为0.334 MPa,标准差为0.007 MPa,变异系数为0.02,表明文中的解是合理的。

表1 岩体抗拉强度分布Table 1 Distribution table of rock mass tensile strength
4.2 基于文中解的岩体抗拉强度变化规律
裂纹贯通率n和裂纹半长a是影响岩体抗拉强度值的几何特征指标。在式(23)中取裂纹半长a为0.2~2 m的数值,裂纹贯通率n为介于0~1之间的变量,据此绘制在不同裂纹半长a下的岩体抗拉强度关系曲线(图5)。
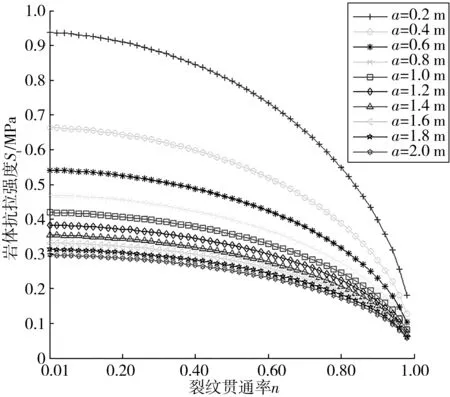
图5 岩体抗拉强度随裂纹特征的变化规律Fig. 5 Variation law of rock mass tensile strength changing with crack characteristics
由图5可见:
1)裂纹半长a一定时,岩体抗拉强度St随裂纹贯通率n增大而降低;裂纹半长a介于0.2~0.8 m且裂纹贯通率n<0.6时,岩体抗拉强度值较大;裂纹半长a>0.8 m时,岩体抗拉强度随裂纹贯通率n的增加,趋于平缓。
2)裂纹贯通率n一定时,岩体抗拉强度St随着裂纹半长a增加而降低(St与a的二次根式成反比)。
3)裂纹贯通率n一定且0.2 m≤a≤1.0 m时,岩体抗拉强度St变幅较大;1.0 m 4)0.2 m≤a≤2.0 m时,灰岩岩体的抗拉强度均未超过1.0 MPa。 将背斜核部岩体拉裂纹的发育和断裂问题概化为中心对称拉伸断裂破坏模型,引入经优化的线场分析法使中心裂纹模型计算过程方便快捷,物理概念清晰。岩桥静力平衡因子是求解岩体断裂特征参数如岩桥应力修正值、岩桥拉应力、应力强度因子及形状修正系数的关键,并得出了中心对称裂纹岩体抗拉强度表达式。主要结论如下: 1)形状修正系数随裂纹贯通率增大呈非线性单调上升,表明裂纹贯通率越高,形状修正系数对裂纹尖端应力强度因子的调增作用越大;当裂纹贯通率趋近于0时,应力强度因子解退化为无限边界中心裂纹模型解;当裂纹贯通率趋近于1时,形状修正系数趋于无穷大,岩体破坏。 2)当外荷载不变,应力修正值随裂纹贯通率增大呈非线性增加趋势;当裂纹贯通率不变,应力修正值随外荷载增大呈线性增加趋势;当裂纹贯通率趋于0时,文中解无意义,即仅适用于带裂纹岩体;当裂纹贯通率趋于1时,应力修正值趋于无穷大,即岩桥上拉应力无穷大,岩体破坏。 3)获得了中心对称裂纹岩体的抗拉强度表达式。以灰岩为例,计算对比发现:4种理论解法(含文中解)所得岩体抗拉强度值介于0.325~0.341 MPa,平均值为0.334 MPa,标准差为0.007 MPa,变异系数为0.02,表明文中解是合理的。裂纹半长一定时,岩体抗拉强度随裂纹贯通率增大而降低;裂纹贯通率一定时,岩体抗拉强度随裂纹半长增加而降低;岩体抗拉强度与裂纹半长的平方根成反比,表现出岩体抗拉强度变幅随裂纹半长线性变化而呈非线性变化的规律;裂纹半长介于0.2~2.0 m时,灰岩岩体的抗拉强度均未超过1.0 MPa。5 结 论
