静电喷雾沉积半径的预测模型
2022-06-24于涵王宏朱恂丁玉栋陈蓉廖强
于涵,王宏,朱恂,丁玉栋,陈蓉,廖强
(1 重庆大学低品位能源利用技术及系统教育部重点实验室,重庆 400030;2 重庆大学工程热物理研究所,重庆 400030)
随着现代工业的不断发展,高质量的薄膜和涂层显得越来越重要。以有机光伏电池(OPV)为例,优秀的电极薄膜能够极大地提升光电转换效率。大多数有机材料可以使用浸涂法、丝网印刷法和旋涂法进行制备,而上述方法会造成基底腐蚀,这使得利用上述方法制备由不同聚合物形成的多层结构变得困难。电喷雾沉积由于其独特的电流体力学机理而引人注目。与化学或物理气相沉积方法相比,电喷雾不仅具有更简单的结构和更好的可扩展性,而且相比旋涂方法具有更高的材料利用率。
电喷雾是一种通过高压电使液体雾化的方法。电喷雾具有多种喷雾模式,如微滴、纺锤、锥形喷射和多喷射模式,具体取决于所施加的电压、流速、电极配置以及液体的物理特性(如电导率、黏度、表面张力和密度)。其中,锥-射流模式是指在电场的作用下,毛细管口处的球形液滴会被拉伸成锥形,尖端会发射出一条射流并在向下的飞行过程中分解成液滴。由于锥-射流模式下产生的液滴粒径非常小,且具有较高的均匀性,已经成为制造薄膜最有吸引力的方法。在有机发光二极管(OLED)和有机光电器件的制造中,部分学者将静电喷雾技术作为薄膜电子器件的沉积方法。这些研究表明,静电喷雾沉积的有机薄膜性能优良,对曲面基板的适应性较好;由于液滴和导电基板之间的库仑吸附力,材料的利用率可以高达100%。在燃料电池领域,研究者们将静电喷雾技术沉积了多孔涂层和催化剂,研究发现,基板上沉积的粒子可以造成局部电场畸变,使涂层上生长出微观的树突状(分支)结构,从而改善电池性能降低内阻并提高催化剂利用率。
然而,相比压力式喷雾,静电喷雾的沉积过程更加复杂,由于液滴受电场力、曳力、库仑力等的耦合作用,了解和控制静电喷雾的沉积特性一直是该技术的应用难点和研究热点。Gañán-Calvo等和Hartman等开发了数值程序以研究静电喷雾液滴的传输过程;Jung等采用了移动喷嘴,以提高喷雾液滴沉积的均匀性;Stevenin等通过数值仿真和试验,研究了空气流场对静电喷涂过程和沉积面积的影响。但是,现有的研究结论只能定性地给出相关规律,无法向实际中的工程案例给出建议。目前工业应用中静电喷雾的沉积面积仍然只能通过反复调试获得,如何快速地获取合理的静电喷雾操作参数成为静电喷雾技术应用和推广的瓶颈。没有科学准确的喷雾沉积面积及关于操作参数的预测模型,将不能保证生产过程的高效和产品质量的稳定。
本文首先基于高斯定律,推导了静电喷雾的等效空间电荷场,然后根据受力平衡方程导出了静电喷雾沿轴向距离上的扩展半径。随后对模型进行了验证,发现即使在较低的电场强度下,模型也能够非常准确地预测静电喷雾的轮廓和沉积面积。本工作对静电喷雾雾化器的设计、使用具有重要的理论指导意义。
1 建模与仿真方法
1.1 物理模型和假设
对静电喷雾进行建模之前,首先要对其物理过程进行分析。图1(a)给出了典型的双电极结构静电喷雾系统。其中,喷嘴连接一高压电源,顶部有工质输入;环形电极放置在喷嘴下方一定距离处并连接一高压电源。喷嘴与环形电极之间的高电场使流体弯月面形成稳定的泰勒锥;环形电极与地面建立的驱动电场使喷雾液滴向下飞行,最终沉积在地面电极上。另外,该结构下的静电喷雾系统对不同工况的适应性更高。需要调整喷雾的沉积图案时,可以通过同时调节两电极的加载电压、直接控制静电喷雾液滴所处的电场环境,而不改变喷涂模式。因此,为了提升静电喷雾喷射的稳定性,提高增加雾化操作的灵活性,本文选取三电极结构进行分析、设计和实验。根据本文中设计的实验结构参数,建立了图1(b)所示的二维轴对称计算模型。定义计算域环形电极下表面为=0 平面,垂直向下为轴正向,以环形电极圆心位置=0为原点,同时将该点设置为喷雾液滴的出口位置。模型中,喷嘴与环形电极的电势分别为与,且<,环形电极到地面的距离为。
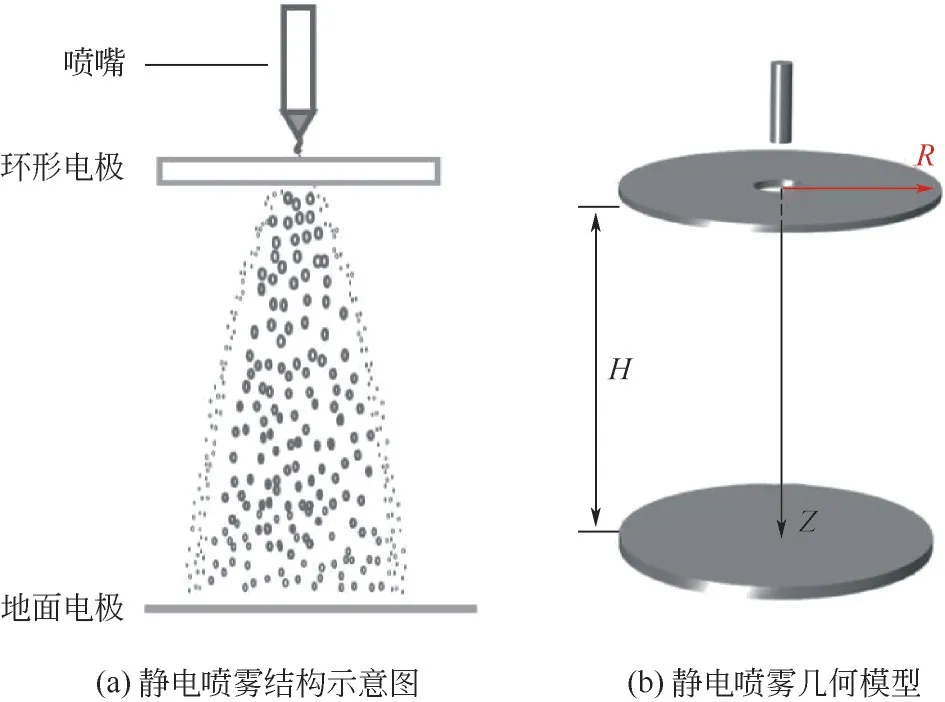
图1 静电喷雾的典型结构和几何模型
1.2 基于拉格朗日方法的液滴轨迹模型
拉格朗日液滴动力学仿真是基于Gañan-Calvo等提出的模型。模型将电喷雾液滴看作离散的粒子,对这些粒子而言,其动力学由牛顿第二定律描述,见式(1)。
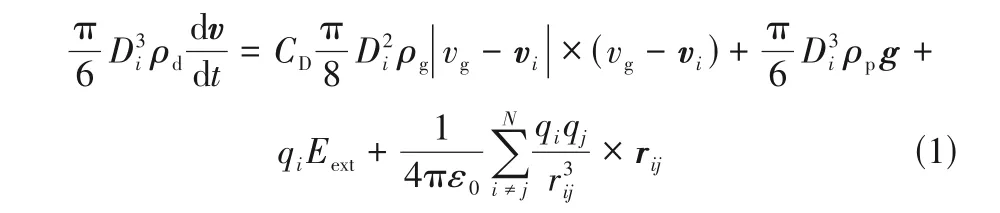
式中,右侧第一项为液滴受到的曳力,为阻力系数;为液滴直径,m;为密度,kg/m;v为第个液滴速度,m/s;为气流速度,m/s;右侧第二项为液滴受到的重力,为重力加速度,m/s;第三项为液滴受到的电场力,为液滴荷电量,C;为外部电场强度,V/m,可由高斯定律求解得到;右侧第四项为液滴之间的库仑作用力,r为第个液滴到第个液滴的距离,m;为真空介电常数,F/m;下角标和代表液滴编号;下角标p和g分别代表粒子和气体。根据Gañán-Calvo等提出的关联式,可计算出不同物性和工况下静电喷雾的平均粒径和平均荷电量,见式(2)~式(4)。
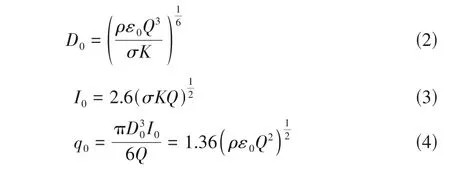
式中,为体积流量,m/s;为表面张力,N/m;为电导率,S/m;为静电喷雾电流,A。
由此,液滴的运动状况可由其位置矢量和速度矢量v描述,见式(5)。

1.3 静电喷雾轮廓模型
在库仑力的作用下,静电喷雾液滴相互排斥,这是静电喷雾羽流在径向上发生膨胀的根本原因。因此,液滴荷电量大小决定排斥作用是否强烈,液滴在空中的平均停留时间决定其横向迁移距离的大小。在喷雾液滴向下飞行的过程中,羽流最外侧液滴的受力情况和偏转距离往往决定喷雾的沉积直径,因此只需要观察喷雾边缘液滴的运动情况,即可得到大致的喷雾轮廓。然而,在同一时刻,静电喷雾是由无数个带电液滴组成的。如式(1)所示,观察其中某一液滴,它要受到所有其他液滴所施加的库仑力。正如“定律”所描述的,空间内粒子数量越多,需要计算的库仑力次数越多。因此要对模型进行简化,快速计算出液滴所受库仑力的合力。
为推导出静电喷雾的轮廓预测模型,即描述静电喷雾产生后在不同高度处的膨胀面积,需对静电喷雾的物理过程作一定简化。
(1)环形电极与地面为两个相互平行的导体,它们之间的电场可近似为均匀的电容器间的电场,可称之为“驱动电场”,。
(2)Deng等认为,液滴的运动状态由电场强度决定,轴向速度V几乎是恒定的(变化量<10%)。因此认为液滴在喷雾的轴线方向上受力平衡,电场力和曳力大小相等,符号相反。化简受力平衡方程得到,所受曳力按照简化的斯托克斯方程计算,π,其中为环境气体的动力黏度(Pa·s),联立两式即可得到液滴的轴向速度表达式:V=qE/(3π)。
(3)在喷雾液滴的飞行过程中,其直径会因为蒸发效应而不断减小,表面电荷密度不断增大。当液滴局部库仑力大于其表面张力时,将引起液滴的二次分裂。但在三电极结构下,液滴在环境中的飞行时间极短(仅为微秒级),因此忽略蒸发效应导致的库仑分裂,认为喷雾液滴到达地面时粒径、荷电量均保持不变。
(4)Tang等的研究结果表明,静电喷雾液丝的破碎过程中会产生卫星液滴。然而卫星液滴所占的喷雾流量仅为总流量的3%,对静电喷涂沉积均匀性的影响可忽略不计,因此模型中未作考虑。
1.3.1 静电喷雾的等效电荷法
推导过程中用到了等效电荷法,即将喷雾流场内的所有带电液滴看作一个整体,利用高斯定律将静电喷雾等效为空间电荷场,那么带电液滴在喷雾附近任意位置受到的其他液滴库仑力的合力,就等于该液滴在电喷雾等效电场中受到的电场力。如图2所示,以喷雾出口为原点,建立二维轴对称坐标系,沿喷雾轴线向下为轴,沿喷雾径向为轴。沿着轴方向取一控制体,控制体顶部面积为、底部面积为、侧面积为、沿轴方向上的厚度为δ。
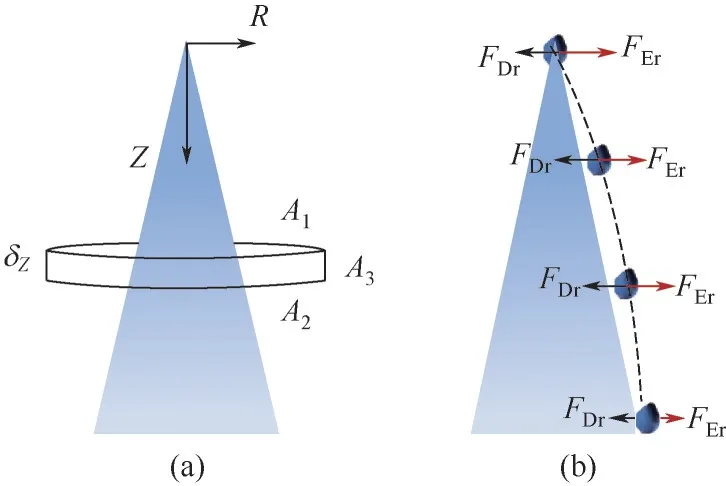
图2 静电喷雾的液滴受力分析和控制体积
对控制体应用高斯定律,有式(6)。
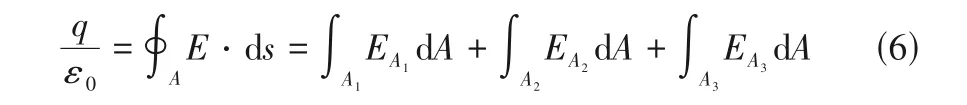
式(6)的含义为控制体包含的电荷量与真空介电常数的比值等于穿过控制体各表面的电场强度通量之和。其中,为控制体包含的电荷量(C),其值与静电喷雾的电流有关,见式(7)。

式中,V为液滴在控制体位置处的轴向速度,m/s。由于控制体的上下端面相互平行,因此电场强度大小相等,符号相反(E=-E)。当控制体厚度δ无限小时,,2πrδ,因此式(7)可写成式(8)的形式。
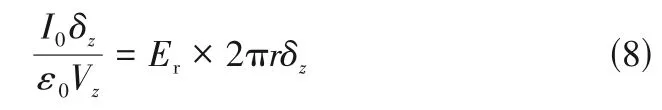
移项可得静电喷雾的等效空间电荷场,见式(9)。

1.3.2 单喷雾的羽流和沉积半径
得到了静电喷雾的等效空间电荷场,下面只需对液滴的最大偏转距离进行分析。如图2所示,在轴方向上,液滴主要受到喷雾等效电荷场施加的电场力和曳力。值得注意的是,喷雾液滴沿径向飞行过程中,受到的合力是不为零且动态变化的,因此对液滴运动情况的数学描述应使用二阶微分的加速度方程,见式(10)、式(11)。
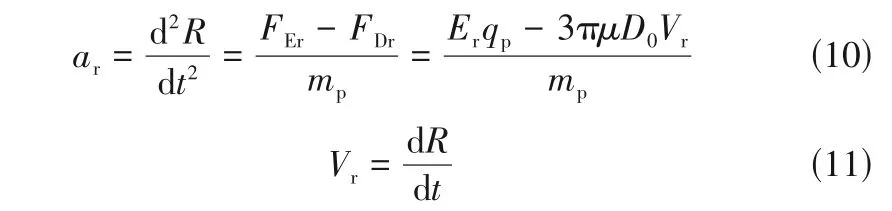
式中,为液滴在方向上的加速度,m/s;为主液滴荷电量,C;为主液滴质量,kg;为液滴的径向速度,数值上等于径向位移对时间的导数。将式(11)代入式(10)中移项得到式(12)。
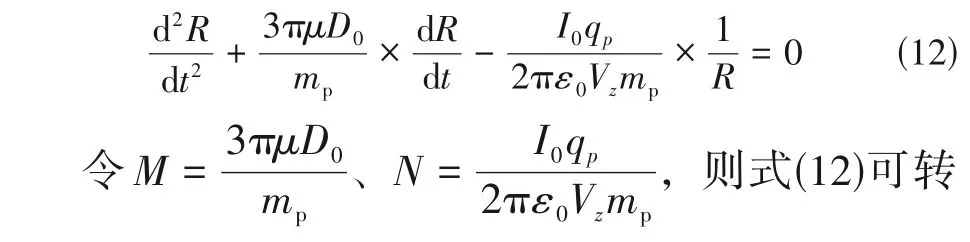
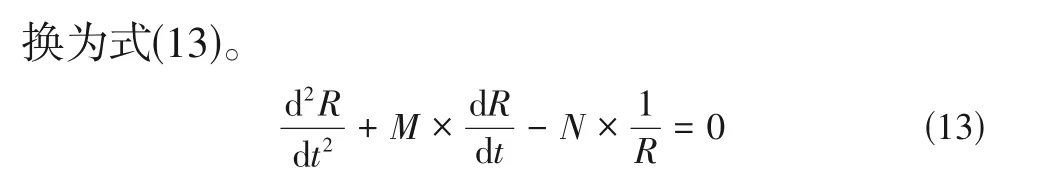
式(13)的初始条件为:=0时,=0、=0;=时,=、=。
此方程为二阶非线性微分方程,无法给出解析解,因此采用数值方法求解。
2 实验方法
图3显示了静电喷雾的可视化实验装置,它由喷嘴、环形电极和基板组成。喷嘴选用内径ID=1mm,外径OD=1.2mm的不锈钢管,环形电极位于喷嘴下方约1mm 处。环形电极孔径为2mm,并与喷嘴出口同心。基板下方为手动升降台,可调整环形电极-地面间距为10~30mm。喷嘴入口连接一微量注射泵(型号:LSP01-2A,兰格恒流泵有限公司)为静电喷雾提供流量。选用天津东文高压公司生产的静电纺丝电源(型号:DW-P303-1ACH2、DW-N303-1ACH2)作为静电喷雾的动力来源,分别连接喷嘴和地面。其中,喷嘴接正电,基板接负电,环形电极接地。两台电源的输出电压范围为0~±30kV,调整精度1%。
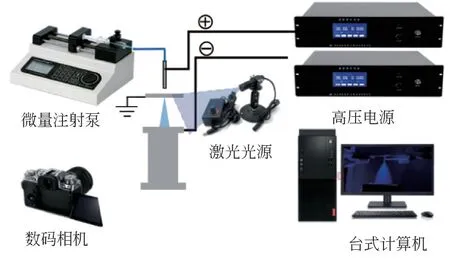
图3 静电喷雾可视化实验装置
实验中在喷雾一侧布置一台高速数码相机[型号:FUJIFILM XT-4,富士胶片(中国)投资有限公司;镜头:尼康PC-E 85mm f/2.8D移轴定焦镜头]。因为喷雾液滴的尺寸较小且飞行速度较快,常规的打光方式无法显示清晰的喷雾轮廓,因此在相机对侧布置一台激光器(深圳市红外线激光科技有限公司,HW450AL500-16GD,450nm)作为辅助光源。为了得到喷雾轮廓图像,实验中采用相对较长的曝光时间以追踪液滴轨迹。实验中使用的工质是无水乙醇,其物性参数如表1所示。实验后使用ImageJ软件可精确测量不同工况下的沉积半径。

表1 无水乙醇的物性参数(25℃)
3 结果与讨论
3.1 电场强度的影响
为了探究电场强度对喷雾轮廓和沉积面积的影响,并验证预测模型的准确性,本文对Oh 等的工作进行了数值模拟。根据该文献中的实验台结构,在数值模拟中选定针管外径OD=1.58mm,针管-环形电极间距=3mm,环形电极上孔径3mm,距接地电极=30mm。其中,针管施加电势,环形电极接地=0V,基板施加电势。主液滴粒径服从正态分布,标准差/9,不考虑卫星液滴带来的影响。
图4 显示了来自数值模拟[式(5)]计算出的二维坐标系下液滴位置分布及预测模型[式(13)]导出的轮廓曲线。由于实际结果中液滴过于密集,图4中有部分喷雾内部液滴被省略。如图4 所示,由式(13)计算出的曲线准确地贴合在喷雾羽流外侧,描述了静电喷雾的膨胀趋势。从图4(a)看出,当电场强度较低时,环形电极小孔附近的喷雾液滴非常密集,导致此处的电荷密度非常大,喷雾径向扩张迅速。式(13)能够精准地捕捉到此过程。
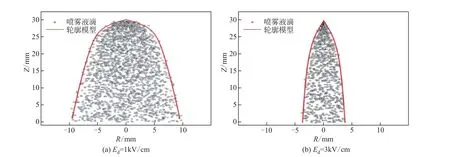
图4 静电喷雾数值模拟与轮廓模型对比
图5显示了相同结构下,不同电场强度时的喷雾沉积半径。如图所示,喷雾轮廓模型与数值模拟结果非常吻合,且随着驱动电场强度的不断提升,吻合程度不断提高。在电场强度较低(=1kV/cm)时,预测模型得到的沉积半径略高于Oh 等得到的结果,误差约为7.41%。这是因为喷雾入口处液滴依次产生且数量稀少,空间电荷密度较低,造成液滴发生偏转的库仑力十分微弱。而等效电荷法则会高估附近电场强度,使喷雾液滴偏转程度增大。电场强度增加后,预测值将略小于模拟值,这是因为轮廓模型中的“恒定速度假设”忽略了液滴在毛细管口的加速阶段,使其平均轴向速度被高估,在板间的飞行时间缩短,液滴未经充分偏转就已经到达地面。该假设造成的影响会随着驱动电场强度的增大而逐渐消失,因为更大的电场强度可以为液滴提供更大的轴向加速度,使其更快地到达假设中的“恒定速度”。
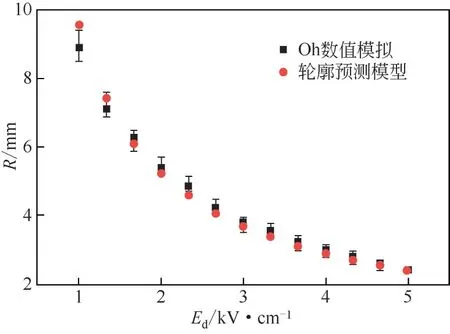
图5 数值模拟与喷雾轮廓模型给出的沉积半径比较
3.2 喷雾流量的影响
为了更清楚地捕捉喷雾轮廓,提升拍摄质量,设置环形电极到地面的距离=20mm,定量研究了在不同电场强度下三种流速(1mL/h、2mL/h 和3mL/h)的喷雾轮廓模型的喷雾轮廓和沉积半径。如图6所示,喷雾流量提升后,喷雾的沉积面积增大。选取工程中常用的电场强度范围;图7显示了实验与预测模型得到的喷雾沉积半径。与前文得到的结论一致,随着电场强度的增大,喷雾的沉积面积逐渐减小。轮廓预测模型[式(13)]得到的结果略小于实验结果,且随着电场强度的增大误差逐渐减小。值得注意的是,当喷雾流量较大时,预测模型与真实值之间的误差会相对增大(=1mL/h时=7.45%,=3mL/h 时=10.1%)。造成此现象的原因是流量增大后,喷雾电流和液滴荷电量随之提升,式(9)计算得到的等效电荷场将略高于真实情况,导致液滴偏转更加剧烈。另外,流量增大后,喷雾羽流外侧包裹着一层卫星液滴,实验后提取喷雾底端轮廓时较为困难。

图6 不同流量下的喷雾轮廓
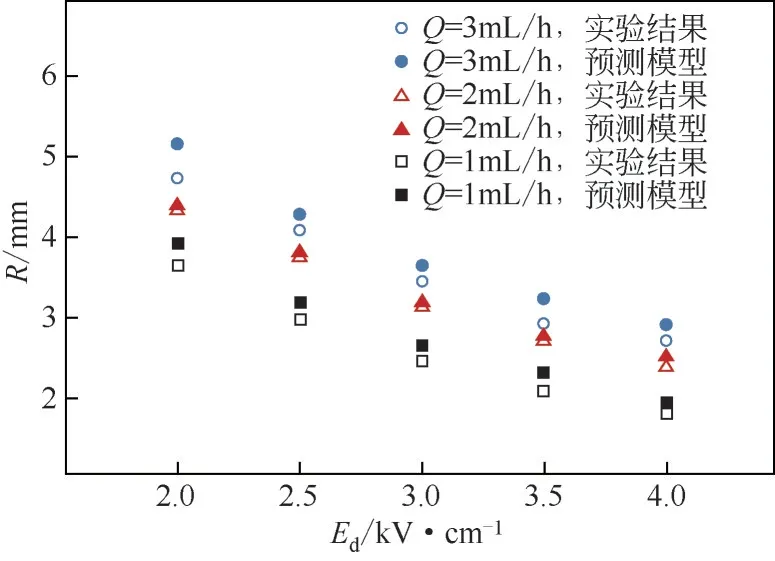
图7 实验结果与预测模型获得的喷雾沉积半径对比
4 总结
本文首先基于高斯定律,推导了锥-射流模式下的等效空间电荷场,随后根据静电雾化的原理和特性,从喷雾羽流的扩散机理出发,通过简化标准液滴的受力平衡方程,得到了用于预测静电喷雾扩展半径的数学模型。
(1)静电喷雾的沉积面积受多种因素影响,仅考虑喷雾外侧液滴的偏转距离可以简化计算过程并有效预测扩展半径。与文献和实验中的结果进行对比,该模型可以较好地反映静电喷雾在不同位置处的扩展半径,最大偏差为10.1%。
(2)增大电场强度后喷雾沉积半径减小,液滴覆盖区域更加集中;增大流量后喷雾沉积半径增大,实验中可明显观察到羽流外侧存在卫星液滴。
(3)对模型的二阶非线性方程组采用数值求解,获得喷雾轮廓的耗时仅为分钟级,与计算流体动力学(CFD)中拉格朗日方法相比极大缩短了求解时间。该模型可为工程应用中快速地计算喷雾覆盖面积提供指导。
