阴阳对优化算法在旅行商问题中的推广与应用

樊志领，郭东威，陈 娜，刘 伟

(周口师范学院 数学与统计学院，河南 周口 466001)

阴阳对优化算法(Yin-Yang-pair optimization, YYPO)是由Varun Punnathana等人于 2016 年提出的一种用于求解连续型单目标优化问题的元启发式优化算法[1]。YYPO算法的灵感来自于宇宙中广泛存在的对偶关系，如男和女、光明与黑暗、正负电荷、波粒二象性、二进制中的0和1等。这种对偶关系在中国古典著作《易经》中被称为阴和阳，阴和阳两种状态在保持着对偶关系的同时，还会在一定条件和程度下相互依存与转化。YYPO算法受到这种对偶关系的启发，寻求搜索空间中的全局探索和局部开发之间的平衡状态，实现对复杂优化问题的解空间的高效搜索。

旅行售货员问题(Travelling Salesman Problem, TSP)是图论中一个经典的组合优化问题，也是一个典型的NP-完全问题(NP-complete problem, NPC)，其目标是在一个赋权图中找一条遍历所有节点并回到出发点的最短路线[2-3]。按照权重和旅行线路的多少，TSP问题可分为对称TSP问题、非对称TSP问题、多TSP问题三类，目前这三类问题均有不同的求解方法[4]。在一个节点数为n的赋权完全图中，TSP问题可行解的数量是(n-1)!，当网络中节点数量较多时，求TSP问题的精确解通常是困难的。因此，如遗传算法(Genetic Algorithm, GA)、分布估计算法(Estimation of Distribution Algorithm, EDA)、阴阳算法(Yin-Yang Algorithm , YYA)等优化算法常被用来求TSP问题的近似最优解。

GA算法是由美国的Holland于20世纪70年代提出的一种优化算法，该算法模拟了生物进化论中的自然进化过程，通过选择、交叉、变异三个算子和迭代的方式求解优化问题[5-6]。目前，GA算法被广泛应用于TSP问题、路径规划问题、生产调度问题等组合优化问题。张群等[7]通过改进的模糊逻辑控制器实现交叉概率和变异概率的动态调整，提高了GA算法求解混合车辆路径问题的收敛速度。郭东威等[8]提出了易位组合交叉算子、单车路径重排策略及需求对换策略，提高GA算法的寻优性能，有效求解了400个客户点的PDPTW国际算例集。

EDA算法的概念最早在1996年被提出，该算法通过统计学习的手段建立解空间内个体的概率分布模型，然后利用概率模型产生新的种群，通过迭代实现种群的优化[9-10]。Peter A N和Bosman等[11]研究了将EDA算法从离散型问题推广到连续型问题，同时保持算法性能的方法。Dirk Sudholt等[12]从EDA算法中的更新强度入手，通过对算法步长的研究，提出了在全局优化中设置更新强度的新准则。

YYA算法是由Tam S C等人结合中国古典著作《易经》中的阴和阳的概念，于2011年提出的一种专门用来求解TSP问题的算法，该算法利用《易经》中卦象之间的复卦、综卦和交互卦等三种转化方式，设计了变异、翻转和交互三个算子求解TSP问题[13]。值得说明的是，YYA算法与YYPO算法仅仅在名称方面有相似之处，在算法流程及操作过程中并没有类似之处[1]。

目前，YYPO算法主要被应用于求解连续型变量的优化问题，而TSP问题是一个离散型优化问题。本文针对YYPO算法和TSP问题的特点，将YYPO算法推广到TSP问题这一典型的离散型优化问题的求解中，设计出了一种离散型阴阳对优化算法(Discrete Yin-Yang-pair optimization, DYYPO)，并将该算法的求解结果与GA算法、EDA算法、YYA算法的求解结果相比较。结果表明，DYYPO算法在求解TSP问题时，比GA算法、EDA算法、YYA算法更有效。

1 YYPO算法

YYPO算法对所有的变量都作归一化处理，将其映射到从0到1的实数区间内，在迭代过程中通过分裂和存档两个阶段，利用P1点(开发点)和P2点(探索点)的择优交换实现种群的寻优过程。在YYPO算法中，P1的主要任务是开发，即开发可能出现最优解的潜在区域，获得更好的解；P2的主要任务是搜索，即扩大算法的搜索范围，寻找可能出现最优解的潜在区域。开发点P1和搜索点P2分别是以δ1和δ2为半径的超球体的中心，在算法的迭代过程中，以超球体的中心和半径随机生成新的附加点，且P1和P2会以一定的条件互换，以实现开发和探索之间的平衡。YYPO算法的迭代过程分为分裂和存档两个阶段，超球体的半径δ1和δ2受缩放因子α的控制分别具有增加和减小的趋势，确保了算法的收敛性。

1.1 参数初始化

1.2 分裂阶段

在分裂阶段，将P1和P2的相同副本保存为S，S的更新方式有单路分裂和D路分裂两种方式，这两种方式在迭代过程中会以同样的概率被随机选择。单路分裂更新公式为

式中的上标为变量序号；下标为点序号；r为0到1之间的随机数；δ为搜索半径。

D路分裂更新公式为

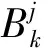
1.3 存档阶段

在存档阶段，首先比较P1和P2的适应值，若P2的适应值优于P1，则将P1和P2，δ1和δ2的值互换。然后根据存档次数I的取值范围[Imin,Imax]随机生成I的值，根据分裂阶段得到的结果进行存档，若存储的最佳点P0比P1和P2的适应值更好，则将P0与P1和P2交换。存档结束后，根据如下公式更新搜索半径δ1和δ2

式中δ1和δ2分别为P1和P2的搜索半径，α为缩放因子。

由上式可知，随着迭代的进行，δ1和δ2会分别呈下降和增长趋势，其中δ1的下降会保证算法的收敛。由于δ2随着迭代的进行呈增长趋势，因此须将δ2的最大值进行限定，通常取最大值为0.75。YYPO算法的详细过程可参考文献[1]。

2 TSP问题

TSP问题是指一名售货员从初始节点出发，经过其他所有节点，以最短的路径返回出发点的问题，该问题是一个非常著名的离散型的组合优化问题。TSP问题研究历史十分悠久，最早的研究开始于1759年，著名数学家Euler提出的在国际象棋棋盘上的骑士环游问题，Menger于1930年提出了TSP问题的一般数学模型，1954年Danzig等人利用割平面法解决了一个49个城市的巡回问题。TSP问题的数学模型为

对于节点数较少的TSP问题，可以通过线性规划方法或者穷举法求得问题的最优解。但由于TSP问题是一个NPC问题，当节点数超过100时，可行解的个数将超过10 150，此时利用穷举法求解该问题是不可能的。近年来，受蚂蚁、蜜蜂、鸟类、鱼群等生物种群活动影响的优化算法已经非常常见，这类算法虽然不能保证求得问题的理论最优解，但可以在理想的时间内得到近似最优解，利用这类算法求解TSP问题的近似解也已经成为了一个重要的研究方向。

3 利用DYYPO算法求解TSP问题

3.1 YYPO算法在TSP问题中的推广

一般情况下，利用优化算法求解n个节点的TSP问题时，可行解可以认为是由正整数1,2,…,n构成的一个随机排列的字符串。同时，由YYPO算法的分裂公式和存档阶段中开发半径、探索半径的更新公式可知，该算法主要用于求解连续型变量的问题，若将YYPO算法直接用于TSP问题的求解，可能会导致迭代过程中出现大量的非可行解。因此，现阶段对YYPO算法的研究无法直接用于TSP问题的求解。

本文结合YYA算法中的交互算子，利用YYPO算法的思想，将YYPO算法中的分裂过程、存档过程、求解过程中保持开发与探索之间的平衡关系和利用缩放因子控制开发半径和探索半径的方法应用到了TSP问题的求解中，设计出了一种求解TSP问题的DYYPO算法。

3.1.1 参数初始化

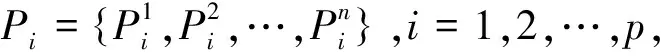
3.1.2 分裂阶段

(1)

图1 DYYPO算法的分裂阶段示意图

3.1.3交互阶段

交互阶段的主要任务是根据开发半径δ1或者探索半径δ2的值，生成一个二进制向量Bj，具体公式为

(2)

式中的r为0到1之间的随机数。然后利用Bj分别以0.5的概率对一个可行解执行下列两种交互操作的一种：

(1)将可行解中与Bj中字符0对应位置的节点放到新的可行解的前面，而将可行解中与Bj中字符1对应位置的节点放到新的可行解的后面；

(2)将可行解中与Bj中字符1对应位置的节点放到新的可行解的前面，而将可行解中与Bj中字符0对应位置的节点放到新的可行解的后面。

与分裂阶段相同，利用上述交互操作可以根据开发半径δ1或者探索半径δ2分别生成p个开发点和p个探索点。交互阶段的操作如图2所示。

图2 DYYPO算法的交互阶段示意图

3.1.4 存档阶段

在存档阶段，首先利用缩放因子α更新开发半径δ1和探索半径δ2的值，其公式为

(3)

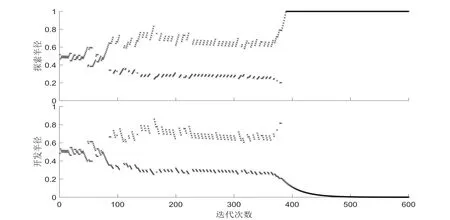
在分裂阶段和交互阶段，利用当前种群一共生成了2p个开发点和2p个探索点，可计算出开发点的最优值p1和探索点的最优值p2，将其中的最优值存储到新的种群中。然后比较p1和p2的大小。如果p2

DYYPO算法描述:STEP1 初始化,生成规模为p的初始种群和α,δ1,δ2等参数;STEP2 分裂阶段,根据公式(1)计算翻转字符串的长度,随机生成翻转字符串的起点,执行翻转操作,生成p个开发点和p个探索点;STEP3 交互阶段,根据公式(2)生成二进制向量Bj,执行交互操作,生成p个开发点和p个探索点;STEP4 存档阶段,根据公式(3)生成新的δ1和δ2,计算开发点最优值p1和探索点最优值p2,比较二者大小,判断是否将p1与p2、δ1与δ2的值交换,并将最优值存储到新种群中;STEP5 选取种群中适应值最好的p个点,作为下次迭代的初始种群;STEP6 判断是否达到最大迭代次数?若是,则转STEP7;若否,转STEP2;STEP7 将种群中的最优值作为求解结果输出,迭代结束。

在DYYPO算法的迭代过程中，初始种群的规模为p，分裂阶段和交互阶段分别产生了2p个新个体，加上最优值会被存储到新种群中，迭代产生的新种群规模为5p+1。在算法执行过程中，开发半径呈递减趋势，且每次迭代的最优解始终保留在新的种群中，因此DYYPO算法具有收敛性。

3.2 DYYPO算法求解TSP问题的具体过程

在本文中，选取的TSP问题算例均来自于国际标准测试库TSPLIB。首先选取TSPLIB中一个节点数为29个的算例Bays29，该算例的理论最优解的值为2020，利用DYYPO算法求解该问的具体情况如表1所示(运行环境：Intel core 2 Duo CPU 2.93Hz；2G RAM；MATLAB 2016b，下文同)。

从表1中的结果可知，在种群规模为200，迭代次数为600时，DYYPO算法运行100次就能够求得该问题的理论最优解，且求解结果的平均值与理论最优解较为接近，误差平均值为1.93%。在迭代过程中，开发半径δ1、探索半径δ2的变化情况和种群最优值的变化情况分别如图3和图4所示。

表1 DYYPO算法求解算例Bays29的结果

图3 开发半径与探索半径的变化情况

图4 种群最优值的变化情况

由图3可知，迭代次数在400次之前时，开发半径δ1和探索半径δ2的互换较为频繁，这意味着在该阶段探索点比开发点获得了更优的值，探索点的搜索在该阶段占主导地位。随后，开发半径δ1和探索半径δ2的互换逐渐减少，并分别收敛于0和1，且种群的最优值也呈现出收敛趋势，在经过大约500次迭代后逐步趋于稳定。同时，将图3和图4对比可知，无论开发半径δ1和探索半径δ2是否进行互换，均有可能出现适应值下降的现象，表明了开发点和探索点都能在一定程度上提高可行解的质量。

3.3 DYYPO算法与其他算法的对比研究

为了进一步测试DYYPO算法在求解TSP问题时的性能，选取了GA算法、EDA算法、YYA算法求解TSPLIB中的多个问题，并将求解结果与DYYPO算法的求解结果进行对比。本文选取TSPLIB中的10个节点数较少的算例对上述算法进行测试,为保证不同算法之间的可对比性，迭代过程中的种群规模p的值均取200，生成的新种群规模均为1001，循环次数均取1000次，所用到的算法主要流程如图5所示。

图5 本文用到的算法流程及种群规模示意图

利用上述算法求解所选取的节点数在29至225之间的10个TSP问题算例，每个算例中的节点个数均体现在算例名称中，每种算法均重复运行100次，求解结果见表2。

表2 利用不同算法求解TSP问题的结果

从求解的平均值及其误差方面来看，在所有选取的测试算例中，DYYPO算法求解结果的平均值均优于其他算法，这说明DYYPO算法在求解TSP问题时通常能获得相对较优的解。在最优值这一指标上，DYYPO算法在Bays29算例中求得了理论最优解；在Berlin52，Eil76和Ch130这三个算例中，DYYPO算法的结果要明显优于GA算法和YYA算法，但要稍劣于EDA算法；在其余6个算例中，DYYPO算法的求解结果均是最优的。

在平均用时这一指标上，DYYPO算法的用时比EDA算法和YYA算法要长，比GA算法要短。不同算法的用时随着节点数量的变化情况如图6所示，由图6可知，随着节点数量的增加，DYYPO算法用时的增长速度要明显低于其他算法，这一项数据表明DYYPO算法在用时方面较为稳定。将Bays29和Tsp225两个问题的用时情况进行对比，在节点数量增加了6.76倍的情况下，DYYPO算法的用时仅增长了1.14倍。相比之下，YYA算法的用时增长了1.78倍，比DYYPO算法略高，EDA算法和GA算法的用时均增加了8倍以上。因此，可以预测DYYPO算法在处理更大规模的TSP问题时会具有一定的时间优势。

图6 不同算法的用时随着节点数量的变化情况

4 结语

本文将求解连续型优化问题的YYPO算法推广到了TSP问题这一经典的离散型优化问题的求解中，利用YYPO算法中分裂操作和存档操作的思想，并结合YYA算法中的交互算子，设计了一种包含分裂、交互、存档等三个基本阶段的新的优化算法——DYYPO算法，并选取TSPLIB中的10个算例对算法性能进行测试。测试结果表明，与其他三种算法相比，DYYPO算法在求解的平均值、最优值和用时方面，均具有一定的优势。

需要说明的是，TSPLIB中算例的节点数量在十几个到上万个不等，本文选取的虽然是规模较小的算例，但DYYPO算法的求解时间已经很长。以Tsp225问题为例，算法的平均时间是24.86秒，若运行100次，总时间将超过40分钟。因此，如何利用DYYPO算法在较短的时间内求解更大规模的TSP问题，以及如何进一步提高求解的效率，是一个重要的后续研究方向。