土工织物反滤层对多孔管汇流量影响的试验研究

谢淑华，刘焕芳*，黄海涛，叶芳

(1.石河子大学水利建筑工程学院，新疆 石河子 832003；2.淮河水利委员会综合事业发展中心，安徽 蚌埠 233001)

随着全球气候变化及城市化的发展，出现了水资源短缺和部分地区地下水上升等问题，多孔管为摆脱这种困境提供了一种思路.含有反滤层的多孔管广泛应用于农业、水利、市政等领域，主要用于集水和排水[1-2].传统的反滤层滤料一般为砂砾石，但有些地区受砂砾石来源的限制，用土工织物代替砂砾石作为反滤层[3]，土工织物具有运输、施工方便，造价低，耐久性好，透水性好等特点.STUYT等[4]研究暗管排水外包滤料的设计，提出土工织物滤层的选择标准，从而推动了土工织物作为多孔管外包滤料的发展.SALEM等[5]研究发现，多孔管外包土工织物的厚度和特征孔径的大小对淤堵程度有影响.刘文龙等[6]结合实际工程并通过室内渗透试验研究了2种土工织物用于黄河三角洲土壤暗管排水外包滤料时的反滤效果以及防淤堵性能.除此之外，也有许多学者研究了土工织物反滤层的微观结构对其渗透性和防淤堵性能的影响[7-10].

汇流量是多孔管设计的重要技术指标，反滤层对多孔管汇流量具有重要的影响.针对含有反滤层的多孔管汇流量问题，国内外专家学者进行了大量研究，MURPHY等[11]利用能量方程和CFD模型，基于Kirkman理论给出了含土壤层的流量表达式.黄海涛等[12]在阿拉维娜-努美诺夫公式的基础上并结合室内试验建立不同来流流量下的渗管出水量的回归方程.郑晓瑜等[13]探究了砂石料反滤层厚度对多孔管的汇流量的影响.

随着含有土工织物反滤层多孔管的推广使用，对其汇流量的研究显得尤为重要.文中将在前人的研究基础上，通过理论分析和室内试验，研究土工织物反滤层厚度、面密度对多孔管汇流量的影响，以期为工程中含有土工织物反滤层的多孔管设计提供参考.

1 试验设计和方法

图1为试验装置示意图.本试验在长为11.0 m,宽为0.6 m，高为0.8 m的矩形断面渠道中进行.试验装置包括离心泵、高位水箱、多孔流体分布管和三角堰等.采用管径D为0.156 m的PVC圆管，管长L为4 m，管顶有3排孔，孔径d为0.02 m，孔距s为0.05 m，孔呈梅花状分布，管道始端用堵头封堵，管道外部用土工织物覆盖.将管道水平放置在渠道中间，使管道的坡度为0，在渠道尾部设有调节阀，用于控制渠道内水位，并将水位控制在0.1～0.6 m.

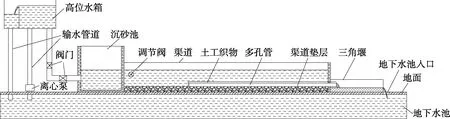
图1 试验装置示意图

试验开始时，打开进水阀，水流进入渠道内，再调节渠道的调节阀，使管顶初始水深为0.1～0.2 m，待水位平稳后，记录三角堰测针度数.再调节渠道的调节阀，使渠道内水位上涨0.03～0.07 m，水位平稳后，记录三角堰测针度数.重复以上试验，直至水位到达0.5 m时，结束本组试验.关闭进水阀，待渠内无水时，换另一组土工布进行下一组试验.

选择透水性和过滤性能较好的短纤针刺非织造土工布，取其中5种规格，面密度μg分别是100,150,200,300,400 g/m2，每种规格分别设置4组层数n，分别为1层、2层、3层、4层，共20组试验.表1为试验组次表，表中t为土工布的单层厚度，O90为特征孔径，K为单层渗透系数.

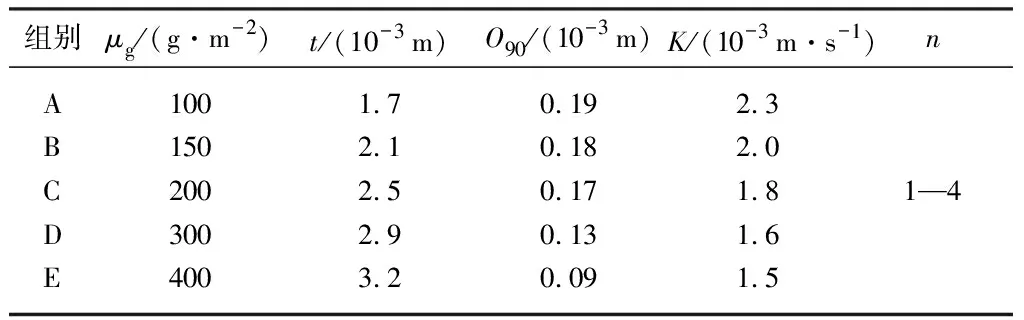
表1 试验组次表

2 汇流量计算公式

2.1 基础公式的选择

以土工布为反滤层的多孔管与以砂石料为反滤层的多孔管类似，都是汇集地表水，所以含有土工织物反滤层的多孔管汇流量计算表达式可在阿拉薇娜·努美诺夫完整式的基础上进行分析，

(1)

(2)

式中：Q为渗渠产水量，m3/s；L为渗渠长度，m；α为淤塞系数，一般不浑浊的河、湖水采用0.8，中等浑浊时采用0.6，浑浊时采用0.3，本试验水质比较清澈，采用0.9；H为多孔管顶部水头，m；h为多孔管内水位对多孔管出口所施水头，m，当多孔管内为大气压时,h=0；A为量纲为一的参数；D为多孔管直径，m；T为含水层厚度，m.

图2为cotx的计算值.

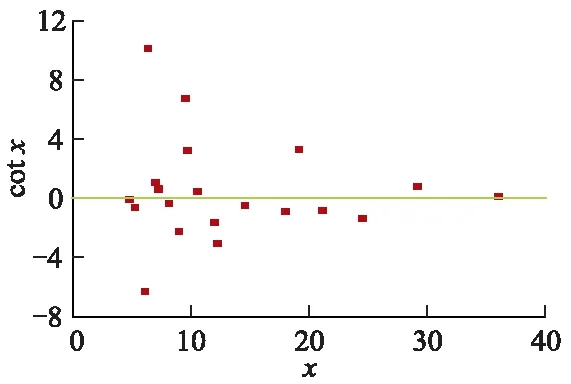
图2 cot x的计算值

对于含有土工织物反滤层的多孔管，管径D远大于含水层(土工织物)厚度T，则式(2)中D/T>>1，令x=(π/8)×(D/T)，由室内试验参数可知，cotx在一定的工况下存在着负值，如图2所示.根据对数函数的性质，当cotx为负值时，式(2)无意义.由此说明，式(2)对于量纲为一的参数A的计算不适用于含有土工织物反滤层的多孔管，因而需要通过理论分析和试验结果来总结出适用于有土工织物的多孔管汇流量的表达式.

2.2 量纲分析

含有土工布反滤层的多孔管汇流量的影响因素有：土工布的渗透系数K、土工布的层数n、压力水头H、多孔管汇流管长度L、特征孔径O90、淤塞系数α、流体密度ρ、运动黏滞系数υ、重力加速度g.由此，含有土工织物反滤层的多孔管的汇流量的一般表达式为

Q=f(K,t,n,L,O90,H,α,ρ,υ,g).

(3)

不考虑常量和次要因素可得：

Q=f(K,t,n,L,O90,H,α).

(4)

参考式(1)，并根据物理关系以及量纲和谐原理得

(5)

(6)

将f(β)视为一流量修正系数φ，则

Q=αφKLH.

(7)

下面将着重研究量纲为一的参数φ与土工布反滤层的特征系数β的关系.

2.3 计算公式拟合

结合具体试验数据进行拟合分析.在面密度μg为100,150,400 g/m2的短纤针刺非织造土工布，层数n=1，2，3，4，压力水头H=0.3 m和H=0.4 m的工况下，图3为流量修正系数φ与土工布反滤层的特征系数β的拟合关系，关系式为

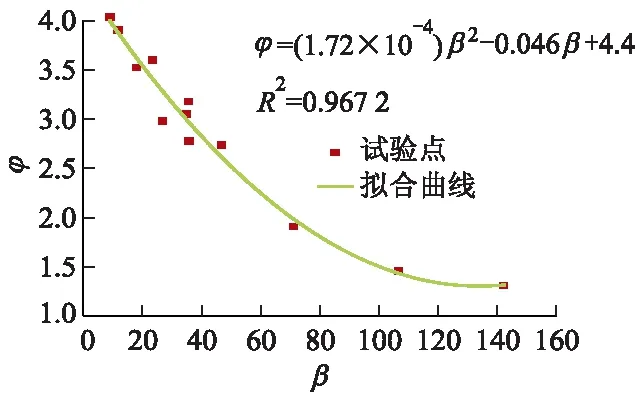
图3 流量修正系数φ与土工布反滤层的特征系数β关系图

φ=(1.72×10-4)β2-0.046β+4.4.

(8)

由此可得汇流量Q与土工织物反滤层特征系数β的关系表达式：

Q=[(1.72×10-4)β2-0.046β+4.4]αKLH,

(9)

即，

(10)

2.4 计算公式验证

为验证式(10)的可靠性与精确性，将试验数据实测值与计算值进行对比，鉴于没有这方面其他学者的试验资料，故无法用他人研究资料进行验证，所以笔者用面密度μg为200，300 g/m2的试验组进行对比.图4为室内试验实测出水量Qc与计算汇流量值Qe的对比图.从图中可以看出，数据点基本分布在1∶1线两侧，线性回归计算的修正后相关系数R2为0.923 4，证明室内试验汇流量实测值与式(10)的理论值高度相关，可以用于指导实际工程的设计计算.

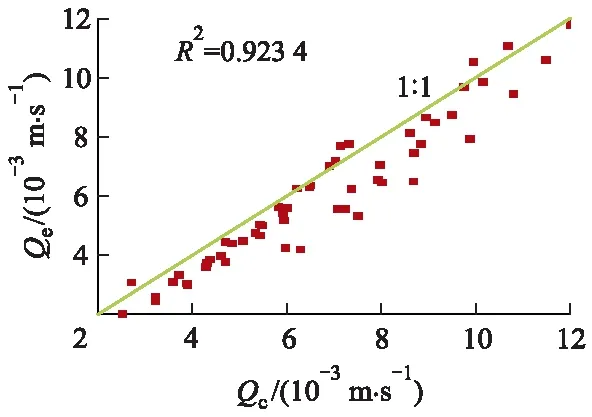
图4 实测汇流量与计算汇流量对比图

3 汇流量影响因素分析

3.1 土工织物层数对多孔管汇流量的影响

为了更好地反映土工织物的层数n与出水量Qc之间的关系.根据不同面密度组的试验结果进行分析，如图5所示.从图中可以发现，在其他条件不变的情况下，多孔管汇流量随着土工织物反滤层层数的增加而减小，且减小的幅度逐渐变缓.结合前文的理论分析，当其他参数一定时，土工织物反滤层特征系数β随着土工织物层数n的增加而增大，由式(9)可知，β增大时，φ减小，汇流量随之减小，与试验结果相符.

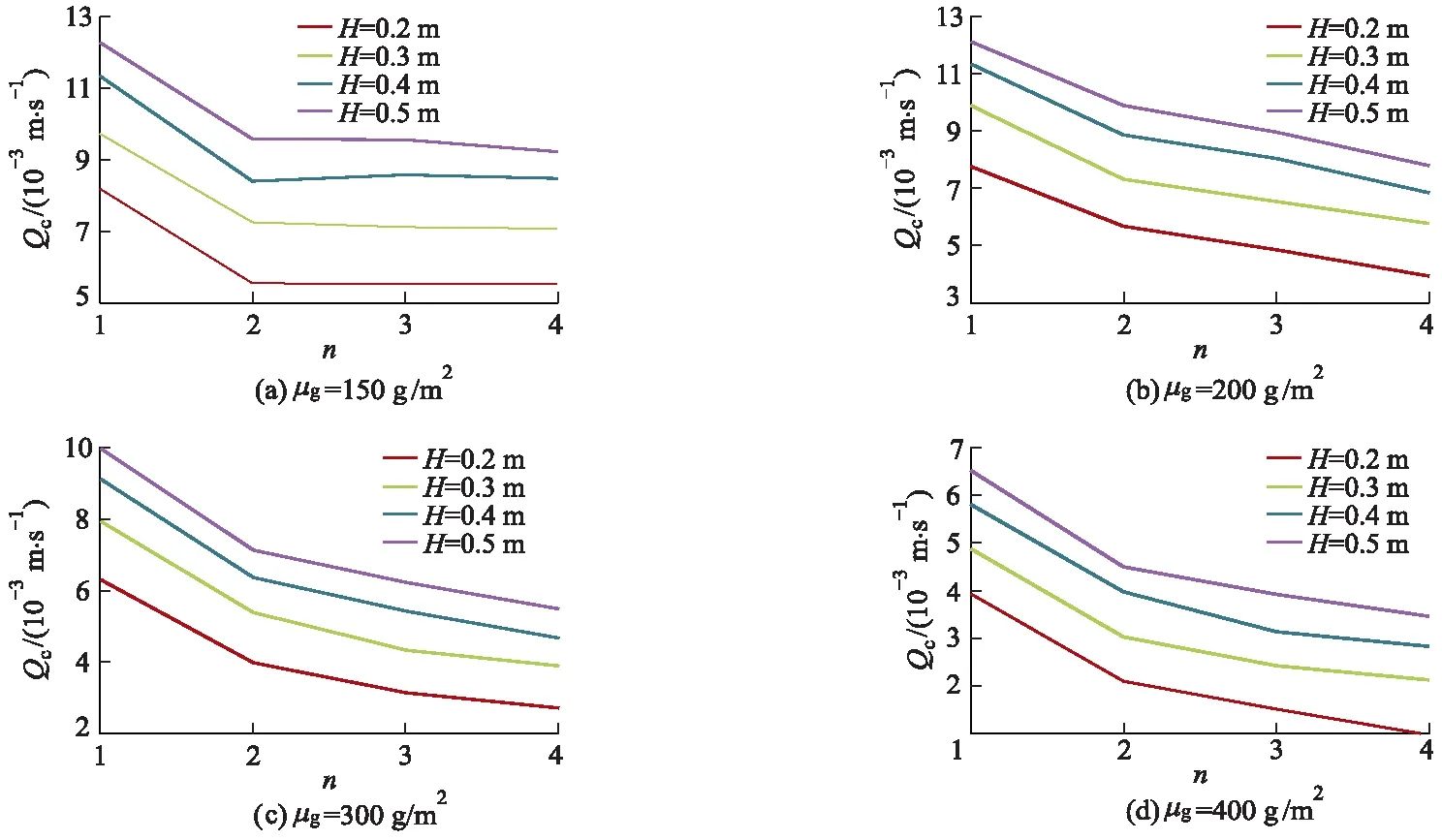
图5 不同层数土工织物下多孔管的出水量分布

产生上述现象的原因有2个：① 土工织物孔隙分布不均匀，当2层土工织物自由叠在一起时，2层土工织物接触面的孔隙不能完全匹配，即孔隙不能重合，所以当水流从上层土工织物流入下一层时，会受到阻力，造成一定水头损失，使水流流速变缓.除此之外部分流体沿层间间隙流动，渗径延长，水力损失增加，故2层土工织物时，多孔管的汇流量较单层土工织物时急剧减少.② 土工织物反滤层不同于砂石料反滤层，土工织物纤维在垂直水压力的作用下会被拉伸产生变形，随着拉伸应变的增加，滤层整体厚度减小，孔隙增大，导致孔隙率增大，渗透系数也随之增大.但随着土工织物层数的增加，反滤层整体的抗拉伸性能增强，滤层整体的拉伸应变减小，每层土工织物孔隙增大幅度减小，整体渗透系数逐渐变小，相应的汇流量也会减小.

3.2 土工织物面密度对多孔管汇流量的影响

图6为不同压力水头下，土工织物面密度μg对多孔管汇流量Qc的影响.从图中可以看出，随着面密度的增加，多孔管的汇流量随之增加.非织造土工织物是一种具有复杂微观结构的纤维材料，孔隙形状和尺寸的变化取决于层中纤维的空间分布、纤维缠绕程度、纤维形状和土工织物的制造过程，面密度增加，则单位面积的纤维将会增加，相应的特征孔隙O90将会变小，厚度t将会增加，进而导致渗透系数K减小.由理论分析可知，当特征孔隙O90变小、厚度t增加时，土工织物反滤层特征系数β会增大.根据式(9)可得，φ随β增大而减小.φ和渗透系数K减小，必然引起汇流量的减小，与实测结果相符.

图6 不同面密度土工织物下多孔管的出水量分布

4 结论与展望

1)经理论分析并结合试验数据拟合出汇流量与土工织物反滤层厚度、特征孔径之间的关系表达式，计算值与试验实测值相差较小，说明该表达式可用于指导实际工程的设计计算.

2)当其他参数一定时，含有土工织物反滤层的多孔管汇流量随着土工织物层数的增加而减小，且趋势越来越缓.当层数增加到一定数量，汇流量变化将趋于稳定.

3)当多孔管参数、压力水头以及土工织物层数一定时，多孔管汇流量随着面密度的增加而减小，即随着特征孔径的减小而减小.

4)本研究引入土工织物反滤层特征系数，由于该系数为纲量为一的参数，故所得的经验公式(10)在土工织物反滤层的一定参数内具有适用性，可为排水、集水实际工程中土工织物反滤层的设计提供理论支持，从而达到较好的技术经济效果，同时为具有土工织物反滤层的汇水管道的进一步推广应用提供帮助.