射流泵混合能力的FTLE评价方法

赵凯，程怀玉，龙新平，季斌，赖旭*

(1.水资源与水电工程科学国家重点实验室(武汉大学)，湖北 武汉 430072；2.水射流理论与新技术湖北省重点实验室，湖北 武汉 430072)

射流泵是一种利用湍射流的湍动扩散作用来传递能量和质量的特种流体机械与混合反应设备.射流泵内的混合通常是通过高速射流卷吸低速流体在射流边界层内由旋涡诱导产生的掺混，是一种强剪切条件下的流动混合，相比其他混合方式，其混合能更加充分.在实际工程生产领域射流泵式混合装置得到了广泛的应用[1].国内外专家学者对如何评价射流泵的混合程度进行了相关研究，比如毕荣山等[2]利用2股流体的浓度来评价流体混合程度；SUBRAMANIAN等[3]使用平均速度剖面来描述自由射流与受限射流的混合程度；KAMRAN等[4]取平均轴向速度的径向分布图来反映混合程度的变化；PERUMAL等[5]利用动量修正系数来反映截面上的混合程度.但是，这些成果的研究对象均局限于2种流体介质，当将其运用于射流泵混合研究时，仅仅能表征射流与被卷吸流2股流体之间的混合.由于射流泵作为一种混合设备时一般存在于循环运行的装置中，在循环过程中更多的是在对已初步混合的流体进行进一步的掺混，此时若仍仅考虑射流与被卷吸流2股宏观流体之间的混合，而不考虑流体内部质点之间的混合，则无法全面反映射流泵作为一种混合设备的性能.因此，提出一种研究对象为流体内部质点而不局限于射流与被卷吸流的混合评价指标，对于提高射流泵混合效率具有重要意义.

有限时间李雅普诺夫指数[6](FTLE)是由经典李雅普诺夫指数变形而来的一种向量场分析技术，表征的是一段时间内流体质点与其周围质点运动轨迹之间的平均分离程度[7].目前，已有大量学者将FTLE引入流体力学的研究中，比如雷鹏飞等[8]基于FTLE场的脊线所定义的LCS，提取了圆柱瞬时启动过程中流动分离和旋涡演化时的物质运输作用；SHADDEN等[9]通过FTLE脊线确定射流启动涡环的边界，并清晰地刻画了流体被卷吸到涡环的过程；LIN等[10]使用FTLE方法研究了可压缩涡环(CVRs)的形成过程.

以上研究表明FTLE在识别流体结构、分析流场特征方面具有独特的应用价值.而FTLE所具有的表征质点间平均分离程度的物理意义能很好地反映位于质点位置的混合能力，因此将其引入射流泵混合能力的评价具有天然优势.

为研究射流泵作为一种混合设备所具有的混合特性，文中对一典型射流泵开展混合能力的研究，旨在提出一种计算以及评价的方法，为具有相似物理性质的流体混合研究提供参考.

1 射流泵数值模拟

1.1 射流泵结构与性能参数

研究对象选用章君强[11]试验所用射流泵模型，其结构如图1所示.

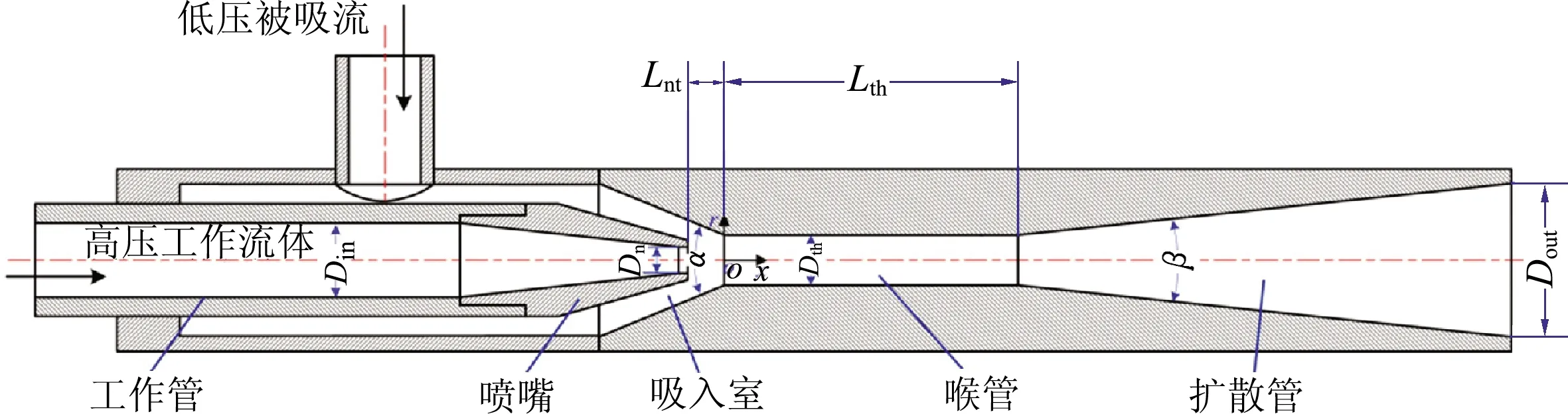
图1 射流泵结构简图

射流泵主要结构参数包括工作管直径Din、喷嘴出口直径Dn、喉管直径Dth、扩散管出口直径Dout、喉嘴距Lnt、喉管长度Lth、吸入室的收缩角α、扩散管的扩散角β.具体取值见表1.

表1 射流泵主要结构尺寸

在研究射流泵内部流动规律时，由于射流具有自模性，常使用量纲为一的性能参数计算射流泵基本性能，以获得更为普遍的规律，常用的量纲为一的性能参数包括流量比q、压力比h和效率η，各参数定义为

(1)

(2)

(3)

式中:Q为体积流量；P为流体总压；p为流体静压；ρ为流体密度；u为断面平均流速；z为高程；下标in，s，out分别表示射流泵的工作流体、被吸流体和混合流体.

1.2 控制方程与湍流模型

射流泵内部流动为湍流流动[12]，控制方程为连续性方程和Navier-Stokes方程，湍流模拟采用LES方法，其控制方程为

(4)

(5)

式中：ρ为流体密度，μ为流体的动力黏度.式(5)中最后一项τij为亚格子(subgrid-scale stress，SGS)应力项，文中采用WALE模型(Wall-Adapting Local Eddy-Viscosity Model)对SGS项进行求解.WALE模型由NICOUD等[13]提出，该模型能够返回正确的SGS黏度的壁面渐进特性，且能够较好地重现层流向湍流的转捩过程，目前已经被较多研究者用于数值模拟研究[14-15].

1.3 边界条件与计算设置

射流泵的工作流体和被吸流体入口都设置为速度入口，出口设置为压力出口，其余边界设置为无滑移壁面.其中计算域内的流体介质均设置为25 ℃水.文中计算工况数据均来自章君强的试验数据[11]，具体如表 2所示.

表2 计算工况

文中用SSTk-ω模型计算稳态初场，再使用LES计算非稳态流动.其中SGS模型选用WALE模型，WALE常数采用默认值0.5.用直接压力-速度耦合方法求解瞬态的LES控制方程，控制方程中的对流项用高阶格式求解，时间积分项用二阶后向欧拉算法来求解.时间步长取1.0×10-5s，计算收敛标准为10-5，内迭代次数为30.

1.4 计算域与网格划分

为确保管道内的流动发展稳定，消除进出口对喉管和吸入室等重要位置的数值模拟计算准确度的影响，将三通管道处流动简化成同轴受限轴对称流动，计算域如图2所示，工作流体管道、被吸流体管道以及出流管道均为管径的8倍.

图2 射流泵计算域

运用ICEM CFD软件，采用六面体单元的结构化网格对计算域模型进行网格划分.如图3所示，由于射流剪切层速度梯度较大，流动结构较为复杂，对吸入室与喉管部分区域的网格进行了加密处理.

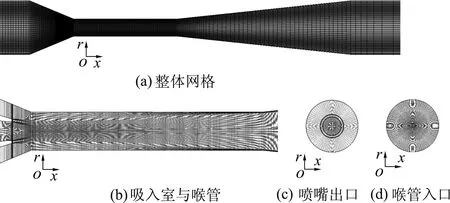
图3 射流泵网格

1.5 网格无关性分析

以数量分别为215万、460万和820万的3套网格，选取典型工况GK4进行了网格无关性分析.表3为压力比h和效率η的试验数据和计算结果，表中n为网格数，δh和δη分别为h和η的计算结果和试验结果的相对误差.3组网格的数值模拟结果都较为接近，均与试验值的误差不超过10%，分析造成该误差的原因在于仿真计算时将三通管道简化为轴对称流动，该简化造成了仿真条件比试验条件下的流动损失偏小，因此仿真的被吸管入口总压Ps偏小，从而压力比h偏大.

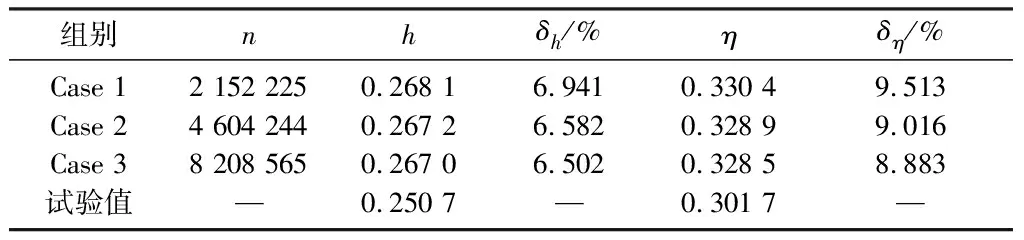
表3 网格无关性分析

2 FTLE计算原理与程序开发

2.1 FTLE定义与计算

对于某个时变流场，指定位置x，时刻t以及时间偏移量T，则其FTLE是一个标量值，代表该流场中在t时刻位于x处的相邻粒子，在经过时间T后的平均分离程度，计算式定义[16]为

(6)

式中：λ(Δ)为柯西-格林形变张量Δ的最大特征值，Δ为粒子流形空间梯度张量与其转置相乘得到的对称矩阵，计算式为

(7)

式中：FtT(x)为在时刻t位于x处的粒子，在流场中经过T后所在的位置，称为粒子流形.

湍流流场中FTLE的计算常使用有限空间差分法.该方法在数值模拟网格足够密集的情况下具有较高精度，其关键在于对式(7)中粒子流形的空间梯度张量进行离散.采用虚拟邻近节点的离散思想，使用虚拟邻近节点辅助计算梯度张量.具体如图 4所示，若需要计算位于节点(i,j,k)处的FTLE，首先在该节点沿x，y，z3个坐标轴方向上以指定差分距离取6个虚拟邻近节点，作为辅助计算节点.

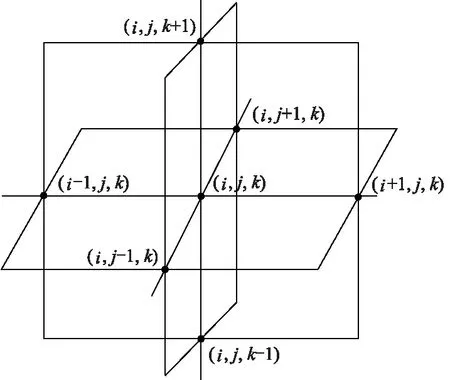
图4 虚拟邻近节点

然后对位于虚拟邻近节点上的粒子进行粒子追踪，求其时间偏移量T之后的空间位置，并代入粒子流形的空间梯度张量在三维空间离散后的计算式，即

(8)

(9)

(10)

(11)

式中：xi,j,k(t)，yi,j,k(t)，zi,j,k(t)为在t时刻位于编号为(i,j,k)的节点处的粒子的坐标分量；xi,j,k(t+T)，yi,j,k(t+T)，zi,j,k(t+T)为在t时刻位于三维空间中编号为(i,j,k)的节点处的粒子在流场中经过时间偏移量T后所在的位置的坐标分量.

2.2 粒子追踪计算

粒子追踪是FTLE求解的前提，也是影响计算速度的主要因素[16].对于流场中的粒子运动，其运动学方程的一般形式为

(12)

式中：x为粒子所在流场的空间位置；V为与时间相关的速度矢量场.

讨论数值解法时，采用求解初值问题的经典显式四阶龙格-库塔格式进行求解的差分格式为

(13)

由于数值模拟得到的是离散的速度矢量场，使用反距离加权插值法获取任意位置的粒子速度，其基本思想是距离越近，其属性越相似.插值公式为

(14)

式中：ui为网格节点上的速度矢量；di为网格节点到插值点的欧氏距离；ε为系数,一般取2.

2.3 FTLE计算程序

根据上述FTLE计算原理与粒子追踪算法，利用C++编程语言完成了FTLE计算程序的开发.计算程序分为预处理、粒子追踪以及FTLE求解3个模块.图5为程序运行的主要流程.

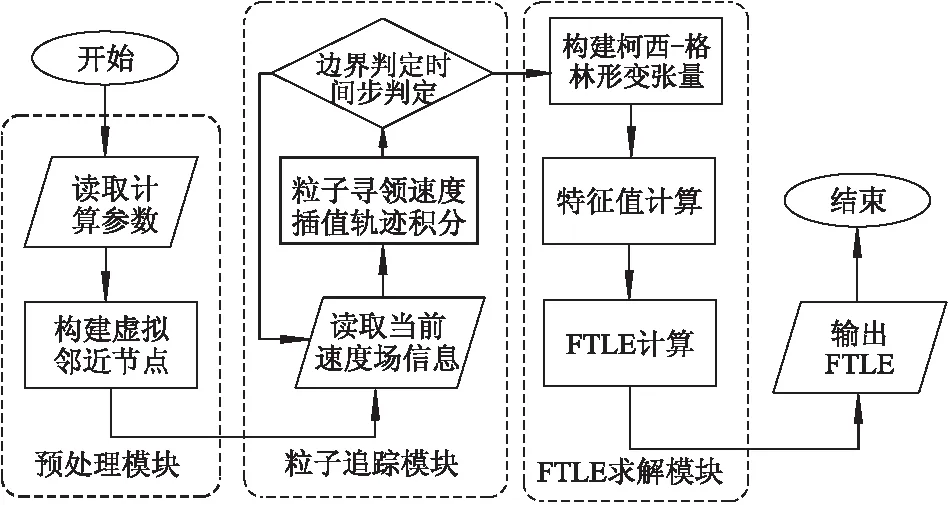
图5 程序流程图

3 射流泵混合能力评价

3.1 射流泵混合能力评价方法

由FTLE所反映的邻近粒子间平均分离程度的物理意义可知，每个取样点的FTLE计算结果能够代表该位置具有的混合能力，因此使用高分辨率的FTLE场可以直观地表达射流泵混合能力空间分布特征.为进一步探究不同流量比工况下的射流泵混合能力差异，将垂直于轴线截面的FTLE平均值作为射流泵在该位置的平均混合能力，并基于平均混合能力分析不同轴向位置的混合能力差异.

由于FTLE的计算结果为基于某一个时间段的速度矢量场进行的计算，计算结果为瞬时混合能力，因此需要考虑运行过程中的射流泵的混合能力随时间变化的情况.计算GK4工况下在如图6所示的典型截面1，2，3上基于不同时间段的FTLE，结果如图7所示.其中图7a为各典型截面上的FTLE场分布情况，虽然不同时刻的FTLE场存在细节上的差异，但总体形态特征相似，不影响基于FTLE场的定性研究.图7b为图7a对应的各截面上的平均混合能力am随时间T变化情况，可以发现截面平均混合能力也基本维持稳定.

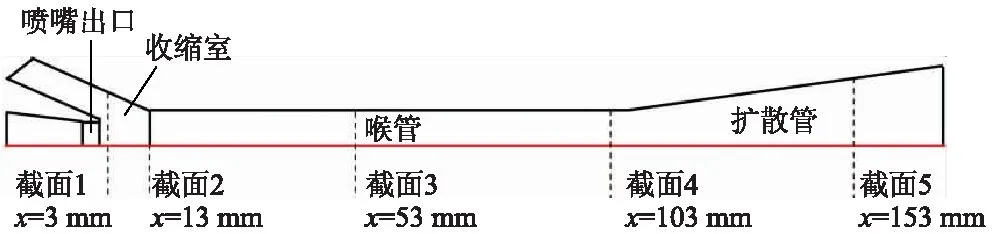
图6 典型截面位置

图7 基于不同时间段的FTLE计算结果

使用FTLE场描述混合能力空间分布特征，以及使用截面FTLE平均值代表不同轴向位置的平均混合能力时，其随时间产生的差异均可以忽略不计.因此，使用瞬态的FTLE计算结果对稳定运行的射流泵的混合能力进行评价.

3.2 射流泵混合能力空间分布特征

图8为GK4工况下轴线以及垂直轴线的各截面上的FTLE场.图9为平均混合能力am沿轴向距离x变化情况.在喷嘴出口位置截面(x=3 mm)上，强混合能力区域主要集中在射流与被卷吸流的剪切层，分布集中且面积较小，随着射流向下发展，混合能力较弱的被卷吸区域随收缩室的收缩而不断被缩小，同时射流剪切层的强混合能力区域不断扩散，此阶段平均混合能力沿轴向迅速增强，进入喉管后，强混合能力区域继续发展直至充满整个截面(x=28 mm)，此阶段平均混合能力增强速率逐渐放缓，并在强混合能力区域完全扩散时达到最大值.此后除了靠近内壁面区域维持较强的混合能力，其他区域的混合能力总体呈现不断衰减的趋势，平均混合能力沿轴向不断减小.

图8 各截面FTLE场

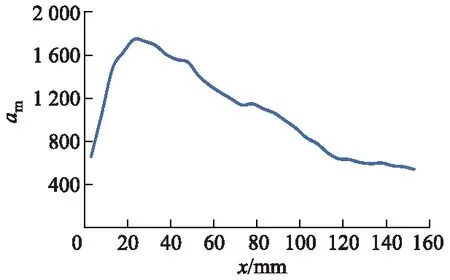
图9 平均混合能力沿轴向变化

根据射流泵混合能力空间分布特征可将流域内混合状态归纳为3类：剪切层处的高混合能力区域不断扩散的混合发展状态、高混合能力区域扩散至整个截面的混合完全发展状态、总体混合能力不断减弱的混合衰减状态.

3.3 流量比对射流泵混合能力的影响

图10为GK1—GK5工况沿轴线截面的FTLE场.在流量比q越小的工况，由剪切层发展的高混合能力区域能更好地保持形态，扩散趋势并不明显，处于混合发展状态的流域越长.随着流量比q增大，高混合能力区域扩散得越来越剧烈，导致处于混合发展状态的流域缩短，混合完全发展状态越来越靠近上游，在GK5(q=0.902)工况，射流几乎在刚进入喉管后就达到了混合完全发展状态.从整体上，虽然流量比的增大使得射流泵能迅速达到混合能力较强的混合完全发展状态，但此后的混合衰减过程也更为迅速，导致了整体处于较强混合能力的流域长度较短.

图10 GK1—GK5轴截面FTLE场

从GK1—GK5工况平均混合能力am随轴向距离x变化的情况进行定量分析也可以发现同样的规律.如图 11所示，虽然流量比增大可以加快平均混合能力的增强，但由于增长速度过快，并且在此后平均混合能力减小的速率也相对更快，因此能够维持具有高强度平均混合能力流域的长度很短；相反在小流量比情况下，虽然平均混合能力增长较慢，但这也导致了喉管内相当长的一段流域处于接近最高平均混合能力的状态，并且达到最高点后衰减的速率也相对较慢，进一步地延长了高混合能力流域的长度.

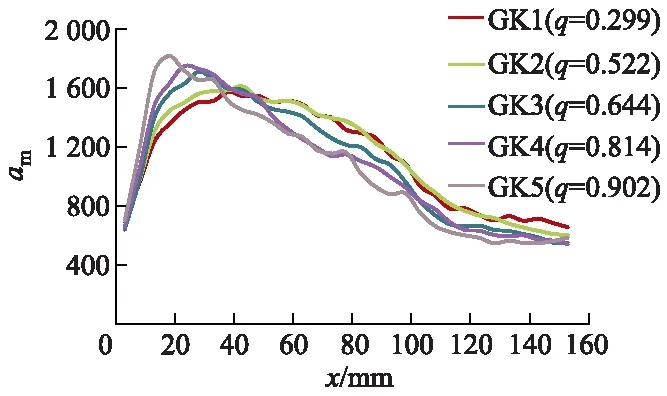
图11 GK1—GK5平均混合能力沿轴向变化

4 结 论

通过数值模拟得到射流泵内部流动的离散速度矢量场.提出了一种虚拟邻近节点FTLE求解方法，并使用C++完成了求解程序设计.基于该求解程序计算提供的FTLE场，提出了一种射流泵混合能力评价方法，使用此评价方法深入分析了一种典型射流泵的混合能力，得到了以下结论：

1)稳定运行状态下的射流泵的FTLE场的总体形态特征不受时间影响，各位置的平均混合能力随时间变化很小，可以利用瞬态的FTLE计算结果对稳定运行中的射流泵混合能力进行评价.

2)处于混合发展状态的流域内随着剪切层处的高混合能力区域不断扩散，平均混合能力逐渐增强；在混合完全发展状态时平均混合能力达到最强，在混合衰减状态，各处的混合能力总体衰减，平均混合能力不断减弱.

3)流量比从平均混合能力大小以及变化趋势2个方面来影响射流泵的混合.流量比越大，平均混合能力沿轴向增长越快，衰减越快，射流泵内持续高强度混合能力的流域长度越短.