基于离散型鲸鱼优化算法的AGV与机器集成调度方法
2022-06-23邹裕吉宋豫川王馨坤
邹裕吉,宋豫川,王 毅,王馨坤
(重庆大学 机械传动国家重点实验室,重庆 400044)
随着“中国制造2025”的提出,以及云计算、互联网和大数据等信息技术的发展,大规模定制化和多品种小批量的生产模式逐渐成为主流。在这种以个性化为主的生产模式下,产品种类繁多,工艺流程复杂,合理的车间调度方案对于提高生产效率至关重要。在传统的柔性作业车间调度问题研究中通常不考虑工件的转移时间,导致这种调度结果并不是理论最优调度结果,对于实际生产的指导存在不足。AGV(automated guided vehicles)是一种高柔性、高可靠性及高效率的先进物流装备,在数字化车间中负责实现工件的转移[1]。在这种情况下,机器的调度和AGV的调度会相互影响,所以AGV和机器集成调度问题越来越受关注。
土耳其学者Ulusoy等[2-4]于1993年首先将AGV和机器集成调度作为研究对象,在不考虑AGV路径冲突的前提下,应用遗传算法求解调度问题,并建立了标准算例库。Abdelmaguid等[5]在Ulusoy的基础上提出一种精英保留策略,研究了6种交叉操作和3种变异操作的最佳组合以及交叉和变异最优概率范围。Zheng等[6]针对该问题,建立了混合整数线性规划模型,以最大完工时间为优化目标,提出禁忌搜索算法结合12种邻域结构求解该模型。Deroussi等[7]提出一种混合粒子群遗传算法用以解决柔性制造系统中AGV和机器集成调度问题,包含了一种基于AGV的解决方案。刘二辉等[8]提出一种改进花授粉算法求解AGV和机器集成调度问题,并研究了AGV数量对调度结果的影响。
以上研究为了将问题简化,都聚焦于AGV和机器的调度,着力于解决AGV和机器的任务指派、任务执行时序问题,将AGV的行驶道路设定为单道单向,并且不考虑潜在的路径冲突。当AGV的行驶道路为单道双向时,系统的运行效率将会得到提高,但路径冲突也会随之增加。路径冲突如果不解决,就会出现AGV碰撞以及路径被死锁等问题,打乱调度计划甚至造成生产系统瘫痪。因此,在AGV和机器集成调度问题中,考虑AGV路径冲突具有重要的现实意义。Said-imehrabad等[9]建立了一个由车间调度和无冲突路径组成的数学模型,提出一种二阶段蚁群算法,首先解决AGV的分配问题,然后再解决AGV的路径冲突问题。Shi等[10]考虑AGV运行时间、停车和转弯的影响,提出一种两阶段调度策略,首先通过Dijkstra算法规划路径,然后考虑AGV之间的约束关系并通过遗传算法对结果进一步优化。Lyu等[11]提出一种改进遗传算法求解柔性作业车间AGV和机器的集成调度问题,通过Dijkstra算法为AGV规划无冲突的最短路径,并把AGV数量当做变量研究最大完工时间的变化,若在算法中采用主动解码,其结果将会更优。
AGV和机器集成调度问题已经被证明是NP难问题的叠加[7],这类问题的解空间庞大且复杂,精确算法难以在可接受的时间内求得最优解,启发式算法更适合求解此类问题。鲸鱼优化算法是Mirjalili等[12]于2016年模仿座头鲸独特捕食行为提出的仿生算法,和其他智能优化算法相比,具有结构简单、参数少、搜索能力强且易于实现等优点,在航路规划[13]、港口拖船调度[14]及选址问题[15]等离散优化问题中的应用越来越多。
综上所述,传统的作业车间调度研究不考虑工件转移时间,无法满足当前生产模式转变所带来的新需求。同时,目前对于AGV和机器集成调度问题的研究大多不考虑路径冲突,与实际生产情况不符,而考虑路径冲突的研究大多采用分阶段的策略进行求解,并非真正意义上的集成调度。鲸鱼优化算法作为一种启发式算法在离散优化领域取得了一定的成功,但在调度领域的应用不多。为了实现无冲突路径的AGV和机器集成调度,笔者首先以最大完工时间为优化目标,建立数学模型;然后,为了求解该模型,将鲸鱼优化算法应用在集成调度领域,对于鲸鱼优化算法存在的不足,提出针对性的改进方法,即基于时间窗和Dijkstra的离散型鲸鱼优化算法;鲸鱼优化算法作为算法迭代的整体框架,基于时间窗的Dijkstra算法用于算法解码过程中AGV的路径规划;最后,通过标准算例对比实验和柔性算例实验验证了所提算法的性能。
1 问题描述及数学模型
1.1 问题描述
假设有n个需要加工的工件,m台用于加工的机器,k台用于运输工件的AGV。每一个工件有ni道工序,每道工序至少可由一台机器加工,选择不同的机器加工时间一般不同。每台AGV可以在任意两台机器以及仓库之间运输工件,运输的路线一般是起点和终点之间可行的最短路径,运输时间取决于运输路线的长度以及路途中的冲突状况。AGV完成一个运输任务分为空载和负载两个阶段,空载阶段AGV需要从当前位置行驶到工件当前所在的位置;负载阶段AGV将工件从当前位置运输到加工机器所在位置。
已知条件有:AGV数量、各机器的位置、所有工序可选择进行加工的机器及对应的加工时间、任意两节点之间的距离(当不可通行时为无穷大)。要求在满足一定的约束条件的情况下达到优化目标的目的,具体可分为以下几个子问题:为每一道工序分配机器和AGV;为各机器安排加工任务序列和各加工任务开工时间;为各AGV安排运输任务序列和各运输任务开始时间。此外,为了简化问题,存在以下假设:
1)在开始时刻,所有AGV和工件都在仓库,AGV随机出发,有先后顺序。
2)每台AGV均可运输所有工件且一次只能运输一个工件。
3)AGV的行驶速度恒定不变。
4)每台加工机器的工件缓冲区无限大。
5)AGV完成运输任务后可以停靠在机床旁边,不需要返回仓库。
6)每台机器一次只能加工一个工件且一旦开始加工就不会中断。
7)加工准备时间以及装卸工件的时间算在加工时间中。
8)所有路段同一时刻只允许一台AGV通过,且任意路段可容纳AGV的车身,不存在AGV占用两个车道的情况。
9)同一个工件的工序有先后约束,不同工件之间的工序无约束。
10)不考虑AGV故障、电量等因素,也不考虑机器故障。
11)所有工件都增加一道虚拟工序,加工时间为0,加工机器的位置为仓库位置,便于处理将工件运送回仓库。
1.2 数学模型
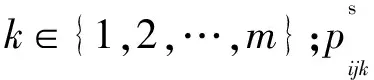
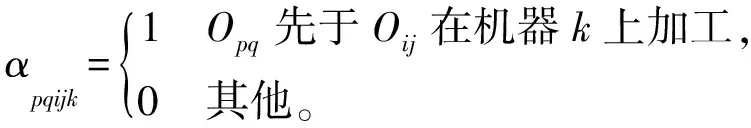

目标函数如下:
f=min(max(C1,…,Ci,…,Cn))。
(1)
约束条件如下:
1)任意工序都只能由一台机器完成加工。
(2)
2)任意一道工序最多只由一台AGV负责运输。
(3)
3)AGV空载出发时间不早于AGV上一次运输任务结束时间和工件开工时间。
(4)
(5)
4)AGV空载结束时间为空载出发时间与空载运行时间之和。
(6)
5)AGV负载出发时间不早于AGV空载结束时间和工件完工时间。
(7)
(8)
6)AGV负载结束时间为负载出发时间与负载运行时间之和。
(9)
7)某工序的开工时间不早于负载结束时间和机器前序工序的完工时间。
(10)
(11)
8)工序的完工时间为开工时间和加工时间之和。
(12)
9)工件的完工时间为AGV将其运送到仓库的时间。
(13)
10)某个路段有AGV进入之后,在该AGV驶出该路段之前,不允许其他AGV从该路段出口驶入。
(14)
11)同一时刻任意一个节点只能容下一台AGV。
(15)
2 算法描述
2.1 基本鲸鱼优化算法
鲸鱼优化算法是Mirjalili通过座头鲸独特的泡泡网狩猎方式抽象而来,种群中鲸鱼的最优位置就是算法所获得的最优解,迭代过程主要分为两个阶段:探索阶段和开发阶段,通过|A|和1的大小关系来区分[12]。

(16)

(17)
式中:r1是0到1之间的随机数;f为当前迭代次数;fmax为最大迭代次数。
当|A|≤1时,算法侧重于局部开发,鲸鱼个体向当前种群最优鲸鱼个体靠近,有收缩包围和螺旋更新两种靠近方式,为了实现这两种方式的同步,引入概率p去判断应该执行哪种更新方式。
(18)
D=|CXbest-Xt|,
(19)
C=2·r2。
(20)
式中:D为更新步长;b为控制螺旋线形状的常量系数;l为[0,1]范围服从均匀分布的随机数;r2为0到1之间的随机数。
当|A|>1时,算法侧重于进行全局搜索,鲸鱼个体向当前种群中一个随机选择的鲸鱼个体靠近。
Xt+1=Xrand(t)-A·D,
(21)
D=|C·Xrand-Xt|。
(22)
鲸鱼优化算法作为新型群智能优化算法,存在结构简单、参数少、搜索能力强且易于实现等优点,但也有群智能优化算法的通病,如收敛速度慢、容易陷入局部最优及收敛精度较低等。针对以上缺点,笔者结合车间调度问题的特点提出一种改进型鲸鱼优化算法。
2.2 离散化改造
为了更加清晰地描述问题,此处引入一个实例加以说明,各工件的信息如表1所示。
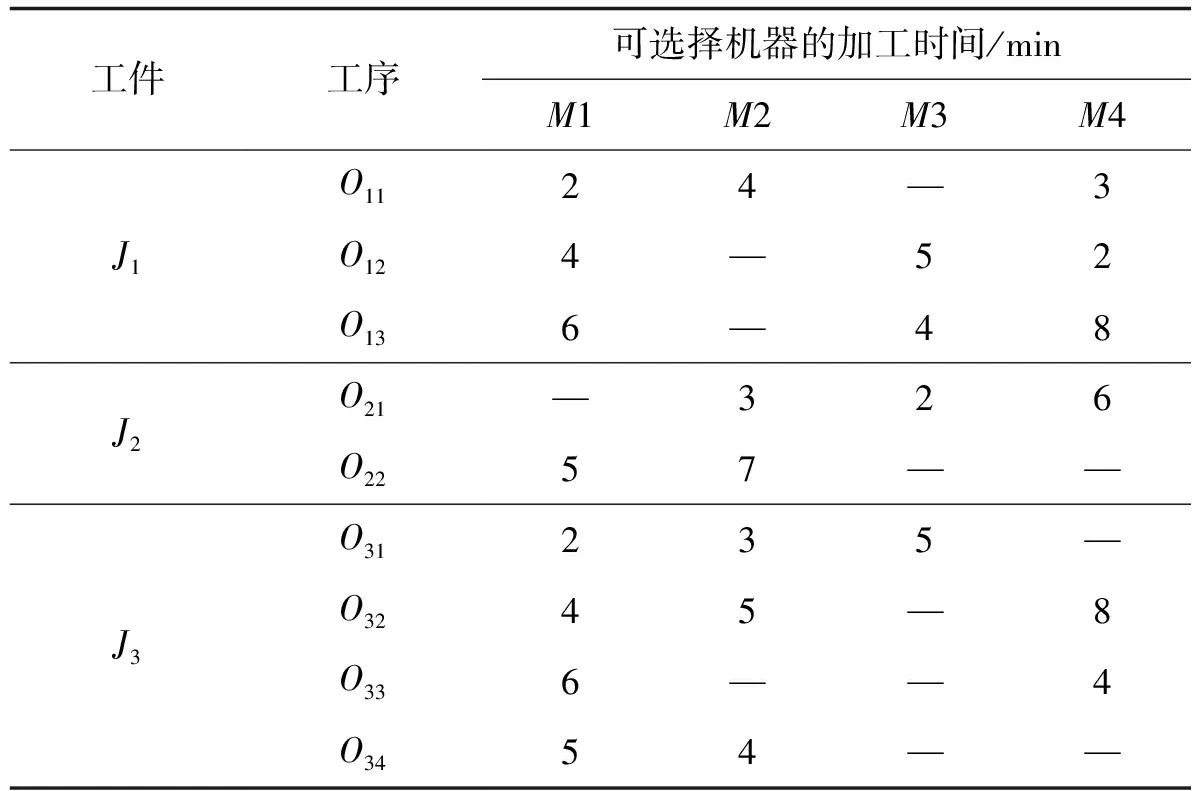
表1 加工信息
2.2.1 问题编码
作业车间机器和AGV共同调度问题中的调度子问题包含3个部分:工序排序、机器分配和AGV分配。笔者采用三段式编码,由3条基因串组成:第1条为基于工序的基因串,第2条为基于机器的基因串,第3条为基于AGV的基因串。基因串中每个位置值的取值范围为[-δ,δ]。由于引入了Levy步长更新鲸鱼个体,如果δ取得过小,更新后的个体工序序列基因值相对大小变化较大,导致个体被破坏;如果δ取得过大,则会导致Levy步长策略效果不明显,一般设为2~5之间的数。图1所示为一个合法的编码。
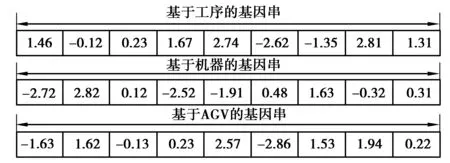
图1 个体连续编码示意图Fig. 1 Schematic diagram of individual continuous coding
2.2.2 编码转换
鲸鱼优化算法的解空间是连续空间,然而调度问题是离散组合优化问题。为了使得鲸鱼优化算法适用于调度问题,需要将连续的解空间映射到离散的解空间。由于工序排序、机器选择和AGV选择的约束不同,需要采取不同的转换机制。
采用LPV(largest position value)规则[16]对工序序列进行解空间的转换。具体的操作过程为,首先给所有基因从左至右安排一个从1开始的固定ID与之对应,然后将他们按从大到小的顺序排序,最后根据每个基因对应的ID得到一个新的基因串,按照每个工件的工序数转换为可以用以解码的序列,过程见图2。
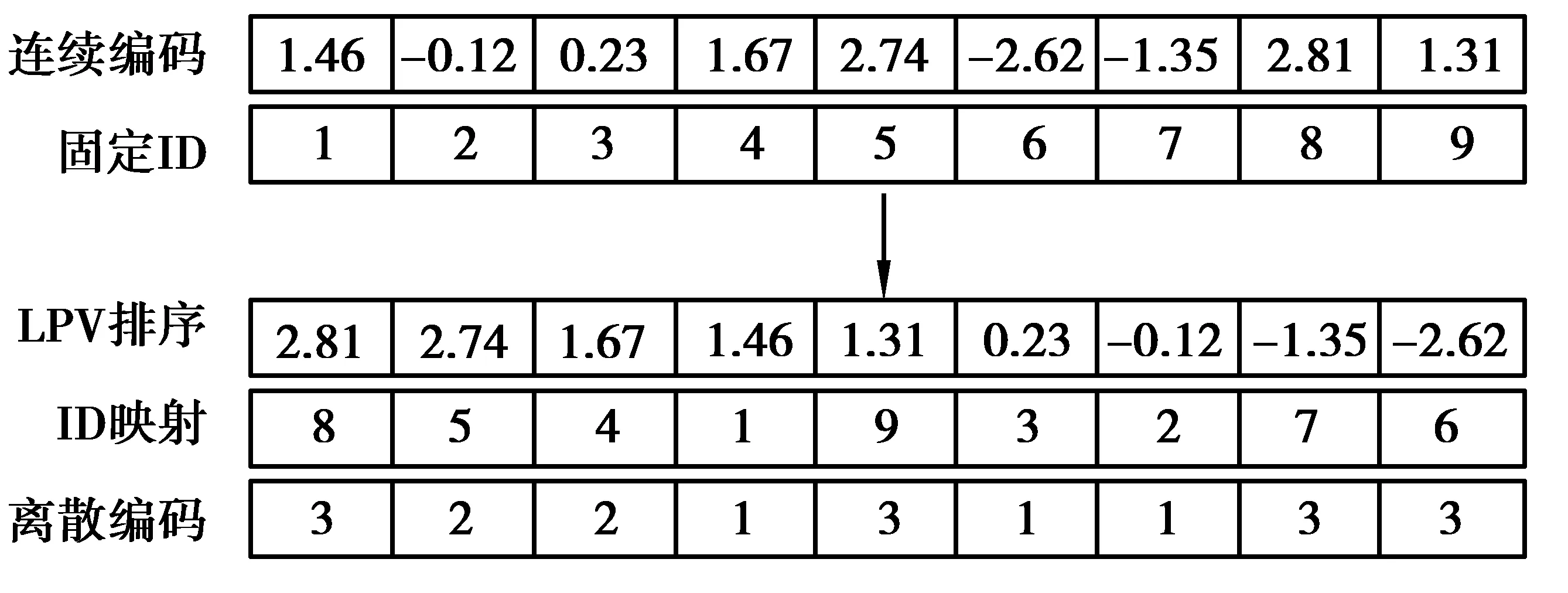
图2 LPV转换示意图Fig. 2 LPV conversion diagram
图2中,离散编码中的值表示的是工件号,从左至右出现的次数表示的是工序,第1个3表示的是工序O31,第2个3表示的是工序O32。
对于机器和AGV的解空间转换,采用文献[17]的方法。首先根据式(16)将连续的编码转换为离散编码,然后根据工序可选机器和AGV序列,转换为具体的机器和AGV编号。同时,通过逆运算实现从离散空间映射到连续空间,具体见式(23)。在AGV和机器基因串中,从左至右依次为从第一个工件到最后一个工件每一道工序对应的机器和AGV。具体见图3和图4。
(23)
式中:m(i)为连续编码的基因值;z(i)为该工序可选的加工机器数或者AGV数;u(i)为得到的离散基因值。
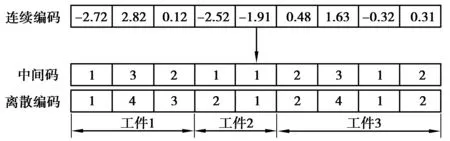
图3 机器编码转换示意图Fig. 3 Schematic diagram of machine coding conversion
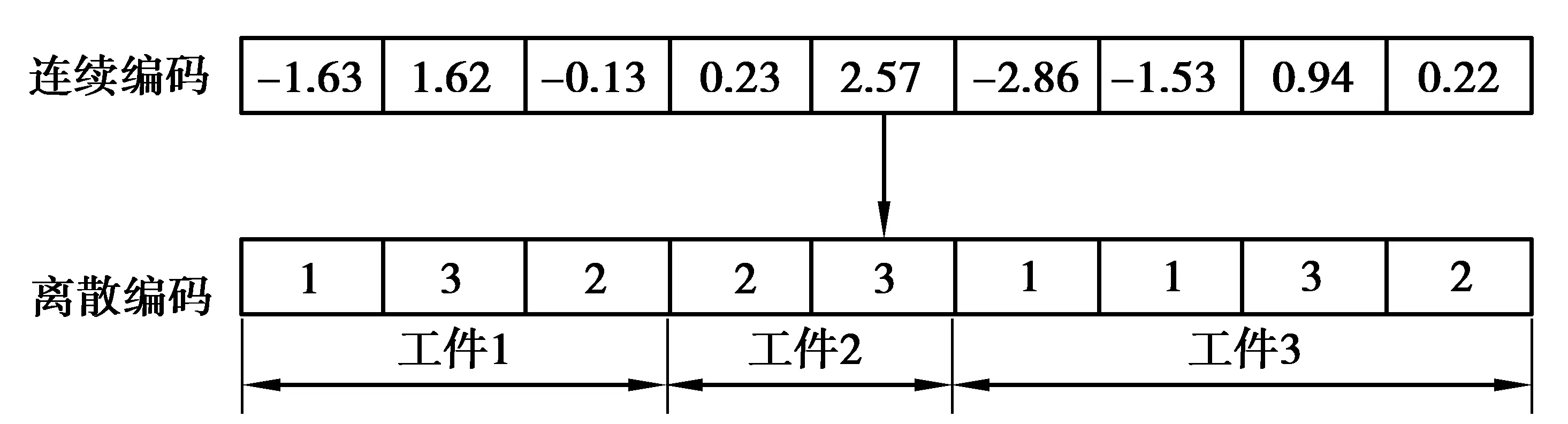
图4 AGV编码转换示意图Fig. 4 Schematic diagram of AGV encoding conversion
基于机器的基因串前3个基因值为工件1对应的3道工序对应的机器,图3和4表达的意思为:工件1的3道工序分别选择1,4,3号机器进行加工;基于AGV的基因串与基于机器的基因串类似。AGV的基因串前3个数字的意思为:工件1 3道工序分别选择1,3,2号AGV进行运输。针对机器和AGV共同调度问题,上述编码及其转换方式不会产生非法解。
2.2.3 规则调整
算法迭代过程中,可能会导致鲸鱼个体的某些维度越界。在原始鲸鱼优化算法中,每一轮迭代完成以后才会对越界个体进行调整。然而这种处理方式会导致一些问题,如在鲸鱼个体迭代过程中可能会选中越界的个体作为位置更新的基准,进而造成更多个体越界,不仅会增加算法的运行时间而且还会导致一些非越界个体被破坏。因此,选择在个体位置更新以后就进行个体越界的调整。原始鲸鱼优化算法中,将越界的维度设置为最大值或者最小值,当越界情况较多时,导致个体之间相似度越来越大。因此,可以将越界的维度设置为接近边界的一个值。具体调整规则见式(24)。
(24)
式中X(i)表示个体X的第i个维度。
2.3 种群初始化
初始化种群对于进化算法来说十分重要[18],初始解的质量和多样性对于算法的求解精度和收敛速度有非常大的影响。这里提出一种扩展GLR选择方法结合混沌映射和对立学习的种群初始化方法。
如果在生成初始解的时候,考虑各机器和AGV的工作时间与负载均衡可以大大提高种群的质量。在FJSP(flexible job-shop scheduling problem)问题上GLR(global, local, random)机器选择方法[19]被证明是一个比较有效的方法,该方法在随机生成50%个体的基础上,考虑工作时间与负载均衡,使用全局选择方法生成20%的个体。在该方法中,首先随机选择一道工序,将所有可加工机器已工作时间加上该工序的加工时间,然后选择目前加工时间最小的那个机器作为本道工序的加工机器并更新其加工时间。局部选择方法生成30%的个体,在该方法中,首先随机选择一个工件,为该工件的所有工序选择机器,按照全局选择的方法进行选择机器,不同的是,当一个工件所有工序都选择了对应的机器后,将所有的机器运行时间置零。该方法也应用在AGV的选择上,在AGV序列初始化时,为了减少计算量,在计算AGV的运行时间时不考虑冲突。
由于对于优化问题的全局最优解没有任何先验知识,初始种群应该尽可能地均匀分布在解空间中。所以增强初始种群的多样性以奠定算法全局搜索的基础一直是算法优化的一个方向。目前,大多数研究主要采用混沌映射策略和对立学习策略来增强智能优化算法初始种群的多样性。Ewees等[20]提出一种基于混沌映射的多元宇宙优化算法用以提高算法的全局搜索性能;Shen等[21]提出一种基于PSO和混沌映射的多种群优化算法;Alamri等[22]提出一种对立学习策略对鲸鱼优化算法进行改进。混沌映射和对立学习在改进算法上取得了许多成功,但是由于有很多混沌映射和对立学习方法可供选择,所以选择什么方法可以最大程度上提高算法性能是一个值得研究的问题;Elaziz等[23]使用基于差分进化算法的超启发式算法选择混沌映射方法和对立学习方法及其比例以得出最优组合,通过对35组标准函数的测试证明了其结论的可靠性。在经过GLR方法生成个体的基础上使用高斯映射和标准对立学习且比例为25%的策略生成初始化种群。高斯映射和标准对立学习表达式见式(25)(26)。
(25)
(26)
2.4 Levy飞行策略和阈值
Levy飞行是一种服从Levy分布的随机搜索路径,Levy分布是法国数学家Levy提出的一种概率分布。由于Levy分布是一种重尾分布,所以Levy飞行是一种短距离和偶尔长距离相间的搜索方式。随着Levy飞行在连续优化领域取得大量成功,近年来逐渐有学者将其应用到组合优化问题的研究中。王学武等[24]提出一种结合Levy飞行的粒子群算法以解决点焊机器人的路径优化问题;徐坤等[25]提出一种Levy飞行模式与蚁群算法的信息素更新方式相结合的算法用来解决TSP问题;Liu等[26]将levy飞行结合差分进化算法用来解决JSP问题。以上表明Levy策略在解决组合优化问题上也有较优异的表现。鲸鱼优化算法在迭代后期a逐渐减小,算法容易陷入局部最优。因此,将Levy飞行策略引入到算法迭代后期,增强其跳出局部最优的能力。同时,在算法的探索阶段引入Levy飞行策略可以增强算法的全局搜索能力。
X(t+1)=X(t+1)+[r-1/2]⊕L。
(27)
式中:X(t)表示的是经过鲸鱼优化算法迭代以后的个体;[r-1/2]有3种取值,r是服从范围在[0,1]的均匀分布函数,当r<1/2时,[r-1/2]取-1;当r=1/2时,[r-1/2]取0;当r>1/2时,[r-1/2]取1;⊕表示的是Levy飞行操作。所采用的工序编码转换方式,本质上取决于各个维度的相对值大小,所以对于工序向量要对每个维度单独进行Levy飞行操作。Levy飞行具体的数学表达式见式(28)~(31)。
L(s)~|s|-1-β,0<β≤2,
(28)
(29)
(30)
(31)
式中:Γ是标准伽马函数;β一般取1.5。
阈值操作也是防止算法陷入局部最优常见做法之一。具体的做法为:在算法开始时设置一个全局最优保持代数g并令其等于零,然后在算法迭代过程中记录当前最优值保持代数,当g达到设置的阈值l时,用随机生成的个体代替50%较劣个体。阈值的设置对算法有较大的影响,当阈值设置过小时,算法不易收敛且导致算法复杂度增加;当阈值设置过大时,会造成算法收敛速度变慢。一般设为最大迭代次数的10%~15%。
2.5 局部搜索
在开发阶段,种群个体以当前最优个体为基准来更新自己的位置,对较优个体进行局部搜索可以较大提升算法求解精度和收敛速度。由于AGV设备比较昂贵,在车间中AGV数量往往较少。对于机器和AGV共同调度的问题,经常出现工件等待AGV运输的现象,合理地分配AGV对于减小最大完工时间至关重要。提出的局部搜索分为两部分:基于工序和机器的变邻域搜索和基于约束AGV的邻域搜索,把最迟完成搬运任务的AGV定义为约束AGV。
1)邻域结构N1:在其工序的基因串中,随机选择两个位置,保证这两个位置必须对应不同工件的工序,互换它们的位置。
2)邻域结构N2:在其工序的基因串中,随机选择两个位置,将后一个基因插入到前一个基因的前一个位置。
3)邻域结构N3:在其机器的基因串中,随机选择一个位置,保证该位置对应工序的可加工机器不唯一,从该工序的可加工机器中随机选择一个替换该位置的机器。
在以上3种邻域结构的基础上,基于工序和机器的变邻域搜索算法步骤如下。
步骤1 设置初始参数,将要进行变邻域搜索的个体设为初始个体X;当前迭代次数n设为1,最大迭代次数nmax设为5,p设为1,pmax设为3。
步骤2 判断是否达到循环终止条件n≥nmax,如满足,输出当前个体X;否则,转步骤3。
步骤3 在个体X的基础上随机选择一个邻域结构,得到一个扰动个体。
步骤4 在扰动个体X′的基础上进行变邻域搜索,其具体步骤为:
1)判断是否达到终止条件p≥pmax,如满足,输出当前解X′。
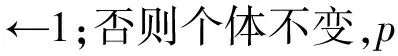
步骤5 令X←X′,n←n+1,转步骤2。
基于约束AGV的邻域搜索以基于工序和机器的变邻域搜索输出的个体为初始解,步骤如下。
步骤① 初始化参数,将初始个体设为X;当前操作的AGV任务编号n←1,nmax为总任务数。
步骤② 判断是否满足终止条件n≥nmax,如满足,输出个体X;否则,转步骤③。
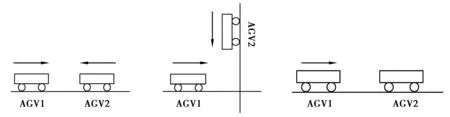
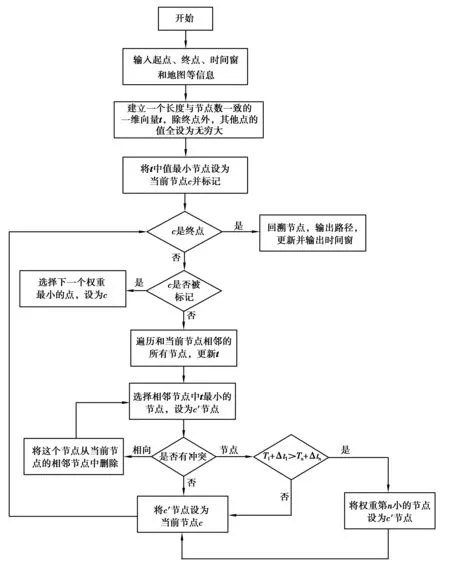
步骤③ 将当前任务分配给当前运行时间最小的AGV得到新个体X′;如果f(X′) 在算法对个体进行解码的过程中,工序确定加工机器以后,还需要根据工件的最早可开工时间以及机器的加工时间确定工序的实际开完工时间。在传统的车间调度方案中,工序的最早可开工时间为上道工序的完工时间,而AGV和机器集成调度问题要考虑工件的转移时间以及路途中可能遇到的路径冲突,因此要想确定工序的最早可开工时间,需要先给AGV规划无冲突路径,笔者采用一种基于时间窗的Dijkstra算法为AGV规划无冲突路径。 2.6.1 Dijkstra算法 在最短路径规划中Dijkstra算法能够从全局出发,具有较强的稳定性且算法简单[28]。Dijkstra算法要访问所有节点及其连通的节点,肯定可以求出最短路径,但是在节点和路段较多的地图中,求解时间会急剧增大。工厂环境中,AGV沿着固定的轨道行走,AGV也只需往返于各机器之间。因此,工厂环境下的地图节点和路段都比较少,Dijstra算法可以较好地发挥性能。另外,优化目标是最小化最大完工时间,AGV只有尽早完成任务工件才能尽早开工,基于贪心策略选择最短路径是全局最优解。因此,应用Dijkstra算法对AGV进行路径规划是一个较好的选择。 2.6.2 基于时间窗的Dijkstra算法 在多AGV参与的制造系统中,路径冲突是路径规划中常见的问题。只有解决了路径冲突才能实现真正意义上的集成调度。在工厂环境下的AGV冲突主要有:相向冲突、节点占用冲突和路口冲突。如图5所示。 图5 AGV冲突示意图Fig. 5 AGV conflict diagram AGV路径冲突本质上为AGV在时间或者空间上出现了重叠,时间窗方法是一种冲突预测方法,将地图以路段为单位记录锁定的时间。时间窗被证明是一个可以有效避免AGV冲突的方法。对于时间窗的表示方式为:[tin,tout,nin,nout],nin为进入该路段的节点,nout为离开该路段的节点,tin和tout分别为进入和离开的时间。这种表示方式可以包含两部分信息,节点的时间窗和路段的时间窗。由于AGV车身通过节点需要时间且要保持安全距离,因此会在一段时间内占用该节点。当两个节点时间窗有重叠时,说明这两个AGV有节点冲突。当两个路段时间窗有重叠并且两个AGV进入该路段的节点不同时,说明这两个AGV有相向冲突。 解决AGV冲突主要有两种方法:等待法和二次规划法。对于相向冲突,只有二次规划才能解决冲突。对于节点占用冲突和路口冲突,等待法肯定可以解决冲突,在时间窗上表现为将要等待的AGV的时间窗往后平移至没有重叠,二次规划也可以解决,但是可能会导致新的冲突甚至死锁。假设等待法多花费的时间为Δt,二次规划的行驶时间为T2。如果满足式(32),则采用二次规划法。 T1+Δt1>Tn+Δtn。 (32) 将时间窗嵌入到Dijkstra算法中,在对AGV进行路径规划的同时考虑避碰。为了减少计算量,对已经规划好路径的AGV不再更改路径。算法流程图图6。 图6 基于时间窗的Dijkstra算法流程图Fig. 6 Dijkstra algorithm flow chart based on time window 以最大完工时间最小为优化目标时,最优解必然在主动调度集中[29]。故采用主动解码,在不推迟已经被安排的工序开工时间的前提下,根据工件的最早可开工时间查找机器能够完成本道工序的空闲时间段进行插入式解码。传统的作业车间调度中,工件的最早可开工时间为前序工序的完工时间,而AGV和机器集成问题需要考虑工件的转移时间,所以工件的最早可开工时间为AGV负载结束时间。 T=2O(n)+O(N)+O(N·(n+f(n)))=O(N·(n+f(n)))。 (33) T=5O(N·n)+O(N)+O(N·(n+f(n)))+O(f(n))=O(N·(n+f(n)))。 (34) 综上所述,所提算法和原始鲸鱼优化算法的时间复杂度是一样的,在同样的运行环境下的运行时间在同一数量级。 算法流程见图7,具体流程如下。 步骤1 读入初始信息,包括工件的加工信息和工厂的地图信息。设置算法参数:种群规模NIND、最大迭代次数iitmax。 步骤2 根据种群规模和编码方式初始化种群。 步骤3 判断是否达到最大种群最大迭代次数,若达到,输出最优解;否则,计算所有个体最大完工时间并按照基于时间窗的Dijkstra算法进行路径规划,记录当前全局最优解,转步骤4。 步骤4 判断当前全局最优解保持代数是否达到阈值,如达到,转步骤5,否则转步骤6。 步骤5 随机生成种群规模50%的个体以替代种群中50%较劣的个体,转步骤6。 步骤6 更新鲸鱼种群。 步骤7 对当前种群较优个体进行局部搜索。 步骤8 保持种群规模,选择较优个体进入下一次迭代,转步骤3。 图7 算法流程图Fig. 7 Algorithm flowchart 为了确定和检验离散型鲸鱼优化算法在求解AGV和机器集成调度时的性能,笔者在MATLAB 2019a的编程环境,Inter(R) Core(TM) i5-8500 CPU,3.0 GHz主频,8.0 Gb内存的运行环境下开展以下实验: 1)标准算例对比实验。对Ulusoy提出的标准算例库进行实验,并与其他学者已有的研究成果进行对比。 2)柔性算例实验。对文献[11]提出的柔性作业车间AGV和机器集成调度算例进行实验。 表2中,LB by Ulusoy是由Ulusoy等[2]提出的下限法得到的理论最优值;LB by Zheng是由Zheng等[6]提出的改进下限估算法得到的理论最优值;STW是Bilge等[4]提出的滑动时间窗算法;AGA是Abdelmaguid等[5]提出的混合启发式遗传算法;MTS是Montane等[30]提出的禁忌搜索算法;PGA是Lyu等[11]提出的改进遗传算法;WOA为原始鲸鱼优化算法;IWOA是笔者提出的离散型鲸鱼优化算法。其中STW,AGA,MTS,RGA以及PGA均来自于文献中的原始数据。WOA和IWOA部分公共参数设置如下:种群规模80,最大迭代次数100。WOA的个体边界设为1,IWOA的个体边界设为3,最优个体保持代数阈值设为20。WOA和IWOA对每一个算例独立运行5次取最优解,和其他文献结果对比如表2和表3所示。 表2 t/p>0.25的算法结果比较 续表2 表3 t/p<0.25的算法结果比较 续表3 表2和表3中加粗的数据为各算法中最优结果。从表2和表3中的82个标准算例的对比中可以发现原始鲸鱼优化算法在这种解空间较大的情形下,算法很难收敛到全局最优解,性能表现较差。对其进行改进后,所有算例结果均不劣于原始鲸鱼优化算法,并有41个算例结果更优;相较于原始鲸鱼优化算法的结果,IWOA有19个算例结果提升了5%以上,其中有7个算例结果提升了10%以上。在表2的40个标准算例中,IWOA所有算例结果均不劣于其他学者采用的方法;其中算例EX101、EX103、EX44、EX94、EX104结果优于其他算法结果;特别的,算例EX22达到了理论最优解。在表3中的42个标准算例中,IWOA有15个算例达到了理论最优值;除算例EX840外,IWOA剩下所有算例的结果均不劣于其他学者提出的方法,其中算例EX441的结果优于其他算法结果。由此可以看出,在解决AGV和机器集成调度的问题时,IWOA和其他算法相比具有一定的优越性。 为了验证IWOA在柔性生产系统中的性能,对文献[11]中的算例进行实验,该算例中包含4个工件、6台机器,AGV数量从1增加到6。文献[11]中PGA运行参数为:种群规模设为80,最大迭代次数设为80,交叉率设为0.9,变异率设为0.1,算法独立运行10次取最好结果。为了更好地对比,IWOA和WOA的种群规模、最大迭代次数、独立运行次数和文献[11]设为相同的值。WOA的个体边界设为1,IWOA的个体边界设为3,最优个体保持代数阈值设为10。表4中v表示AGV数量,Cmax表示最大完工时间,单位为min,tcpu表示运行时间,单位为s,MT为平均最大完工时间,单位为min。 表4 柔性算例结果 从表4中可以看出,除了算例1中AGV数量为1时,IWOA的最大完工时间大于PGA,在其他算例中,IWOA的最大完工时间均不劣于其他两种算法;并且在各算例中可以看出,最大完工时间随着AGV数量的增加而减少,但增加到一定数量后不再变化,这是由于在AGV数量较少时,AGV数量为制约最大完工时间的主要因素,较多工件加工完成后需要等待AGV的运输,当AGV增加到一定数量后,加工设备成为主要制约因素,较多工件运输完成后需要等待加工机器。从表4中看出在加工机器数量相同的情况下,在算例1和算例2中,随着AGV数量的增加,IWOA的最大完工时间小于PGA,这是由于IWOA使用了贪婪解码,可以在较大程度上利用加工机器的空闲时间。在运行时间方面,WOA机制简单,运行时间最短,IWOA的运行时间最长。从最大完工时间可以看出,在IWOA中平均值和最小值相差较大,这是因为IWOA中加入了Levy飞行的策略,可能导致出现一些较差解,但同时也可以使算法拥有跳出局部最优的能力。 图8为算例1中AGV数量为3时的甘特图,ET表示AGV的空载行程。可以看出,所有工序开工时间在AGV负载结束时间、工件前序工序完工时间及机器前序工序完工时间之后,满足约束条件。 图8 最优调度结果甘特图Fig. 8 Optimal scheduling result Gantt chart 图9为算例1中AGV数量为3时各路段的时间窗图,用不同颜色区分AGV,可以看出,在任意时刻的纵坐标上不会出现同一辆AGV,说明AGV分配方案是可行的;在任意路段,不会出现不同AGV时间窗的重叠,说明AGV之间不会发生碰撞,IWOA可以为AGV规划无冲突的路径。 图9 各路段时间窗Fig. 9 Time window of each road section 图10是算例1中WOA和IWOA在AGV数量为3时的收敛曲线。WOA在迭代中后期目标值出现最大完工时间较大幅度减少,体现了WOA在后期具有较强局部开发能力的特点;但在这之后,最大完工时间不再改变,说明WOA陷入了局部最优。相对WOA来说,IWOA的初始种群的质量较高,验证了IWOA的种群初始化方法的有效性;IWOA在第25代就开始收敛到了89 min,说明算法有较好的收敛速度和收敛精度。 图10 算法收敛曲线Fig. 10 Algorithm convergence curve 针对柔性作业车间AGV和机器集成调度的问题,以最小化最大完工时间为优化目标建立了相应的数学模型,并提出一种离散型鲸鱼优化算法进行求解。在离散型鲸鱼优化算法中,提出一种结合GLR选择方法和混沌映射及对立学习的初始化策略,可以提高初始种群的多样性;对原始鲸鱼优化算法中的调整规则进行了改进,节省算法运行时间的同时不仅可以避免个体被破坏,还可以在出现较多越界情况时防止个体相似度增大;引入levy飞行策略和阈值重启操作,增强算法的全局搜索能力的同时增强算法跳出局部最优的能力;设计了一种局部搜索策略,增强算法的收敛精度。通过和82个标准算例以及柔性算法的仿真对比实验,证明了所提出算法的可行性和优越性。下一步将研究考虑完工时间、AGV行驶时间、AGV等待时间等AGV和机器集成调度多目标优化问题。2.6 多AGV路径规划
2.7 解 码
2.8 时间复杂度分析


2.9 算法流程

3 实验分析
3.1 标准算例实验
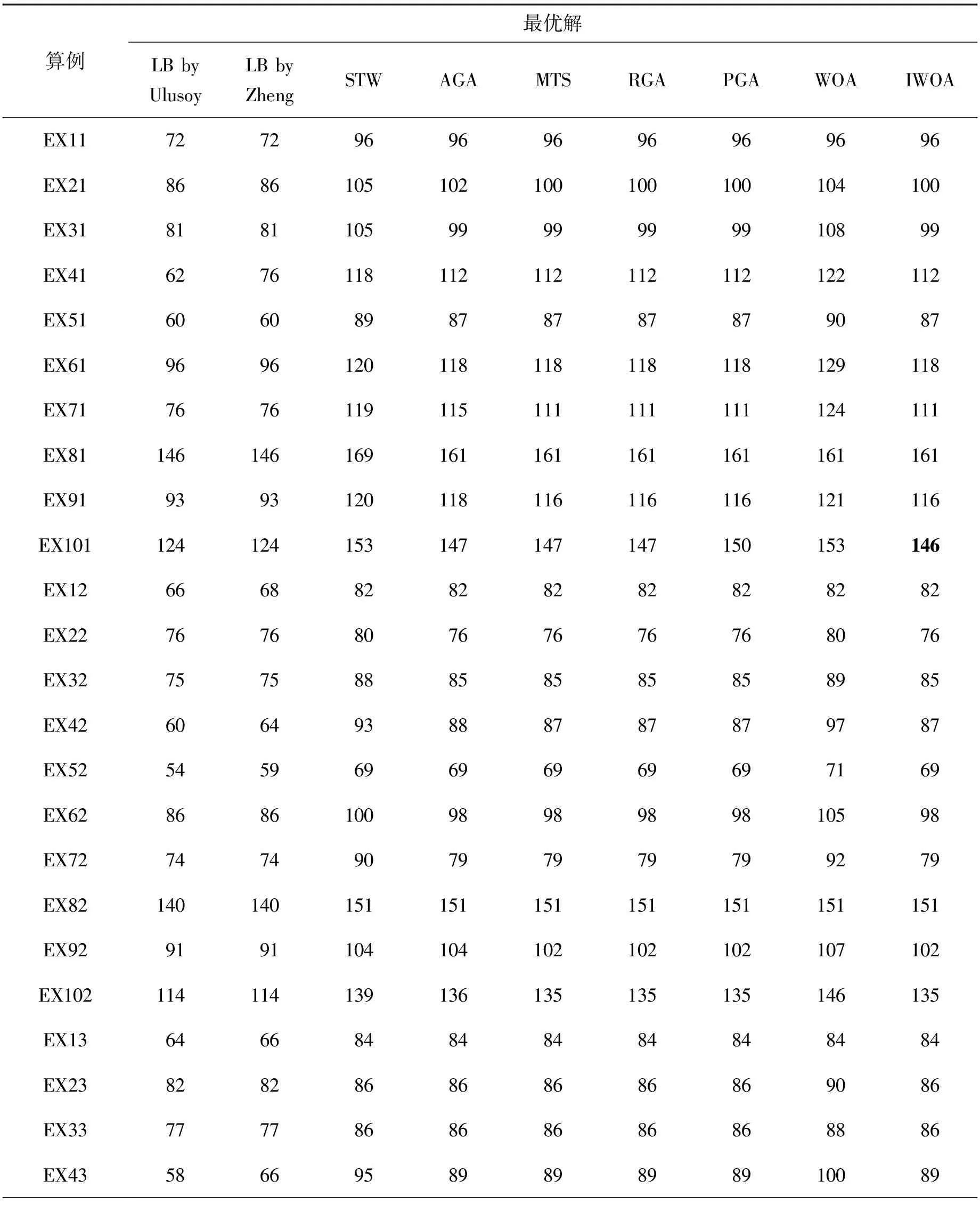

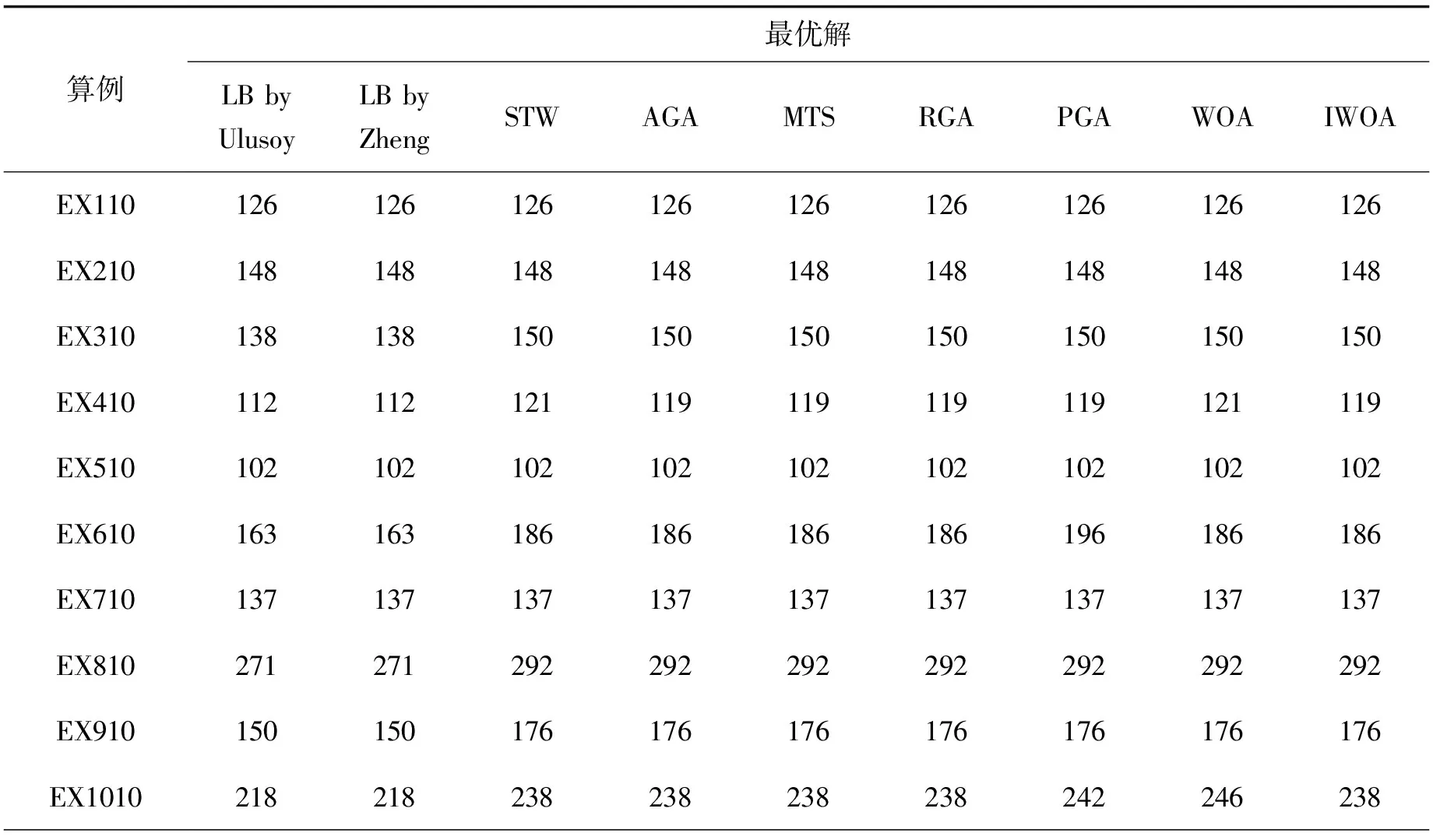

3.2 柔性算例实验

4 结 论
