基于深度学习的特征重要性因子分解机研究

廖 永,邹明峻,胡锐光

(广东工业大学 自动化学院,广东 广州 510006)

0 引言

目前广告点击率预测主要有传统模型和基于深度学习的模型。传统的模型一般以因子分解机(Factorization Machine,FM)为主[1],该方法利用矩阵分解的思想将交互矩阵分解为两个隐向量内积,使得在高维稀疏的特征下权重参数仍然能够被估计,并能够泛化到未被观察的特征。但由于在同一特征向量在不同的特征组合情况下所表示的意义应该有所不同。因此,域因子分解机(Field Factorization Machine,FFM)在FM 的基础上提出了“域”的概念来细化不同域下同一特征的隐向量表示[2]。随着注意力机制在图像和自然语言处理领域取得的重大成功,Xiao J 等[3]将注意力机制引入到FM 中,提出了注意力因子分解机(Attention Factorization Machine,AFM),加入注意力网络计算二阶特征组合的注意力权重,以区分不同特征组合的重要性。

随着计算资源和深度学习的发展,研究者们提出了很多基于深度学习的模型。ONN,PNN,NFM 等模型采用的传统模型和深度神经网络(Deep Neural Networks,DNN)前后相接的方式[4-6],先用传统模型训练得到低阶组合特征,然后将组合特征输入到DNN 得到高阶组合特征进行预测.Wide&Deep,DeepFM,DCN等模型采用双路的方式进行预测[7-9],通过传统模型得到低阶特征,增强模型的“记忆能力”。通过DNN 模型得到高阶特征,提高模型的泛化能力。

以往的FM 及其变形模型并没有考虑到对于不同的预测目标来说特征有强弱之分,也就是特征的重要性。针对FM 模型二阶组合特征的重要性问题,本文提出了一种特征重要性因子分解机FIFM 的广告点击率预估模型。从特征的重要性,即对预测目标来说特征有强弱之分的角度,使用挤压提取网络(Squeeze-and-Excitation Networks,SENET)的挤压提取模块和多头注意力模块动态地提取输入特征向量的重要性[10],从而区别有效的特征组合,增强因子分解机的学习能力。此外,结合DNN 和FIFM 分别获得高阶特征和低阶特征,进一步提高点击通过率(Click-Through-Rate,CTR)预测的准确率。

1 特征重要性因子分解机

通过目前对比前沿的广告点击率预测模型,可以发现已有的算法大多数是将经过Embedding 后的向量输入到因子分解机中以内积或哈达玛积的形式进行特征组合,但这种方法并没有关注到特征的重要性,将所有特征都视为同等重要。但对于每一个不同的预测目标而言,特征的重要程度都是不一样的。因此本文从特征重要性的角度对因子分解机模型进行改进。

FIFM 的核心思想在于通过压缩提取模块和多头注意力模块从不同的特征粒度计算输入特征向量的权重,并与输入向量结合重新表示成带权重的特征向量,从而在因子分解机中进行特征组合时得到有效的组合特征。通过对输入特征进行加权预处理,在因子分解机中进行组合时,组合特征会变得“强者更强,弱者更弱”,减少无关特征对预测目标的干扰,提高模型的预测准确率。

1.1 输入层和嵌入层

模型结构图如图1 所示,为了清楚起见,省略了LR部分。FIFM 主要包括以下部分:输出层(Input Layer)、嵌入层(Embedding Layer)、双通道权重计算层(Dual channel weight calculation Layer)、权 重 结 合 层(Combination Layer)、加权层(Reweighting Layer)、预测层(FM Layer)、输出层(Output Layer)。其中嵌入层是对稀疏的输入数据通过嵌入矩阵映射成稠密向量表示。

嵌入层的输入为原始特征的独热编码表示δ=[δ1,δ2,…,δf],输出是稠密的嵌入向量V=[v1,v2,…,vf],其中f 表示特征域的个数。独热编码和嵌入映射的数学表示如公式(1)和(2)所示。

1.2 双通道权重计算层

1.2.1 bit-wise 权重

不同的特征对预测目标的重要程度是有所区别的,如预测一条游戏广告是否会被用户点击时,通常爱好特征比性别特征具有更高的重要性。因此,本文利用SENET 的挤压提取模块,计算Embedding 向量的特征重要性,得到bit-wise 权重。如图2 所示,图中步骤①和②分别表示特征压缩,计算特征重要性下面是这两个的详细过程描述:

图2 挤压提取模块

(1) 特征挤压:通过对嵌入向量进行池化操作,得到嵌入向量的全局分布和统计信息,通常采用最大池化或者平均池化。将嵌入向量E=[e1,e2,…,ef]转化为向量U=[u1,u2,…,uf],ui表示第i 个特征向量的全局信息数值,也就是特征向量的重要信息。在这里采用效果较好的平均池化操作,其计算方式如公式(3)所示:

(2) 计算特征重要性:这一步的目的是利用统计信息向量U=[u1,u2,…,uf]计算出嵌入向量E=[e1,e2,…,ef]的特征重要性权重Obit=[o1,o2,…,of]。计算方法如图3 所示,将向量U 输入到两个全连接层得到权重向量Obit。其中,第一个全连接层的作用是对统计信息进行特征交叉的降维层,第二个全连接层的作用是将权重向量大小映射成f 的升维层。数学表示如公式(4)所示。

图3 特征重要性计算原理

其中,W1∈Rf×(f/r) 表示第一个隐藏层的权重参数,表示第一个隐藏层的权重参数,σ1,σ2分别代表第一层,第二层的激活函数,r 是全连接层的维度减少率。

1.2.2 vector 权重

为了计算vector-wise 的特征权重,需要把k×f 维的嵌入矩阵E 变换为f×k 维的矩阵Evec,如公式(5)所示。然后再将矩阵输入到多头注意力层计算特征的注意力权重。

多头注意力层包括注意力空间映射,自注意力计算,多头注意力及残差网络融合,权重计算四个部分。下面将详细介绍这四个部分内容。

(1)多头注意力空间映射。如公式(6)～(8)所示,这个步骤是将矩阵Evec通过矩阵WQi,WKi,WVi分别映射Q(Query),K(Key),V(value)空间得到新的矩阵表示Qi,Ki,Vi,i 表示第i 个注意力空间。

(2)自注意力计算。通过内积计算矩阵Qi,Ki的相关性并进行归一化计算,得到注意力分数,然后对矩阵Vi进行加权,得到矩阵Evec在单个注意力空间下的表示Headi,dk表示注意力因子的大小。其计算过程如公式(9)所示。值得注意的是,归一化操作也是一种捕获全局信息的方法,能够得到某一特征占所有特征的重要性权重。

(3)多头注意力及残差网络融合。如公式(10)～(11)所示,通过拼接n 个head,得到矩阵Evec在多头注意力加权下的表示。为了保留原始输入的信息,将向量U 经过残差矩阵WRi得到矩阵Ri。类似地,得到多头注意力下的原始信息如公式(12)所示。

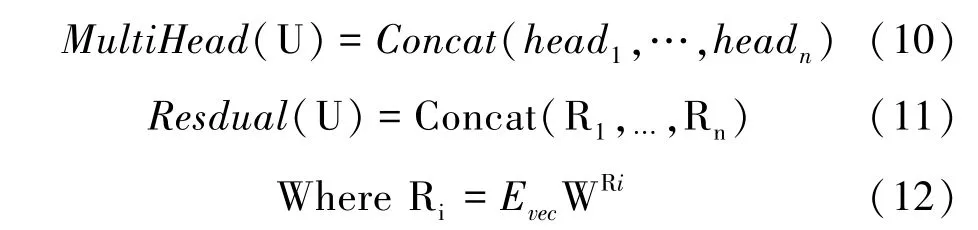
(4)权重计算。将MultiHead(U)和Resdual(U)输入到激活函数Relu 得到vector-wise 权重。计算方法如公式(13)所示。

1.3 结合层

在bit-wise 和vector-wise 权重结合之前,需要把通过转换矩阵Svec和Sbit进行降维操作,转化为权重向量,然后进行加和得到最终的权重向量wx。计算过程如公式(14)～(16)所示。

其中,wvec∈ℝD1,wbit∈ℝD2,D1=f×dv×n,D2=dv。Svec∈ℝD1×h,Sbit∈ℝD2×h,f 是特征域的个数,dv是嵌入向量的长度,n 是注意力的头数。

1.4 加权层

将结合层得到的权重对原始嵌入向量E=[e1,e2,…,ef]进行加权,得到新的嵌入向量表示VX=[vx1,vx2,…,vxf],如公式(17)所示。其中,mx,i表示权重向量mx中的第i 个标量。

1.5 因子分解机层

在因子分解机层,将新的Embedding 向量表示作为输入在这层中进行二阶特征组合,使得特征组合更合理,即得到与预测目标相关性更大的组合特征。其计算过程如公式(18)所示。

1.6 输出层

FIFM 的输出层将LR 部分和FM 部分求和用于最终预测。此处LR 部分使用的是经过重要性加权的嵌入向量VX=[vx1,vx2,…,vxf]。结合公式(18),得到FIFM 模型输出的整体公式如公式(19)所示。其中,w0是全局偏置。

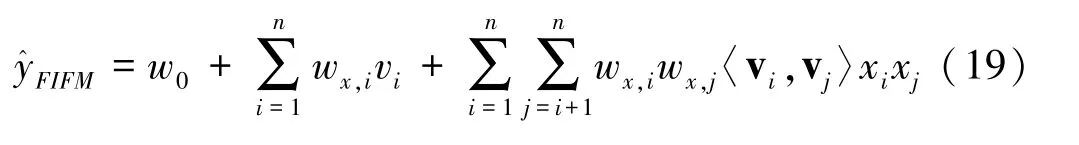
2 实验及性能评价

本节介绍实验的相关细节,通过在两个广告数据集Criteo 和 Avazu 上对进行实验,对FIFM 模型进行评价。实验内容包括:

(1)DIFM 与基线模型对比;

(2)Deep DIFM 与具有DNN 模块的基线模型对比;

(3)超参数设置对模型性能的影响。

2.1 实验数据及评价指标

2.1.1 数据集

Criteo 和 Avazu 是kaggle 平台上两个公开的广告数据集,近年来也成为广告点击量预测模型的基准评测数据集。Criteo 包含了4 500 万用户点击广告的数据样本,该数据集有26 个脱敏类别特征和13 个连续数值特征。Avazu 包含了4 000 万用户点击记录,有24 个特征字段。本文实验对两个数据集均采用8 ∶2 比例划分:即80%用于训练,20%用于测试。实验采用AUC和Logloss 作为评价指标[11-12]。

2.1.2 实验超参数设置

实验采用Tensor flow 实现了所有模型,Criteo 和Avazu 的嵌入向量的维度分别设置为16 和40,使用衰减学习率,初始值为0.1,衰减率为0.9,SENET 中的两个非线性全连接层使用Relu 作为激活函数,所用到的DNN 网络隐藏层节点数为512,Drop Out Ratio 为 0.5,使用Adam 作为优化器[13]。

2.2 对比实验模型设置

为了验证FIFM 单模型和融合DNN 网络的性能,本文将实验分为2 组,shallow 组和Deep 组,并且把基线对比模型分为两组。Shallow 组基线模型包括LR,FM,AFM,IFM。Deep 组基线模型包括Wide&Deep,Deep FM,DCN。对于Deep 组模型,所有模型统一设置激活函数为Relu,输出节点的激活函数为Sigmoid,优化器采用Adam。

2.3 FIFM 模型与基线模型性能对比

表1 和表2 给出了Shallow 组和Deep 组的对比模型在Criteo 和Avazu 两个数据集上性能表现。FIFM 相比LR,FM,AFM 和IFM 模型提升了3.3%,2%,1.5%,0.9%。在Deep 组并联融合了DNN 网络进行高阶特征后,Deep FIFM 同样优于其他对比模型。可见,对输入特征进行重要性加权处理,既可以实现特征的有效组合,同时也有利于让DNN 得到更充分的高阶组合特征信息。使得组合特征与实际目标特征更相近,提高了CTR 预测的准确率。

表1 Shallow 组模型的性能对比

表2 Deep 组模型的性能对比

2.4 超参数对模型性能的影响

如表3 所示,以8 步长,逐步调整Embedding 向量的大小,观察模型在两个数据集上的效果,可以看到当Embedding 大小为16 时,模型在Criteo 数据集表现最好;当Embedding 大小为40 时,模型在Avazu 数据集表现最好,此时,Embedding 向量能够较好地表示原始特征。所以,Ebedding 向量的大小并不是越大越好。

表3 嵌入向量维度对FIFM 性能影响

3 结语

本文从特征重要性的角度出发,将挤压提取网络和注意力机制应用到特征预处理中,能够根据不同的输入样例自适应地学习特征组合。通过聚合特征的全局信息,并从bit-wise 和vector-wise 不同的细粒度为特征计算权重,学习特征的动态感知因子。通过在两个真实数据集上验证模型的效果,证明FIFM 和Deep FIFM 的性能优于其他基线模型,提升了广告点击率预测的准确率。

本文主要从广告特征交叉的角度进行模型设计,但没有考虑到广告的位置信息以及用户历史交互行为信息。未来可以使用位置编码和长短时记忆网络处理这部分的特征信息,进一步提升模型性能。