基于单纯形积分的滑坡堆积体体积计算方法*
2022-06-23郭明珠梁洲婕王天成
郭明珠,梁洲婕,王天成,刘 晃
(北京工业大学 城市建设学部,北京 100124)
0 引言
由于特殊的气候、水文、地质等自然条件,西藏地区地质灾害频发,具有灾害类型多、影响范围广、破坏程度大等特点,其中滑坡、泥石流、崩塌产生的直接危害最为严重。滑坡的发生常会导致房屋倒塌、道路中断、河流堵塞,威胁下游水利工程建设,阻碍土地、矿产、水利等资源的开发利用(张梁等,1998;曹叔尤等,2013;郭明珠等,2021)。滑坡灾害危及群众生命财产安全,严重影响山区经济社会发展。灾害发生后,当务之急是进行灾后重建工作及灾害评估工作。准确测量滑坡堆积体体积,有利于灾后重建工作的开展,地质灾害评价工作的进行以及后期土地、矿产等资源的开发。
现有计算滑坡堆积体体积的几何方法主要有以下几种:一是将滑坡视作一个半椭球,代入半椭球体积公式计算滑坡体积(Cruden,Varnes,1996);二是基于积分近似计算原理,利用不规则形体体积的计算方法,手工绘制网格计算滑坡堆积体体积(熊道锟,胡济珍,1990);三是以统计关系计算为主,通过建立滑坡体体积和投影面积、滑坡体积与地震震级、滑坡体积与前期降水量、滑坡体积对数lg与滑坡最大垂直、水平距离、等效摩擦系数等经验公式计算滑坡堆积体体积(Malamuda,2004;Guzzetti,2008;李军,周成虎,2002;尉德新等,2019);四是用平行断面法计算滑坡堆积体体积,利用勘探剖面将地质体分为不同块段,分别计算并累加得到滑坡堆积体体积(王湘桂等,2012);五是对比滑坡前后数字高程模型,计算出滑坡堆积体的体积(殷跃平等,2011;张小咏等,2013;韩健楠,2018;Chen,2005);六是采用三维激光扫描仪或双目立体视觉技术获取滑坡堆积体的三维图像信息构造几何模型,以堆积体顶部顶点为三棱锥顶点、堆积体底面为三棱锥底面,自上而下将堆积体剖分成若干,计算滑坡堆积体体积(陈展鹏等,2013;于欢,2018)。
现有的几何计算堆积体体积主要是将堆积体拟合成多面体或拆分成三棱柱、三棱锥进行计算,计算方法较为繁琐。本文尝试将石根华(1997)提出的单纯形积分理论与Dlaunay三角剖分理论相结合,提出了一种新的计算堆积体体积的方法,以西藏昌都地区芒康县索多西乡的雪隆囊滑坡为例,通过Matlab的Dlaunay三角剖分算法将堆积体剖分成多个三棱锥代入单纯形积分理论进行计算。
1 研究区及滑坡堆积体概况
1.1 研究区概况
雪隆囊滑坡堆积体位于青藏高原东南缘金沙江上游的西藏昌都地区芒康县索多西乡雪隆囊村。滑坡区位于金沙江深切割区的峡谷之中,气候垂直变化显著,属于典型的高山峡谷地貌,山体庞大密集,山峰陡峻,两岸地势高差悬殊、地形起伏很大,相对高程在2 000 m以上,切割深度在800 m上下,两岸山体高程可达2 000~4 000 m。河谷干热、高山冷湿,属于典型的亚热带气候区,物理风化作用极其强烈。滑坡所在区域降雨稀少,多年平均值为497~620 mm,主要集中在5—9月,占全年的85%以上。滑坡区内裸地、荒山草坡居多,部分区域基岩出露,整体植被覆盖率低,不利于水土保持及斜坡稳定性,故该流域为滑坡易发区。滑坡所在位置的区域构造活动强烈,地形地貌复杂,属于我国一级阶梯与二级阶梯的过渡地带。滑坡所处的金沙江段,江水总体流向由N20°W转为N50°W,河谷深切,深度达700~1 000 m。同时,河谷狭长,水流湍急,坡降不明显。河流两岸冲刷痕迹明显,有河相沉积。
1.2 滑坡堆积体概况
雪隆囊滑坡堆积体位于苏洼龙坝址上游5.88 km岗达村对岸,前缘临江。由于堆积体前缘的阻隔,金沙江在此形成绕堆积体前缘的弧形河道,堆积体后缘及两侧均以干沟与山体相隔离,在地形上形似圈椅。
堆积体表面地形平缓,坡度一般为5°~20°,前缘直达江边,与河床覆盖层直接相接。堆积体中部为一低洼地带,将堆积体分成两级台阶状,临江部分顶面高程2 440~2 500 m,为堆积体I区;靠山侧顶面高程2 500~2 620 m,为堆积体II区。根据中国电建集团北京勘测设计研究院有限公司的地质勘察报告(以下简称“地质勘察报告”),绘制了雪隆囊滑坡剖面和平面图(图1、2)。
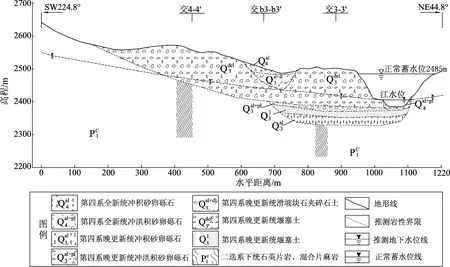
图1 雪隆囊滑坡剖面图(据地质勘察报告修改)Fig.1 Section of the Xuelongnang landslide(modified according to Geological Survey Report)

图2 雪隆囊滑坡平面图(据地质勘察报告修改)Fig.2 Plane of the Xuelongnang landslide(modified according to Geological Survey Report)
2 计算理论
2.1 单纯形积分理论
单纯形积分理论由美国数学力学家石根华(1997)提出,该方法可用边界顶角的坐标来计算块体体积和重心,其基本原理如下:
一般的维单纯形有+1个有序顶点,,,…,,表示为:
:(,,,…,0)
:(,,,…,1)
:(,,,…,2)
……
:(1,2,3,…,)
维坐标单纯形有+1个顶点,,,…,,表示为:
:(0,0,0,…,0)
:(1,0,0,…,0)
:(0,1,0,…,0)
……
:(0,0,0,…,1)
雅可比行列式为:
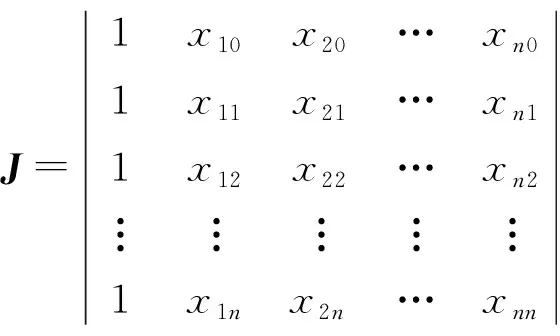
(1)
一个维单纯形积分为:

(2)
式中:表示的次数。
标准的三维积分式如下:

(3)

(4)
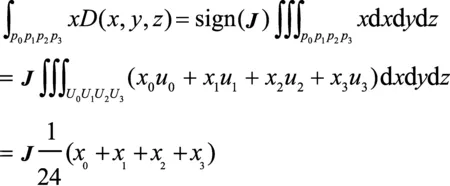
(5)
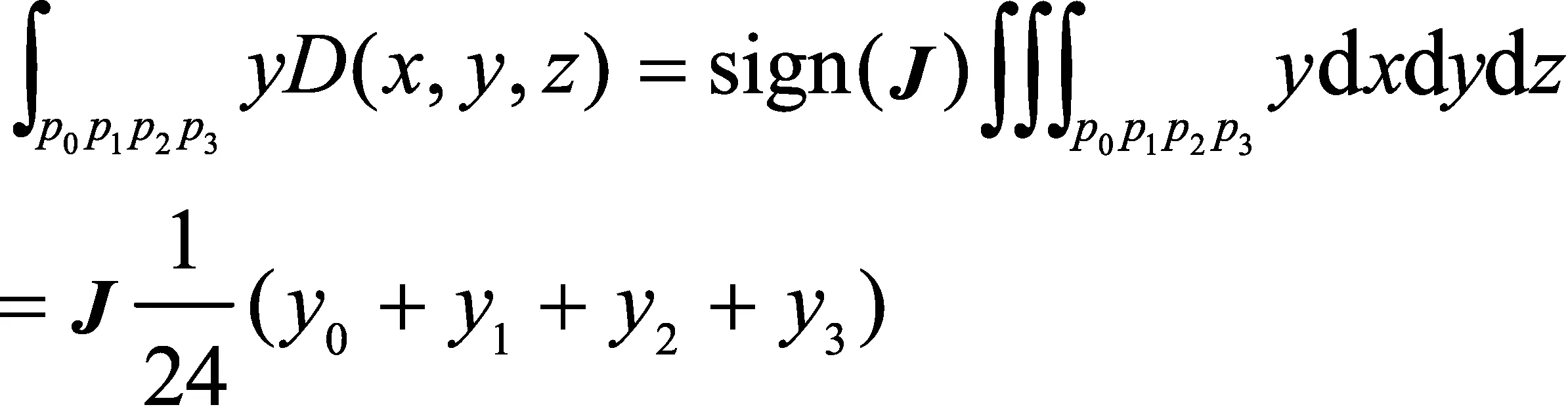
(6)

(7)
式中:表示点(=1,2,3,…,)的坐标;表示点(=1,2,3,…,)的坐标;表示点(=1,2,3,…,)的坐标。
2.2 Delauany三角剖分
令={,,…,}为平面域()上个离散点的集合,俄国数学家Dlaunay在1934年的相关研究证明:必定存在且仅存在一种三角剖分(一般称之为Delauany三角剖分)算法,使得所有三角形的最小内角之和最大。
一般情况下,一个完整的Voronio图应该由多个Voronio多边形组成,第个Voronio多边形的数学表达形式如下:
={∈:=-=≤=-==1,2,…,;≠,=1,2,…,}
(8)
式中:=-=表示平面域上点和节点之间的欧氏距离。
从式(8)可知,Voronio多边形内任意点到节点的距离比到点集中任何其他节点的距离更近。因此由节点和每个相邻节点的垂直平分线所形成的开式半平面的交集组成,所以,此时必为凸多边形。一般情况下,Voronio图的一个顶点同时属于3个Voronio多边形,每个Voronio多边形内有且仅有1个节点。连接3个共点Voronio多边形分别对应的3个节点则形成一个Delauany三角形,所有这样的三角形的集合就是著名的Delauany三角剖分(丁永祥等,1994)。
2.3 单纯形积分求重心及体积
根据数值流形方法的单纯形积分以及重心的定义,可得到体积、重心(武艳强等,2011)的表达式为:
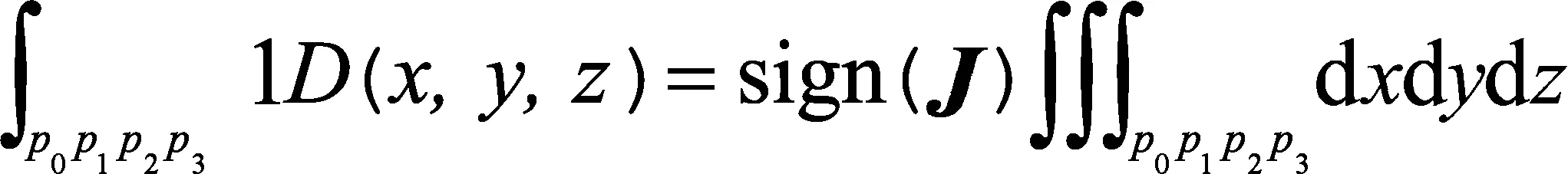
(9)
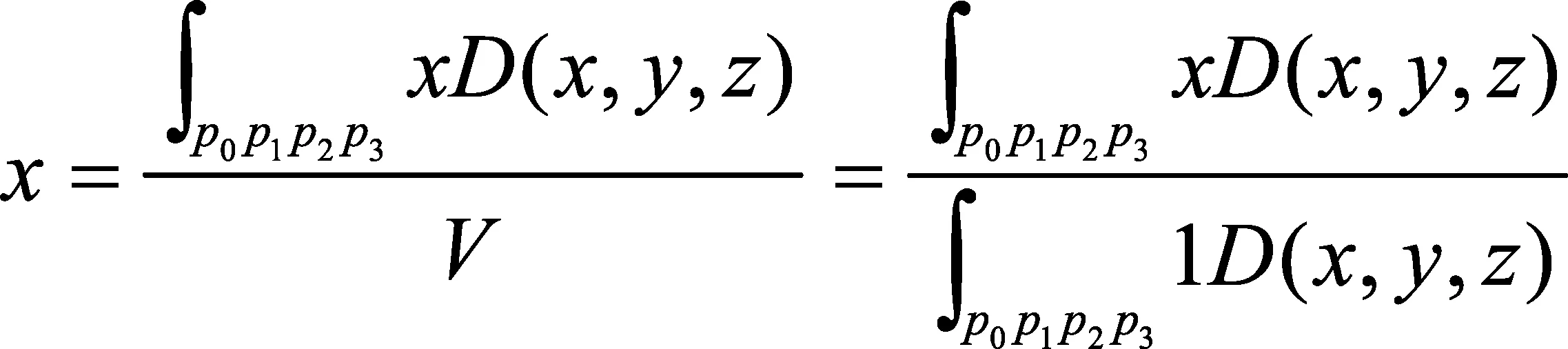
(10)
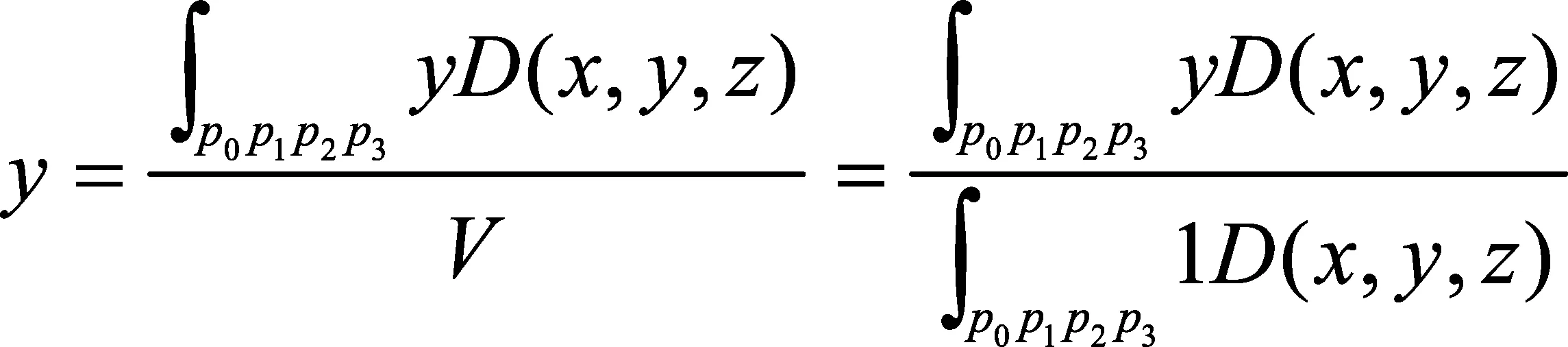
(11)
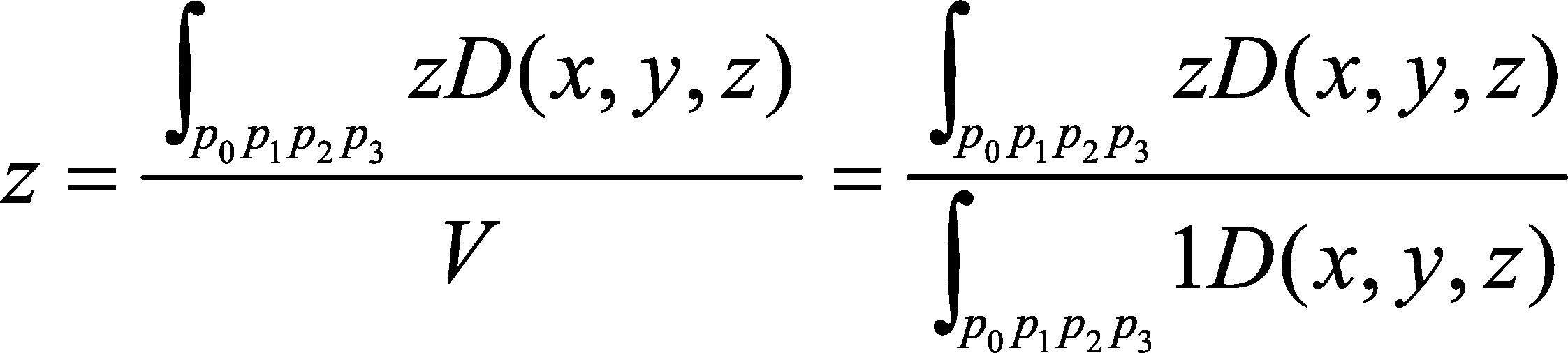
(12)
3 计算方法和结果
根据现场勘测获得滑坡后壁、滑坡周界、堆积体表面等关键位置的数据(如经纬度及高程),确定多个关键点(表1)。由于数据量过多,篇幅有限,表1仅给出部分关键点数据,其中、值由关键点的WGS84坐标转换西安80坐标得到。
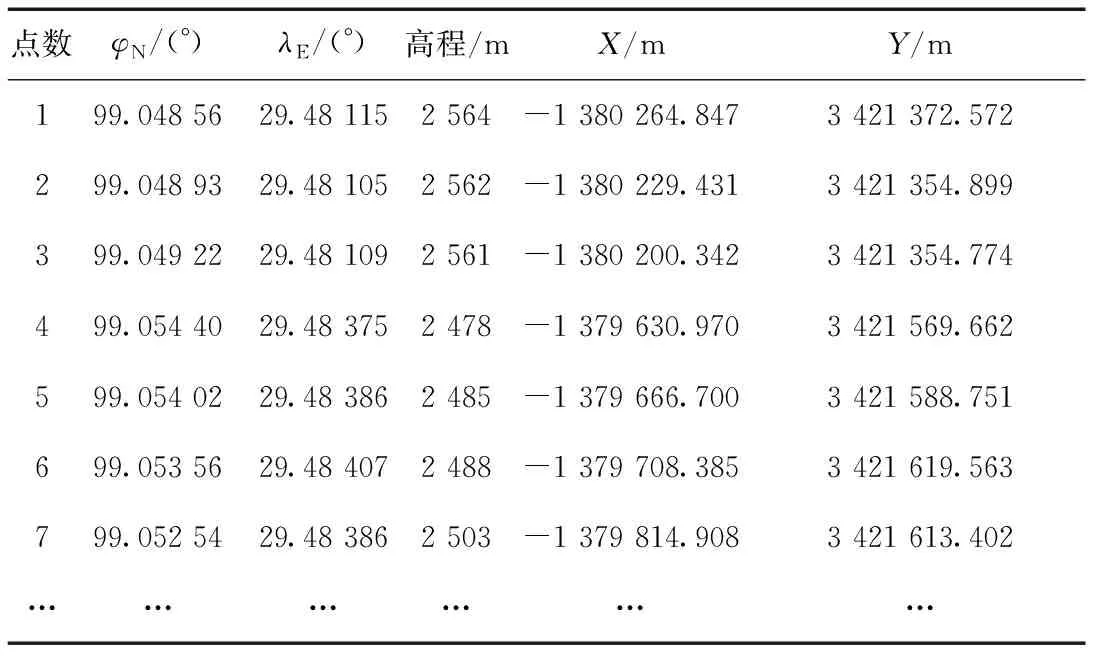
表1 关键点数据Tab.1 The data of some critical points
将关键点经纬度转换为大地坐标,使用Matlab的曲线拟合工具箱对关键点坐标进行拟合(图3),得出二元一次函数、二元二次函数和二元三次函数曲线拟合结果(表2)。由表2可知:①根据相关系数和均方根误差可知,二元三次曲面拟合效果最优,二元二次曲面次之,二元一次曲面较差;②滑动面拟合精度的提高依赖于勘察报告以及关键点的个数。
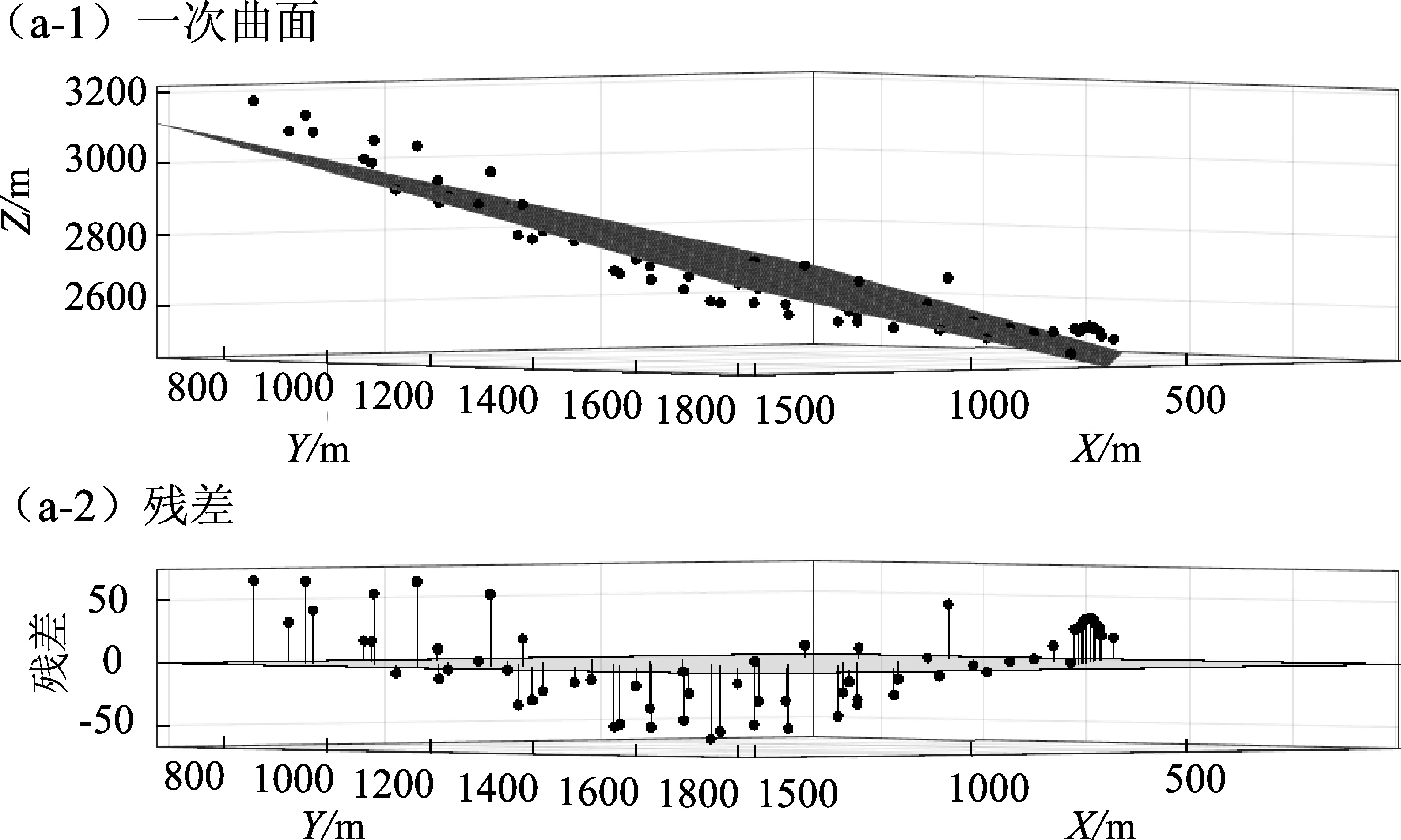
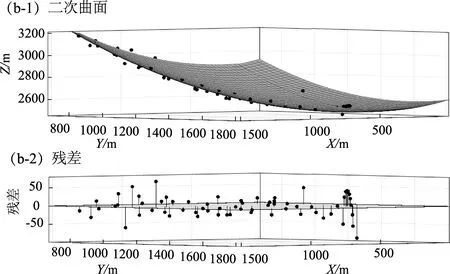
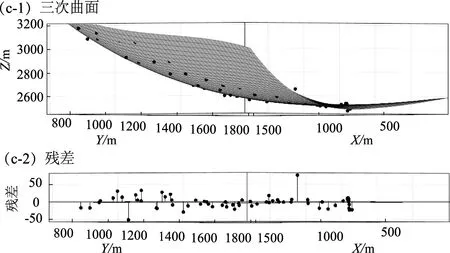
图3 滑动面模拟二元一次(a)、二次(b)、三次(c)曲面图及残差Fig.3 The sliding surface simulating binary primary(a),quadratic(b),and cubic(c)surface diagram and residuals

表2 滑动面曲线拟合结果Tab.2 Curve fitting of the sliding surface
结合地质勘察报告结果对拟合结果进行评价,选出最佳拟合滑动面曲线。根据拟合滑动面曲线算出滑动面计算点坐标,与堆积体表面数据结合,整理得出堆积体形状及其三维坐标。利用Matlab的三维Delauany三角剖分算法,将堆积体剖分成三棱锥(图4),并将三棱锥相对应的点坐标依次带入公式(1)、(3)进行计算,得到每个三棱锥体积,累加得到滑坡体体积。拟合计算程序如图5所示。

图4 三角剖分示意图Fig.4 Schematic diagram of triangulation
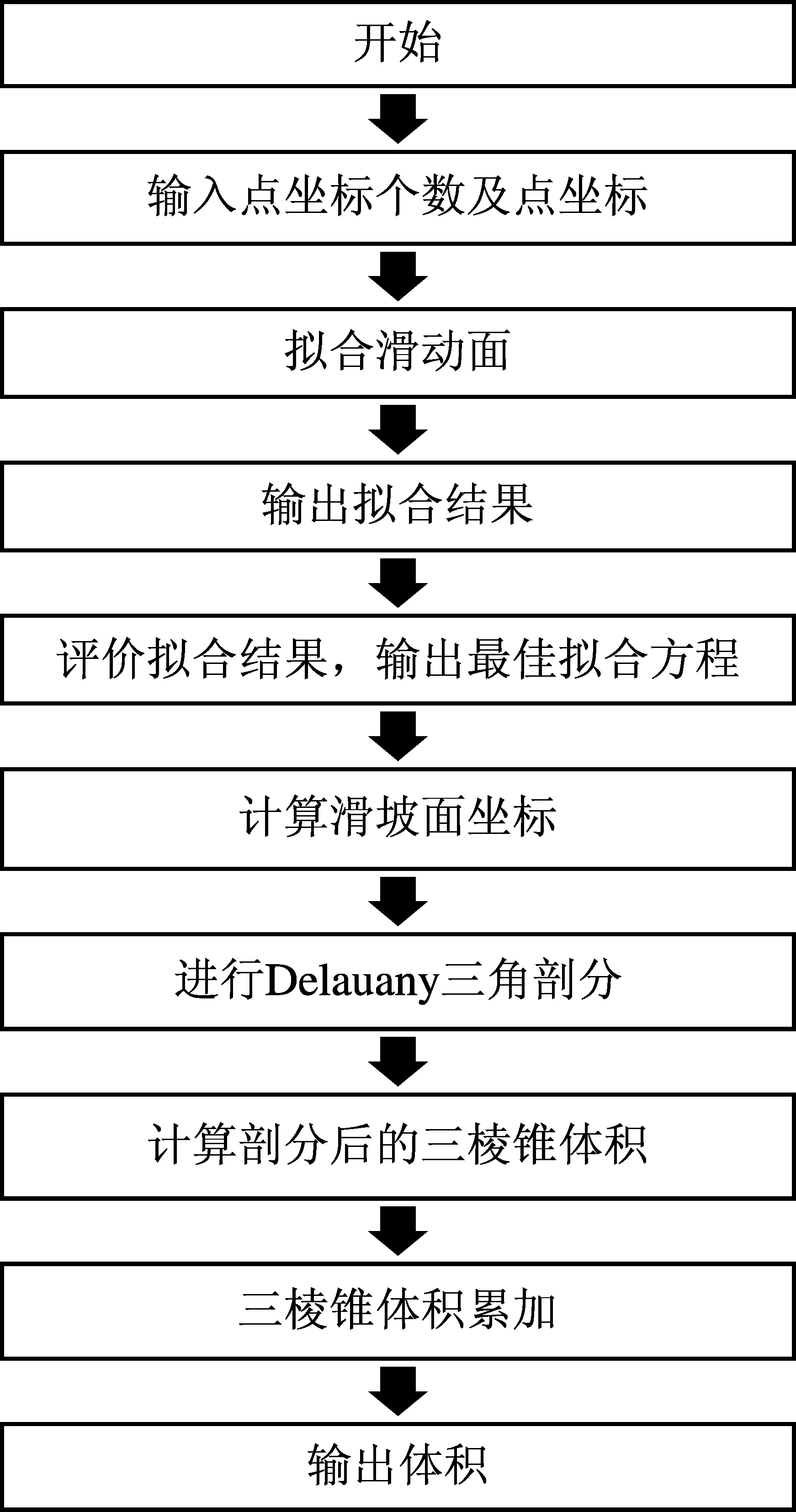
图5 滑坡堆积体体积计算程序图Fig.5 The flow chart of the landslide volume calculation
利用单纯形积分以及平行断面法、经验公式法分别计算堆积体体积,计算结果及具体计算公式见表3。由表3可知:

表3 不同方法得出的堆积体体积Tab.3 The volume of accumulation body obtained by different methods
(1)单纯形积分计算结果与地质勘察报告值对比,两者相差5.63%,吻合程度较好,说明该方法计算结果可信度较高。
(2)单纯形积分计算结果与传统几何方法计算结果相差27.4%。传统几何方法计算滑坡体积时将滑坡的滑动面当作椭球面,未考虑滑动面的实际情况;同时将滑坡体看作椭球形,对滑坡形态过度简化,未考虑不同滑坡之间的差异性。
(3)单纯形积分计算结果与经验公式法相比,分别相差5.2%、17.9%、75.3%。由于经验公式法选取的地域、样本类型、样本个数等都不相同,不同经验公式得出的结果相差较大。经验公式法具有明显区域性,不适用于所有滑坡堆积体体积计算。
(4)其他学者(陈松,2016;陈剑,崔之久,2015)对此滑坡体进行计算,得到滑坡体体积为4.1×10m,本文方法计算结果与其相差15.9%。
(5)单纯形积分计算方法精确度与关键点的个数、野外实地勘查的详细程度以及构建几何模型的精确程度相关。关键点个数越多,构建的滑坡体几何模型越贴近实际,计算结果越准确。
4 结论
本文利用Matlab软件对滑动面曲线进行拟合得出完整堆积体,将滑坡堆积体剖分成三棱锥,利用单纯形积分计算堆积体体积。得出结论如下:
(1)相较于其它方法,单纯形积分计算方法准确度较高,可用于滑坡堆积体体积的计算。
(2)结合Delauany三角剖分算法,将任意多面体剖分成三棱锥并代入单纯形积分进行计算的方法可用于双目立体视觉技术或三维激光扫描技术建立滑坡堆积体几何模型后的滑坡体体积计算,同时还可用于任意不规则形体体积计算。
(3)基于Matlab现有的视觉图像识别处理技术,凹陷块体的外部边界无法准确识别,计算凹陷块体体积时需考虑缺失部分,计算后进行相应删减。
感谢中国电建集团北京勘测设计研究院有限公司提供雪隆囊滑坡堆积体(岗达堆积体)的勘探资料和体积估算。
