矩形隧道结构的地震动力破坏研究*
2022-06-23魏晓刚刘会丽杨柳川王占阳李广慧刘书贤法靖宇
魏晓刚,刘会丽,杨柳川,王占阳,李广慧,刘书贤,法靖宇
(1.郑州航空工业管理学院 土木建筑学院,河南 郑州 450046;2.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;3.郑州意和达建筑科技研究院,河南 郑州 450046;4.中建七局安装工程有限公司 河南 郑州 450046;5.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000)
0 引言
随着城市建设的飞速发展,交通问题成为制约城市发展的“瓶颈”。对城市地下空间的合理开发是缓解城市交通问题的关键手段之一,因此,对于地下结构的建造和发展备受关注。我国地震频发,地下结构造价高、破坏后难以修复。因此,地下结构的安全问题是不可回避的,设计水准需要提高,对地震荷载作用下隧道结构的动力破坏的研究就显得尤为重要(张伟,2009)。
近年来国内外学者对地下结构抗震开展了大量的研究。朱星宇和张志强(2021)依托乌鲁木齐轨道交通2号线工程,采用有限元差分法探讨了地震作用下隧道下部结构及道床的作用特性;王志伟(2021)运用ANSYS有限元软件建立数值模型,研究了地震作用下不同参数对隧道结构内力和位移的影响,并在此基础上对比分析了不同减震措施的减震效果;陈艺丹(2010)依托于重庆某铁路隧道,研究了软弱夹层处隧道结构衬砌的地震动力响应规律;Niu等(2017)通过振动台模型实验与土质边坡动态数值模拟对比分析的方法,探究了小间距隧道岩质边坡在地震作用下的动力特性及隧道结构的影响;Yang 等(2021)采用振动台实验研究了平行重叠隧道在地震作用下的动力响应和破坏特性。本文在隧道结构地震动力响应理论分析的基础上,采用数值模拟计算与振动台实验相对比的方法,探讨地震作用下隧道结构的动力破坏模式,以期为地下隧道结构的动力失稳破坏提供参考和借鉴。
1 地震作用下隧道结构动力响应的理论分析
当发生动力扰动(地震荷载、机械扰动或矿震)时,在静力与动力荷载联合作用下(何满潮,钱七虎,2010;魏晓刚等,2016),土-隧道结构复合结构体系的动力学方程为:
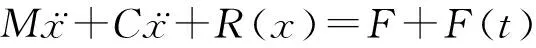
(1)
式中:为土-隧道结构组成的复合体的质量;为土-隧道结构组成的复合体所承受的静力荷载外力的合力;为在外力荷载作用下,土-隧道结构组成的复合体所产生的变形位移;()为地震荷载;()为土-隧道结构的抗力。令为土-隧道结构的弹性抗力系数,在外力扰动作用下,处于弹性变化阶段时,()=。
在动力荷载的扰动作用下(地震、岩爆、煤与瓦斯突出等),土-隧道结构在水平方向(方向)上会产生一定的位移。假设在动力荷载作用下土-隧道结构所产生的应力为,应变为,位移为。应力波在传播过程中的波动方程为:

(2)
式中:为扰动荷载应力波的传播速度,单位为m/s;令′=-为扰动荷载应力波引起的位移变化。
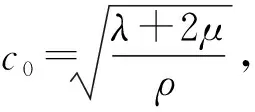
对式(2)进行求解变换可以得到:
′(,)=(-)+(+)
(3)
式中:(-)为应力波入射纵波的波动方程;(+)为应力波反射纵波的波动方程。
联立公式(1)~(3)可得到:
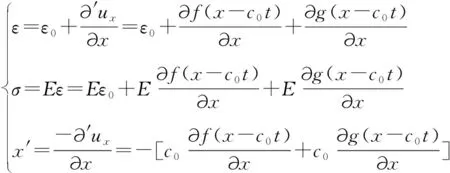
(4)
基于式(4),可以求得在应力波的作用下隧道结构内部的应力、应变、位移响应的数值解,从而可以较好地判断隧道结构的动力稳定性。
2 大型振动台模拟隧道结构动力破坏的实验研究
在现有的隧道结构动力破坏机理研究中,地下结构的动力模型实验较少,隧道地震破坏的实测数据尤其少。地下结构地震反应的振动台实验比离心机实验更可行。因此,笔者通过设计矩形截面的隧道结构的振动台实验,以期获得能够真实反映其破坏机理的实验数据。
2.1 振动台实验的物理参数
隧道结构的振动台实验在辽宁工程技术大学实验室进行,采用电液伺服振动台,其台面几何尺寸为3 m×3 m,额定承载为10 t,运动方向为水平双向,水平向最大加速度为1.5 g,加载频率为0~50 Hz,可以快速定义和控制不同的脉冲振动波形进行加载实验。
隧道结构的振动台实验模型如图1所示。实验选取刚性模型箱,尺寸为2 m×2 m×1.5 m(长×宽×高),为减小边界效应,在模型箱与模型之间均设置20 cm厚的聚苯乙烯泡沫板和一层塑料薄膜。

图1 振动台及实验模型箱Fig.1 Shaking table and experimental box model
2.2 隧道结构模型的相似比设计
相似理论是隧道结构振动台实验的理论基础。基于相似原理,模型实验的结果可以与原型结构建立直接的物理数据关系,从而能够推断出原型结构的抗震性能和破坏机理(夏颂佑等,1980)。本次实验以Buckingham π定理(顾大钊,1995)为基础进行相似体系设计,从动力量纲分析入手,选择长度、弹性模量和密度为模型结构的基本物理量,计算得到其它物理量满足的相似关系,见表1。
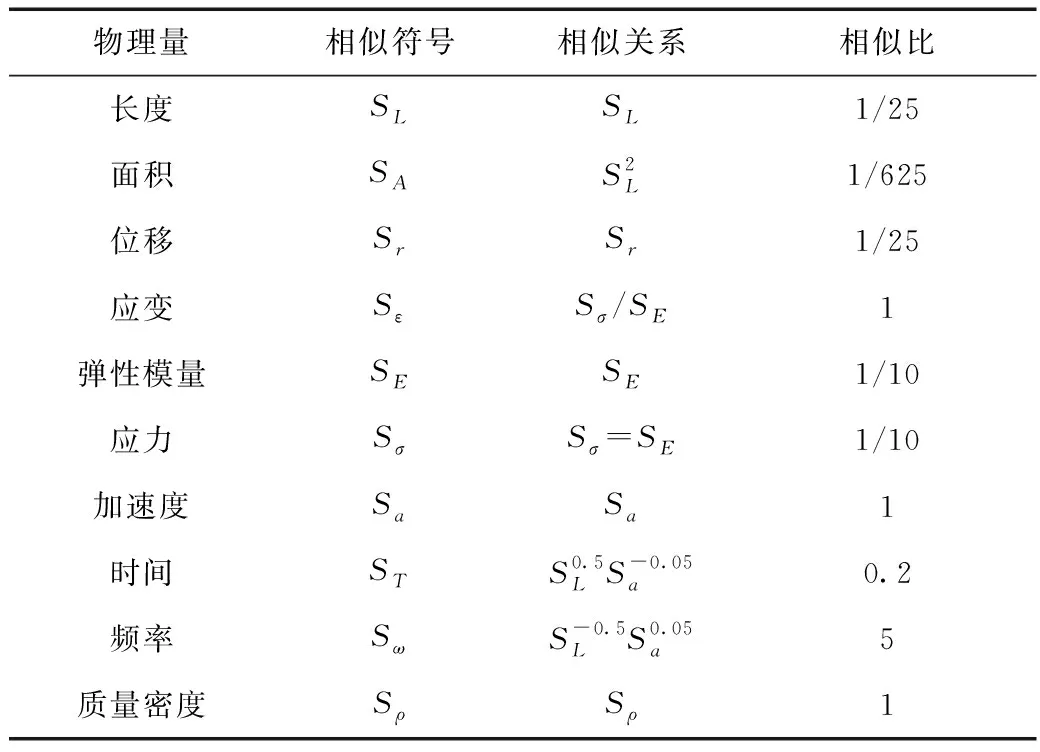
表1 模型主要相似参数Tab.1 The main similar parameters of the model
2.3 隧道结构模型的制备及传感器布设
魏晓刚等(2021)基于有限元软件ANSYS/LS-DYNA分析了地震作用下地下结构的失稳破坏机制,发现圆形截面的地下结构的抗震性能较好,拱形截面次之,矩形截面最差。为了验证前期数值模拟计算结果的可靠性,基于最不利工况的原则,此次振动台实验中所研究的隧道结构截面形式为矩形截面。振动台实验中隧道结构的整体模型几何尺寸为1.6 m×1.6 m×1.3 m(长×宽×高),其中矩形隧道尺寸为300 mm×196 mm×700 mm(长×宽×高)。
隧道结构的缩尺实验材料选择有机玻璃,其衬砌厚度为20 mm;土层采用细砂来代替;隧道的振动台实验需要测定结构内部的反应加速度、土压力及应变,选用的传感器主要有加速度传感器、土压力计及应变片,各传感器的布设位置如图2所示。
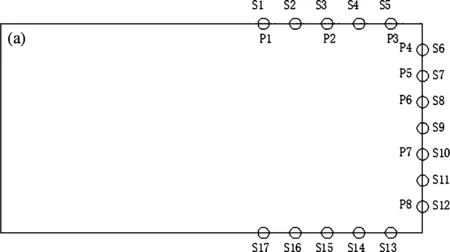

图2 土压力计及应变片(a)和加速度传感器(b)位置布置(单位:mm)Fig.2 Earth pressure and strain gauges(a)and accelerometers(b) layout(unit:mm)
2.4 地震波的选取与加载
由《建筑结构抗震设计规范》(2016年版)(GB 50011—2010)、《城市轨道交通结构抗震设计规范》(GB 50909—2014)、《地下结构抗震设计规范》(GB/T 51336—2018)可知,在对工程结构进行抗震性能分析时,地震波的选取应遵循以下原则:地震波的持续时间应包含地震波振动最强烈的部分,一般为工程结构基本自振周期的5~10倍;持续时间的选择,根据是否进行弹塑性分析而确定。
基于土-隧道结构整体的自振周期以及相关规范的要求,实验中选取了ChiChi波、Loma波及Taft波3种地震波作为振动台实验的输入波。振动台的台面输入的加速度峰值逐级增加,分别为0.1、0.2、0.3、0.4、0.5、0.6 g,峰值加速度为0.1 g时3种地震波的地震动加速度时程曲线及傅氏谱如图3所示。
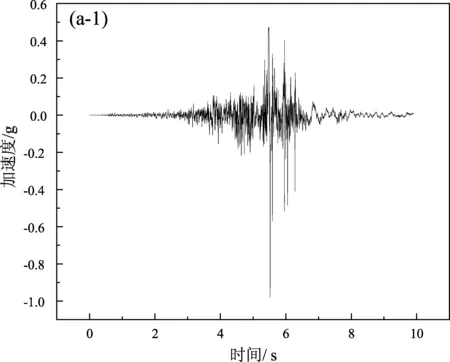
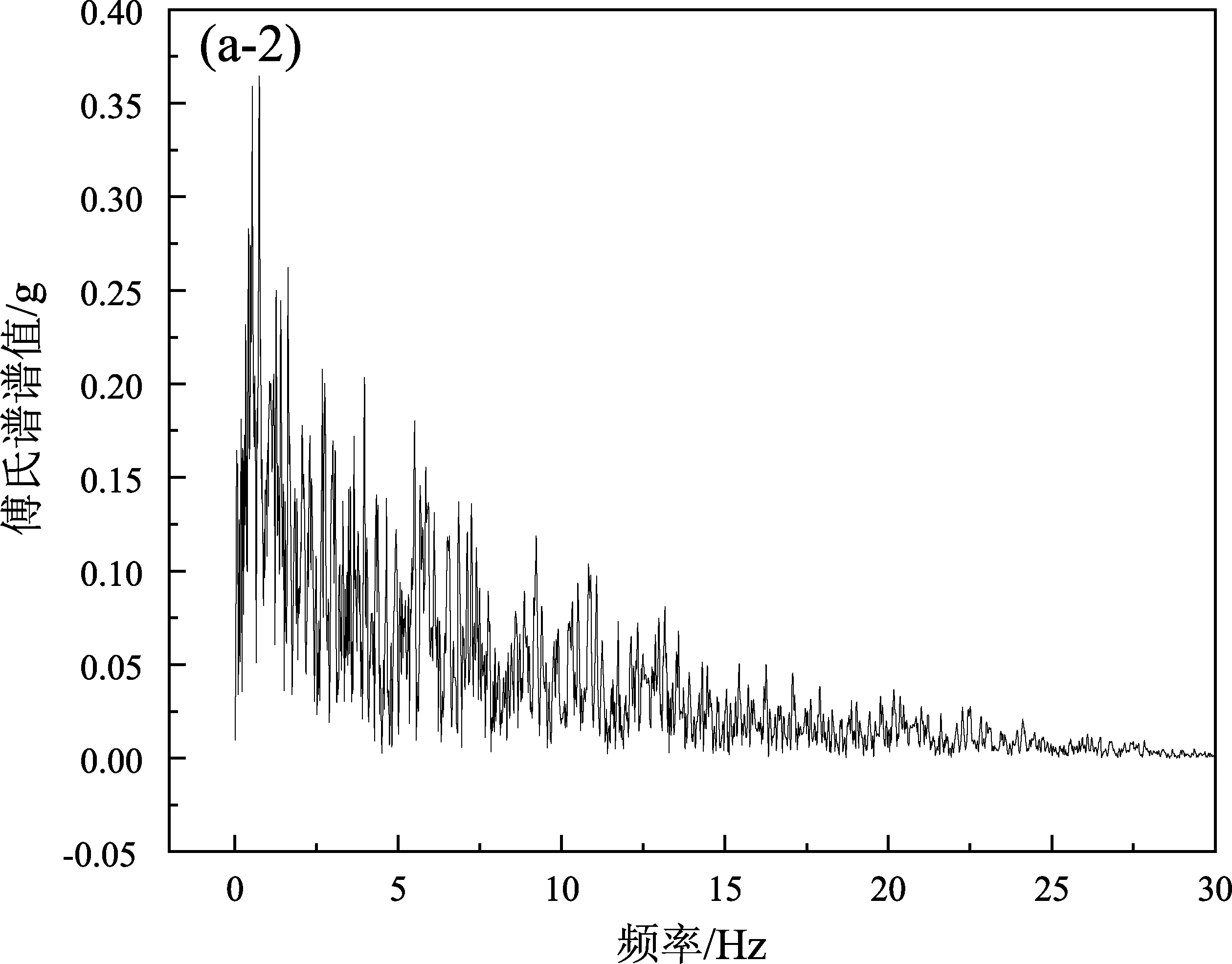


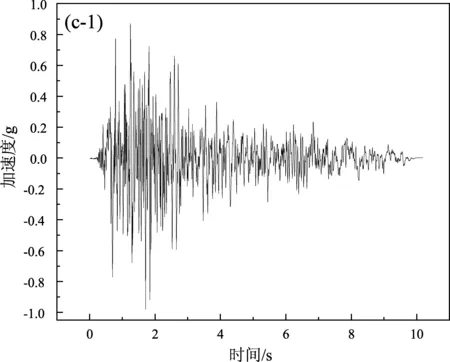

图3 ChiChi波(a)、Loma波(b)、Taft波(c)的加速度时程及傅氏谱Fig.3 Acceleration time history of ChiChi wave(a),Loma wave(b), and Taft wave(c)and their Fourier spectrum
实验采用单向(水平横向)输入激励,输入波的时间间隔和加速度峰值根据相似关系作了调整,实验时采用的步长是0.001 25 s。在开始激振前用小振幅的白噪声预振,使土体模型密实。然后每次改变加速度输入峰值时均输入白噪声扫描,以观测体系模型动力特性的改变情况。隧道模型的加载工况见表2。
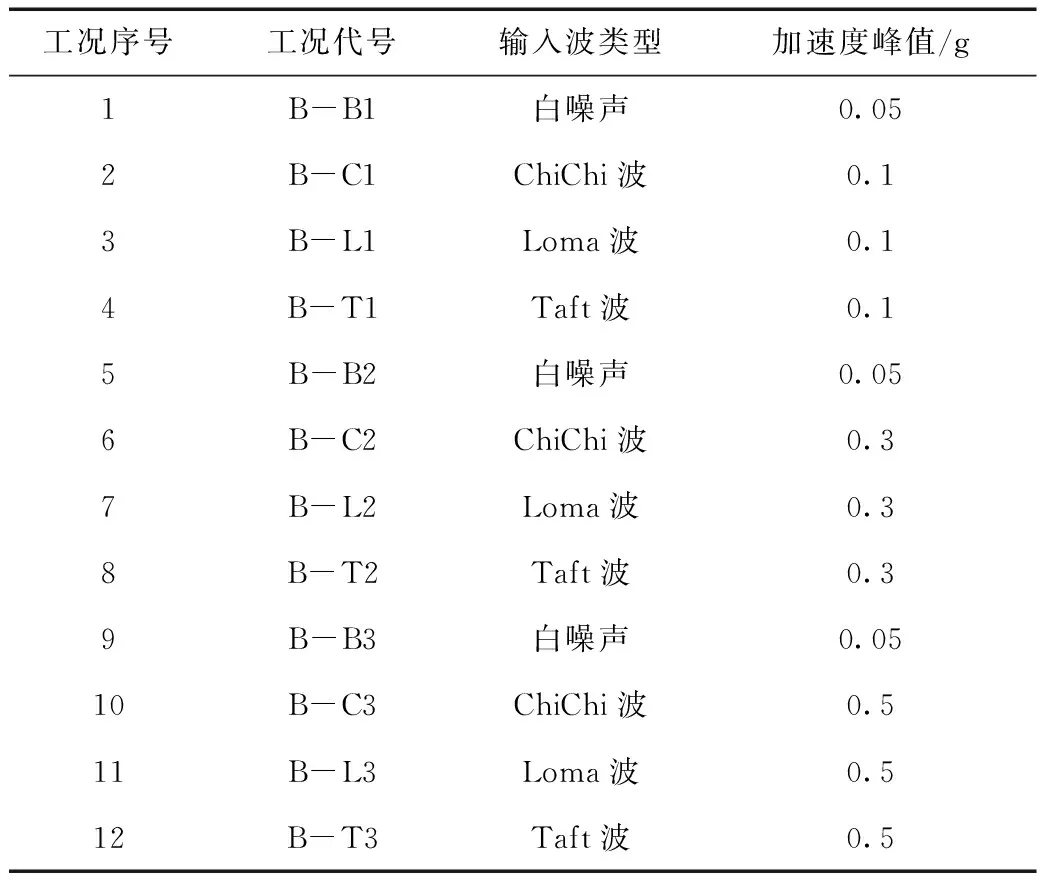
表2 隧道结构实验的加载工况Tab.2 Loading condition of tunnel structure experiment
2.5 隧道结构振动台实验结果分析
2.5.1 土-隧道结构整体实验模型的自振频率
测试系统自振频率的方法有很多(尚守平等,2006;Cristina,2013),本文根据实验加载方法,在实验每个工况开始之前分别采用幅值为0.05 g的白噪声对模型体系进行扫描,利用模型钢箱上的加速度传感器的频域传递函数求得模型体系的自振频率,各种工况下的自振频率的前3阶振型见表3。由表可知,随着实验工况的逐级加载,模型体系自振频率逐渐降低。
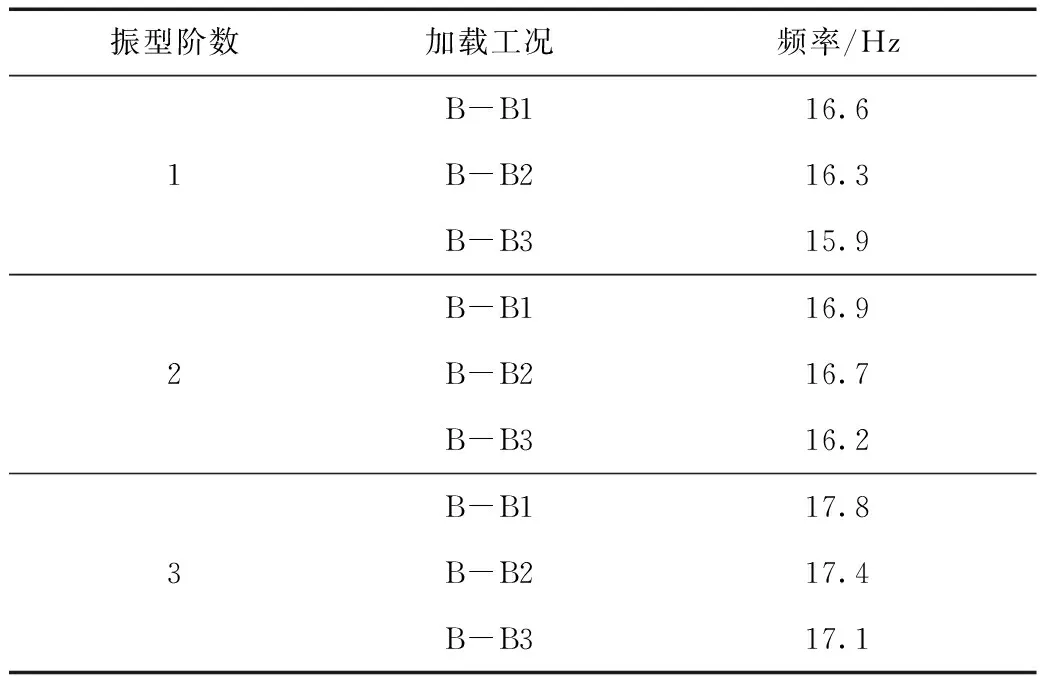
表3 模型体系的自振频率Tab.3 Natural frequency of model system
2.5.2 隧道结构的加速度放大系数分析
各种工况下隧道结构上各测点的加速度放大系数见表4。从表中可以看出,在各种工况下,隧道结构上各测点的峰值加速度均明显大于台面输入的峰值加速度,说明ChiChi波、Taft波和Loma波这3种地震波均对隧道各测点的加速度有放大作用。当输入的地震波峰值加速度为0.1 g时,对于隧道结构各测点的峰值加速度的放大作用最大,其次是0.3 g的输入波,最小的是0.5 g的输入波,即加速度放大系数随着输入加速度峰值的增加呈现逐渐减小的趋势,说明输入地震波的卓越频率与模型体系的基频越接近,土体的反应越大。比较这3种地震波,ChiChi波对隧道各测点的加速度放大作用明显大于其它两种地震波,Loma波作用下隧道各测点的峰值加速度最接近于台面输入的峰值加速度。

表4 各种工况下隧道结构各测点加速度反应放大系数Tab.4 Amplification coefficient of acceleration response at each measuring point of tunnel under working conditions
2.5.3 隧道结构的应变分析
在隧道结构模型的中心截面外表面上分别布置了17个应变片,布置如图2a所示(S1~S17)。图4给出了各种工况下各测点的应变峰值变化规律。

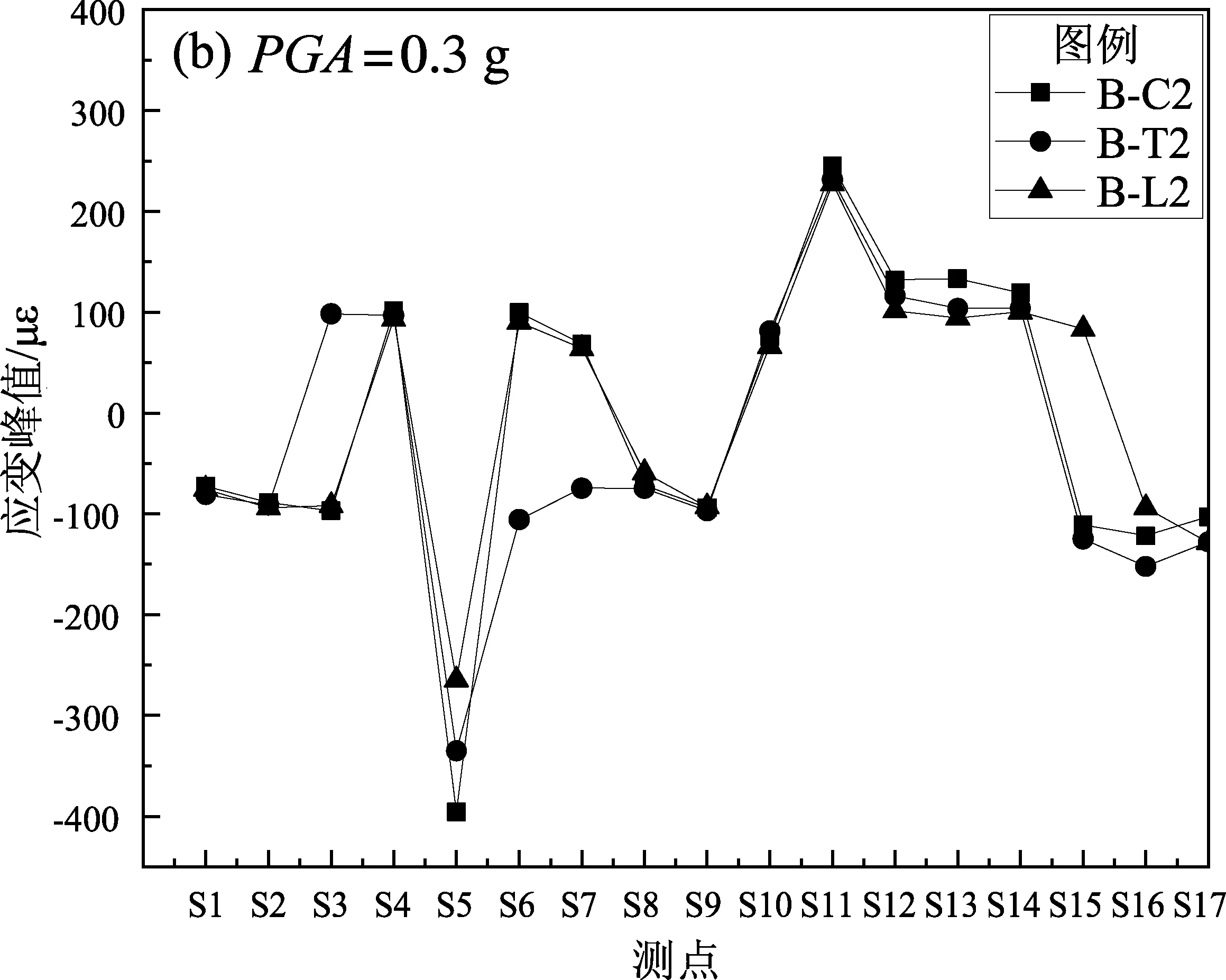
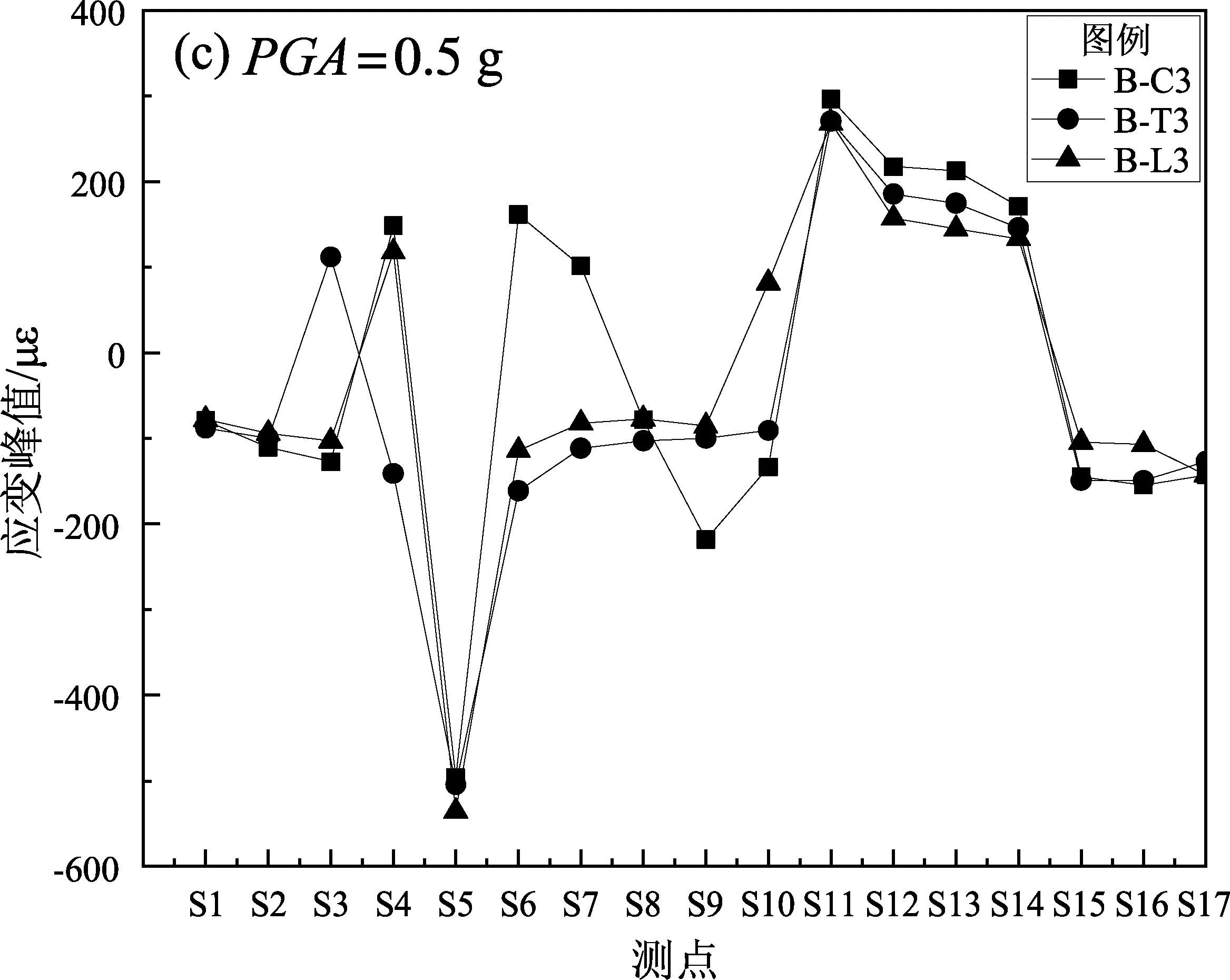
图4 各种工况下各测点的应变峰值Fig.4 Peak strains of each measuring point under working conditions
经过对比发现,在ChiChi波、Taft波与Loma波3种地震波作用下,选取峰值加速度为0.1 g、0.3 g和0.5 g作为输入波,各测点的应变峰值最大点均位于S5和S11处,说明在各种工况下矩形隧道测点S5和S11处应变最大,即矩形隧道的肩部最薄弱,在遭受地震荷载作用时最容易遭受变形甚至破坏;随着输入波的峰值加速度的增大,各测点应变峰值逐渐增大,说明矩形隧道的肩部为薄弱位置,强震作用下可能会诱发隧道结构的整体失稳破坏。
2.5.4 土-隧道结构模型的土压力分析
在隧道结构模型的中心截面上分别布置了8个土压力计,如图2a所示(P1~P8),其中测点P1~P3设置在矩形隧道上表面,在矩形隧道的侧壁沿不同埋置深度设置了P4~P8共5个测点。相较于矩形隧道侧壁的5个测点,隧道结构上表面的土压力较小,因此本文主要针对隧道结构侧壁的5个不同埋置深度的测点进行研究。
根据图5可知,在ChiChi波、Taft波与Loma波3种地震波作用下,选取不同峰值加速度作为输入波时,3种地震波的土压力峰值变化规律相似,即隧道中间部位的土压力值明显大于上下部位,说明隧道结构中部受到的土压力最大,也最易遭受到破坏。随着台面输入地震波的峰值加速度的增大,土压力峰值也随之逐渐增大,说明强震作用下矩形隧道承受的动土压力更大,结构的安全稳定性能就不容易得到保证,需要密切关注隧道结构的抗震承载能力。


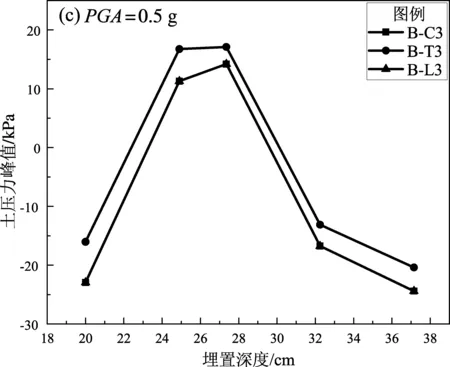
图5 各种工况下测点P4~P8的土压力峰值Fig.5 Peak values of the earth pressure at measuring points P4-P8 under working conditions
3 地震作用下隧道结构动力响应数值模拟
为了深入分析地震作用下隧道结构的动力响应,本文基于有限元软件ABAQUS进行数值模拟分析,采用非线性的莫尔-库伦本构模型进行数值模型计算,单元类型采用C3D8R。莫尔-库伦强度理论需要满足以下假设条件(孙海峰,2011;俞茂宏等,2011):①在岩土材料所承受的应力较小时,假设岩土类材料是各向同性的,并且满足理想化的线弹性的模型;②岩土类材料发生硬化时,假设其硬化条件为各向同性的粘聚硬化;③当岩土类材料进入强化阶段时,假设其满足柯西应力和逻辑应变的性质。
使用莫尔-库伦本构有以下几点局限性:①需与线弹性模型联合使用;②可通过改变粘聚力或等效塑性应变的方式,实现材料硬化功能和软化功能;③剪胀角和摩擦角的取值不可相同,否则在剪切破坏过程中会出现无限制的体积膨胀情况;④粘聚力不可为零,砂土等材料需将粘聚力设置为一较小数值。
为了更好地对比分析振动台实验与有限元数值模拟的差异性,本文所建立的有限元分析模型的边界条件及尺寸与振动台实验一致。模型底部采用固定边界,侧边界在水平方向可自由变形,模型部件的主要材料参数见表5。模型土长1.6 m(激振方向)、宽1.6 m、深1.3 m,采用实体单元对模型土和隧道结构进行网格划分,如图6所示。


图6 模型土(a)及随道结构(b)三维有限元模型网格划分Fig.6 Meshing of the soil model(a)and the tunnel sturcture model(b)with the 3D finite element model
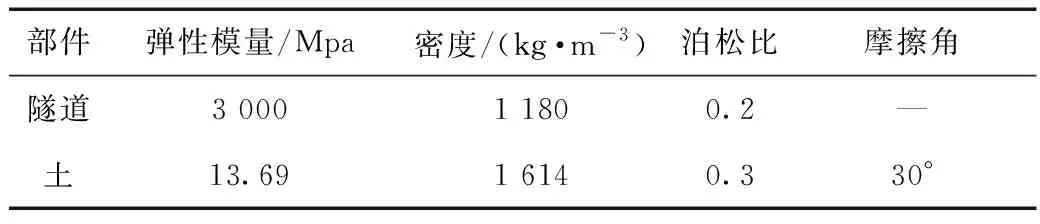
表5 模型部件的物理力学参数Tab.5 Physical mechanical properties of model components
本次模拟实验与振动台一样,选取3种地震波作为模型的输入波,分别为ChiChi波、Loma波和Taft波,每种地震波选取3种不同的峰值加速度,分别为0.1 g、0.3 g、0.5 g。为模拟实验振动台方向上的震动效果,对侧边边界自由度进行约束,在模型底部方向输入不同峰值加速度的地震波。
4 隧道结构地震动力破坏的数值计算与实验结果对比分析
4.1 加速度时程及峰值对比
由图7可知,矩形隧道上不同位置的4个测点处模拟与实验的加速度时程变化规律较为相似,各测点的加速度时程的强震段持时基本相同,其加速度峰值稍有差异但是浮动不大。其具体情况见表6。由表6可知,A4与A7测点处的峰值加速度模拟值略大于实验值,而A10与A13测点的峰值加速度模拟值略小于实验值。在隧道的垂直方向上,各测点的峰值加速度随着隧道的埋深增加逐渐减小,但是减小的幅度不太明显。位于矩形隧道腰部的A10测点的峰值加速度最小,位于矩形隧道右肩处的A13测点的峰值加速度最大。

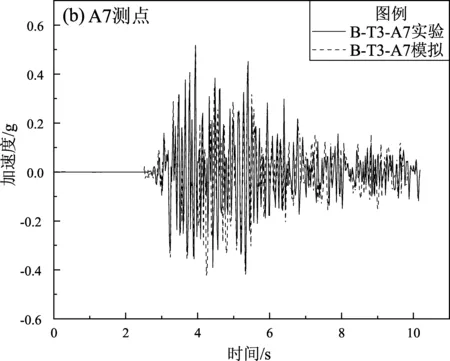

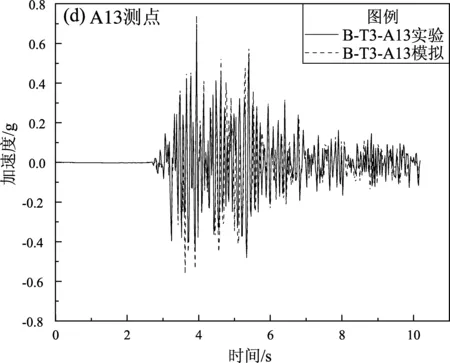
图7 工况B-T3下隧道各测点数值模拟与振动台实验加速度时程对比Fig.7 Comparison of acceleration time histories by numerical simulation and shaking table experiment at each point of the tunnel under B-T3 condition
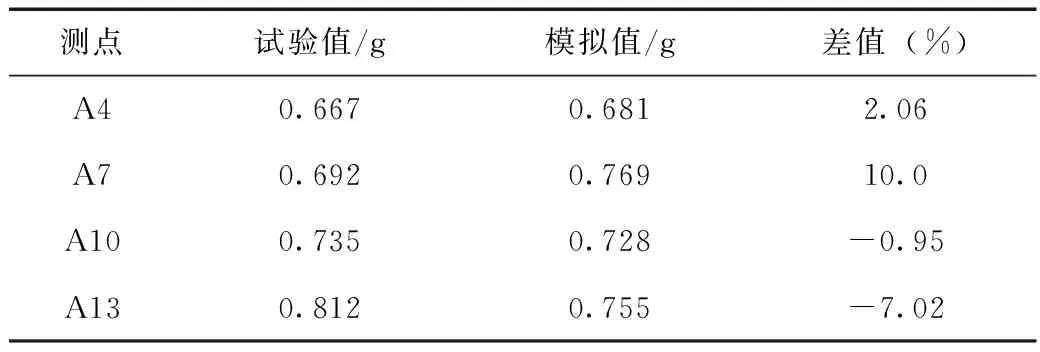
表6 隧道结构的实验与数值模拟加速度峰值对比Tab.6 Comparison of peak acceleration of tunnel structure between test and numerical simulation
4.2 加速度频谱特性对比
为了进一步对比有限元模拟与振动台实验的差异,使用SeismoSignal软件对加速度时程进行处理,得到各测点处数值模拟与振动台实验的傅氏谱对比图(图8)。由图8可看出:各测点数值模拟和振动台实验的傅氏谱变化规律基本相同,频率主要分布在0~10 Hz,说明土层由于滤波作用,对高频波产生了过滤作用,对低频波产生了放大作用。

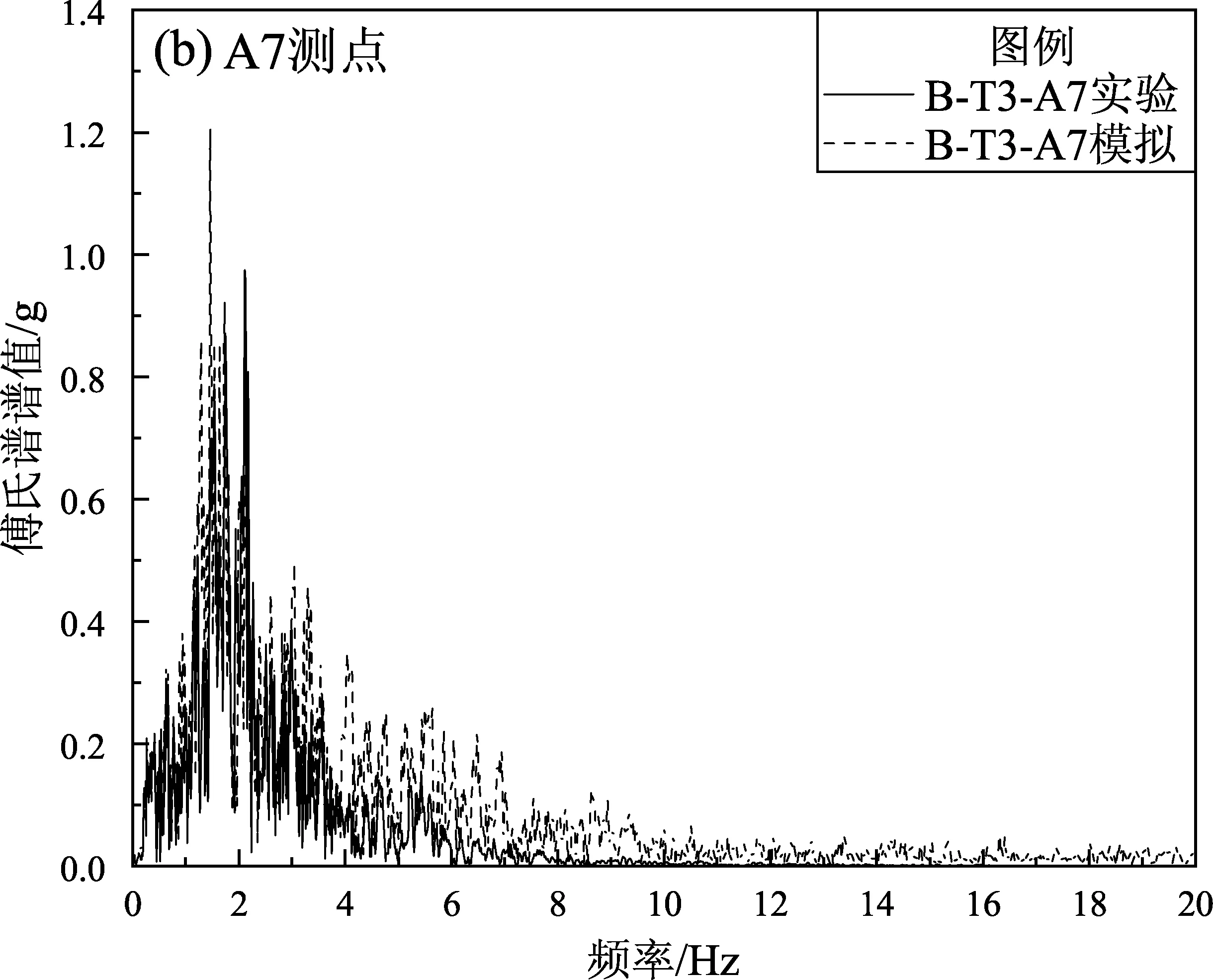

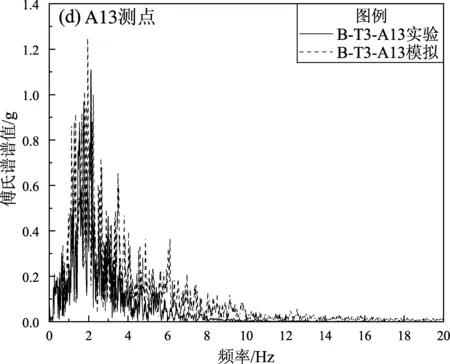
图8 工况B-T3下隧道各测点数值模拟与振动台实验傅氏谱对比Fig.8 Comparison of the Fourier spectrum by numerical simulation and shaking table experiment at each point of the tunnel under B-T3 condition
4.3 应力云图分析
根据有限元数值计算结果,得到不同工况下隧道结构的应力变化云图(图9)。由图9可见,3种工况下隧道结构的应力均在矩形结构的4个角处达到峰值,这4个角为隧道的薄弱部位。通过对比发现:虽然输入的地震波的峰值加速度均为0.5 g,但随着输入波形的不同,隧道的应力云图略有变化。Taft波与Loma波作用下,应力云图显示出矩形隧道的4个角应力最大,并且下面的两个角的应力比上面的两个角应力略大;而在ChiChi波作用下,矩形隧道结构的4个角的应力同样是最大,但左边上、下两个角的应力明显比右边的大。从应力峰值来说,Taft波最大,Loma次之,ChiChi波最小,但三者差异并不大。

(a)工况B-T3

(b)工况B-L3

(c)工况B-C3图9 各种工况下隧道结构的应力云图Fig.9 The stress nephogram of the tunnel structure under working conditions
4.4 位移响应分析
根据有限元数值模拟分析,得到各种工况下隧道结构各个部位的向水平位峰值图(图10)。如图10所示,在3种工况下,矩形隧道的位移峰值均位于左、右拱下角与底板处,其中底板位移略大一点,三者差别很小,其次是左、右拱腰处。3种工况下位移的变化规律基本相同,随着工况的不同,位移的大小略有不同,其中,Taft波作用下隧道结构的位移最大,Loma波次之,ChiChi波最小。3种波形作用下顶板与底板的位移差变化不大。隧道结构的位移越大,越不利于维持其动力稳定。
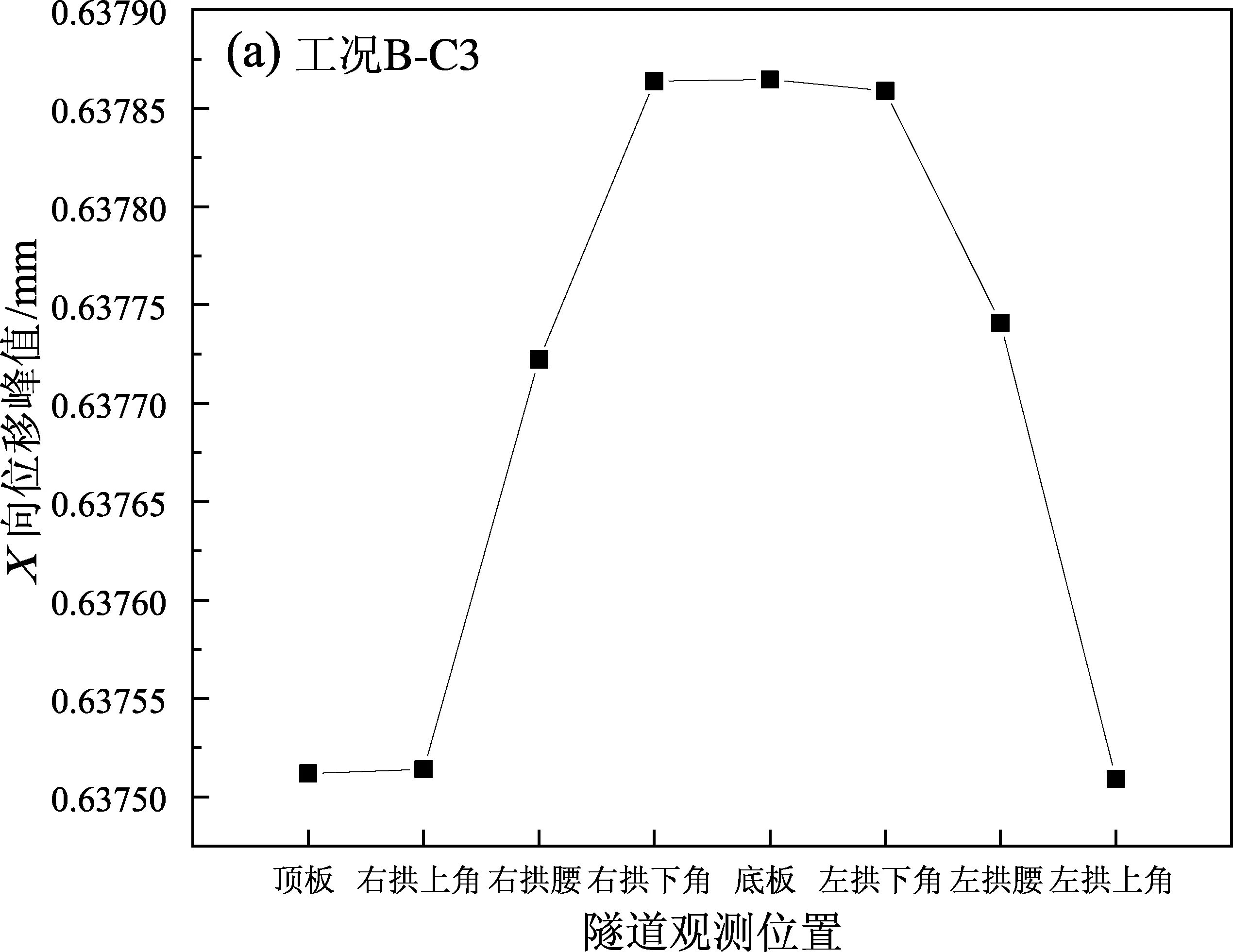
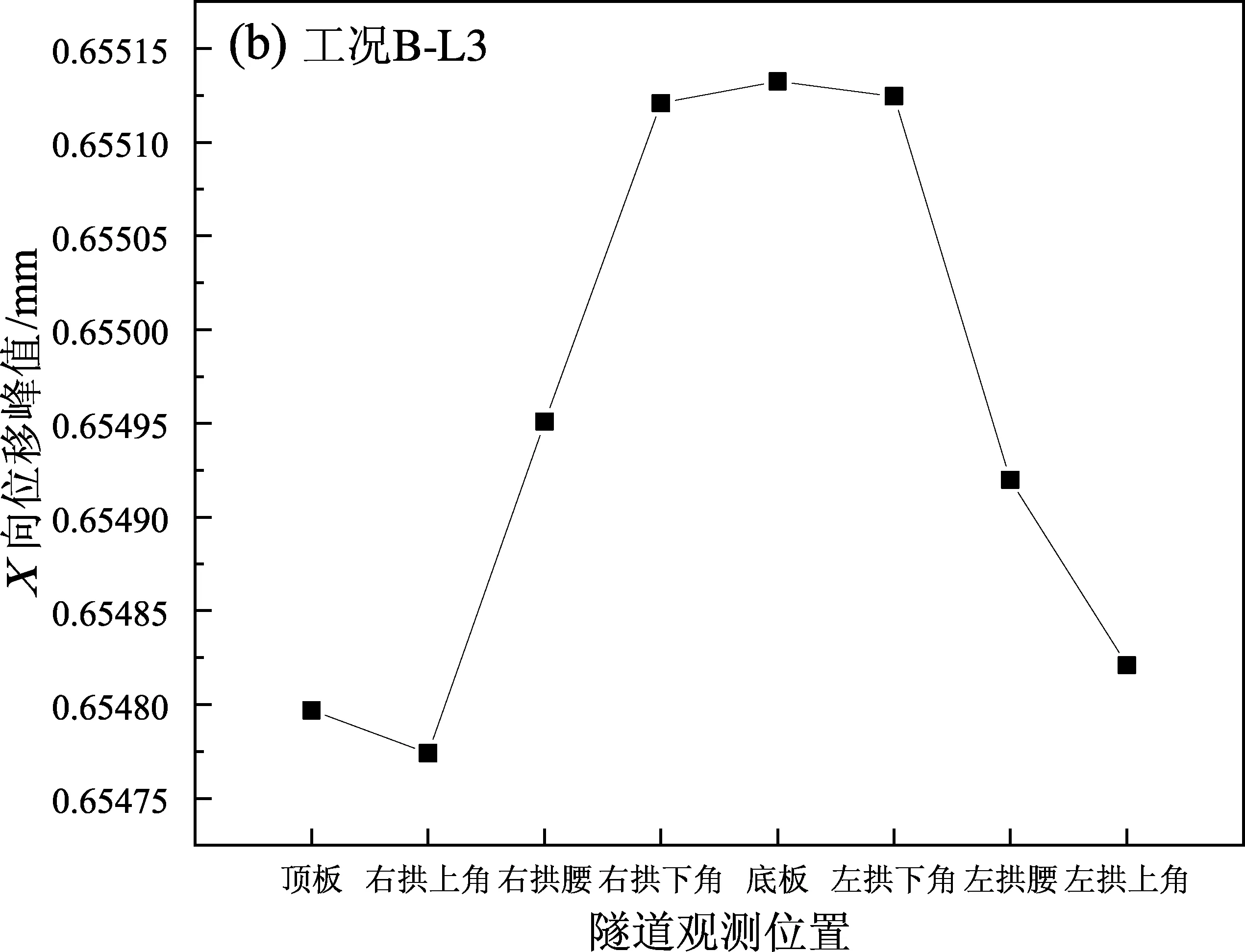
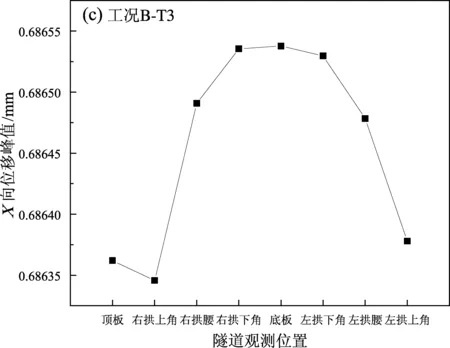
图10 各种工况下隧道各部位的X向位移峰值Fig.10 Peak displacement of each part of the tunnel in X-direction under working conditions
5 结论
通过矩形隧道结构的振动台实验与数值模拟计算,对比分析了矩形隧道结构地震动力破坏现象,重点探讨了地震作用下土-隧道结构整体力学模型的加速度时程、频谱特性、位移及土压力等方面的力学响应,得到以下结论:
(1)地震作用下矩形隧道结构的底板及拱腰处产生的位移最大,容易引起隧道结构的动力失稳。
(2)隧道结构中间部位的土压力值明显大于上、下部位,说明隧道结构中部受到的土压力最大,也最易遭受到破坏。随着台面输入地震波的峰值加速度的增大,土压力也随之逐渐增大,说明强震作用下矩形隧道承受的动土压力更大,结构的安全稳定性能就不容易得到保证,需要密切关注隧道结构的抗震承载能力。
(3)在地震作用影响下,隧道结构的4个角属于抗震薄弱位置,容易发生失稳破坏,应该采取合理的抗震加固措施来保证隧道结构的安全稳定性。
