一道新型最值问题的解法分析与变式应用

崔 鹏

(中国人民大学附属中学,100080)

圆锥曲线问题作为解析几何的核心内容,其题材丰富、解法多样.在数学核心素养中,直观感受和运算能力并重[1],这实际上是对数形结合的具体解读.在圆锥曲线相关内容的教与学的过程中,除了落实基本运算和基本方法外,还需要适当拓宽解题思路.本文通过一道以旋转变换为背景的新型最值问题的多角度分析,展示代数运算和几何观察的综合运用,并结合新课本的内容改革提供了复数解决方法[2].复数的三角形式在既定的几何条件下具有非常明显的运算优势[3],而新教材删除了极坐标系的内容,补充了复数的三角形式,本文的探讨启示我们要充分研究教材,在数学的不同模块间建立联系,抓好衔接点,就能够以不变应万变,保障数学学习活动的顺利进行.

一、问题呈现与解法分析

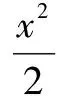
分析1旋转坐标系法

评注坐标系旋转具有很强的实用性,例如我们学习过的反比例函数和“对勾”函数,它们的图象都是双曲线,这可通过坐标旋转法得到证明.本题用坐标系旋转的方法对学生具有一定的难度,此解法只是一种参考.

分析2命题等价转化法

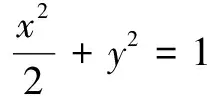
解法2(平行线法)

解法3(三角换元法)

分析3复数法

复数是高中数学的重要知识板块,在新教材[2]中还增加了复数的三角形式作为选学内容.本题可从利用复数乘法的几何意义解题的角度出发,开拓问题求解的新途径.

评注复数的三角形式是简化复数运算的重要内容,通过三角形式的运算,可以将复数的乘除法运算转化为辐角的加减运算,这本身就具备旋转的几何要求.新教材删除了极坐标表示的内容,而复数的三角形式恰好可以作为一种重要的补充,建议同学们了解掌握.

二、变式应用

复数的三角形式和极坐标有非常相似的形式,因此在类似问题上可以考虑用复数的三角形式解题.下面给出两个可以用复数三角形式简化解法的例子,供同学们思考.

变式1设A,B是椭圆x2+3y2=1上的两个动点,且OA⊥OB(O为原点),则|AB|的最大值为______.

解设点A对应的复数为z1=r1(cosθ+isinθ),由OA⊥OB,可设点B对应的复数为z2=r2(cosθ+isinθ)i=r2(-sinθ+icosθ).

依题意，由点A,B在椭圆上,可得方程组