基于问题解决 发展应用能力*

姚新国

(江苏省如皋中学，226500)

一、背景

数学应用强调数学与生活以及其他学科的联系,提升学生应用数学解决实际问题的能力.“用数学眼光观察世界,用数学思维思考世界，用数学语言表达世界”是《课程标准》提出的具体要求.高中阶段数学科的应用主要指的是数学知识与其他学科知识、生活生产实际等的外部联系,建立数学知识、数学思想方法等与理论问题或实际问题之间的联系,强调数学在所有领域的应用价值.

要真正做到懂数学、会用数学,就必须在日常学习过程中,坚持分析身边事物或者新的课程学习情境与数学的关系,针对这些关联提出问题,并能够将这些问题抽象成为可以解释的数学模型,用数学语言进行描述和表达.课堂教学可以从以下三个层面培养学生的数学应用能力:一是对现实问题的数学抽象.通过设置真实的问题情境的教学,培养学生发现问题、分析和解决实际问题的能力,促进学生真懂会用;二是用数学三种语言(文字语言、符号语言、图形语言)表达问题,培养学生信息获取和加工、数学阅读方面的能力,促进学生善于思考和规范表达的素养的发展;三是用数学知识和思想方法构建模型解决问题,培养学生逻辑推理和促进创新应用能力的提高.

二、培养数学应用能力的思维流程

案例将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm2的矩形薄钢板(如图1),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:

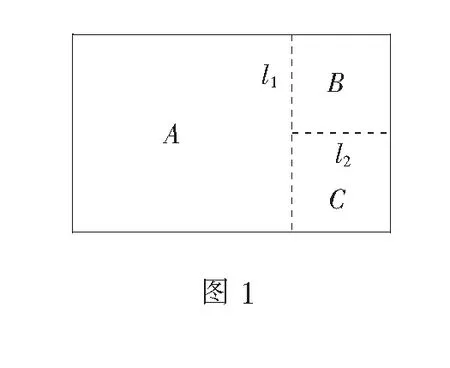
方案①:以l1为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面.

方案②:以l1为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与l1,l2垂直)作为正四棱柱的两个底面.

(1)设B,C都是正方形,且其内切圆恰为按方案① 制成的圆柱的底面,求底面半径;

(2)设l1的长为xdm,则当x为多少时,能使按方案② 制成的正四棱柱的体积最大?

本题将平面几何与立体几何的内容相结合,涉及的知识范围较广,数学模型比较复杂.对于学生来说,难点是不能依据立体图形中底面与侧面边之间的关系转化为平面图形中三个矩形的边之间的关系.

设计意图基于发展学生数学应用能力的课堂教学,要求教师在教学中明确解决问题时学生的思维障碍,揭示设计如何审题和数学探究等思维过程.

1.数学阅读,审题转化

数学阅读理解是将题目描述的数学定义、定理及其已知条件用另一种方式表达的过程,即将文字语言、符号语言和图形语言相互转化.在第(1)小问中,由矩形A裁剪为圆柱的侧面,知矩形A的长为圆柱底面的周长,进而与底面圆的半径有关;又两底面圆是正方形B,C的内切圆,故正方形B,C的边长与底面圆的半径有关.要了解A,B,C的各边之间的具体关系,可以寻找变量表示边长、半径的关系.那么如何寻找变量?一是设正方形B,C的边长,从而可以表示矩形A的边长;二是设圆柱的底面圆的半径,进一步可以表示矩形A,B,C的边长,从而建立数学模型,确定参数.在第(2)小问中,由矩形A折叠为正四棱柱的侧面,知矩形A的长是正四棱柱底面边长的四倍;又正四棱柱两底面正方形是从矩形B,C中裁剪,所以正四棱柱的表面积小于矩形铁皮的面积,且矩形B,C的边长的四倍大于矩形A的长,由此可建立不等式模型.

设计意图对于实际问题,要引导学生数学阅读,将已知条件等价转化.通过设变量表示问题中的各个量,所设变量能使其用来表示其它的量时比较方便.

2.信息整理,确立思路

信息整理是指在对大量、无序的信息进行筛选、归纳并形成解题思路的过程.提高对试题信息的处理,对条件信息的选择和处理决定了解题的方向.对图形信息的处理,数学应用能力的培养可以体现在作辅助线、对图形的分割与补体、分析图形的特征等方面,它包含信息的获取与识别、信息的处理与分析等.

面对当前的一个实际应用性问题,要设身处地进行思考,设平面图形中某些量或设立体图形中某些量作为未知量,使得选用的方法恰当、运算简洁.

设计意图从第(1)小题的求解思维过程可知,为了便于确定原矩形钢板各边之间的关系,将制作的立体几何模型还原为平面图形,有利于寻求关系,建立方程模型,直接解出半径.同时,由第(1)小问的解决过程,启迪我们研究此问题有两个角度:一是从实物平面图形求出制作模型的各量;二是从立体模型展开到平面图形,用立体模型中的量表示面积.

3.语言表达,运算推理

语言表达是指运用口头语言及书面语言,将思考过程按逻辑要求清楚表达的过程,是培养学生适应学习、生活、工作沟通交流的基本能力,是数学应用能力的体现.

第(2)小问,从原矩形钢板按比例缩小纸片模拟,裁剪为正四棱柱考虑.

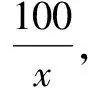
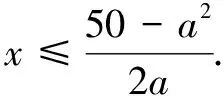
设计意图运算推理是通过理性设计运算思路而进行推理的,它不仅仅是指学生“懂了”、“会了”,更是指学生自己“悟”出道理、规律和思考方法等数学内涵.能够根据法则、公式进行运算变形;能够根据问题的条件寻找与设计合理、简捷的运算途径;能够根据要求对数据进行估计或近似计算,能够根据生活情境数学地处理相关数据问题.

4.数学应用,提升思维

数学教学是从传授知识、应用知识解决问题和在解决问题过程中提高学生的思维能力、提升学生的数学素养开始的,而我们所研究的教学内容离不开进行选择思维过程的分析,对于所遇到的数学问题需要探求问题的思路和方法,对问题的求解过程也离不开选择思维的分析与思考.同时,选择思维是与数学知识和学生的认知过程相适应的,符合数学知识内容和数学本质要求的思维过程.

设计意图选择思维只有在一定的载体下通过潜移默化的熏陶才能逐步形成.在教学中,夯实基础知识是提高选择思维的基础,在解决问题过程中灵活地选择解决问题的方法和模式,强调以提升学生选择思维为目标指向,以数学知识为载体,引导学生通过多样化的学习方式夯实基础知识,并在运用数学知识解决问题的过程中提升思维能力.

三、在课堂教学中落实培养学生的数学应用能力的反思

1.数学应用能力的培养源于学生对背景材料、实际问题的初步感觉

数学源于生产、生活实际.教学中要引导学生理解现实问题情境,简化或结构化现实模型,从现实问题情境中抽象出数学概念、数学量、数学运算等等.学生在与问题情境的有效互动中,通过对背景材料、实际问题的初步感觉,了解实际背景是什么,其蕴含了怎样的数学问题.

2.数学应用能力的培养来自在教师引导下学生对数学问题的直接感知

课堂教学中,教师要引导学生经历实际情境,通过提问、追问等方式,驱动学生去计算、推理、发现,选择方法,优化解题思路,简化计算等.学生通过对空间图形与平面图形关系的深入探究、思考,选择不同的角度、不同的代数量去解决实际问题.

3.数学应用能力的培养贵在学生对问题解决后的反思感悟

在数学课堂上,在实际应用问题获得解决后,引导学生再反思比较选择不同的变量对问题解决的影响,反思空间图形的常见转化策略等等.

培养学生的数学应用能力,要回归到现实情境中,应用数学的知识与方法分析和解决问题.教学中要运用数学的概念、定理、公式和思想方法描述现实世界的问题并解决问题,要依据问题提供的信息,进行信息整理,确定解决问题的多个方法,选择其中能够简捷地解决问题方法来表达解题过程.通过对数学问题的分析、解释、描述等形式,不断增强学生数学应用意识.