源于教材 高于教材——等和线的性质及其妙用

刘文明

(山东省临邑县第一中学，251500)

一、证明等和线定理涉及的有关结论

由教材内容,易知以下结论成立:

二、等和线定理及性质

1.等和线定理

特别地,当点P在直线AB上变化时,系数和恒为1.

2.等和线系数和的分布规律

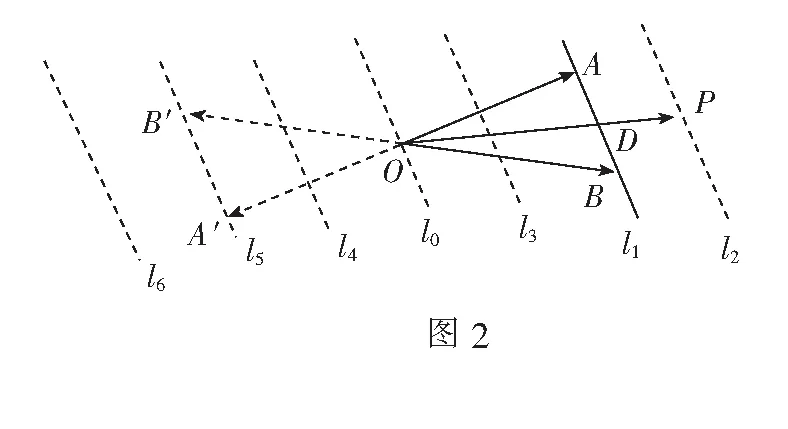
三、平面向量问题应用举例

解法1(传统解法)

解法2(等和线性质法)

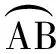
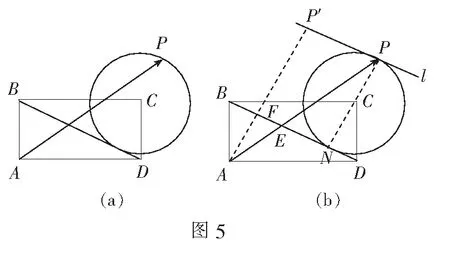
评注由以上两例可知,这类问题传统解法是先建立直角坐标系,利用向量的坐标表示和圆的参数方程求解,涉及的知识点多,计算繁琐、耗时、易错.而利用等和线性质求解,涉及的知识点单一,过程简单明了,起到了化繁为简、出奇制胜的功效.

(A)[1,4) (B)[1,4]

(C)[2,3) (D)[2,3]

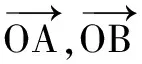
(A)(0,1) (B)(-1,0)

(C)(-∞,-1) (D)(1,+∞)

解法1(传统方法)

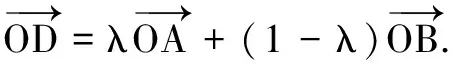
解法2(等和线性质法)

如图6(b),过点C作平行于AB的等和线l,因为OC的反向延长线交AB于圆外一点D,易知等和线l只能介于l0与l2之间,根据系数和的分布规律,得m+n∈(-1,0).

评注本题两种解法都不太难,但对做选择填空题来讲,等和线性质法更加简洁明了,节约时间.

四、从平面到空间的拓展

纵观高考、模考、培优考试题,不难发现以等和线为背景的问题常作为选择填空的压轴题出现,其综合性强、难度较大,用传统方法解决繁琐易错,而用等和线性质处理往往起到四两拔千斤的作用.同时,由于等和线定理及其性质是教材内容的适度拓展与深化,在教学过程中补充该部分知识,可启迪学生思维,体现了源于课本高于课本的教学思想,也契合高考的命题原则.