例析以立体图形为背景的概率统计问题
2022-06-22陈守俊
陈守俊
(北京市和平街第一中学,100013)
高考命题由“知识立意”转变为“能力立意”,在知识的“交汇点”设置问题已经成为命题的最大热门.综观往年各省高考试题,经常出现以立体几何图形为背景的概率统计计算问题.这些题目既考查学生立体几何、排列与组合以及概率统计的基本知识,又考查学生空间想象力及分析问题和解决问题的能力.求解这类问题的关键是思路要清晰,对基本事件的计算要不重不漏,它对学生的能力要求较高.下面试举几例说明解这类问题的思路和方法.
例1以平行六面体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率p为( )
分析本题关键在于寻找不共面的三角形的个数,当直接考虑有困难时,可从它的对立事件入手.

例2在正方体上任取3个顶点连成三角形,则所得三角形是直角非等腰三角形的概率为( )
分析本题处理的关键在于寻找直角非等腰三角形构成的特征.



解法2以A为直角顶点的直角非等腰三角形仅有Rt∆B1AD,Rt∆D1AB,Rt∆A1AC三个,故符合条件的直角非等腰三角形共有8×3=24个.
例3考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得两条直线相互平行但不重合的概率等于( )
分析本题处理的关键在于寻找两条相互平行但不重合的直线的个数.
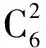
例4设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
分析本题主要考查概率统计中离散型随机变量的分布列、数学期望的求解、随机事件的有关概念与基本运算.本题属于基础题目,难度中等偏上.在求分布列时,要注意ξ的取值情况,不要遗漏.

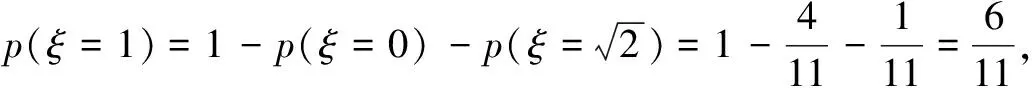

ξ012 P(ξ)411611111
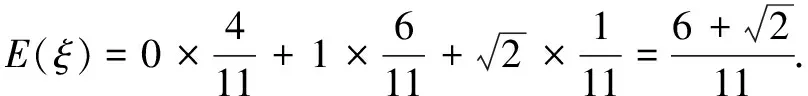
例5如图2,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).
(1)求V=0的概率;
(2)求V的分布列及数学期望.

分析此题以空间坐标为背景,给出“立体”的新定义,是以立体几何体积计算为背景的古典概型题,要求学生有较强的计算能力,熟悉古典概率的计算方法和计算公式、组合数公式、离散型随机变量分布列的意义和期望的计算等.它是在立体几何、新定义、概率等知识交汇处命制的一道新颖的综合题.
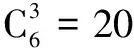


V016132343 P35120320320120
总之,我们在解决这类交汇问题时要注意审题和分析题意,寻找解题的突破口,注重总结和归纳,探求规律特征,努力提高自己的解题能力.
