五强溪水电站大坝变形预测模型研究

韩行进，杨松林，匡楚丰，陈 冰，张健飞，余天堂

(1.湖南五凌电力科技有限公司，湖南 长沙 410004；2.五凌电力有限公司，湖南 长沙 410004；3.河海大学工程力学系，江苏 南京 211100)

根据大坝原型监测资料，运用统计数学、工程力学、信息科学等建立大坝安全监控模型，定量地评估大坝的安全状况是保障大坝安全的重要手段。统计模型由于实施简单且精度能达到工程需要，因此是大坝安全监测资料分析中最常用的模型[1]。大坝安全监测常用统计模型采用的回归方法有多种[2-6]，这些回归方法各有其特点和适用性。由于大坝的情况千差万别，因此结合大坝实际特点有比较地选择分析方法，对监测资料分析的准确性、系统性具有重要影响。常用的统计分析方法有逐步回归法和偏最小二乘回归法。逐步回归法是通过计算各因子影响的显著性，去掉显著性小的因子以排除因子的共线性关系，这导致其并不一定能获得最佳回归模型[7]。偏最小二乘回归法能在自变量存在严重多重相关性的条件下进行回归建模。

近年，随着深度学习的不断发展，一些深度学习的模型，如卷积神经网络、循环神经网络等，也被应用到大坝变形预测之中[8-11]。基于深度学习的模型在解决监控模型因子不确定性和非线性问题、预测精度及泛化性等方面表现出了特有的优势。胡安玉等[12]提出一种基于长短期记忆网络(LSTM)的大坝变形预测模型，利用自回归差分移动平均模型对预测残差进行误差修正以提升预测精度。郭张军等[13]借助开源深度学习框架Tensor Flow建立了基于深度学习的混凝土坝变形预测模型。

本文研究五强溪水电站大坝变形预测的统计回归模型和LSTM循环神经网络模型。根据五强溪水电站大坝坝顶J23测点2006年至2020年的监测数据，构建含水压、温度、时效因素的逐步回归和偏最小二乘回归统计模型。取2006年～2017年的监测数据作为LSTM循环神经网络训练集数据，2018年～2020年的监测数据作为测试集数据，比较3种模型结果，获得该测点较佳的变形预测模型。

1 重力坝变形预测统计模型

1.1 数据预处理

在监测过程中，监测数据易受到环境因素影响，产生一些不符合规律性变化的监测数据，这些数据属不可靠数据。构建预测模型时应去掉不可靠数据，以提高模型预测精度。

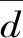
(1)

第j个监测值跳动偏差的绝对值与均方差的比值为qj，即

(2)

当qj>3时，表明该值为异常值或不可靠值。

1.2 重力坝变形监测统计模型

水压分量δH、温度分量δT和时效分量δθ是坝体位移δ的3个主要组成，即

δ=δH+δT+δθ

(3)

水压分量δH与上游水深H，H2，H3和下游水深h，h2，h3呈线性关系，即

(4)

式中，a1i和a2i均为回归系数。

五强溪水电站大坝已运行20余年，坝体内部温度达到准稳定，因此可假设坝体内部温度受气温和水温影响做简谐变化，变幅小，且有一个相位差。取年周期简谐波作为因子，温度分量δT可表示为[1]

(5)

式中，b11和b21均为回归系数；t为始测日与监测日之间间隔天数。

蓄水初期时效位移一般变化剧烈，其后渐趋平稳。根据五强溪水电站大坝实际情况，时效位移δθ可表示为

δθ=c1θ+c2lnθ

(6)

式中，θ=0.01t；c1和c2均为系数。

根据以上分析可知，五强溪水电站大坝坝体垂直位移的统计模型为

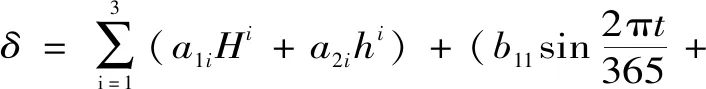
(7)

1.3 逐步回归法和偏最小二乘回归法

逐步回归法的基本思想是选取对因变量影响显著的自变量，对统计数据进行预测或建立解释模型[15]。依次将显著的自变量引入回归方程，同时从回归方程中去掉不显著的自变量。“逐步”指有的步引入自变量和有的步去掉自变量。每步均做F检验，以保证回归方程仅含显著的自变量。回归方程无显著的自变量引入就结束。

偏最小二乘回归法是多因变量对多自变量的回归[6]。设有q个因变量{x1，x2，x3，…，xq}、p个自变量{y1，y2，y3，…，yp}和n个样本点，构成了因变量与自变量的数据表X={x1，x2，x3，…，xq}和Y={y1，y2，y3，…，yp}。在X和Y中分别提取成分t1和u1(t1是x1，x2，x3，…，xq的线性组合，u1是y1，y2，y3，…，yp线性组合)。提取成分的过程中需满足：①t1和u1包含各自数据表中的变异信息越多越好；②t1和u1的相关程度达到最大。提取第1个成分后，分别执行X、Y对t1、u1的回归。若回归方程没达到满意的精度，则用X被t1解释过的残余信息和Y被u1解释过的残余信息进行第2次成分提取，直至达到满意的精度。若最终对X提取了m个成分t1，t2，t3，…，tm，执行yk对t1，t2，t3，…，tm的回归，建立yk(k=1，2，3，…，p)关于原变量X1，X2，X3，…，Xq的回归方程。

2 基于LSTM的重力坝变形预测模型

循环神经网络(RNN)利用时间序列的历史信息对时序数据建模，从而进行序列识别及预测。RNN存在梯度爆炸和梯度消失问题，因此其在长期学习方面表现十分薄弱。为了克服RNN的不足，LSTM循环神经网络使用记忆细胞代替一般循环神经网络中的隐藏层细胞，有效解决了梯度爆炸及梯度消失问题。LSTM循环神经网络中，用遗忘门、输入门和输出门等一些门控单元控制记忆细胞的输入和输出[16]。LSTM循环神经网络能有效地利用长距离的时序数据，因此非常适合进行大坝变形预测。

基于LSTM的混凝土坝变形预测模型建模步骤为[13]：①数据预处理。对监测数据进行粗差处理，去掉不可靠数据。②模型训练。将经预处理的标准化数据集训练样本作为模型输入，通过随机搜索对LSTM循环神经网络的超参数进行优化，本文激活函数采用整流线性单元函数。③模型预测。将测试集自变量因子数据输入到训练好的最优参数预测模型，获得相应的变形预测结果。④模型性能评价。

3 算例分析与讨论

3.1 工程概况

五强溪水电站工程于1999年竣工，大坝为混凝土重力坝，最大坝高85.83 m，坝顶总长719.7 m。坝顶有51个静力水准测点(见图1)，编号为J0～J47，其中在16号、44号和46号坝段各布置了2个静力水准测点，坝顶静力水准系统以右岸J0为基准，且在该部位埋设有双金属标SJ1、SJ2。基于J23测点的2006年～2020年监测数据，构建该测点垂直位移的预测模型，正值为下沉。

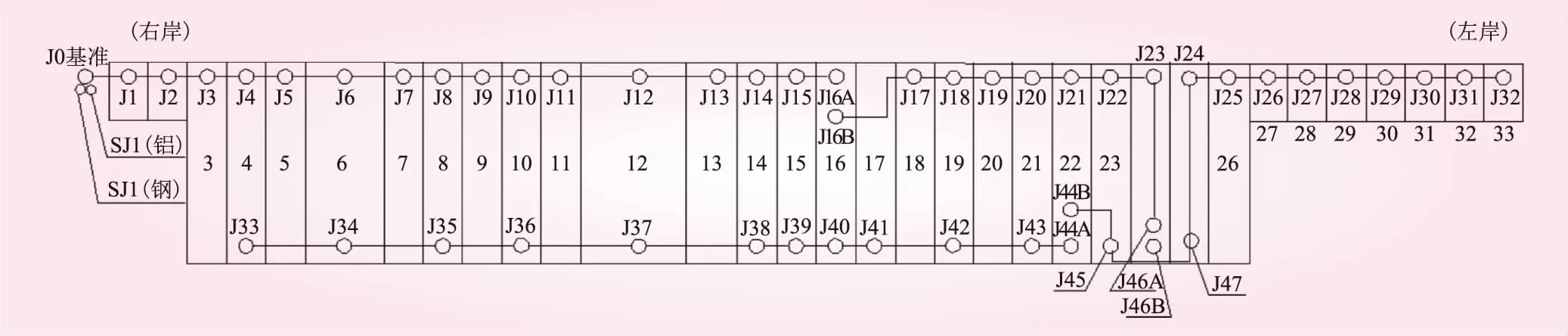
图1 坝顶静力水准布置示意

3.2 数据预处理

采用拉伊特准则确定不可靠的沉陷监测数据。图2为J23沉陷实测值过程线。去掉不可靠监测数据后，J23沉陷过程线更光滑。

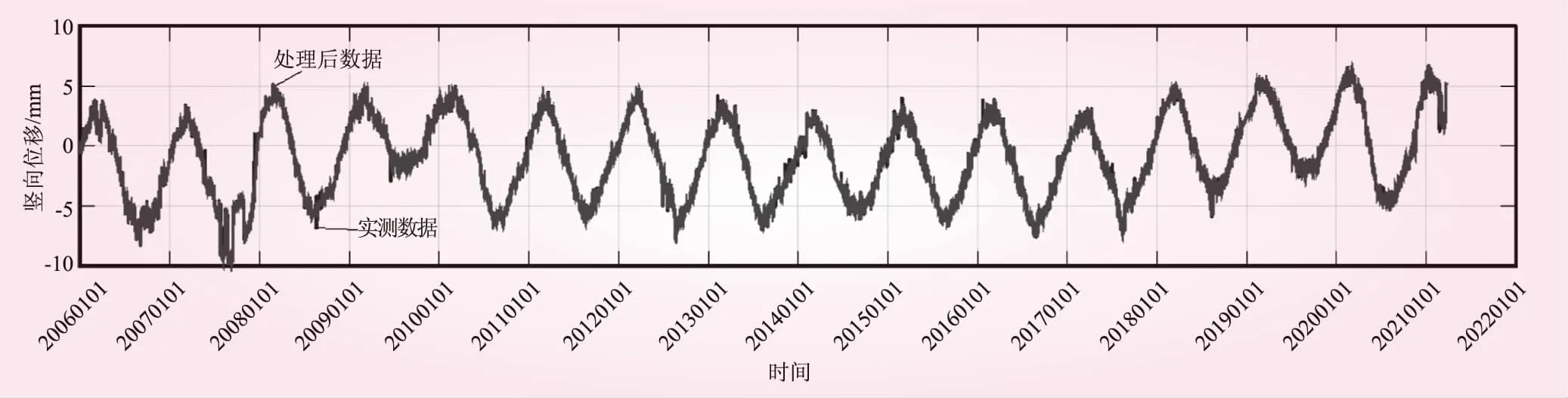
图2 J23沉陷实测值过程线

3.3 统计回归模型

为了方便表达，式(7)可以改写为

δ=a11H+a12H2+a13H3+a21h+a22h2+
a23h3+b11d+b21e+c1θ+c2f

(8)

3.3.1 偏最小二乘法回归模型

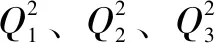
(9)

(10)

(11)

标准化位移变量的回归方程为

(12)

标准化变量还原为原始变量，可得偏最小二乘法回归方程为

y=-0.341 214-0.020 904H-0.000 156H2-
0.000 002H3+0.007 222h+0.000 047h2-
0.000 002h3-2.934 919sin(2πt/365)+
3.031 150cos(2πt/365)+0.021 690θ+
0.371 438ln(θ)

(13)

用偏最小二乘法对J23测点进行回归分析，得到的统计模型的复相关系数为0.911 8，剩余标准差为0.083 0。图3和图4分别显示了偏最小二乘法拟合曲线和各分量过程线。由图3、4可见，此模型能较好地反应坝顶沉陷的变化规律。

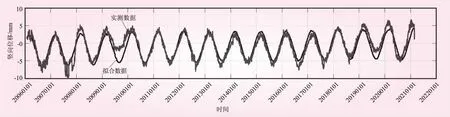
图3 J23测点沉陷变量偏最小二乘法拟合示意

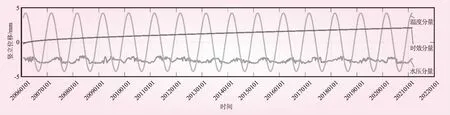
图4 J23测点沉陷变量偏最小二乘法模型各分量过程线

3.3.2 逐步回归模型

表1为逐步回归法各因子的F显著性检验，展示了各因子的显著性水平。依据因子的显著性水平，依次引入变量e、d、θ、H3、H2、f和h2，可得逐步回归方程如下：

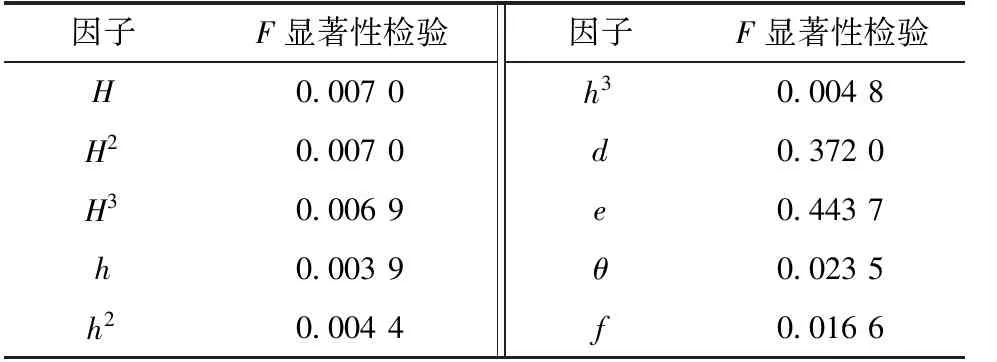
表1 逐步回归法各因子的F显著性检验

y=0.010 839H2-0.000 111 59H3+0.0016 013h2-
3.174 9sin(2πt/365)+2.831cos(2πt/365)+
0.071 16θ-1.036 9lnθ-15.219

(14)

图5和图6分别显示了逐步回归法拟合曲线和各分量过程线。用逐步回归法对该测点进行回归分析所得统计模型的复相关系数为0.916 1，剩余标准差为0.401 3。

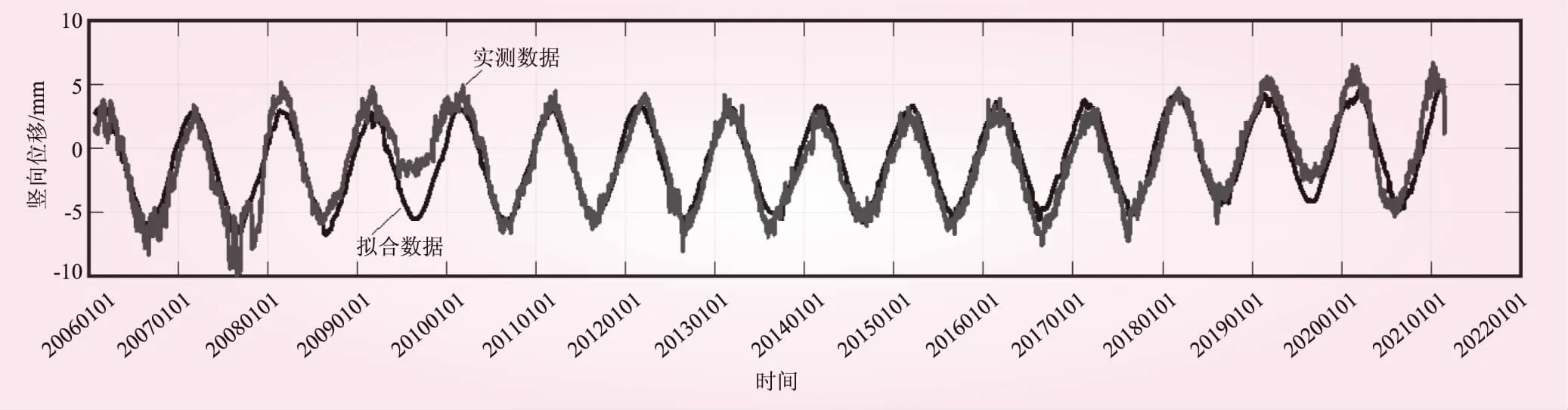
图5 J23测点沉陷变量逐步回归法拟合示意

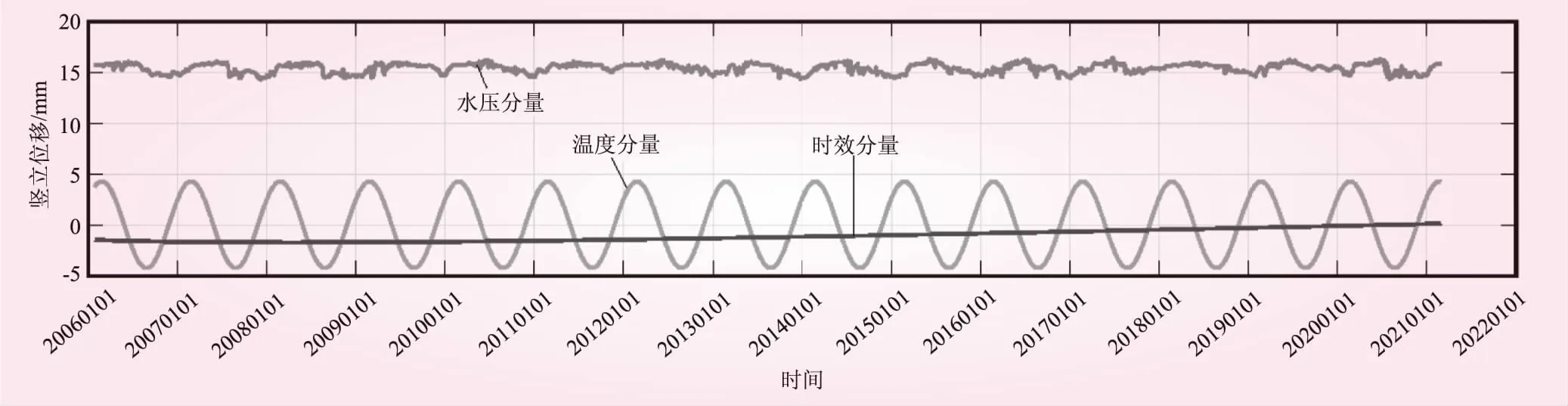
图6 J23测点沉陷变量逐步回归法模型各分量过程线

3.4 LSTM模型

根据数值试验，最终选定的LSTM模型包括2个LSTM层，激活函数采用整流线性单元函数，输入序列长度为20，即采用前20 d的沉降数据预测第21 d的沉降。训练集数据取2006年～2017年的监测值，2018年～2020年的监测数据作为测试集数据。训练后的模型在训练集上的均方根误差为0.40，测试集上的均方根误差为0.37。图7为基于LSTM模型的训练和测试过程线，预测的过程线和实测线吻合非常好。

图7 J23测点沉陷变量LSTM模型过程线

3.5 讨 论

基于逐步回归模型和偏最小二乘法回归模型的拟合效果非常相似，模型质量好，都能较好地反应坝顶J23测点沉陷变化规律。逐步回归法比偏最小二乘法的复相关系数稍高，但剩余标准差要高多了。

由逐步回归法和偏最小二乘法分量过程线可以发现，温度分量变化最为明显，水压分量和时效分量的变化较小。也就是说J23测点位移受温度变化影响较大，受水位和时效影响较小，这点从逐步回归法自变量的引入顺序也可看出，符合一般大坝运行的实际情况。温升时坝体上升，温降时坝体下沉，呈现周期性变化，这与大坝的实际情况相符。

由于水压分量中因子的线性相关性较大，逐步回归法去掉了上游水位一次项的因子和下游水位一次项与三次项的因子，一定程度上会影响回归分析精度。从这点而言，偏最小二乘回归法更有优越性。

在时效分量中，偏最小二乘回归法的拟合体现出大坝有沉降的效果，且沉降随时间的推移会逐步变缓；逐步回归法的拟合体现出大坝有上升的效果，上升量随时间的推移会减小。测点不是以大坝建成的时间作为统计模型的起始时间，因此时效分量一开始就有位移。一般而言，正常运行的大坝时效位移变化规律为初期变化急剧，后期渐趋于稳定，但由J23测点的真实位移曲线可以看出，该测点有明显的沉降趋势，因此两种模型的时效分量都未趋于稳定值，符合实际情况。整体上看偏最小二乘法获得的时效分量更符合真实情况。

图8比较了3种模型的预测过程线。LSTM模型的精度最高。由于统计模型是基于15 a的监测数据进行回归拟合的，跨度较大，因此其精度有所降低。用12 a的监测数据进行训练，预测3 a的数据，由此可见，在训练数据充足的情况下，LSTM模型的预测精度高，符合深度学习算法的特点。

图8 J23测点沉陷变量预测过程线比较

综上，3种模型均能有效地预测J23测点位移，采用偏最小二乘法回归模型或LSTM模型更为妥当。

4 结 论

采用基于逐步回归法、偏最小二乘回归法和长短期记忆(LSTM)循环神经网络构建了五强溪水电站大坝坝顶J23测点沉陷的预测模型，对比分析预测效果和各分量对位移值的影响，得出以下结论：

(1)从复相关系数上来看，偏最小二乘法与逐步回归法拟合效果相似，偏最小二乘法获得的剩余标准差更低。

(2)逐步回归法去掉了一些因子，使得分量在还原时效果不太理想，具有较大的残差值。偏最小二乘法考虑因子全面，解释各分量更严谨。

(3)训练数据充足的情况下，LSTM循环神经网络能高精度地预测变形。

(4)J23测点沉陷采用偏最小二乘法回归模型或LSTM模型进行预测更为妥当。