风电机组叶尖净空分析与控制
2022-06-22王文亮张国强李璇烨
王文亮,张国强,李璇烨
(1.国电联合动力技术有限公司,北京 100039;2.风电设备及控制国家重点实验室,北京 100039)
0 引 言
随着技术的发展成熟以及对制造成本的要求,风电机组单机容量不断增大,风轮直径越来越长。目前陆上风电机组单支叶片长度已经达到80 m,海上机组甚至超过了100 m。叶片逐步大型化势必会带来重量的增加和载荷的变大,考虑制造成本等多方面因素,目前常用的解决方法是将叶片设计越来越柔软。
叶尖净空是指风电机组叶片在运行过程中叶尖到塔筒表面的几何距离,在叶片经过塔筒附近时此距离达到最小,最小净空距离是目前风电机组设计过程中的考虑的主要极限之一[1]。叶片柔性的增加势必带来变形的增加,给叶尖净空带来不利影响。在机组运行过程中,若叶尖净空值太小,极可能发生叶片扫塔现象,造成叶片结构损坏,严重时可能引起倒塔事故,造成重大人身财产安全。文献[2]采用独立变桨的方式,提高叶尖净空的同时,降低了关键零部件的疲劳载荷。文献[3]通过在未达到额定风速时提前变桨的控制方法,减小了机组推力,增大了最小净空距离,算法简单但对发电量有一定的影响。文献[4]通过净空传感器装置,监测可能发生扫塔的叶尖净空,采用模糊逻辑控制器实现了最小净空的控制。
本文基于风轮的空气动力学特性,分析了影响叶尖净空的因素,提出了一种基于净空距离监测反馈的控制算法,并对仿真结果进行了分析。仿真结果表明净空监测及控制算法系统的有效性,具有推广应用价值。
1 风轮气动性能分析
1.1 风轮气动特性分析
风电机组由多种设备组成,运行时具有多个运动自由度,机组设计需对此进行结构动力学特性分析,主要分为有限元法和模态分析法2种。DNV公司的Bladed软件是风电机组设计和载荷计算常用软件之一,其采用模态分析理论,将叶片、塔筒等部件作为柔性部件进行建模,能够对静态曲线和动态运行进行仿真。
叶片是典型的柔性部件,分析时可将叶片假设为沿叶展方向的多个刚性节点的组合。不考虑塔筒变形时,叶尖净空距离是叶片各节点位移的累计,在垂直于风轮平面方向的投影。对于叶片任意节点,运动方程为[5]
(1)
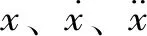
叶尖变形可简化为仅考虑垂直风轮平面方向的位移,此时合外力Fa主要是叶片节点的空气动力学推力。
根据动量叶素理论[5-6],风轮所受推力可以表示为
(2)
式中,ρ为空气密度;R为风轮半径;V为来流风速;CT为推力系数。
推力系数是风轮自身的气动特性之一,主要由叶尖速λ比和桨距角β决定[7]。叶尖速比λ是无量纲变量,表示风轮叶尖的线速度与风速的比值,将风速V和风轮转速w两个变量综合为一个变量进行分析
λ=(w×R)/V
(3)
据此,在特定风速下,风轮所受推力正比于风轮推力系数,式(2)可以化简为
FT=KfCT(λ,β)
(4)
1.2 静态曲线
以2 MW某机型为例,基于Bladed软件在切入风速到切出风速区间内进行静态曲线计算,如图1所示。
图1a为风轮推力随风速变化的静态曲线,可以看出,低风速段随着风速的增加,风轮推力逐渐变大;在额定风速附近,机组受到的推力达到最大;额定风速以上随着风速的增加,推力值反而变小。
静态曲线仿真结果可以得到运行风速区间内桨距角(见图1b)和叶尖速比(见图1c)随风速的变化情况。

图1 目标风电机组的静态曲线
图2为阶梯仿真风速及对应叶尖净空示意。由图2可以看出,叶尖最小净空随着风速的增加先变小后变大,在额定风速附近达到最小。结合图1a的静态推力曲线,叶尖最小净空与风轮推力呈现明显负相关非线性关系,因此可将叶尖最小净空LC0表示为
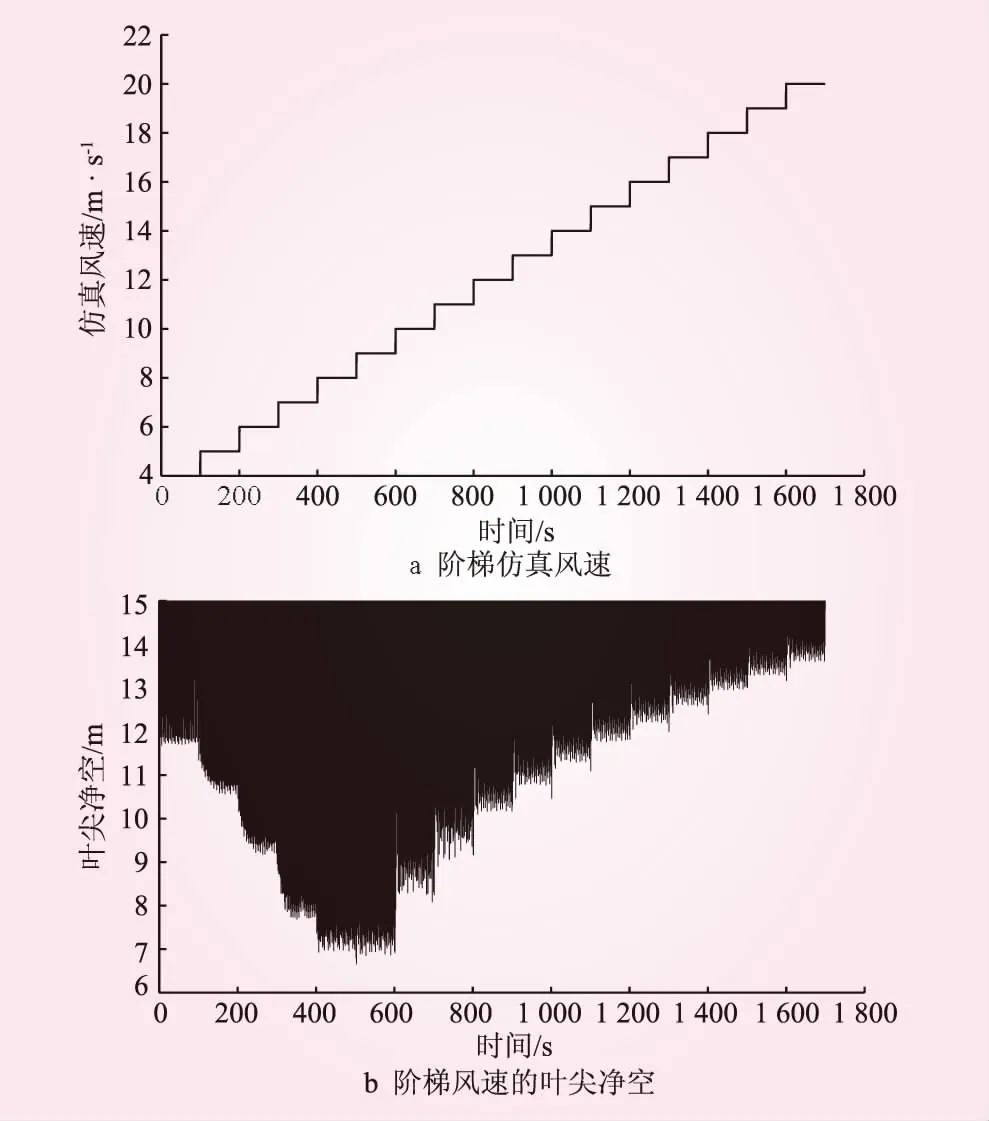
图2 阶梯仿真风速及对应叶尖净空示意
Lc0=G(FT)
(5)
式中,G表示负相关。
将式(4)带入式(5),得到
Lc0=G(KfCT(λ,β))=KcGc(CT)
(6)
2 叶尖净空影响因素分析
由上节可知,叶尖净空最小值出现在风轮所受最大推力时刻,而推力值与推力系数成正比,因此,增大叶尖净空值的目标就可以转化为减小特定风速下推力系数CT。由图2可知最小净空出现在额定风速附近,因此,将运行区间分为低风速(6 m/s)和高风速(14 m/s)2种情况分别进行具体分析。
推力特性可用推力系数CT随叶尖速比和桨距角变化的一簇曲线表示[8],图3、4为不同桨距角的CT曲线。

图3 小风下的推力系数曲线
2.1 低风速(6 m/s)
由图1风电机组的静态曲线可知,6 m/s风速对应的桨距角β=0,叶尖速比λ=11.62,对应于图3曲线的A点。
根据图3曲线趋势,减小A点对应的CT可从2方面分析:减小叶尖速比λ,使A点CT沿β=0 rad曲线向B点移动。风速一定时可降低当前风轮转速实现;增大桨距角β,使CT-λ曲线下移,即A点CT沿AC方向移动。增大桨距角可通过变桨控制实现。
2.2 高风速(14 m/s)
由图1静态曲线可知,14 m/s风速对应的桨距角β=0.22 rad,叶尖速比λ=5.98,对应于图4曲线的A点。

图4 大风下的推力系数曲线
与低风速情况类似,也可以从2个方面来降低A点对应的CT:增大叶尖速比λ,由于大风时机组运行转速已达到额定限值,无法增大风轮转速,此方法无法实现;增大桨距角β,大风时变桨控制系统在实时动作,此时可通过叠加一个额外桨距角来实现净空控制。
3 策略控制算法实现
综合上节净空分析结果,本文设计了一种基于机组运行状态的净空监测与控制系统。实时监测机组运行过程中叶片净空的变化情况,通过主控系统预防净空距离劣化,并在检测到危险净空时启用机组保护机制。
3.1 净空监测系统
本净空控制算法基于一套高精度净空监测系统,在机舱位置处安装高速摄像机,实时拍摄叶片穿越塔筒位置处图像,经过智能图像识别技术,将图像数据转为实时的叶尖净空距离Lc,传输到主控制系统。
3.2 算法实现架构
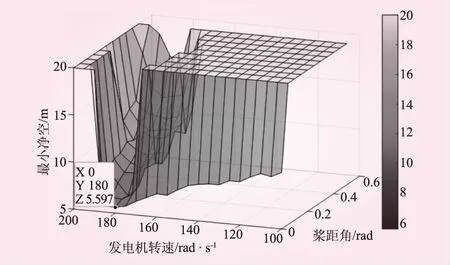
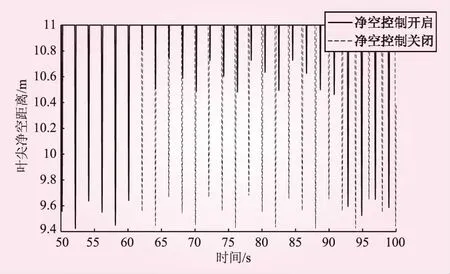
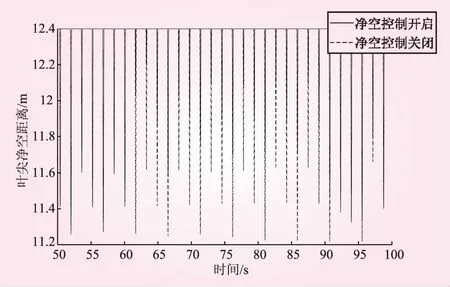
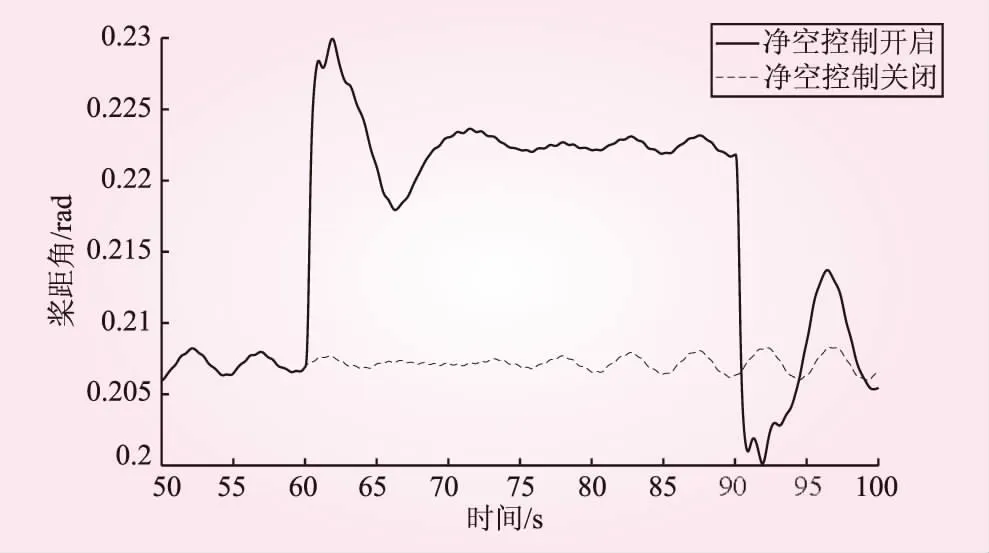
本净空控制系统采用实时动态阈值方式,覆盖整个机组运行范围,保证机组在全风速下不发生叶尖扫塔事故。控制算法根据当前的运行状态数据,计算出实时的净空控制阈值Lt和净空危险阈值Ltmin。净空控制阈值Lt表示启用净空控制的下限值,净空危险阈值Ltmin表示启用安全保护条件的下限值,Ltmin 通过对比实测净空值Lc和两阈值的关系,进入相应的控制流程,整体算法架构如图5所示。 图5 净空控制算法流程 实测净空值Lc>Lt时,代表当前运行净空处于正常范围,不需要启用净空控制。若Lc 由上节可知,机组运行状态可依照风速划分多个区间,每个区间设置不同的Lt和Ltmin。通过对大量运行数据的统计分析,得到每个风速区间的最小净空距离统计表1D-Lt(V),如图6所示。 图6 不同风速段的最小净空距离 目前风电机组风速数据来源于风轮后的风速仪,测量值受到风轮、叶片等扰流等影响,可靠性不高。实际控制系统中机舱风速测量值一般不作为控制输入量,本文设计了基于发电机转速Wg和桨距角β的二维净空阈值表:2D-Lt(Wg,β)。机组运行状态根据不同的发电机转速和桨距角组合,形成多个运行区域。图7为数据统计的叶尖最小净空在不同发电机转速和桨距角区域内的大小。 图7 最小叶尖净空2D阈值曲面 考虑机组的净空安全裕量和设计极限,统计图中最小净空值乘以相应的设计系数,即可得到净空控制阈值表和净空危险阈值表。根据机组的运行状态和外部环境等数据,可将机组运行状态进一步细化,形成多维的净空阈值表。此部分内容暂不在本文中展开讨论。 由于无法通过软件仿真的方式实时改变叶尖变形程度,本文采用程序模拟净空超阈值的方式,在60~90 s时间段内触发超限故障,分别在6 m/s和14 m/s工况下,仿真了无净空控制和启用净空控制的开环控制效果。 图8为在6 m/s风速下开启和关闭控制算法叶尖净空对比。从图8可以看出,开启净空控制算法与关闭净空控制算法相比,最小叶尖净空值从9.4 m增大到10.5 m,增大了11.7%;并且控制响应时间很快,在超限触发后,下一支叶片净空值实现了显著的增加。图9为2种仿真的桨距角对比,可以看出,开启净空控制算法,在6 m/s风速进行了一定角度收桨。 图8 开启和关闭控制算法叶尖净空对比 图9 小风速净空控制开启与关闭桨距角对比 图10为14 m/s风速下开启和关闭控制算法叶尖净空对比。从图10可以看出,开启净空控制算法后最小叶尖净空值从11.2 m增大到11.6 m,增大了3.57%,此时净空值超阈值程度小,故调节动作量较小;控制响应时间很快,在超限触发后下一支叶片净空值就实现了显著的增加。图11是2种仿真的桨距角对比图,在转速控制桨距角变化的基础上,叠加了净空控制的桨距角需求。 图10 开启和关闭控制算法叶尖净空对比 图11 大风速净空控制开启与关闭的桨距角对比 本文以柔叶片风电机组为研究对象,采用空气动力学性能分析了叶尖速比和桨距角对推力系数的影响,提出了针对叶尖净空的有效控制方式;基于叶尖净空探测设备设计了一套净空监测与控制系统;根据仿真数据整合得到净空控制阈值和净空危险阈值。以某2 MW模型仿真了净空控制算法的叶尖净空距离控制效果,可得出以下结论: (1)叶尖净空距离随风速变化先减小后增大,最小净空出现在额定风速附近。 (2)叶尖净空与风轮所受推力呈负相关关系,即改变风轮推力可以实现叶尖净空距离的调整。 (3)仿真结果表明净空控制算法实现了叶尖最小净空距离的调节,并且能够快速响应。 (4)净空监测与控制系统的应用,能够有效避免叶片扫塔事故发生,具有重要的应用推广价值。
3.3 净空阈值确定

4 控制仿真结果
4.1 低风速(6 m/s)仿真结果
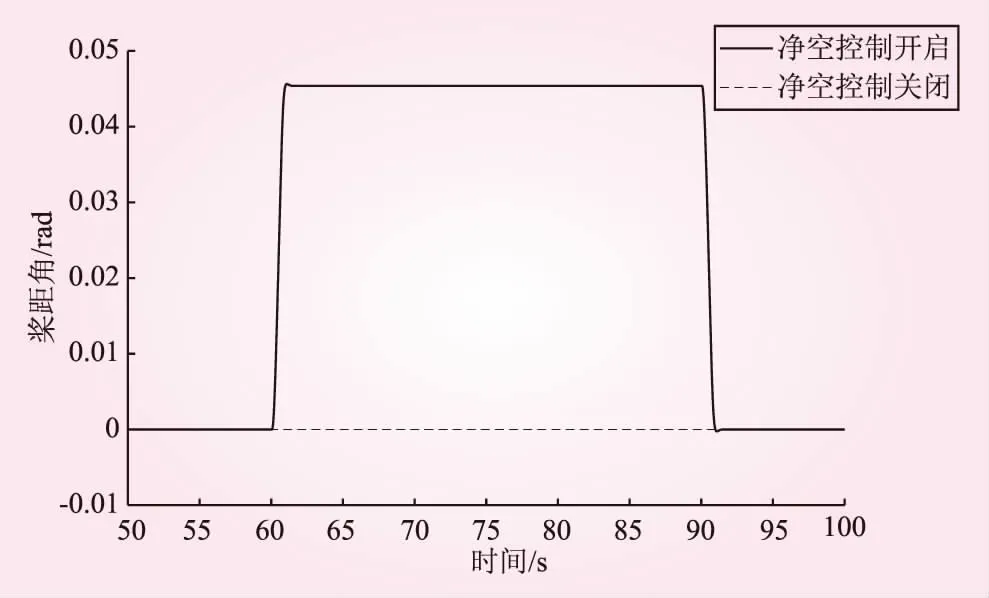
4.2 高风速(14 m/s)仿真结果
5 结 论
