基于卡尔曼预测粒子滤波的复杂场景图像目标跟踪算法

张 博

（长沙师范学院 信息科学与工程学院，长沙 410100）

随着计算机技术的兴起与发展，计算机能够对视觉信息进行相应的处理与应用，极大推动了计算机视觉的兴起与发展， 受到了多个领域的关注，相对应的研究也逐渐增多。 在计算机视觉领域中，关键部分就是对动态图像进行处理与分析，以此来获取有效的、有用的信息。 动态图像会随着时间变化产生相应的变化， 并能够表示为空间位置函数，存在着丰富的信息， 其处理过程涉及多种领域知识，例如图像分析领域、计算机视觉领域、人工智能领域等。 动态图像分析是现今计算机领域中发展较为活跃的分支，对其进行深入探究具有现实意义。

就现有研究成果来看，主流目标跟踪算法主要包含7 类，分别为基于对比度的目标跟踪算法（一种基于改进混合高斯模型的运动目标检测算法[1]），该算法主要利用背景与目标之间的对比度对目标进行识别与跟踪，优势为对目标姿势变化适应性较强，劣势为目标识别能力较差，无法应用在背景复杂目标跟踪中；基于区域匹配相关的目标跟踪算法（基于边缘匹配的平面目标跟踪[2]），该算法以图像目标全局信息为基础，例如颜色、纹理等对目标进行识别与跟踪，优势为目标识别精度较高，劣势为运算量大；基于特征点的目标跟踪算法（基于特征点的KLT 实时目标跟踪算法实现[3]），该算法选取多个奇异点，作为图像目标特征点，对其进行提取、保存等操作，对目标进行实时跟踪。 优势为目标跟踪精度较高，劣势为目标跟踪时效性较差；基于变形模板的目标跟踪算法（复杂背景下基于自适应模板更新的目标跟踪算法研究[4]），该算法以目标模板为基础， 通过模板纹理方向变形检索图像中的目标，优势为适应较为复杂的背景，劣势为耗费时间较长；基于光流的目标跟踪算法（基于运动预测的优化光流目标跟踪算法[5]），该算法以目标光流场为依据，通过聚类速度相近的光流场区域，即可完成目标的提取与跟踪，优势为运算量较小，适合跟踪速度较大的目标，劣势为算法对噪声较为敏感；基于机器学习的目标跟踪算法（基于机器学习的单线激光雷达进行车辆识别与跟踪方法研究[6]），算法应用机器学习理论将目标跟踪问题转化为目标分类问题，即分类图像中的目标与背景，确定目标的位置，优势为计算量较小，目标跟踪可信度较大，劣势为算法较容易陷入局部最优；基于贝叶斯滤波的目标跟踪算法（用于目标跟踪的智能群体优化滤波算法[7]），该算法应用先验信息对目标的当前状态进行估计，实现目标跟踪，优势为目标跟踪精度较大，劣势为随着先验信息的增加，算法速度逐渐减缓，无法跟踪速度较快的目标。

在现有研究成果的基础上，本文提出基于卡尔曼预测粒子滤波的复杂场景图像目标跟踪算法研究。

1 复杂场景图像目标跟踪算法研究

1.1 复杂场景图像背景提取

此研究采用ViBe 算法对复杂场景图像中背景进行提取与建模，为后续目标状态转移模型的构建提供便利与支撑。

复杂场景图像背景提取步骤如下所示：

步骤一：假设复杂场景图像背景模型表达式为

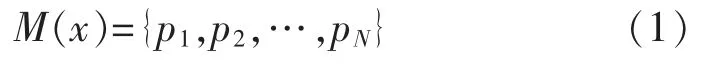
式中：M（x）表示背景模型；pN表示背景像素点，总数量为N。

依据式（1）对背景模型进行初始化，以此为基础，从第二帧开始对图像背景进行相应的检测。

步骤二：对图像中的背景与前景进行判断。 比较背景模型M（x）与图像像素p（x），并对相似度进行计算，计算公式为

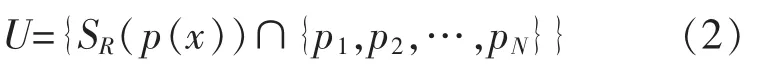
式中：U 表示待分类像素与背景模型的相似度；SR（p（x））表示以图像某像素点为中心，以R 为半径的球体。

则图像背景与前景的判断规则为

式中：Umin表示给定阈值，以此为基础来判定图像的背景与前景。

步骤三：在背景模型M（x）中，随机选取一个样本，对像素值进行替代，完成背景模型的实时更新与提取。

1.2 图像目标状态转移模型构建

为了提升图像目标跟踪的精确性，构建模型需要与实际目标运动符合[8]。 现今应用较为广泛的状态转移模型为仿射模型与自回归模型[9]。 其中，仿射模型表达式为

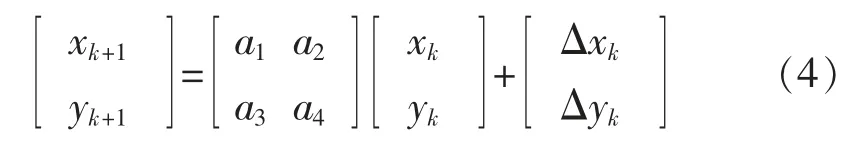
自回归模型表达式为

式中：ax，ay，bx，by表示线性参数；ux与uy表示高斯噪声，并且两者相互独立。

1.3 图像目标观测模型构建

为了满足图像目标的跟踪需求，此研究以目标颜色直方图为基础，构建图像目标观测模型[10]。在目标跟踪的初始帧，需要对目标进行手动选择，设定初始时刻目标为T0，对应的颜色直方图为H0。 在目标跟踪过程中，设定候选目标为T，对应的颜色直方图为H。 目标观测模型就是通过比较H0与H 之间的相似度，来实现目标的观测与粒子权重的计算。

依据复杂场景图像目标跟踪需求，选取Bhattacharyya 距离方法对直方图之间相似度进行计算。Bhattacharyya 距离计算公式为

式（6）计算得到的dBhattacharyya（H0，H）数值越大，表明直方图之间的相似程度越低，dBhattacharyya（H0，H）数值越小，表明直方图之间的相似程度越高。

粒子权重数值计算公式为

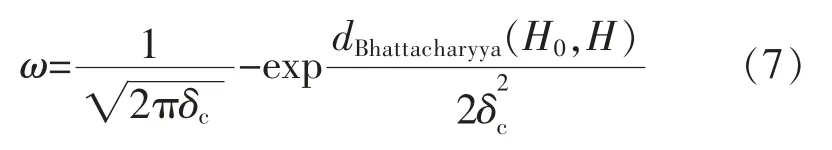
式中：ω 表示粒子权重数值；δc表示选取的固定常数，取值范围为0～1。

通过式（7）可知，随着dBhattacharyya（H0，H）数值的增大，粒子权重数值呈现逐渐下降趋势，即直方图的相似程度越低，粒子权重数值越大。

1.4 图像目标状态估计

基于卡尔曼预测粒子滤波估计图像目标状态过程实质上就是目标状态预测及其修正过程，具体如下所示：

假设图像目标状态数学描述为

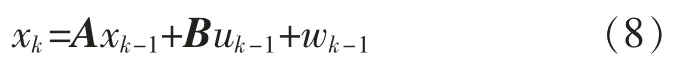
式中：xk表示当前帧的图像目标状态；A 与B 分别表示状态转移矩阵与状态控制矩阵；xk-1表示前一帧的图像目标状态；uk-1表示前一帧的高斯噪声；wk-1表示前一帧的随机状态噪声。

通过构建目标观测模型即可获得图像目标观测量，表达式为

式中：zk表示图像目标观测量；G 表示状态观测矩阵；vk表示观测噪声。

为了方便研究的进行，设定随机状态噪声与观测噪声相互独立，两者均符合正态分布，即可将其转换为

式中：Q 与P 分别表示随机状态噪声与观测噪声对应的协方差。 常规情况下，Q 与P 是随着时间产生变化的，但是为了研究的便利，认定两者均为常量。

当迭代次数为k 时，图像目标状态估计误差表示为

式中：ek表示目标状态估计误差；表示目标状态估计误差修正值。

则均方误差表达式为

当均方误差达到最小值时，即可获得图像目标状态预测方程组，定义为

相应的图像目标状态修正方程组表达式为

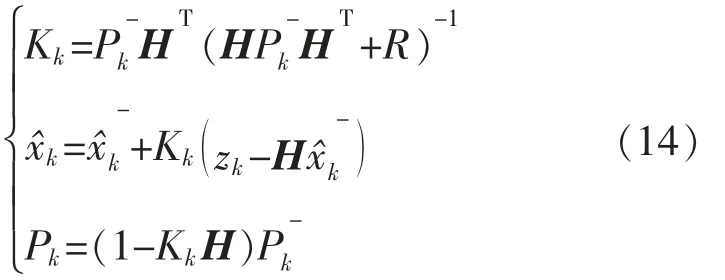
式中：Kk表示修正控制系数；Pk表示修正后的估计误差；表示修正后的估计值。

通过上述过程完成了图像目标状态的精确估计，确定了每帧图像目标的运动状态，为后续图像目标跟踪的实现提供依据。

1.5 图像目标跟踪实现

在目标跟踪过程中，能够依据粒子权值估计粒子的状态，估计公式为

式中：X 表示粒子状态的估计结果；ωi表示粒子权重数值。

依据粒子滤波的原理，推出复杂场景图像目标跟踪算法，具体步骤如下所示：

步骤一：初始化。 手动选取目标模板，并计算对应直方图。 与此同时，依据先验分布构建初始状态样本集，表达式为

步骤三：计算粒子权重数值，并对其进行归一化处理，即：

步骤四：图像目标状态估计，将估计结果记为xk。

步骤五：累计求和处理粒子集权重，利用均匀分布的随机数来对粒子集进行重新采样，生成新的粒子集。

步骤六：重复进行步骤二到步骤五，直到锁定图像目标的具体位置为止。

综上所述，此研究应用卡尔曼预测粒子滤波实现了复杂场景图像目标的跟踪，为图像信息应用提供充足的帮助。

2 实验与结果分析

为了验证提出算法的应用性能，应用引言所述7种主流算法（编号1～7）与提出算法进行实验，通过对比分析显示提出算法的应用性能，具体如下文所述。

2.1 图像目标跟踪定量分析

为了验证提出算法是否能够改善现有主流算法存在的问题，构建图像目标仿真模型，表达式为

为了方便实验的进行， 设定uk与vk均值为0，方差为10 与1。 同时，设置卡尔曼预测粒子滤波方法中粒子数量为100，阈值取值为30，迭代次数为100 次。

定量分析即选取一个评价指标对图像目标跟踪效果进行数值评价。 实验以图像目标跟踪误差的方差作为评价指标，其计算公式为

以式（20）为依据，通过实验计算每个算法应用后的RMSE 数值，具体数据如表1 所示。

表1 RMSE 数据表Tab.1 RMSE data sheet

常规情况下，RMSE 数值越小，表明图像目标跟踪误差越小，则算法的应用性能越好。 如表1 数据所示， 与7 种主流算法相比较， 提出算法的RMSE数值最小，表明提出算法的目标跟踪误差最小。

2.2 图像目标跟踪定性分析

实验选取某段视频为依据，将视频中运动车辆作为实验对象，采用7 种主流算法与本文算法对其进行跟踪，获得结果如图1 所示。

图1 图像目标跟踪结果示意图Fig.1 Schematic diagram of image target tracking results

如图1 所示，主流算法与提出算法均能够跟踪到图像目标，但是7 种主流算法搜索窗口变化性较大，跟踪窗口内包含着较多背景图像，这非常容易造成后续目标跟踪的失败。 而本文算法目标跟踪窗口较为规范，并且窗口内包含背景信息较少，更有利于后续目标的跟踪。

2.3 复杂背景目标跟踪结果分析

为了增加实验结论的准确性，在不同背景复杂度下进行实验， 验证算法在不同场景下的适用性。以背景复杂度为自变量进行实验，获得图像目标跟踪结果如图2 所示。

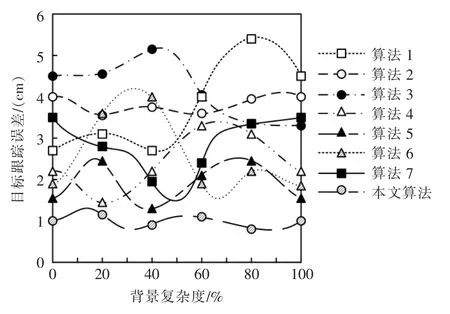
图2 不同背景复杂度下目标跟踪结果示意图Fig.2 Schematic diagram of target tracking results under different background complexity

如图2 所示，相较于7 种主流算法来看，本文算法目标跟踪误差较小，主要是因为本文算法在目标跟踪前对图像背景进行了相应的提取，可以有效降低背景在目标跟踪过程中的影响，从而降低了目标跟踪误差。

2.4 图像目标跟踪时间分析

图像目标跟踪时间也是显示算法应用效果的重要指标之一。 常规情况下，图像目标跟踪时间越短，表明算法应用效果更佳。 通过实验获得图像目标跟踪时间如表2 所示。

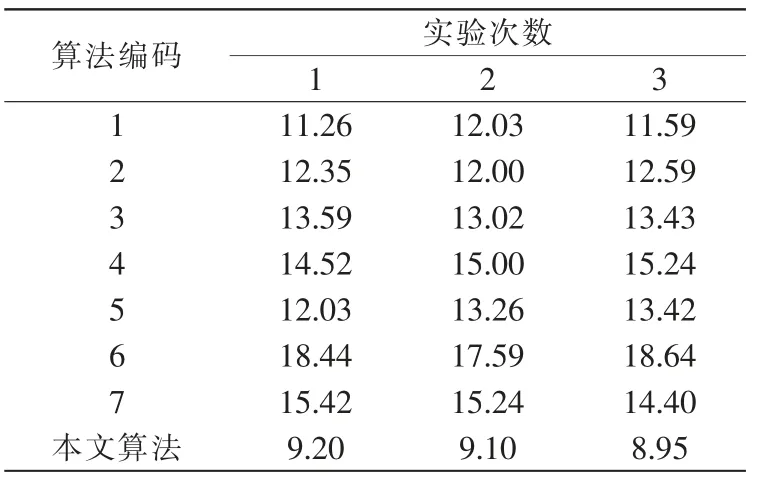
表2 图像目标跟踪时间数据表Tab.2 Image target tracking time data t/（ms）

如表2 数据所示，与7 种主流算法相比较，本文算法图像目标跟踪时间较短，能够更及时地获得目标跟踪结果。

3 结语

此研究利用卡尔曼预测粒子滤波推出了新的复杂场景图像目标跟踪算法，通过实验得到其平均RMSE 值为9.08，平均跟踪时间为10.30 ms，充分证实了提出算法具备较好的应用效果，能够满足复杂场景图像目标跟踪需求，为计算机视觉发展提供助力。