超冷原子中拓扑超流的发展现状

冯 鉴，张伟伟，林良伟，蔡启鹏，张义财，刘超飞*

1. 江西理工大学理学院，赣州341000

2. 广州大学物理与电子工程学院，广州 510006

目 录

I. 引言

Majorana费米子是意大利物理学家Ettore ·Majorana在1937 年预言的[1]， Majorana 费米子源自于狄拉克费米子[2]，通过给狄拉克旋量施加一个现实条件而得到[3]。与狄拉克费米子不同的是， Majorana 费米子的产生算符γ†和湮灭算符γ 相等, 即其反粒子等于自身, 粒子呈电中性。非阿贝尔拓扑序在容错量子计算中具有潜在应用，所以近年来该系统引起了人们的广泛关注。研究表明，支持非阿贝尔激发的拓扑非平庸超流体相既可以从s 波超流体中诱导出来，也可以从具有本征手性p 波配对的系统，例如分数量子霍尔系统、手性p 波超导体和超冷费米子中的p 波超流体诱导出来。利用对称性，可以将拓扑超流体分为时间反演不变的拓扑超流体和时间反演对称破缺的拓扑超流体。具有时间反演不变的拓扑超流体在块体系统里面存在超流配对能隙，其表面态具有Majorana 费米子。Kitaev首先指出，具有p 波相互作用的一维无自旋费米子系统具有拓扑上非平庸的超流体相，在边界处存在零能量Majorana 费米子。

受制于化合物的天然性质[4]，人们在寻找固态结构中的拓扑材料时必须依靠偶然性[5–7]。然而，超冷原子系统提供了一个更方便的研究平台。人们可以在超冷原子系统中创建各种光学晶格，在其中调整跃迁和原子间的相互作用[8]，甚至可以添加杂质到光晶格中[9]。光晶格中的超冷原子为研究量子多体问题提供了一个良好的平台。基于现有的光学技术，超冷原子气体的高度可控性和有序性，使其成为发现非平庸拓扑相的理想平台，这些拓扑相在普通凝聚态系统中难以实现或被证明[10–12]。因此，超冷原子系统灵活的可调性，为设计晶格哈密顿量和实现新型拓扑相提供了更多的机会[13–15]。此外，理论上提出的模拟规范场在实验中被成功实现，使得冷原子系统的拓扑量子态成为当前的研究热点[16–18]。

另一方面，人们在常规s 波相互作用费米气体中合成有效p 波相互作用方面取得了重大进展。沿着这条线的第一个进展是在原子系统中实现了人工自旋轨道耦合，这是Kitaev 模型的推广[19]。在一个s 波费米气体中，Rashba 自旋轨道耦合可以诱导自旋三重态配对，从而在二维系统中产生手性p 波超流体[20,21]。自旋轨道耦合是电子在凝聚态系统中普遍存在的现象，被认为是拓扑绝缘体[22]、量子自旋霍尔效应等许多有趣现象的关键组成部分[23]。超冷原子系统中人工规范场的实现，使人们能够利用超冷原子的特点，如清洁的环境和高度可控的参数，为研究这些现象开辟了新的途径。自旋轨道耦合的引入可能有助于解释从巴丁–库珀–施里弗理论(Bardeen-Cooper-Schriefer,BCS)到玻色–爱因斯坦凝聚(Bose-Einstein condensation, BEC) 的渡越[24]、极化费米气体[25]、巡游铁磁等各种有趣的强相关系统[26]。自旋轨道耦合超流体是常见的时间反演不变的拓扑超流体。自旋向上的费米子配对为px+ipy态，自旋向下的费米子配对为px-ipy态。这类拓扑超流态在体系统里面有能隙，在材料边界上有相向传播的Majorana 费米子。

1956 年，人们首次提出库珀对来解释超导体[27]，它描述了一对费米子由于相互作用而结合在一起。费米子有相反的动量，所以这对费米子的动量完全为零。然而在强磁场中存在有限质心动量的库珀对，这导致了在实空间中具有不统一的序参量的奇异超导体，即Fulde-Ferrell 和Larkin-Ovchinnikov(FFLO)态[28,29]。FFLO态有两种: 相位调制的FF 态和空间调制的LO 态。在过去几年中，FFLO 态在实验和理论方面都引起了科学家的极大兴趣。自旋轨道耦合已经通过超冷原子和光晶格在实验上实现[30–33]，这为拓扑的FFLO 态铺平了道路。理论研究表明，在一维和二维费米气体中可以诱导出拓扑的FFLO 超流态，Majorana 费米子有可能存在于其中[34,35]。

同样地，拓扑超流体的实现和检测也是目前物理学最积极追求的目标之一。我们介绍了近几年的几种方法：在超冷40K 原子中观察通用束缚态的方案[36]、将原子加载到一个自旋相关的光晶格势中实现p 波拓扑超流体的方案[37]、研究超流3He 涡旋的方案[38]、使用杂质作为探针检测拓扑相变的方案[39]、还可以利用圆二色性来检测拓扑超流[40]。通过上述方法可以完成拓扑超流的实现与识别。

II. 光晶格中的拓扑超流

px+ipy超流态在拓扑量子计算中具有潜在的应用价值[41]。Liu 等人证明拓扑的px+ipy超流体相可以在单组分偶极费米气体中实现[42]。该气体被束缚在二维正方形光学晶格中，在低温下具有吸引相互作用。在偶极费米气体中，电偶极之间的各向异性相互作用在旋转电场的存在下可以转化为有效的吸引相互作用[43]。他们发现当相互作用较弱时，除了发生接近半填充的相分离外，p 波超流体对大多数填充因素都是稳定的[44]。在弱耦合极限下，相分离区域消失。填充系数为0 ＜n ＜1时，相互作用强度超过某一阈值时，系统将会发生相分离。

图1 展示了系统的零温相图。随着相互作用强度(J)的增加，相分离区域(PS)增大。在弱耦合极限J →0 时，相分离区域消失。在临界相互作用强度下，填充系数n=0 和n=1 之间发生相分离，化学势满足μ(0)=μ(1)，其中μ(n)为填充因子处的化学势，μ(0)=-4t，t代表跳跃幅度。由于粒子–空穴对称，μ(0)+μ(1)=V(0)，临界相互作用强度满足V(0) = -8t 和J = 0.89t。当相互作用强度超过临界值，即J ＞0.89t 时，系统变成n=0 和n=1 态的混合物，这是由于粒子或空穴密度为零而形成的绝缘态。

图1.零温度下的相图。实线为px+ipy 超流体相(p 波SF)与PS 之间的边界。PS 消失在弱耦合极限J →0。当J ＞0.89t时，超流相消失。引自文献[42]。

此外，三角光晶格在实验和理论方面也得到了广泛的研究。在三角光晶格中，外场和超冷原子间的不同类型的相互作用可以诱导出丰富的量子相[45–47]。Hao 等人提出可以通过有效的k3Rashba 自旋轨道耦合[48,49]、塞曼场和三角光学晶格中的s 波Feshbach 共振的共同相互作用来实现奇异手性f 波拓扑超流。其中，有效的k3Rashba 自旋轨道耦合和塞曼场是通过调制应用激光束产生的激光与原子的相互作用诱导的，束缚原子的超流态是利用s 波(Feshbach 共振)诱导的[50]。他们发现拓扑超流和常规超流体之间存在相转变，这是由块体间(能) 隙关闭机制[51]决定的。拓扑超流类似于具有f 波配对对称的常规超流[52]，这与三角光晶格的几何对称性一致。手性f 波拓扑超流在块体中是全能隙的，并且在边界上有三个无能隙的手性边缘态。更有趣的是，拓扑超流可以通过初始化激光器来调制。此外，拓扑超流中的每个涡旋上都有一个稳定的Majorana 费米子，而常规超流涡旋晶格结构与三角光晶格之间的兼容性对于研究Majorana 费米子的性质具有优势。因此，这些特性使得该系统成为执行拓扑量子计算的潜在候选系统。

图2(a) 展示了系统的能带结构。图2(b) 展示了当化学势位于μ4区域时，低能行为主要由哈密顿量和波矢主导，因此不能确定具体的手

性，他们将这些情况归因于常规超流。拓扑转变点由块体的能隙闭合条件决定：，如图2(d)，远离这一点的能谱是有能隙的。当表示有效塞曼场)，如图2(c)，在拓扑上常规超流是非平庸的，而当如图2(e)，在拓扑上常规超流是平庸的。根据上述分析，在图2(f)中给出了相图，结果表明，拓扑超流与初始参数任意相位φ 有很大关系。这意味着可以通过调制激光的参数来控制光纤的拓扑特性，这为研究拓扑超流提供了便利。

Liu 等人证明了周期性驱动的微扰可以引起从平庸超流到拓扑超流的相变[53]，这种相变在系统的边界上受拓扑保护并且是无能隙的。含时间周期的哈密顿量可以用Floquet 定理来描述，该定理可用于解释量化绝热泵浦现象[54]。研究表明，在一维Bose-Hubbard 模型中，超流体向Mott 绝缘体的相变可以由周期性驱动的光学晶格诱导[55]。他们将这种相变机制扩展到二维光学晶格的拓扑相变中，发现在周期性调制的光学晶格里，可以诱导从平庸超流到拓扑超流的拓扑相变。这种可承载Floquet Majorana 费米子的拓扑相被称为Floquet 拓扑超流[56,57]。还有人提出，在存在Rashba 自旋轨道耦合和大的垂直塞曼场相互作用的超冷费米原子的BCS型s 波超流体中，可以实现拓扑相[58,59]。然而，对于超冷费米原子来说，Rashba 自旋轨道耦合和大的垂直塞曼场很难同时实现[59]。研究证明如果用周期性驱动的光学晶格取代塞曼场[55]，自旋轨道耦合的BCS 型s 波超流仍然可以通过改变光学晶格的振荡幅度(或调制强度) 实现拓扑超流。因此，这提供了另一种产生可以容纳Majorana 费米子的拓扑超流的方法。

在图3(a) 中，质量M(z) 作为z 的函数，可以通过改变调制强度K 来调节，点B 是在M(z) = 0和z = 0.299 条件下能带E2和E3相互接触的地方。图3(b)～(d)展示了χ 方向上具有300 个点的几何条纹带结构，分别对应图3(a) 中A (z =0)、B (z =0.299)和C (z =0.4)。很明显，在质量M(z)＜0 的区域I 不存在边缘态。所以z ＜0.299 时，它是一个平庸的超流体。相反，在区域II 中存在一对边缘态。在z ＞0.299，且质量M(z)＞0 时，它是拓扑超流体。从普通超流体到拓扑超流体的相变发生在能隙关闭的B 点。

物质的拓扑态是一种特殊的量子相，通过块体–边界对应关系可以表现出不同的块体输运特性和边界输运特性。实验上已经发现了非相互作用费米子拓扑绝缘体，但是用玻色子实现的拓扑状态还不是很多。Liberto 等人发现由相互作用驱动的物质的拓扑态可能出现在充满超冷玻色子的Lieb 光晶格中[60,61]。因为系统的单粒子谱表现出明显的抛物线的带接触点，且两个带均表现出非负曲率。虽然系统在单粒子层面和相互作用基态上都不具有拓扑性质，但相互作用引起了激发态的反常霍尔效应，其陈数C 不为零。他们证明在现有的实验技术下，稳定的BEC 可以在这个高度对称的带接触点出现，它表现出宏观角动量，这样时间反演对称被打破，但是平移对称被保留了下来。这个相位在拓扑上是平庸的，但是，当Liberto 等人计算Bogolyubov 激发态时，发现能带结构表现出非相互作用系统所没有的拓扑性质[62–65]。

图4(a)显示了凝聚体的激发谱。由于U(1)对称破缺，频谱的最低分支变成了非简并的。Liberto 等人发现cn= 1 是频谱的最低分支，这个分支的Berry 曲率如图4(b) 所示。Berry 曲率的非零的k 空间轮廓类似于一个具有明确的时间反演对称性破缺的二次带接触点的自由粒子[60]。根本的区别是这里的时间反演对称破缺是突发的，并且是由相互作用驱动的。

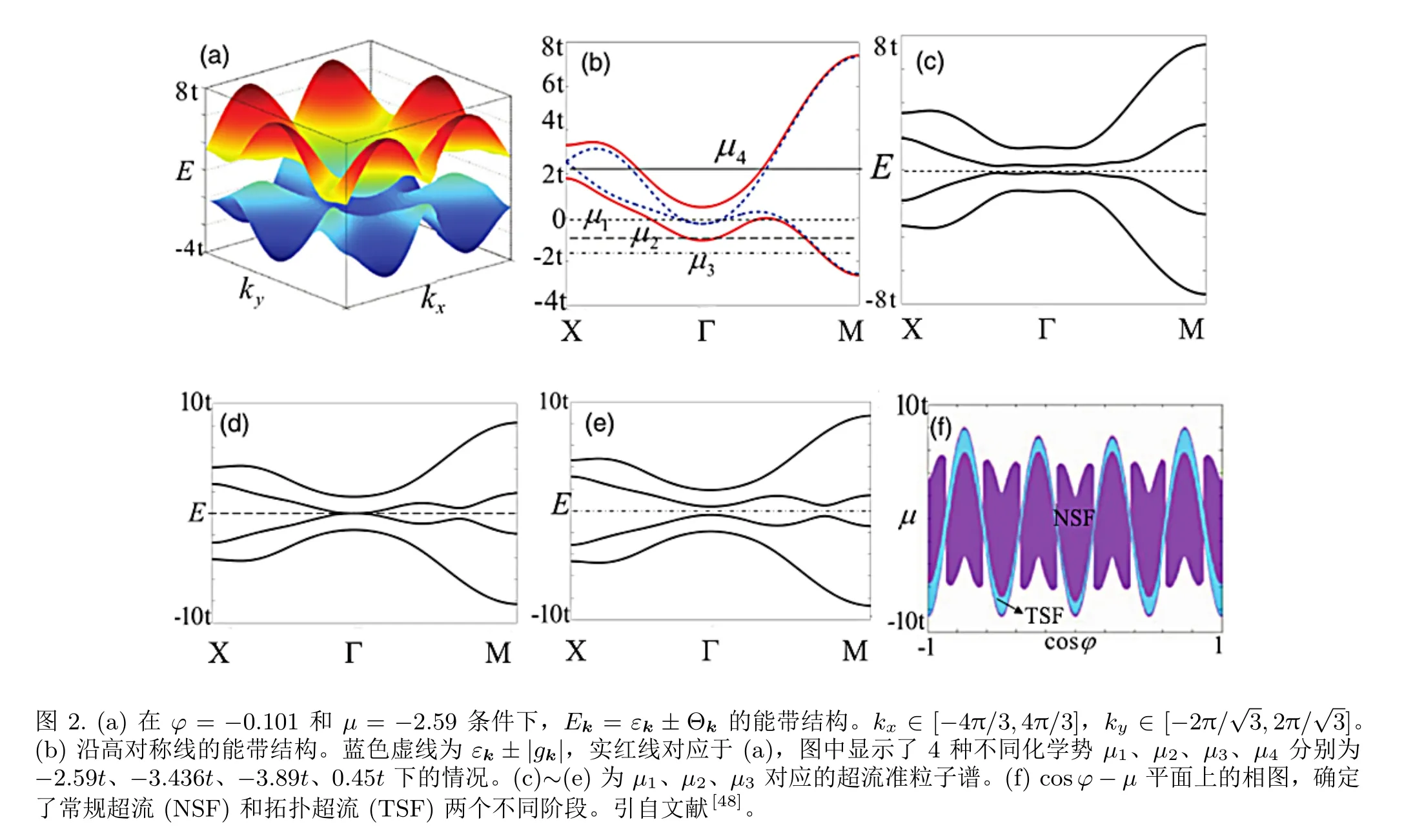
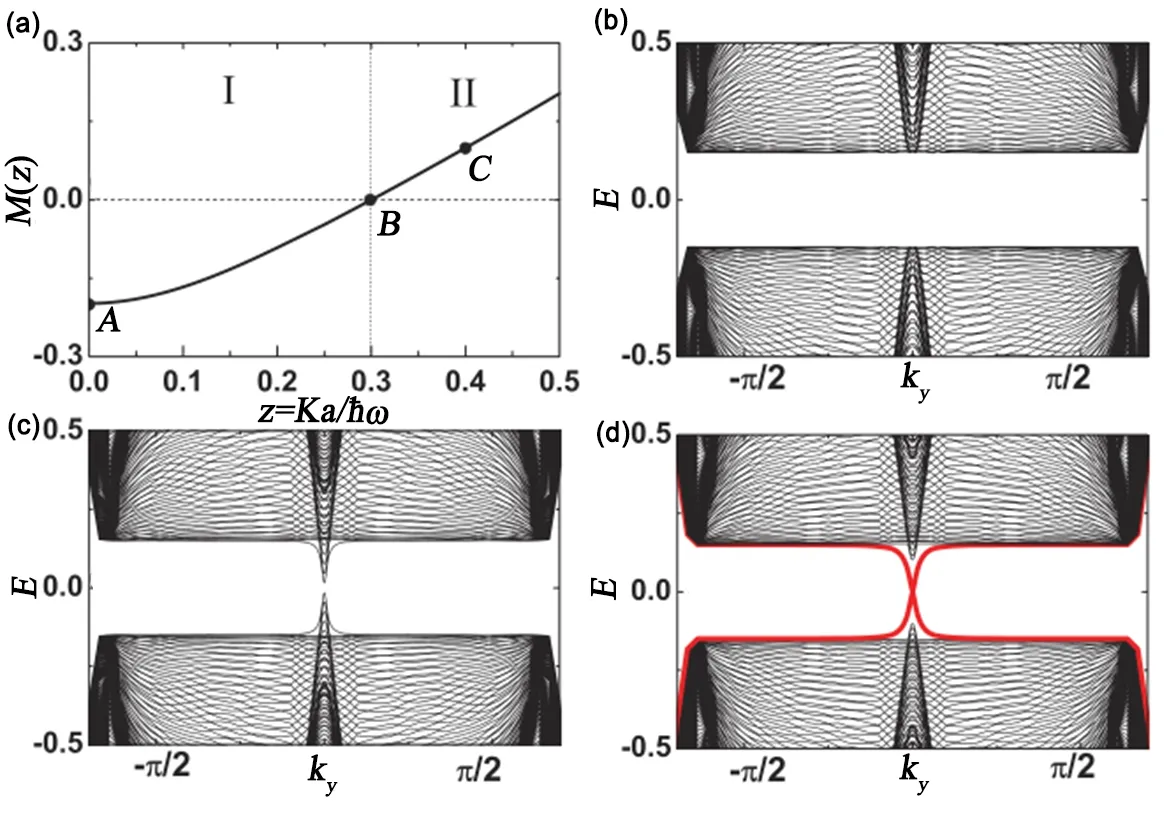
图3. 系统的相图和能带结构。(a) 质量M(z) 作为z 的函数，M(z) ＜0 的区域I 是平庸超流体，而M(z) ＞0 的区域II 是拓扑超流体。(b)～(d) ξ 方向上300 位的条纹几何中有效哈密顿量的能带结构，对应于(a) 中的A (z =0)、B (z =0.299) 和C (z =0.4) 点。引自文献[53]。

Lang 等人指出[66]，面心立方光晶格可通过三束激光的简单方案实现，这为在超冷原子中创建Weyl 点和拓扑节点超流体提供了一个高度可控的平台[67–72]。在非相互作用系统中，当振动这种面心立方晶格时，不需要复杂的隧道设计，在Floquet 带结构中会自动出现Weyl 点。在两个超精细自旋态之间存在吸引相互作用的情况下，并且经历相同的振动面心立方晶格，将会出现一个三维拓扑节点超流体，Weyl 点显示为准粒子谱中的无能隙点。在面心立方光晶格系统中可以创建一个电荷数为2 的双Weyl 点，或者将其拆分为两个带电荷数为1 的Weyl 点，可以通过调节相互作用使Weyl 点在动量空间中移动。相应地，表面上的费米弧[73]可以相互连接，也可以作为单独的弧分开。

非相互作用系统中Weyl 点的一个特征是表面存在费米弧，它是一条零能态的未闭合线。然而，在没有相互作用的情况下，系统中能观察到如图5(a) 所示的费米弧。当节点超流体出现时，探索相互作用的情况更有趣。求解半填充自恰的Bogoliubov-de Genne(BdG) 方程，在半填充自洽(100)表面上ky和kz仍然是好的量子数，并且零能表面态如图5(b) 和5(c) 所示。在面心立方光晶格中引入两个超精细自旋态，每个超精细自旋态都具有相同的单粒子哈密顿量。这对应于一个自旋无关的振动晶格，在动量空间的相同位置有两个手性相同的Weyl 点。在没有相互作用的情况下，如果化学势正好调节到Weyl 点，多体基态将只由两个相同的Weyl半金属组成[67–72,74]。与电子自旋不同，超细自旋在超冷原子中是守恒的，在单粒子能级中会产生两个为1 拓扑电荷，如图5(d) 所示。

假设在围绕布里渊区的每个Weyl 点的有限费米曲面上打开一个相互作用，每个费米面上将会有一个点保持无能隙，而超流体能隙在其他任何地方会打开，如图5(e) 所示。出现的三维节点超流体是一种拓扑超流体，这从准粒子谱中节点所携带的拓扑电荷可以看出。在图5(e) 和5(f) 所示的这两个Weyl 点附近，色散沿三个方向呈线性。由于非相互作用系统围绕k 轴具有四重旋转对称性，这样的分裂使对称性降低为二重对称，分裂方向是kx-ky平面内任意方向的自发对称性破缺的结果。通过改变相互作用强度，这两个Weyl 点会在布里渊区中移动。对于非相互作用系统，调整参数会导致Weyl 点的运动而不会打开能隙。另外，调节相互作用也为控制布里渊区中Bogoliubov 准粒子谱中的Weyl点提供了机会。

高阶拓扑超流体存在有能隙的块体[75–77]，并具有不同局域化的受对称保护的Majorana 零模。Wu 等人研究了一种合成多阶拓扑超流体方案[78]，这种超流体在超冷原子气体中可以支持各种Majorana 零模。在二维光学超晶格中可以诱导一个受空间调制的自旋轨道耦合，这给高阶拓扑态提供了额外的自由度。研究发现了拓扑平庸的超流体，包括一阶和二阶拓扑超流体，以及在实验可调参数下的不同的拓扑相变。在该系统中不仅发现了与块体能隙闭合和重开相关的陈数特征的转变，还发现了可以支持具有Majorana 角模的拓扑超流体[79–81]，但拓扑相变经历了没有体带的能隙闭合。相反，这种相变是通过边缘态的能隙闭合发出信号的。该方案基于s 波的相互作用，结合了一个简单的真实系统中的多阶拓扑相变，并利用现有的实验技术得到了验证。

在图6(a)中，研究发现了两个符号相反陈数的一阶拓扑超流区域。其中存在陈数C =0 和四极矩qxy=1/2的理想二阶拓扑超流相，并且该相通过一阶拓扑超流区域与普通超流相隔离。在图6(b) 中，研究了相互作用对相变的影响。当相互作用强度U 超过阈值时，系统转变到超流相。除了传统的一阶拓扑超流相变外，还发现系统经历了从平庸的超流相到二阶拓扑超流相的直接转变，在此过程中C 仍然为零，但qxy发生了变化。相图表明，二阶拓扑超流相的拓扑不变量由qxy代替，所以相变不能只由C 来描述。图6(c) 展示了化学势对系统的影响，由于序参量引入了粒子对称性，相图相对于μ=0(即半填充) 是对称的。在大的塞曼场Vz下，近半填充系统的单粒子性质表现为带状绝缘体[82]，超流相在μ ≈±2t 范围内坍塌，费米超流体的存在被明显抑制[83]。

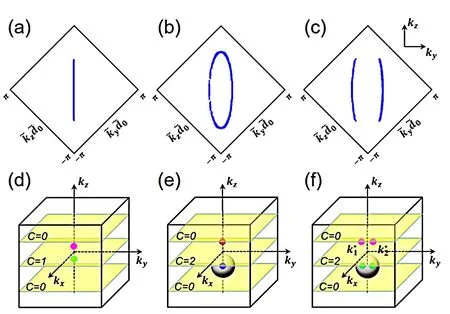
图5.(a)具有自旋向上或自旋向下的非相互作用单粒子表面的费米弧。(b)和(c)Bogoliubov 准粒子(半填充)的费米弧。(d)～(f)没有交互、只有一个交互和两个交互的整体节点示意图。粉(绿) 点和红(蓝) 点分别为+(-)1 和+(-)2 电荷节点。(e) 和(f)中包围节点的球体最低两个波段具有相同的总陈数-2。引自文献[66]。

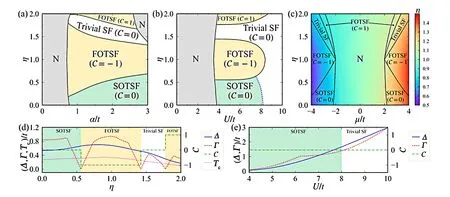
图6.(a)～(c)在(a)α-η、(b)U-η、(c)μ-η 平面的相图。在相图(a)中设置(U,μ)=(6,3t)，在相图(b)中设置(α,μ)=(2t,3t),在相图(c)中设置(α,U)=(2t,6t)，在所有相图中设置Vz =2t 和δμ=0。平庸的SF 和N 分别代表平庸的超流体和正常的气体相。黑色实线(蓝色虚线)对应的相位区域与(没有)块体能隙关闭区域的边界。相图(c)中的颜色代表了填充因子的特征。序参量Δ(蓝色实线)、块体能隙Γ(红色虚线)和陈数C(绿色虚线)作为(d)η 和(e)U 的函数。设置图(d)中(α,U,Vz)=(2t,6t,2t)和图(e) 中(α,η,Vz)=(2t,0.33,2t)。在图(d) 中用红色虚线表示临界温度Tc。引自文献[78]。

Wu 等人发现即使在有限温度下，超流相也可能存在。图6(d) 展示了BdG 方法下超流相的临界温度Tc。跳跃幅度在紧束缚近似下通常为0.1Er量级。由于反冲能量ER～(π/3)2/3EF[84]，并且Tc(≈0.3t) 的级数为0.1EF。因此，以目前的实验技术，超流相有望在T ～0.05EF下存在[85,86]。现有的拓扑相变的特征依赖于块体边界对应，但表现方式不同。为了研究拓扑相变的基本性质，还绘制了能隙Γ 和陈数C 的曲线。通过改变η，能隙会在不同拓扑相之间的转变处关闭和重新打开。这与传统的物理图像是一致的，即在体隙闭合和陈数改变的同时发生拓扑相变，拓扑相变是已知一阶相变，并且服从明确的块体边界对应关系。在一阶拓扑超流中，除非体隙关闭，否则边缘态总是会受到拓扑保护。而在图6(e) 中，在二阶拓扑超流相到平庸相的非常规相变过程中，通过改变相互作用强度U、序参量Δ 和块体能隙Γ 将在此过程中单调增长。

III. 自旋轨道耦合诱导的拓扑超流

Zhou 等人研究了二维的自旋轨道耦合费米气体[87]，在二维空间中，只存在一个总是受到远离其相边界的激发能隙保护的非平庸拓扑超流相[88,89]。当在这一阶段产生涡旋时，在其中心就会出现Majorana 零模。由于粒子数不平衡和配对之间的竞争，在一个外部势阱中，不同的相会出现在不同的位置。研究的相图表明了在局域密度近似下宽Feshbach 共振附近典型势阱中的相分离结构，以及势阱中存在稳定拓扑超流相的参数区域。Zhou 等人使用不同相的动量空间密度分布来表征不同相的性质。值得注意的是，少数自旋的动量空间密度分布在拓扑超流体状态的原点附近具有下降的特征。对于拓扑超流态能全部占据势阱中心的参数，动量密度分布下降的特征可以保留在飞行时间成像过程中，从而为拓扑超流态提供一个明确的信号。

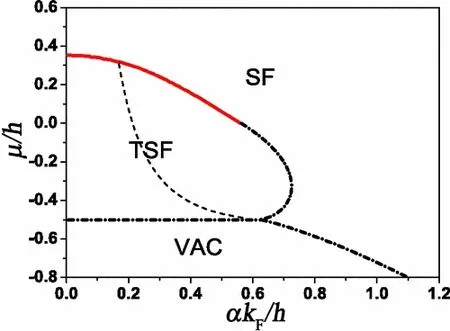
图7. α-μ 平面上的相图，一级相变用实心(红色) 曲线表示，二级相变用虚线(黑色) 曲线表示。拓扑超流区域的细虚曲线标志着Δ/h=10-3 的阈值。引自文献[87]。

从图7 中可以看出拓扑超流相似乎具有明显的稳定区域，然而这可能会误导实验检测。实际上，在自旋轨道耦合强度较小的拓扑超流相中，配对能隙通常是微乎其微的。这可以从图7 中穿过拓扑超流相的虚线看出，该虚线由能隙方程通过设置Δ/h=10-3求解得到。在虚线的左边，配对能隙Δ/h ＜10-3，且随着α 趋近于零呈现指数衰减。只有当α 进一步向拓扑超流和常规超流的相边界增加时，序参量Δ 才会变得显著。在实验上，考虑到二维系统在有限温度下的波动，只可能在虚线的右侧观测到具有大的配对能隙Δ 的拓扑超流相。图7 还提供了势阱相分离结构的信息，当自旋轨道耦合较小时，费米气体相分离为两个区域：一个具有大的自旋极化和极小的配对序参量的拓扑超流相包围了一个常规的超流相，拓扑超流相与常规超流相之间是一级相边界。随着自旋轨道耦合的增加，拓扑超流态和常规超流态对应的热力学势的局部极小值随着拓扑超流态的配对能隙的增大而减小。两个局部极小值在临界点合并，超过临界点后，拓扑超流和常规超流之间的相边界变为二阶。进一步增加自旋轨道耦合，可能会有一个拓扑超流相在势阱中以环形结构出现的参数区间。最后，当自旋轨道耦合足够大时，不再发生相分离，势阱中充满了Rashbon 超流体[90]。

图8 展示了系统的壳体结构。拓扑超流相通常出现在势阱的边缘或两个常规超流相之间的环上。值得注意的是，在一些参数区域，拓扑超流态可以占据整个势阱。如图8 中最右边的一列所展示的，对应于α-μ 平面相图中以拓扑超流相为起点的一条垂直线。只有当总极化超过一个临界值时，拓扑超流相位才会占据整个势阱。这为检测势阱气体中的拓扑超流态提供了理想的条件。当极化P 从临界值减小时，常规的超流相将出现在势阱中心，并逐渐延伸到势阱边缘，最终会在较小极化的情况下占据整个势阱。此外还存在一个参数区域，此区域中势阱只被拓扑超流相所占据。在这种情况下，动量分布中拓扑超流态的特征可以在势阱中存活，使信号在飞行时间成像过程中可被检测到。

同时 Yi 等人研究了在均匀和势阱情况下三维Rashba 自旋轨道耦合费米气体的零温度相图[91]。与二维情况下不同的是，在三维的情况下，准粒子激发谱中有两个不同的拓扑非平庸相，分别存在两个或四个无能隙点[92,93]。对于均匀气体，相分离态的稳定区域更大。此外，他们发现自旋轨道耦合不仅能诱导出由正常和常规超流相组成的典型相分离态，还能诱导出包括拓扑上非平庸的无能隙超流在内的更复杂的相分离。他们的研究表明了不同的相分离以及无能隙超流相、常规超流相和正常相的稳定区域。中等强度的自旋轨道耦合能稳定独特的无能隙相，而对于足够大的自旋轨道耦合，系统总是Rashbon 常规超流体。研究展示了如何通过不同的激发谱和动量空间密度分布来表征这些相。这项工作通过研究各相的稳定区域，证明了存在势阱时观测拓扑上无能隙超流态的最佳参数区域。

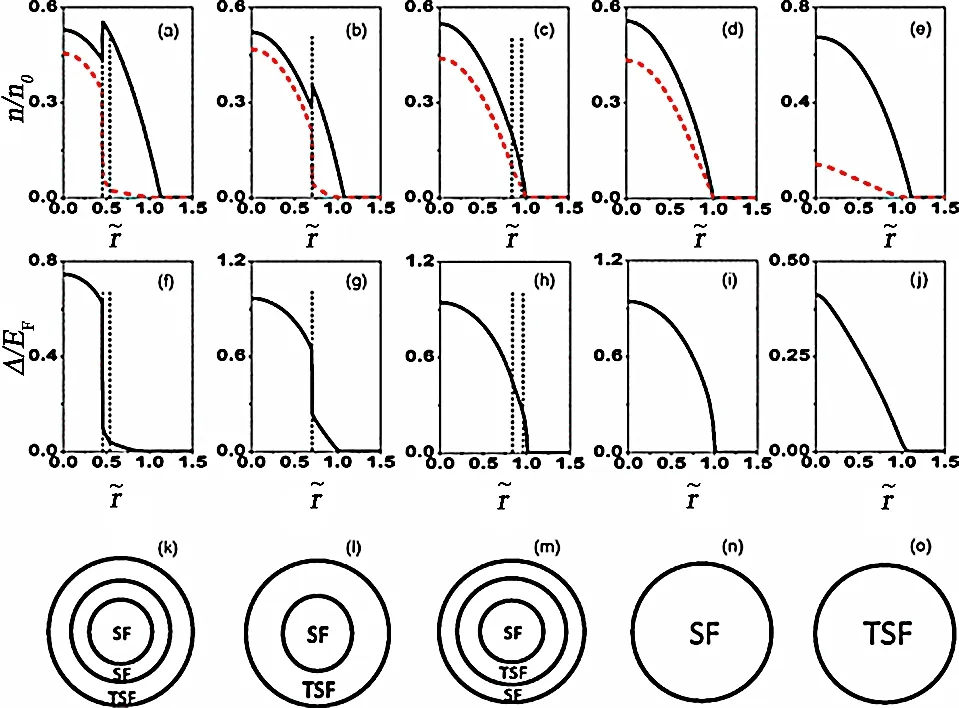
图8. (a)～(e) 粒子数密度的分布。(k)～(o) 相分离的壳结构。密度子图中的实黑色(红色虚线) 曲线表示自旋向上(自旋向下)的部分。(a)～(j) 中的细虚线表示拓扑超流–常规超流或常规超流–常规超流边界。引自文献[87]。

图9 表明当自旋轨道耦合关闭(α = 0) 时，系统在通过一级相变成为正常态之前，仍处于正常和常规超流(PS1) 的相分离态(P ≈0.93)。随着自旋轨道耦合强度α 的增加，出现了丰富的相结构，如有能隙的常规超流相、无能隙的超流相(GP1 和GP2) 以及不同的相分离态。这些相分离态被一级相变的相边界所分开(图9 中粗体曲线)。除了典型的PS1 阶段外，现在还存在一个具有四个无能隙点的超流和常规超流的相分离态(PS2)，以及两个不同的具有四个无能隙点的超流的相分离态(PS3)。随着α 的增加，对于中间的P 和α，系统会发生从PS1 到PS2 再到PS3 的二级相变。

为了理解势阱中各相的空间分布，他们还给出了α-μ平面上的相图(图10)。在局域密度近似条件下，假设两种自旋物质具有相同的简谐势，局域化学势μ(r)可以与势阱中心的化学势μ 相关联，即μ(r)=μ-V(r)，其中V(r)为阱势。因此，图11 中一条向下的垂直线表示从势阱中心到边缘的轨迹，势阱中心的化学势由该线起点的化学势所确定。在图10 中四个无能隙点的超流相与图9 一致，只存在于势阱的一个小参数区域，而具有两个无能隙点的超流相似乎有相当大的稳定区域。当α 较小时，势阱中的费米气体将相分离为位于核心的常规超流相和正常相。

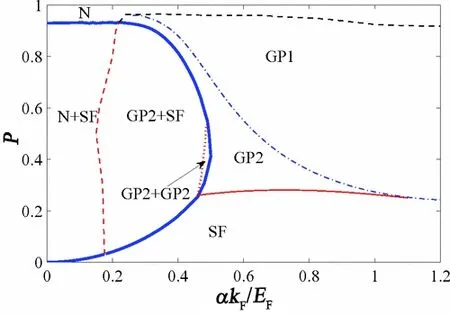
图9. 在(αskF)-1 = 0 处具有种群不平衡的均匀费米气体的零温相图。在粗的相边界内是不同的阶段分离状态。这些相分离状态可以通过一阶相变与非相分离状态相连接(实心粗体曲线)。细曲线表示各种二阶相变。引自文献[91]。

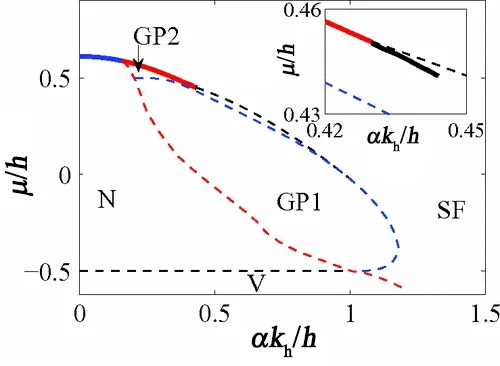
图10. 当(αskF)-1 =0 时，在(μ/h,αkh/h) 平面上的相图。二阶相变为细虚曲线，一阶相变为实心粗曲线，在热力学势双阱结构消失时结束(插图)。真空的边界(V) 是通过设置大多数自旋物质的化学势在正常相中消失而确定的。引自文献[91]。

He 等人研究了已经在实验中实现了的由一维耦合线和一维自旋轨道耦合组成的三维光学立方晶格系统[30–32,94,95]。其中每一根一维导线都具有形式为kxσz的自旋轨道耦合，kx表示沿导线方向的动量，σz表示粒子自旋。这些导线通过简单的跳跃进行耦合，从而保持粒子的自旋。然而在具有吸引相互作用的情况下[96,97]，系统会进入具有节点环的拓扑超流态。由于节点环的存在，在表面布里渊区存在大量具有零能Majorana 模的Majorana 腔。这里所发现的节点环完全固定在费米能量处，并且与其他能带很好地隔离。此外，大量的Majorana 模态因受手性对称的保护而保持在零能态。研究表明可以通过打破手性对称性来打开大部分节点环，使系统成为具有节点和手性Majorana 模的Weyl拓扑超流。通过引入形式为kxσz+kyσx+kzσy的三维合成自旋轨道耦合能进一步降低晶格对称性，Weyl 超流态中的Weyl 节点会在能量上发生位移，从而出现涡旋的Majorana 边缘态。

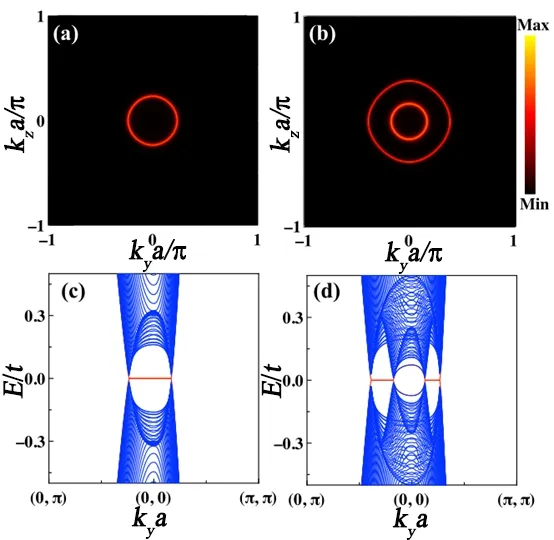
图11. 超流相中的环状节点。在kx =0 平面上，超流体的零能谱函数表现为单环节点(a) 和双环节点(b)。沿着表面布里渊区(kya,kza) = (0,π) →(0,0) →(π,π) 的路径，绘制了单环节点的准能边谱(c) 和双环节点的边界能谱(d)。平坦能带中的态构成表面Majorana 腔。引自文献[37]。

拓扑节点环超流体受到手性对称性的保护。当引入自旋轨道耦合项的另一组分kzσy形成二维合成自旋轨道耦合时，手性对称性被破坏。在kx=0 的平面上，对于非零kz，新的自旋轨道耦合场kzσy使原子自旋在k 和-k 上向相反的方向对齐，从而形成库珀对。而在kz=0的平面上，自旋轨道耦合场的消失导致了配对能隙的消失。结果表明，新的自旋轨道耦合场提高了环节的简并度，而点节保持原来的简并度。此时拓扑节点环超流进一步驱动到Weyl 超流，如图12(a)所示。在二维自旋轨道耦合超流相中形成的Weyl 节点是非常稳定的，除非由于强干扰，相反手性的Weyl 节点之间发生相互湮灭，否则无法移除Weyl 节点。弱干扰只能在动量和能量空间中转移Weyl 节点。当二维自旋轨道耦合演化为三维合成自旋轨道耦合(kxσz+kyσx+kzσy) 时，也就是所谓的Weyl 自旋轨道耦合[98–100]，BdG 准粒子能谱中的Weyl 节点会转移到不同的能量，如图12(b)所示。在表面布里渊区，Weyl 点由Majorana 弧连接，如图12(c)所示。自旋轨道耦合场在ky方向上将Weyl 节点转移到不同的能量。因此，连接手性相反的两个Weyl 点之间的Majorana 弧得到了一个有限斜率，如图12(d)所示。

此外，拓扑超流的概念得到了扩展，包括了一类新的无能隙Majorana 边缘态的拓扑相，称为高阶拓扑超流相[75,101–103]。二阶拓扑超流是一个在(d-1) 维边界上具有拓扑非平庸能隙的d 维系统，这样在(d-2)维边界上就存在受保护的低能模。换句话说，一个二维的二阶拓扑超流有Majorana 角态，即束缚在两个边界相交处的Majorana 费米子。人们在近似诱导系统中，已经提出了一些关于实现二阶拓扑超流的理论实验设置，包括生长在铜超导体或s±波铁基超导体上的二维拓扑绝缘体[104]，放置在时间反演不变p 波超导体[105]上的铜氧化物超导体或Rashba 半导体和夹在两个铁基超导体FeTe0.55Se0.45[105]之间的铜氧化物超导体。

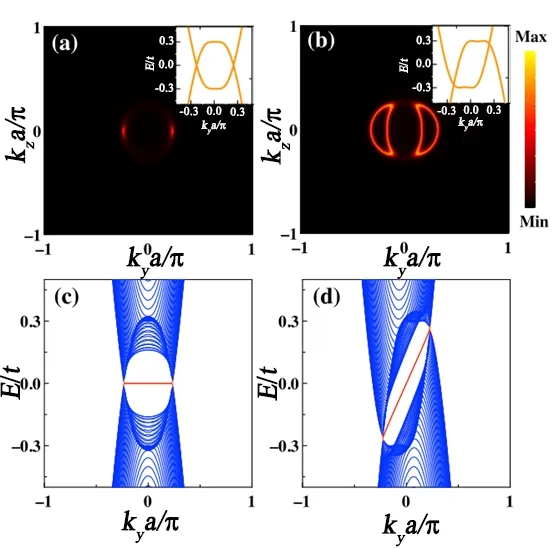
图12. 在超流相中，Weyl 点由单环节点演化而来。在kx =0平面上绘制了(a) 具有相同能量Weyl 点的Weyl 超流体和(b) 具有能量位移Weyl 点的Weyl 超流体的零能谱函数。图(a) 和(b) 中的插图对应于穿过Weyl 节点的块体能谱。在表面布里渊区，鼓膜状的Majorana 边缘态被还原为Majorana 弧。图(c) 中Majorana 弧是能量相等的Weyl节点之间的平坦带，而当Weyl 点能量转移时，它支持图(d)中单向的Majorana 弧。引自文献[37]。

虽然人们已经提出了一些可能的二阶拓扑超流系统，但是这些模型中的配对是非常规的[104,105]。超冷原子间的相互作用通常作用在s 波通道内，因此，出现了一个问题: 是否有可能通过控制单粒子能带结构，在具有s波相互作用的超冷费米气体中设计二阶拓扑超流？一般来说，控制单粒子的能带结构应该比直接控制复杂的配对容易。Huang 等人提出的模型可以体现在两层间自旋轨道耦合沿ky(kx)方向存在π(0)相位差的超冷费米子气体的双层模型上[106]，并展示了受新兴镜像对称保护的能隙拓扑超流。这种受镜像对称保护的拓扑超流体意味着存在镜像反射不变边界上的Majorana 零模，而在其他边界是有能隙的[107,107,109,110]。考虑一对有能隙的边界，它们是变量，但在镜像反射下相互映射。块体的拓扑非平庸性保证了这些边界上镜像对称破缺的质量项是唯一的，并表现出符号相反的能隙[102,104]。因此，这对边界的交点对应一个域壁，导致了Majorana 角态能够实现二阶拓扑超流。当系统旋转时，这些Majorana 角态也具有鲁棒性，因此不再存在任何与镜像相关的边界[102,104]。

图13 中展示了在镜像对称的情况下，当θ = π/4时，沿x 和y 方向相互映射的边界。对于有能隙的拓扑相，块体的镜像拓扑保证了指定的边缘态是有能隙的，并且这些边界上的镜像对称破缺质量项表现出符号相反的能隙[102,104]。因此，这些边界的交点对应一个域壁，自然导致了Majorana 角态。图13(a) 和13(b) 展示了Majorana 角态在拓扑能隙相对应的能谱和波函数。与有能隙拓扑相类似，ky′= 0 的边缘态在有四个狄拉克点的无能隙相中也是打开的。但边界上Majorana 平坦带的存在使得相关能谱，如图 13(c) 所示，显示除Majorana 零模之外的一系列低能态。这些低能态直接导致Majorana 零模渗透到系统内部，如图13(d) 所示。其他所有无能隙相的能谱和对应的波函数也绘制在图13 中，并显示了与具有四个狄拉克点的无能隙相一致的结论。然而对于具有两个狄拉克点的无能隙相，低能态数相对较少， Majorana 零模的渗透并不严重。定性地说，低能态的数量与动量空间中Majorana 平坦带的总宽度一致。这说明两个狄拉克点的无能隙相中具有少量的低能态。

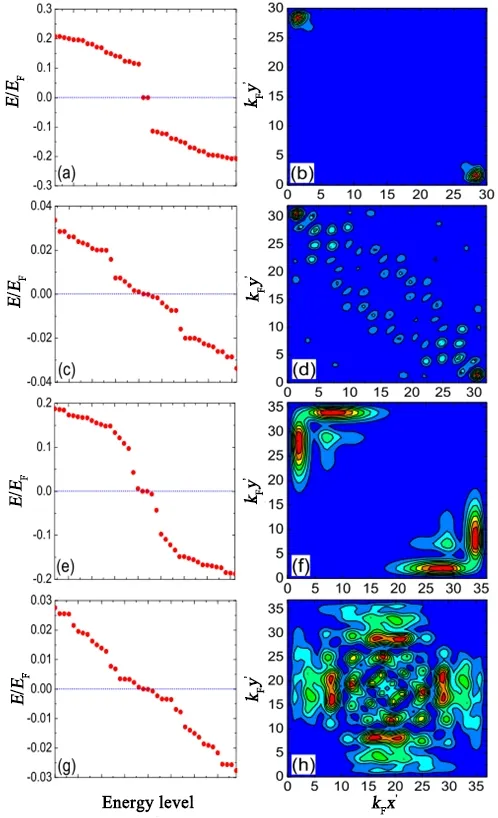
图13.0d 边缘态光谱和Majorana 零模的波函数。在θ =π/4时，其边界沿x′ 和y′ 方向镜像对称下相互映射。引自文献[106]。

IV. 拓扑FFLO 超流

Cao 等人预测了二维自旋轨道耦合费米气体中具有非均匀 Fulde-Ferrell(FF) 配对的无能隙拓扑超流体[111]，该超流体在块体中具有无能隙激发态，并且在边界处存在非阿贝尔Majorana 费米子。它在有限温度的条件下存在于广泛的参数范围内，不需要特定形式的自旋轨道耦合，因此可以在冷原子实验室进行实验观察。块体无能隙激发态会导致系统拥有更丰富的热力学和动力学性质。他们的工作可能为探索冷原子和固态系统中的拓扑物质提供新的见解[31,32,112]。

图14 为ΩR-δ 平面上Rashba 自旋轨道耦合二维费米气体的典型低温相图。文献中[36,58,88]对零平面塞曼场(δ =0)的情况进行了很好的探讨。平面外的磁场ΩR驱动了拓扑相变。ΩR的增加不仅通过打破时间反演对称性和打开自旋轨道能隙改变了两个螺旋度分支色散关系的拓扑，还在低螺旋度分支中诱导了有效的p 波费米子配对[88]。因此，有能隙拓扑超流体不断出现在阈值上方。与此拓扑相变相关联，系统的能隙将首先在ΩR,c精确闭合，然后立即重新打开。非零但很小的平面内磁场的存在不会改变这一图像，但由于低螺旋度分支[58]中的费米面变形，这有利于有限动量的FF 配对。因此，出现了一个有能隙的拓扑FF超流体。

图14. 二维Rashba 自旋轨道耦合费米气体在Eb = 0.2EF、λ=EF/kF 和T =0.05TF 条件下的低温相图。通过调整平面外和平面内的塞曼场ΩR 和δ，系统可以从有能隙FF (gFF)演化为节点FF (nFF)，然后是无能隙的拓扑FF(tnFF)，最后是有能隙的拓扑FF (tgFF)。在点虚线之上，序参量Δ 小于0.001EF(因此表示为正常阶段)。虚线表示达到临界Berezinskii-Kosterlitz-Thouless(BKT) 温度的边界。在两者之间，伪能隙区域由阴影区域突出显示。引自文献[111]。

然而值得注意的是，在足够大的面内塞曼场条件下也会出现无能隙的拓扑FF 超流。在这种情况下，增加ΩR会使得费米气体首先到达到无能隙状态，最终变成有能隙的拓扑超流体，如图15(a) 所示。图15(b) 展示了在无能隙状态下，较低螺旋度的粒子分支的能量在距离原点k = 0 稍远的一小块区域内小于零。图15(c) 展示了的节点在动量空间中形成两个不相交的环，但在临界值ΩR处，两个环在k =0 处连接。在此条件下，费米面的拓扑结构发生了变化，意味着出现了无能隙拓扑FF 超流体。

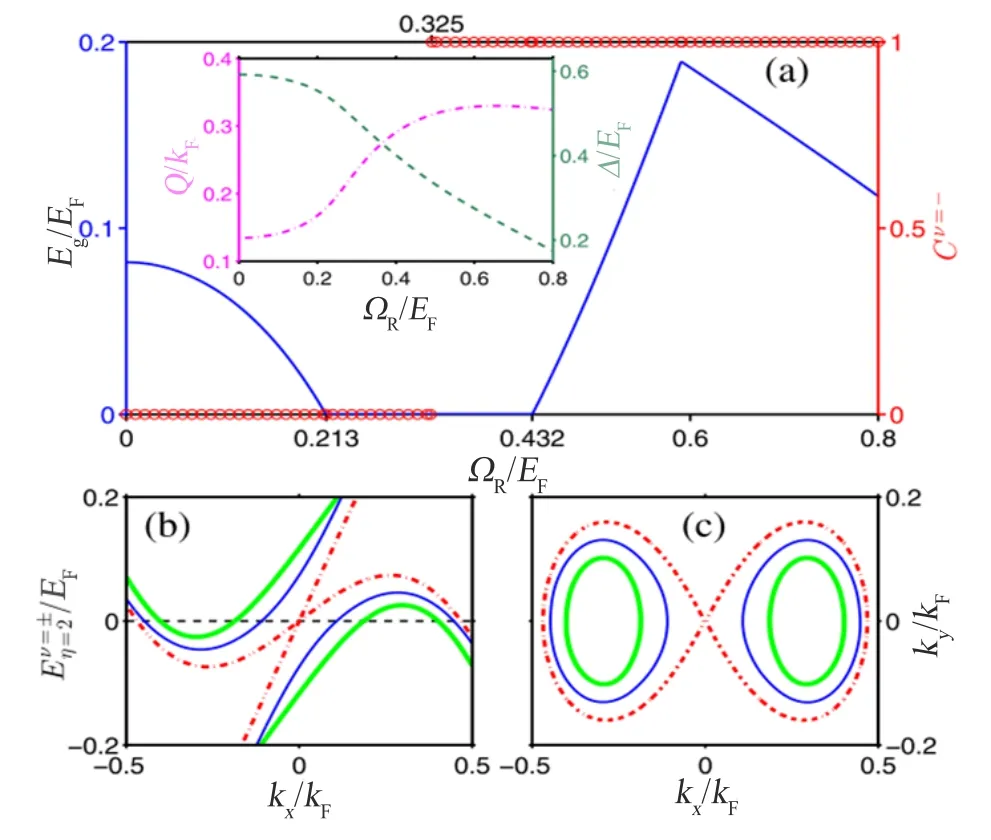
图15. (a) 当δ = 0.4EF 时，最小激发能隙Eg 和陈数随着ΩR 增加时的演化。插图展示了FF 配对动量和配对能隙Δ的演化过程。(b)低螺旋度分支的色散关系：Eνη=2(kx ky)=0在ΩR/EF = 0.24(绿色粗线)，ΩR/EF = 0.325(红色虚线)，ΩR/EF = 0.38(蓝色细线) 经过的拓扑相变。(c) kx-ky 平面上对应的零能谱(节点) 等值线。引自文献[111]。

Zhang 等人提出如果FF 超流体具有有能隙的块体准粒子激发和拓扑的非平庸费米面这两个关键元素[35]，它就可以支持Majorana 费米子。这些新的量子态是拓扑的FF 超流。在这种情况下，由传统的大塞曼场诱导的无能隙FF 态不属于这一类。在这里，他们提出了一个使用二维(2D) 或一维(1D) 自旋轨道耦合的简并费米气体实现拓扑FF 超流体的方案，该气体受面内和面外塞曼场的影响。自旋轨道耦合简并费米气体与一个面外塞曼场能支持零动量配对的Majorana 费米子[21,113–115]。在适当的参数区域内，平面内塞曼场可以诱导有限动量配对的Majorana 费米子[116–119]，还能同时保持超流体的激发能隙以及其费米面的拓扑。拓扑FF 超流的区域不仅取决于化学势和配对强度，还取决于Cooper 对的自旋轨道耦合强度、总动量和有效质量，以及塞曼场的方向和大小，从而大大增加了实验的可调性。最后，他们还讨论了该方案在半导体/超导体异质结构中的潜在应用。

完整的相图如图16 所示。由于Qy和hx两者具有相同的符号，相图在hx-hz平面上表现出完全对称。随着自旋轨道耦合强度的增加，拓扑FF 相通过膨胀到正常相而大大增大。对于小的自旋轨道耦合，见图16(a)，总是需要一个有限的hz来诱导拓扑FF 相。图16(b)展示了存在一个有趣的参数区域，可以通过一个极小的hz在hx～0.8EF附近实现拓扑FF 相。然而，在hz=0时，从Berry 曲率和陈数可以分析得出永远不可能在此条件下观察到拓扑FF 相。从图16(a) 和图16(b) 可以看出，拓扑能隙FF 相在数学上可以看作是拓扑BCS超流在平面内塞曼场作用下的绝热变形，但是它们的物理意义完全不同。在图16(c) 与16(d) 中，可以发现在较小的结合能和较小的hz下能够观察到无能隙FF 相，而在足够大的结合能下，系统可以是拓扑或非拓扑能隙相。在这种情况下，其中μ ～EF-Eb/2，Δ2～2EFEb，因此hz∝Eb，这需要关闭和重新打开Eg。

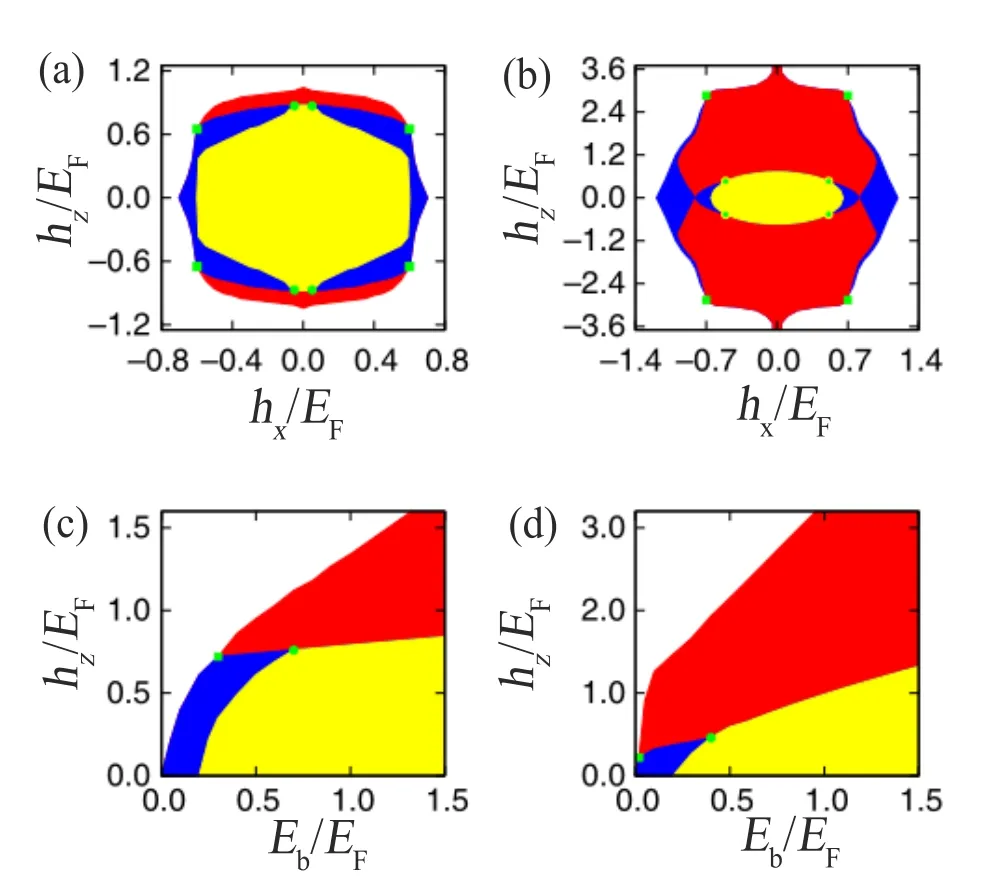
图16. FF 超流体相图。用不同的颜色标记不同的相: 拓扑有能隙FF 超流体(红色)、非拓扑有能隙FF 超流体(黄色)、无能隙FF 超流体(蓝色) 和正常气体(白色)。其他参数有：(a)Eb =0.4EF，αkF =0.5EF；(b) Eb =0.4EF，αkF =1.0EF；(c) hx = 0.5EF，αkF = 0.5EF 和(d) hx = 0.5EF，αkF =1.0EF。每个图中的记号都是三临界点。引自文献[35]。

图16 中用符号标记的三临界点对于理解相图的基本结构至关重要。沿着hz轴，系统只支持能隙BCS 超流体(拓扑或非拓扑)和正常气体[115]，而沿着hx轴，系统只支持平庸的FF 超流体和正常气体[117–119]。因此，拓扑BCS 超流体与平庸FF 相之间不可能存在绝热联系，需要有一些点来分离不同的相，而这些点这正是三临界点。在他们的模型中，不同阶段之间的相变是一阶相变。这里存在的三临界点应该与同一系统中有限温度下没有自旋轨道耦合的三临界点形成鲜明的对比，后者是由一阶和二阶相变线的偶然相交[121]引起的。因此，虽然图16 中的三临界点的具体位置会随着系统参数的变化而变化，但它们是不会被移除的。

他们提出的拓扑FF 相可以用半导体/超导体异质结构实现。这种异质结构已经用于实现拓扑的BCS 超导和相关的Majorana 费米子[58,88]，并且已经能观察到一些初步的实验特征[122–124]。由于FF 态可以在大磁场下存在，这可以为实验上使用许多具有大自旋轨道耦合但小g 因素的半导体纳米线(例如GaSb、空穴掺杂InSb 等) 提供了可能性。

Wang 等人探讨了受自旋轨道耦合影响的费米气体的拓扑超流体特性[125]，其中自旋轨道耦合是使用玻色子原子的双层方案产生的[126,127]。双层系统的一个特点是，相互作用主要发生在属于同一层[126]的原子之间。因此，原子–原子相互作用与自旋轨道耦合方案中涉及四个循环耦合原子内部状态的相互作用有很大不同[128]。在后一种情况下，四种内部状态的原子相互作用的强度大致相同。他们发现双层方案提供了一个有趣的超流体相变，在不是很强的原子光耦合下，出现了FFLO 态[129]。一般来说，FFLO 态出现在自旋极化系统中，也可以由自旋轨道耦合费米气体中的面内塞曼场诱导[34,35]。他们发现对于不是很强的原子光耦合，FFLO态本质上出现在没有任何外部磁场或自旋极化的双层系统中。随着原子光耦合的增加，系统会从FFLO 态转变到拓扑超流态。他们的这项工作证明了拓扑超流也可以出现在实验可行的双层体系中。

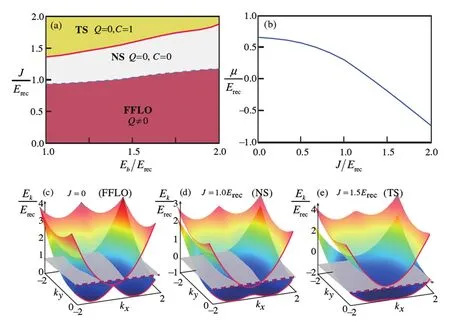
图17. 在Ω =J 和φ=0.6π 条件下的相图。(a) 中红色区域为FFLO 态，对应于Q／=0(Q 为动量空间的有限配对中心)，灰色区域为平庸超流态(NS)，对应于Q=0 和C =0，黄色区域为拓扑非平庸态(TS)，对应于Q=0 和C =1。(b) 随着耦合强度的增加，化学势单调减少的曲线图。下排为不同的耦合项对应于三个相的单粒子能谱图。引自文献[125]。

为了研究Ω = J 的双层系统中拓扑超流体的可行性，他们允许拉曼耦合的相对相位φ 偏离π/2，因此δφ = φ - π/2 ／= 0。在强耦合体系中, 狄拉克点k = 0 处的单粒子能谱中出现了能隙E(δφ) = 2hz=(δφ/2)，相图如图17(a) 所示。在强耦合条件下的相图中可以找到一个拓扑超流相，其特征是陈数C = 1 和配对动量为0。图17(a)、(b) 展示了当化学势进入能隙时，系统发生了从正常超流体到拓扑超流体的相变。此外还通过Q ／= 0 和Q = 0、C = 0 来识别FFLO 态和常规超流态。当Ω = J ＜Erec时，双层系统处于FFLO 态。当耦合强度增加到Jc1≳Erec时，这种FFLO 态将转变到常规超流态。在强耦合条件下，Ω = J ≳1.5Erec，对应于有效Rashba 自旋轨道耦合的极限，当化学势处于能隙(δφ) 范围内时，系统可处于拓扑超流态。因此，在常规超流和拓扑超流之间存在另一个临界耦合强度Jc2。在图17 中，蓝色虚线和红色实线分别表示FFLO 态→常规超流和常规超流→拓扑超流的相变。值得注意的是，由于化学势的增加，常规超流态和拓扑超流态之间转变的临界耦合值会随着结合能的增加而增加。

在二维空间中，正方形晶格中的冷原子可以产生陈数C = 1 的拓扑FF 态[34,130]。如果要实现具有更高陈数的拓扑态，可以借助于复杂的跳跃传导或晶格[131,132]。然而，简单三角形晶格更有利于实现一些拓扑上的非平庸态，它仅仅通过最近邻跳变就可以产生一个陈数更高的拓扑态[133,134]。Guo 等人研究了一个三角晶格上具有自旋轨道耦合和平面塞曼场的系统来实现拓扑FF 态[135]。他们发现具有最邻近跳跃的系统在非相互作用的情况下，能够支持有能隙的陈数C =1 和C = -2 的绝缘体。拓扑相的边界在由面内磁场和面外磁场构成的双参数平面上都是椭圆的。在存在吸引s 波相互作用的情况下，非均匀的FF 超流态可以存在于广泛的区域内。并证明了所有的FF 态在拓扑上都是非平庸的，它们的陈数是C = ±1、±2、±3、±4。他们利用第一布里渊区高对称点的一组Pfaffians(Pfs) 符号来表征不同的拓扑相。随着能隙在相应的点闭合和重新打开，Pfs 的每一个符号都发生了变化。手性边缘态的波函数在开放边界条件下在边界空间局部化，计算手性边缘态可以确定块体是否处于非平庸拓扑态。不同的FF相表现出不同的手性边缘态配对，边界流体直接由边缘模的手性之和的陈数决定。

图18(a)～(d) 总结了量子相。在这里，量子相的特征是超流序参量Δ、质心动量qy、陈数C 和化学势μ。当Δ=0 时，既可以有一个绝缘相(IN)，也可以有一个正常气体相(NG)。对于前一种状态，化学势位于带隙内；然而，对于后一种状态，化学势位于能带中，因此激发态是无能隙的[136]。此外，如果在拓扑上非平庸(这里C =1)，则绝缘相是陈绝缘体(CI)。接下来，具有非零qy的超流体状态(Δ=0) 用FF 表示。FF 态的出现是由于面内磁场hx使费米面[116]变形，标准BCS 超流体(qy=0)只在hx=0 时存在。此外，所有超流相在拓扑上都是非平庸的，并进一步用字母“t”和方括号中的陈数来表示它们。最后，图中的虚线标出了有能隙超流相与无能隙超流相的边界。更具体地说，对于较小的hx，有能隙的超流相的低螺旋度粒子分支能量总是正的。但当hx值增大时，值可能小于零，将会形成无能隙超流体相[117,137]。在图18(a) 和图18(b) 中，分别绘制了参数hx-hz平面上的相图。在图18(a) 中，当hx= 0 时有3 个拓扑相变，这是由粒子空穴对称点处的能隙消失引起的。在面内场的存在下，粒子空穴对称点处的能隙不会同时消失，这是相图如此丰富的主要原因之一。在图18(c) 中表明通过调节化学势可以得到小面积具有陈数C = -3、-4 的FF 相。在图18(d) 中，展示了吸引相互作用的影响，吸引相互作用有利于形成Cooper 对，从而增强FF 相。

V. 拓扑超流的其他现象

A. 孤子引诱的拓扑超流

Liu 等人研究了塞曼场作用下一维自旋轨道耦合原子费米气体简谐势阱中的暗孤子[138–140]。暗孤子的特征是在序参量改变符号并穿过零点时会在点节点处发生180°的相位跳变。由于可以通过改变相位跳变的数目来控制暗孤子的数目，因此可以同时考虑单孤子和多孤子(即孤子序列) 的情况。在拓扑超流相中每个暗孤子都能容纳两个Majorana 费米子，并且在孤子的节点附近具有很好的局域性。可以通过相位印记的控制来创建和移动Majorana 费米子，使其走向现实应用。实验上，可以利用射频光谱的局域态密度或吸收成像的密度分布来探测暗孤子的存在。

值得注意的是，一维的暗孤子与二维的涡旋非常相似。后者也是一种拓扑缺陷，可以在涡核中容纳Majorana 费米子，并在局部态密度和密度分布[141]中表现出来。人们认为拓扑超流中的涡旋晶格是进行拓扑量子信息处理和量子计算的一个很有吸引力的平台[42,142]。此外，有人研究了一维自旋轨道耦合费米气体中单个孤子的性质[143]。这些作者考虑了一组不同的参数，通过增加外部塞曼场，使得部分费米云进入拓扑超流相。

为了在实验上观察暗孤子的点节点上的两个额外的Majorana 费米子，可以使用空间分辨射频光谱学来测量局域态密度。在图19 中，展示了拓扑相变前后的局域态密度ρ(χ,ω)。在BCS 超流体相中，如图19(a)所示，可以很容易地识别出孤子的Andreev 束缚态。在拓扑非平庸相中，如图19(b) 所示，可以清楚地看到两个零能量的Majorana 费米子位于两个势阱边缘。此外，在原点附近存在由两个Majorana 费米子引起的零能量的响应。这个方案与二维拓扑超流体中使用涡旋晶格的想法非常类似，涡旋中心的Majorana 费米子被用作量子单位。在未来的研究中，为了交换不同位置的孤子来证明Majorana 费米子的非阿贝尔统计特性，理解具有复杂序参量和非零速度特征的旅行灰色孤子将是十分重要的[145–147]。

图19. (a) 当h=0.4EF 时BCS 超流的局域态密度和(b) 当h = 0.8EF 时拓扑非平庸超流体的局域态密度。在拓扑相中，暗孤子(χ1 =0) 点节点附近的两个Majorana 费米子，由于波函数的叠加而不可区分。颜色图中以nF/EF 为单位表示局部态密度的大小。引自文献[138]。

B. 三组分的拓扑超流

与凝聚态物质系统中的自旋轨道耦合不同，在凝聚态物质系统中，电子的自旋只有自旋向上和自旋向下两种成分，如40K 和6Li 的冷原子物理中的(赝) 自旋实际上是一个原子的超细态。因此，可以通过具有两个以上超细态的s 波Feshbach 共振制备超流体[148–150]。受此启发，Chen 等人研究了具有三个(赝) 自旋的超流体[151]，并着重讨论了三组分费米气体的拓扑性质。在平均场近似下的一定的参数范围内，三组分费米气体系统可以在更小的磁场条件下实现拓扑超流体。

他们的结果表明，随着塞曼场强度的增大，三组分体系除了经历从BCS 超流体到拓扑超流体的相变外，还可能出现一些其他有趣的拓扑相变。例如，通过适当调整化学势，系统可以在整个塞曼场区域内处于非平庸的拓扑超流体中。还有可能最初是一个拓扑超流体，然后随着磁场的增加转化为一个拓扑上平庸的BCS 超流体。更奇特的是，系统可能会存在重新进入行为[151]，在较大与较小强度的塞曼场上存在拓扑超流体，但在中等强度的塞曼场上存在拓扑平庸的BCS 超流体。因此，系统可以有两个零能量的Majorana 费米子区域。在一定参数范围内，更小的磁场就可以实现这些有趣的拓扑相变，这优化了实现拓扑相的实验。因此，这是一种有希望的实现拓扑相的候选方法。

在图20 中，展示了在给定序参量Δ = Er下三组分超流体(蓝色实线)的相图。为了进行比较，还绘制了双组分超流体的相图(红色虚线)。根据Berry 相的不同行为，可以在μ-h 相图中区分四个不同的相区域，称为I-IV 区域。

区域I(μ ≤μc1=0.53Er)：该区域系统的相变行为与传统的双组分超流体情况非常相似，即存在一个临界塞曼场，系统经历一个拓扑相变，从拓扑平庸相(h ＜hc)到拓扑非平庸相(h ＞hc)。该区域的二组分和三组分体系相边界相交于μ1= -4.59Er和μ2= 0.24Er。结果表明，在μ ＜μ1或μ ＞μ2时，三组分体系拓扑相变的临界磁场小于双组分体系。也就是说，它会变得更容易实现这个有趣的具有更小磁场的拓扑相，这是保持有限能隙超流体的必要条件。

区域II (μ ∈ [μc2,μc3]，μc2= 0.59Er，μc3=3.41Er)：系统在任意h 值处都没有拓扑相变。为了判断该区域的拓扑特征，需要计算Berry 相，即使当磁场h =0 时，该系统也是完全拓扑非平庸的。需要强调的是，区域II 的范围高度依赖于序参量Δ 的值。很容易发现在Δ=0 时, 区域II 的范围是μ ∈(0,4Er)。然而序参量Δ 强度超过临界值会使这个区域迅速缩小。

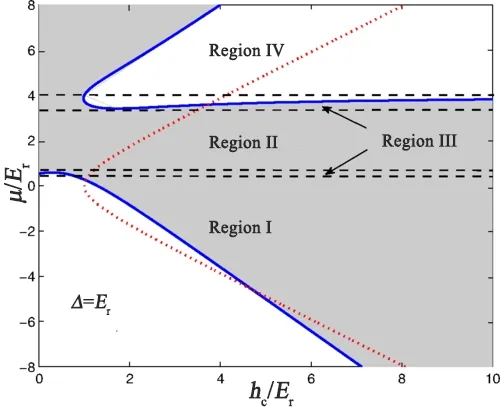
图20. 在Δ = Er 条件下的相图。与双组分超流体(红虚线)相比，三组分情况(蓝线) 更为复杂。四个区域被黑色虚线以不同的化学势μ 划分。灰色区域为拓扑非平庸相。引自文献[151]。

区域III (μ ∈[μc1,μc2]∪[μc3,μc4],μc4=4Er)：在该区域存在hc1、hc2两个临界塞曼场，与区域I 中的传统相变不同，系统首先是拓扑非平庸的，随着塞曼场的增加，它转变到拓扑平庸(h ∈[hc1,hc2])，最后又变成拓扑非平庸(h ＞hc2)。

区域IV (μ ≥μc4= 4Er)：与区域I 相比，它具有相反的拓扑行为; 即系统在小的磁场h 处是拓扑平庸的，而在h ＞hc处则是拓扑非平庸的。对于三组分超流体，即使没有自旋轨道耦合，系统在区域II、III 或IV 上也存在拓扑非平庸相，这与双组分情况有很大不同。原因是对于三组分系统，三个序参量Δ0,-1、Δ1,0、Δ1,-1不会同时满足规范不变性。

C. 大陈数的拓扑超流

大陈数拓扑相[131,152–155]一直是现代物理学中的一个重要课题。Huang 等人研究了耦合层系统中的拓扑超流体[132]，在该系统中，可以通过控制结合能、层间隧穿和层不对称等方式实现不同拓扑超流体之间的相变。这些拓扑相变的特征是能隙在零动量临界点处的闭合和重新打开，陈数和Pfaffian 符号在此处经历一个不连续的变化。边界处受拓扑保护的边模由块体边界对应保证。在势阱中，边模在不同拓扑超流体的界面上具有空间局限性，其中边模的数量等于左右两边超流体的陈数差。由于能带反转和自旋纹理在临界点上离散变化，可以通过零动量或接近零动量的自旋纹理检测到这些拓扑转变。该模型可以推广到陈数等于任意正整数的多层系统。这些大陈数的拓扑超流体为探索超冷原子背景下的奇异量子物质提供了肥沃的土壤。

他们发现在所有的计算中，边模数完全等于陈数C。在图21(a)中，可以发现两种边模在小ky情况下存在速度不同线性色散。图21(c)展示了边模在ky=±0.25kF时对应的波函数，这些位于同一边界的边模沿相同方向传播，见图21(c)内嵌图，这一结果与具有时间反演对称性的固体系统形成了鲜明对比，在固体系统中，位于同一边界的两个边模具有相反的自旋和传播[156–158]。他们还计算了边模的速度作为非对称性的函数。当δμ ＜0.52EF时，其中一种速度相对于δμ 几乎线性增加，而另一种速度单调减小。当2.14EF＞δμ ＞0.52EF时，从C =1 开始，相对速度较大的边模消失，只剩下一个边模。值得注意的是，这个速度的演化是一个跨越拓扑边界的平滑函数，见图21(d)。在平庸相区(δμ ＞2.14EF)，不存在边模。

图21. 在陈数(a) C = 2 和(b) C = 1 的条纹几何中的边缘态。(c)动量ky =±0.25kF 时，各层边缘态的波函数(插图为同一边界动量相同的两种状态的传播方向)。(d) 边缘态速度作为非对称性的函数。(b) 中参数Γ =1.28EF，(a) 和(c) 中Γ = 1.43EF，(a)～(c) 中其他参数εb = 1.2EF 和t = δμ =0.5EF。(d) 在t=0.2EF、εb =0.6EF、Γ =0.97EF 参数条件下，边模的速度作为非对称性的函数。(e) 势阱中广义的块体边界对应。边模空间中定位在两个拓扑超流体之间的接口和边模的数量N =|CL-CR|，其中CL 和CR 是左右界面超流体的陈数, 以及由于手性相反，所有其他的边模都被直接耦合出能隙。一般来说，N =1。引自文献[132]。

Majorana 费米子在ky= 0 时的稳定性对于理解边模的鲁棒性至关重要。同一边的Majorana 费米子具有明确的手性，这种手性阻止了Majorana 费米子的直接融合。然而，在势阱中的情况则完全不同，见图21(e)。由于它们的手性相反，Majorana 费米子可以直接融合，一些边模将会因此消失。剩余的边模数等于界面上左右超流体之间的陈数差。这是势阱中大陈数的拓扑超流体的广义体边对应的体现。在一般情况下，在每个拓扑边界上只能观察到一个手性边模。这些边模可以在实验中单独观测，为测量超流体的局部拓扑不变性提供了重要的依据。

D. 拓扑超流临界温度的提高

2016 年，Wu 等人证明了2D-3D 费米–玻色混合物可以在高临界温度下实现px+ipy拓扑超流体[159,160]。自旋极化费米子被限制在二维平面上，并通过三维玻色–爱因斯坦凝聚体中密度涨落的吸引诱导相互作用进行相互作用。由于诱导相互作用的频率依赖性，二维费米气体的超流相变具有Eliashberg 形式。此外，他们还考虑了迟滞效应，并证明迟滞效应具有重要作用。然后计算了超流体密度，利用BKT 理论确定了转变的临界温度[161–164]。进一步证明了诱导相互作用的强度和范围是可以通过实验控制的。这种可调性可以将超流临界温度提高到BKT 理论所规定的极限值。重要的是，这是在费米–玻色和玻色–玻色相互作用都很弱的情况下实现的，因此三体损失很小。他们的结果为实现高临界温度原子气体中的拓扑超流体提供了一个路线图。

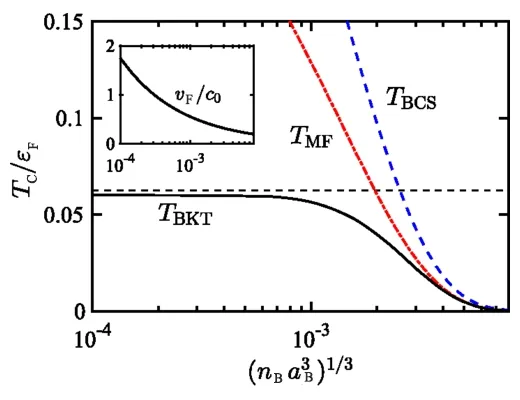
图22. 超流体临界温度在(nBa3eff)1/3 = 0.1 和n1/2F /n1/3B =0.1 的混合物下作为玻色–爱因斯坦凝聚体气体参数(nBa3B)1/3 的函数图，(插入图)νF/c0 随(nBa3B)1/3 变化的函数图。引自文献[159]。

在图 22 中，TMF是40K 和7Li 混合物在和弱费米–玻色相互作用强度条件下的平均场超流转变温度，可以看到转变温度在玻色–爱因斯坦凝聚体气体参数减小时升高。与较小时的费米能量相比，平均场转变温度甚至变得显著，但是很快就会看到相位的涨落大大降低了临界温度。他们还通过忽略迟滞效应，证明了从BCS 理论得到的临界温度TBCS。当νF/c0≪1 时TBCS≃TMF，而当νF/c0较大时，迟滞效应明显抑制了配对。TBKT是BKT 条件下的超流转变温度，当(nBa3B)1/3减小，转变温度迅速达到极限值εF/16。重要的是，这个最大值是在弱费米–玻色耦合时达到的，确保了由于玻色子–费米子二聚体的形成而产生较小三体损失。

他们提出的2D-3D 费米–玻色混合物在实验上是可行的，几个实验小组已经实现了玻色–费米混合，并且可以使用光学势来产生混合维系统[165–167]。此外，临界温度TBKT=εF/16 在实验范围内。他们的建议也适用于二维玻色介质，但在这种情况下，由于二维玻色气体中的强量子涨落，费米子之间的配对预计会更弱。

VI. 拓扑超流的实现与检测

到目前为止，已经有许多关于拓扑超流实现的建议，包括p+ip 超导体[168,169]，三维拓扑绝缘体的表面[88,112]或靠近s 波超导体的一维自旋轨道耦合纳米线[58,170]，以及一维或二维Feshbach 共振附近的自旋轨道耦合原子费米气体[21,36,59]。在与超导电极接触的磁场中[121]，半导体InSb 纳米线隧穿光谱的实验结果已经表明其中可能存在拓扑超流和Majorana 费米子。然而，这些研究仍然缺乏对纳米线的拓扑性质的明确描述。Hu 等人提出了一个由强非磁性或磁性杂质散射诱导的普适中能隙束缚态[36]，它可以为拓扑超流的存在提供明确的信号。在固态中，人们广泛认为杂质是表征其所在系统量子态的重要局部探针。已经可以使用单个杂质来确定非常规非s 波超导的超导配对对称性，并证明了在Be(0001) 表面上[171]的Friedel 振荡。在强相关的多体系统中可以使用杂质来固定一个相互竞争的序参，他们预测了如果一个单一的杂质在拓扑超流中具有足够强的散射强度，就可以创建一个与杂质绑定的普适中能隙态。它类似于涡旋核心内能量最低的Caroli–de Gennes-Martricon(CdGM)束缚态[172]。对于束缚态能量接近于零的序参量，普适束缚态的波函数与Majorana 费米子波函数的对称性密切相关[141]。

根据Anderson 定理[173]，常规的s 波超流几乎不受非磁性杂质的影响。相反，磁杂质可以打破超流的时间反演对称性和粒子间的配对。这导致出现一种与配对能隙内局部杂质有关的中能隙态，即所谓的Yu-Shiba态[174,175]，这种中能隙束缚态的能量由杂质散射势Vimp的强度决定。当Vimp增大时，自旋向上的原子的Yu-Shiba 态从更高的能隙边缘向较低能隙边缘移动，而自旋向下的原子的Yu-Shiba 态则与之相反。研究证明在Rashba 自旋轨道耦合的存在下，如果费米云不是拓扑超流体，即使存在塞曼场，上述说法仍然成立。对于典型的磁场参数h=0.2EF，随着磁性杂质强度的增加，Yu-Shiba 态的位置从一个能隙边缘移动得非常快。相反，一旦塞曼场超过阈值，整个费米云就会变成拓扑超流体，会出现一个完全不同的行为如图23 所示。对于非磁性杂质来说，当杂质强度大于临界强度(Vimp≥0.004r2F)时，一个意外的束缚态将从能隙边缘出现。Vimp增加时，束缚态向零能量方向移动，但永远不会达到零能量。事实上，它的能量很快就饱和到E ≃0.11EF≃Δ20/EF。其中Δ0≃0.307EF是在没有杂质时势阱中心的能隙参数。对于磁性杂质来说，Yu-Shiba 态的位置对杂质强度的依赖性则完全不同。在强杂质散射时，Yu-Shiba 态的能量移动至E ≃Δ20/EF，这几乎与强非磁性杂质诱导的新束缚态具有相同的能量。这种束缚态能量的重合清楚地表明，在拓扑超流中，在强杂质散射的极限下出现了一个普适的束缚态。

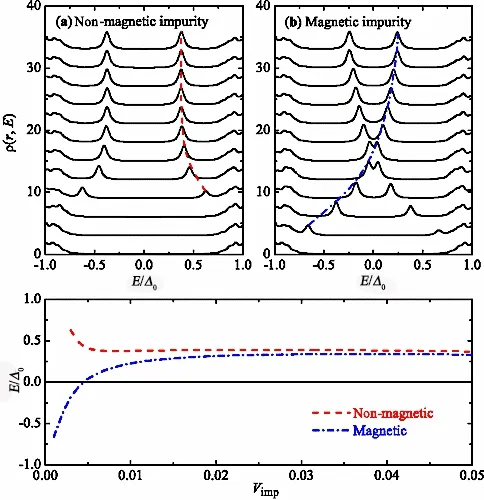
图23. 非磁性三角形杂质(a) 和磁性三角形杂质(b) 诱导的束缚态，V σimp(r)=V σimpδ(r)，在拓扑超流中由总局域态密度的峰值ρ(r,E) 表示。其中ρ(r,E)=Σσρσ(r,E)，ρσ(r,E)=(1/2)Ση[|uση|2δ(E-Eη)+|νση|2δ(E+Eη)]，虚线和虚线突出共振峰的位置是束缚态的能量。从底部到顶部，杂质强度从Vimp =0 至0.011r2FEF，除了Vimp =0 的最低曲线外，其余曲线被清晰度抵消。(c) 束缚态能量与杂化强度的函数，以不含杂质时势阱中心的能隙参数为单位，Δ0 ≃0.307EF。引自文献[36]。

如果杂质散射的宽度有限，杂质诱导束缚态的普适性就会消失。在这种情况下，在强杂质散射极限下会产生一个空穴，而不是点缺陷。因此，存在一系列的边缘态。边缘态的波函数和能量取决于杂质势的形状和强度。在图24 中展示了非磁性(a) 和磁性(b) 高斯杂质诱导的束缚态。很容易看出，随着杂质强度的增加，束缚态永远不会接近普适极限。对于更大的宽度，随着越来越多的束缚态出现，局部态密度会变得非常复杂。

图24. 扩展杂质的普适束缚态的损失。这里取一个高斯散射势，V σimp(r)=[V σimp/(πd2)]exp (-r2/d2)，从底部到顶部，杂质强度从Vimp =0 到0.06r2FEF 增加。引自文献[36]。

这项研究适用于三态超导体Sr2RuO4，对于在InSb纳米线中可能存在的一维拓扑超导，强杂质势会将一维拓扑超导一分为二。因此，在杂质位置预计有两个精确的零能普适束缚态。观察零能Majorana 费米子可以对InSb 纳米线的拓扑性质进行明确的识别。

常见的拓扑性质表现在支撑拓扑缺陷(如涡旋、孤子等) 和无能隙准粒子态。3He 的超流相为研究量子物质的拓扑性质提供了一个通用的平台[176,177]。非平庸拓扑最引人注目的结果之一是涡旋，它在超流体中能够携带半个量子的环流，或在超导体中能携带半个量子的磁通量。人们预测这些涡旋能容纳由核心束缚的非配对Majorana 模[142,178]。因为自旋轨道相互作用使得半量子涡旋不稳定[179,180]，尽管有很好的理论预测，3He-A 中的半量子涡旋在实验中仍然难以观察。同时在d波铜氧化物超导体[181]、手性超导环[182]和玻色凝聚体的晶界上已经观测到了半量子涡旋和磁通量[183,184]。然而，在玻色系统中，涡核束缚的费米子态并不存在，而在超导体中，迄今为止只研究了与涡核无关的半量子通量(在约瑟夫森涡旋或环中)。Volovik 等人研究了在超流3He 极性相中发现的半量子涡旋[38,185,186]。

在μ = π/2 处测量到的信号强度如图25(a) 所示。对于涡旋对的宽度ξD之间的孤子，期望信号为Isat=(nν/2)gsLξD。在这里，L = bn-1/2ν对应于平均孤子长度，其中gs～1 是一个数值因子，它取决于孤子内被困自旋波的分布。数值因子b ～1 与涡旋晶格有关。对于极低涡旋密度和长孤子L →∞，有gs→2。因此，Isat∝Ω1/2，如图25(a) 所示。考虑到拟合参数的缺失和模型的简单性，将实测数据与理论预测的Isat进行比较，表明该模型与理论预测具有良好的一致性。

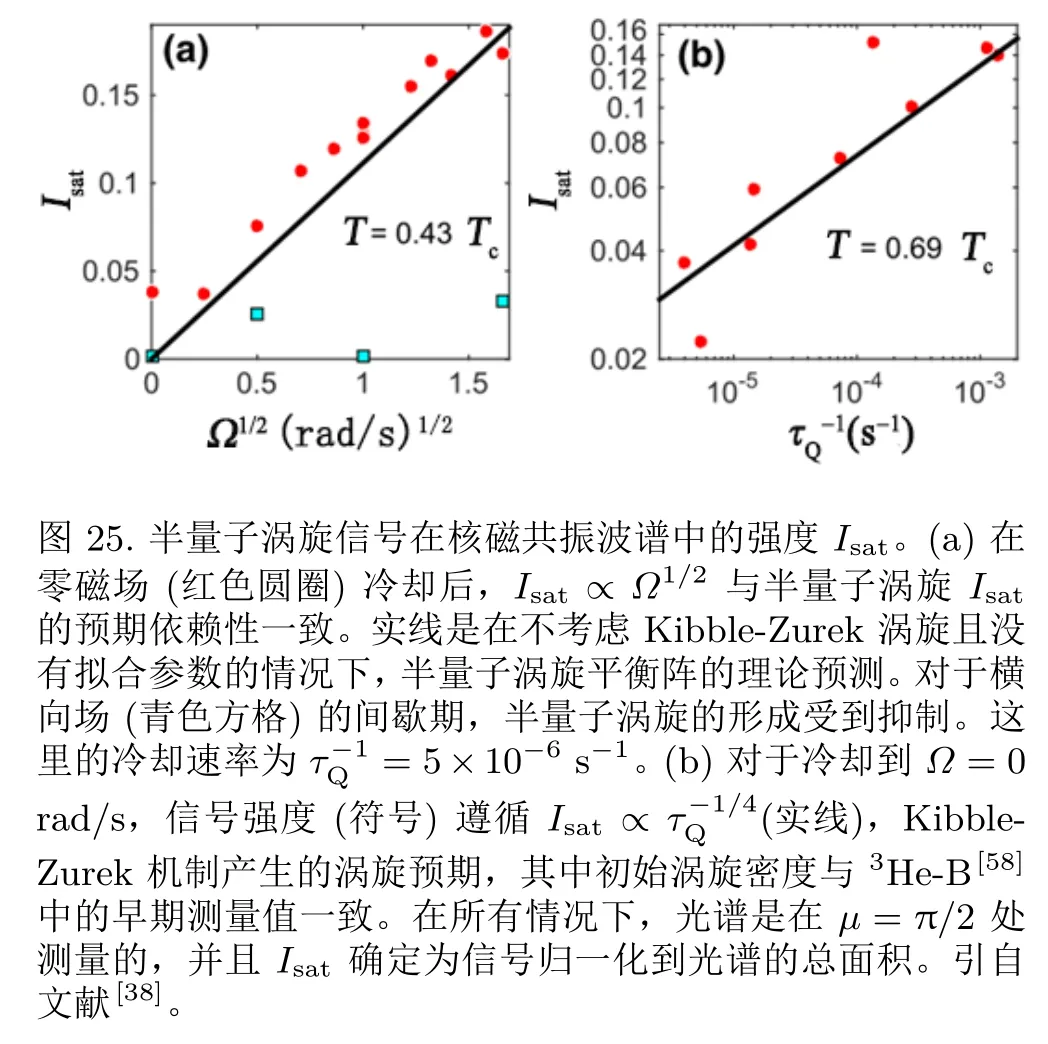
图25(a) 中具有一个显著的特征，在没有旋转的情况下，信号也会出现在零场间歇期。他们将这种现象归因于在二阶相变跨越到极相过程中形成涡旋(缺陷)的Kibble-Zurek(KZ) 机制[187,188]。KZ 机制预计将产生各种序参量缺陷，包括各种可能类型的涡旋。在早期对3He-B 中KZ 机制产生涡旋的观测中，最初形成的涡旋迅速衰减。在Volovik 等人的实验中，最初形成的半量子涡旋由于强烈的钉扎而冻结。涡旋间距离的尺度由KZ 长度lKZ= ξ0(τQ/τ0)1/4确定。对于半量子涡旋来说，涡旋间距离决定了相互连接的孤子的长度，从而决定了信号的幅值。实验中确实观测到的结果依赖于如图25(b) 所示。信号的大小与平均孤子长度1.4lKZ相对应，这也被认为是超流3He 的B 相的初始涡旋间距离[189]。图25(a) 中实验数据高于理论预期的变化表明，KZ 机制在应用旋转的间歇期中也很重要。在未来的研究中，在存在偏置(旋转)和磁通钉扎的情况下，详细分析KZ 机制产生的各种缺陷仍然是一个重要的任务。

Wang 等人提出了一个非常简单的方案[37]，在量子气体中合成p 波超流体[20,21]，不涉及任何自旋轨道耦合或p 轨道原子。其思想的关键成分是一个由两个空间偏移的子晶格组成的自旋相关的光学晶格势，每个子晶格囚禁不同的原子自旋态。这种结构已经在几个冷原子实验室实现了[31,32,95,190]。这种简单的方案诱导了有效p 波相互作用，其强度与本征s 波相互作用强度成正比，本征s 波相互作用强度可以使用s 波Feshbach 共振来调节。他们的建议的简单性使其在实验中更可行，并可能为拓扑超流体及其相关的Majorana 费米子态的研究开辟新的途径。

一维光晶格模型：他们的第一个例子涉及一个简并费米气体，它有两个超精细态(或分别表示为A 和B的赝自旋) 被囚禁在一维光学晶格势中。他们的设置如图26(a) 所示。标记晶格位置使得VB的第j 个位置位于VA的第j 个位置和(j+1) 个位置之间。费米子被深深地困在它们各自的子晶格中，并且在每个子晶格中隧穿是可以忽略的。然而一个子格的Wannier 函数与另一个最近邻子格的Wannier 函数重叠。这为困在两个子晶格中的原子建立了相互作用。可以通过应用射频(rf) 场驱动A 和B 状态之间的转变进一步诱导两个子晶格之间的隧穿。

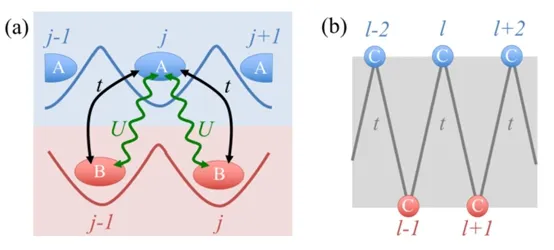
图26. (a) 实验建议的说明: 在一维光学晶格中，超精细态费米子A(蓝色原子云) 和B(红色原子云) 具有相同的晶格势，但相互偏移了半个晶格常数。因此，每个A 原子位于两个相邻B 原子的中心，反之亦然。黑色实线为两个超精细态之间由射频场诱导的耦合。绿色波浪线为原子与原子之间的相互作用，来自不同自旋之间的吸引s 波相互作用。(b) 映射到新的表征表示后的一维无自旋链模型。引自文献[37]。

二维格点模型：他们的第二个例子涉及二维光晶格中自旋为1/2 的费米气体。设置如图27(a) 所示。在这样的二维光学晶格中，每个赝自旋态的费米子都位于四个费米子的中间。再次使用射频场诱导子晶格间的隧穿，而子晶格内的隧穿则被忽略。在前面的例子中，每个原子可以通过两个子晶格势阱VA(r)和VB(r)的Wannier函数的空间重叠与四个最近邻的原子相互作用。为了更清楚地理解系统的拓扑性质，他们将x-y 平面逆时针旋转45°，并通过重新定义费米算符标记将原来自旋1/2的系统映射为具有最近邻p 波相互作用的无自旋费米气体系统，如图27(b) 所示。

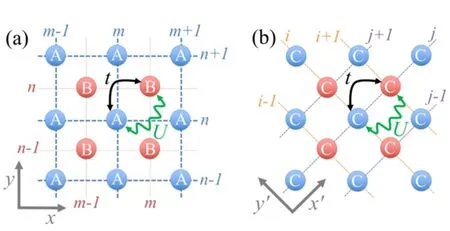
图27. (a) 二维晶格模型说明。一个Asite(蓝色原子云) 被四个Bsite(红色原子云) 包围，反之亦然。与一维模型相似，两个超细态之间的耦合(黑实线) 是由射频场诱导的，原子与原子之间的相互作用(绿波线) 是由不同自旋之间的接触s 波相互作用产生的。(b) 映射到新的索引表示后的二维无自旋晶格模型。引自文献[37]。

利用现有技术，Wang 等人的研究很容易实现。在此，他们对其实施提出了两点构想。最直接的方法是使用驻波激光场，适当调谐其频率，使其在一种自旋态下为蓝色失谐，在另一种自旋态下为红色失谐。这样，两个自旋态的晶格势将相差180°。第二个想法是利用激光场的偏振。例如，在线⊥线构型中，使用两个偏振相互垂直的反向线性极化行波，将形成两个具有σ±偏振和交替最大值和最小值的驻波。这一想法已在一些用来创建自旋相关的晶格势的实验中实现了[191,192]。

Qin 等人研究了杂质与二维p+ip 费米超流体相互作用引起的极化子激发[39,193,194]。他们的结果表明，利用杂质作为探针可以检测背景中的拓扑相变，还揭示了系统中各种多体状态之间有趣的竞争。随着p 波费米–费米相互作用的调谐[97]，超流体在化学势μ ＞0 的弱耦合范围内是拓扑非平庸的。相比之下，在μ ＜0 的强耦合状态下，超流体在拓扑上是平庸的。在μ=0 处发生拓扑相变，此时系统是无能隙的[195,196]。Qin 等人假设一个可调谐的杂质–费米相互作用，并计算了能量、杂质残量和极化子[197–200]态的波函数。当调谐拓扑相变中的背景费米超流体时，极化子能量出现了不连续的二阶导数，这与拓扑相变的顺序一致。另一方面，当调节杂质与费米子的相互作用时，因为杂质残量在有限的相互作用强度范围内迅速减少，极化子态可以渡越到三聚体态。这种极化子到三聚体的转变只在背景费米超流体处于拓扑上平庸的强耦合状态下才会发生。此外，随着杂质–费米子相互作用的增加，极化子态可以变成亚稳态而不是分子态，在分子态中杂质与单个Bogoliubov 准粒子形成局域束缚态。在强耦合状态下，极化子到分子的转变发生在极化子态与三聚体态交渡越之前，因此三聚体态为亚稳态。在弱耦合极限下，极化子态保持基态。通过比较系统中的极化子–分子转变和非相互作用费米海中的杂质–分子转变，研究发现费米超流体背景中的配对相互作用有效地促进了杂质–费米结合。

图28(a) 和28(b) 展示了能量最低的极化子分支，极化子结合能|Ep| 随杂质费米子相互作用强度的增加或费米子相互作用的增加而增加。然后在图28(c) 中展示了Ep对μ 的一阶导数。无论杂质–费米子相互作用如何，在μ = 0 处都会出现转折，这表明了极化子能量二阶导数的不连续性。这与背景中的拓扑相变是一个三阶相变的事实相一致。这样，背景拓扑相变的信息被传递到极化子激发中，由此可以作为相变的探针。在图28(d)中，还展示了杂质残量随Eb变化的函数图。当费米超流体处于拓扑上非平庸的强相互作用态(μ ＜0)时，杂质残量在一个很小的Eb范围内急剧下降，在较大的杂质费米相互作用下，杂质残量基本消失。这是极化子到三聚体渡越的一个明显特征，并且是首次在以s波费米超流体为背景的杂质问题中研究[201]。然而，因为杂质残量的单调减少，但在较大的Eb下仍然是有限的，所以极化子到三聚体的渡越在拓扑上非平庸的弱相互作用区域(μ ＞0) 会变得更加平滑。

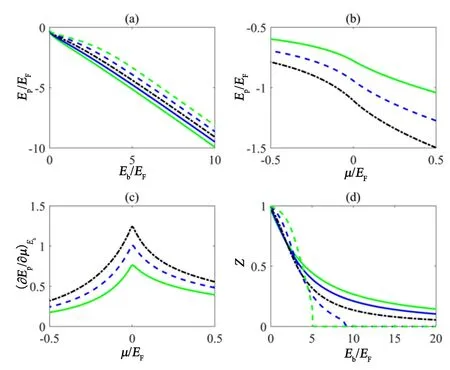
图28. (a) 最低分支极化子能量随Eb 变化的函数。(b) 最低分支极化子能量随μ 变化的函数。(c) 最低支极化子能量对μ 的一阶导数。(d) 杂质残量。参数为Q=0，mb =m，动量截至kc = 20kF。(a) 和(d) 中，绿色实线为μ = 0.5EF，蓝色实线为μ = 0.2EF，黑色虚线为μ = 0，蓝色虚线为μ = -0.2EF，绿色虚线为μ = -0.5EF。在(b) 和(c) 中，绿实线为Eb = 0.5EF，蓝虚线为Eb = 0.75EF，黑虚线为Eb =EF。引自文献[39]。

最近有人提出并通过实验证明了通过圆形二色性[202–204]，即通过分析应用圆形驱动的激发率可以在原子气体中检测到拓扑不变的陈数。这种拓扑探针最初用于非相互作用的陈绝缘体[202]，后来应用于相互作用的多体系统[205,206]。受此启发，Midtgaard 等人通过超流体的圆二色性证明了px+ipy配对的手性[40]。对于弱耦合配对，从相反驱动方向获得的微分激发率由拓扑超流体的陈数决定[202]，这与陈绝缘体十分相似。然而，与陈绝缘体相比，超流体能隙平方的非拓扑贡献对于强耦合配对变得非常重要。利用强耦合Eliasberg 方程结合BKT 理论，可以确定一个较大的和可观测的参数范围，其中具有较高的超流体临界温度，并且二向色信号由拓扑陈数控制。结果表明，二色探针提供了一种很有前景的检测拓扑超流体的实验途径。

玻色–费米混合物的一个吸引人的特征是可以调节二维超流体的临界温度到接近BKT 理论所允许的最大值Tc/TF= 1/16。然而，最大化Tc也将增加能隙，从而增加偏离陈数的微分积分率修正。为了分析这种张力，在图29 中展示了微分积分率ΔΓ 在零温下，当和两种不同的玻色–费米相互作用强度下的临界温度随气体参数变化的函数图。结合Eliashberg 强耦合理论和BKT 理论计算临界温度。发现临界温度随着气体参数的减小而增大，这反映了由玻色–爱因斯坦凝聚体相干长度给出的相互作用范围的增大。因此，能隙也会增加，导致微分积分率偏离ΔΓ = AE2C/2 的修正项更大。但从图29 中可以看出，存在一个明显的区域，在该区域微分积分率均接近拓扑值，且临界温度均接近最大值Tc/TF=1/16。

图29. 在两种不同的玻色–费米相互作用强度下，临界温度(红色) 和微分积分率ΔΓ(黑色) 随BEC 气体参数变化的函数。引自文献[40]。

为了进一步说明最大化临界温度和测量值ΔΓ 的竞争由底层拓扑决定，在图30 中展示了零温下ΔΓ 随Tc的变化函数图。这表明，为了使二向色探针产生接近陈数给定值的值，应该冷却到T ≈0.06EF。由于二维费米气体的温度已经可以降至T ≃0.03EF[207,208]，使Midtgaard 等人的方案在目前的技术范围内有希望检测拓扑超流体。结果还表明，尽管两者的相互作用强度相差不大，但是玻色–费米相互作用强度越强越有利于检测到拓扑超流体。

对于T =0，即使在强耦合中Cooper 对紧密结合，系统处于所谓的BEC 状态[29]，人们也证明BCS 理论是惊人的精确。由此可见，即使在校正项O(Δ2/μ2) 与量化值相差较大的情况下，他们对微分积分率的计算也是可靠的。然而，由于微分积分率在具有时间反演对称性的相中为零，因此任何非零值都表示手性配对。因此，他们的方案还提供了一种方法来观察当μ 在BEC 区域深处变为负时，拓扑相转变到一个平庸相。

VII. 结语

自1970 年人们发现超流体3He-A 相以来，拓扑超流体和超导体的研究一直是凝聚态物理学的一个前沿领域，尽管人们将超导体与拓扑基板混合取得了一些进展，但是在实验上拓扑量子气体还存在着粒子数易损失和寿命短等诸多问题，因此人们对本质上具有拓扑超流性的材料(自然的或人工的) 的探索仍在继续。目前关于拓扑超流的最新研究是在六方氮化硼光学晶格中实现了87Rb 原子的长寿命玻色–爱因斯坦凝聚体并证明了这个手性超流的准粒子激发的能带是拓扑的，且存在边缘激发。寻找新型的晶格材料以及使用新的实验技术是目前探寻拓扑物质的一个主流方向，并且随着人工自旋轨道耦合、塞曼场、光晶格等人工规范场的逐步实现与应用，我们相信在未来会有更多的拓扑材料被专家学者开发出来，应用到更广阔的领域中去。

致 谢

本文得到国家自然科学基金项目(No. 11875149 61565007)、江西省青年井冈学者计划以及江西理工大学清江拔尖人才计划的资助。