含腐蚀缺陷管道失效非线性有限元分析

符方杰

（中国石化天然气分公司河北天然气销售中心，石家庄 050000）

0 引言

油气管道运行过程中，腐蚀会造成壁厚减薄，管道承压能力下降，甚至发生局部破裂，造成油气泄漏。因此，有必要对含缺陷管道的失效压力或剩余强度开展研究。目前，研究的主要方法[1-5]包括实验爆破法、半经验公式法（如ASME B31G、PCORRC等）、数值计算法（如有限元计算）。以文献[6]中9组含长矩形缺陷的全尺寸管道爆破实验数据为基础，开展含腐蚀缺陷管道失效非线性有限元计算分析。对比不同分析位置的选择对管道计算失效压力的影响，并给出最优的失效判定位置点。此外，计算以工程抗拉强度为判定依据下含长矩形缺陷管道的失效压力，并进行修正，用以提高在缺少真实抗拉强度的情况下管道计算失效压力的准确性。

1 有限元模型建立

采用三维20节点实体单元建立管道模型，缺陷类型为长矩形外腐蚀缺陷。为减少计算量，根据对称性，采用1/4管道模型，如图1所示。模型相关尺寸数据[6]如表1所示。模型右端面以及上、下剖面施加对称约束，左端面施加固定约束，内表面施加压力。

图1 含缺陷管道有限元模型

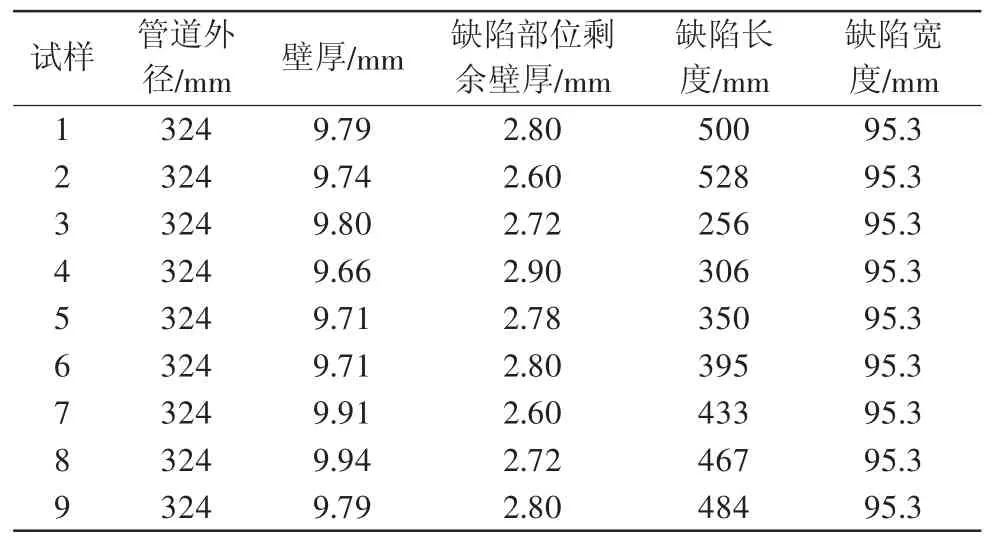
表1 含缺陷管道模型尺寸数据

含缺陷管道在内压作用下的失效过程存在显著的非线性特征。因此，在非线性计算中，管材采用真实应力应变曲线[7]，如图2所示。管道材料为API 5L X60，相应力学性能参数如表2所示，且计算过程考虑大变形问题。失效判据采用塑性失效判定准则[8]：当腐蚀区的应力状态达到材料后屈服终点时，管道发生失效。即腐蚀区域发生失效时，失效起始点在壁厚方向上内、外节点的应力均达到真实抗拉强度。

表2 管材X60力学性能参数

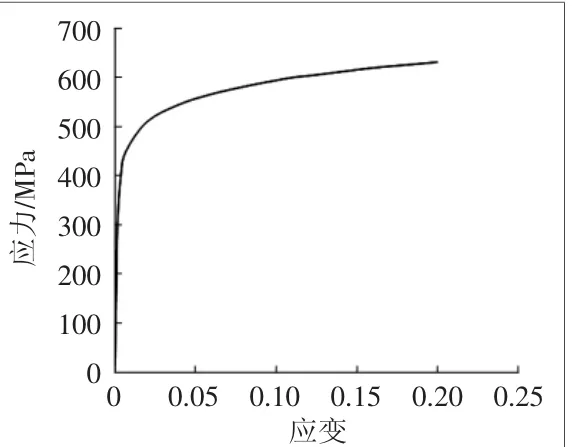
图2 管材X60应力应变曲线

2 有限元计算结果分析

2.1 不同位置点选择对管道计算失效压力的影响分析

长矩形外缺陷管道起始失效点可能位于缺陷的中间或边界处，如图3所示。边界处的应力状态受到倒圆角状态的影响，因此分析中就边界处倒圆角和未倒圆角两种状态分别进行计算分析。边界倒圆角状态下，中间位置为P1，边界位置为P2；边界未倒圆角状态下，中间位置为P3，边界位置为P4。

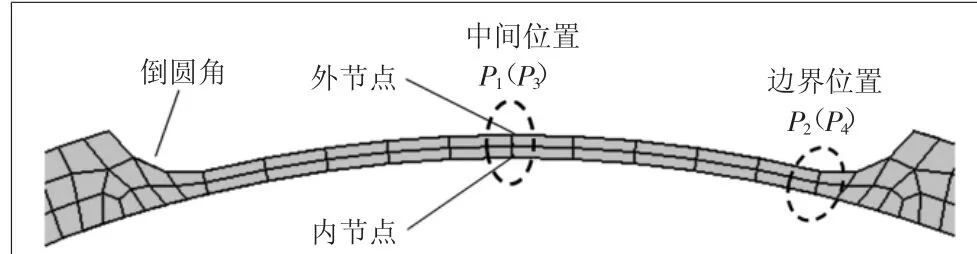
图3 管道腐蚀缺陷圆周截面

计算得到不同内压下P1、P2、P3、P4位置处内、外节点的等效应力。以试样3为例，给出了如图4～图7所示的管道等效应力云图和等效应力-内压曲线。从图中可以看出，中间位置和边界位置的等效应力-内压曲线呈现不同的特征：在中间位置，随着内压的增大，内、外节点之间的等效应力数值相差较小。这是因为缺陷部位剩余壁厚较薄，如表1所示；在边界位置，在曲线的前半部分，内、外节点的等效应力相差比较大，而后半部分内、外节点的等效应力趋于相近。文献[9]～[10]中给出的等效应力状态曲线与图6和图7中边界位置的曲线特征相同，可以看出其采用了边界位置的应力状态作为管道失效判定的依据。

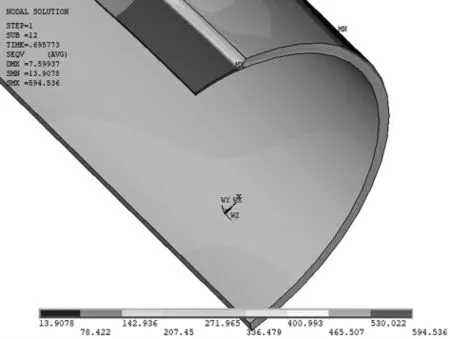
图4 管道等效应力云图（倒圆角）

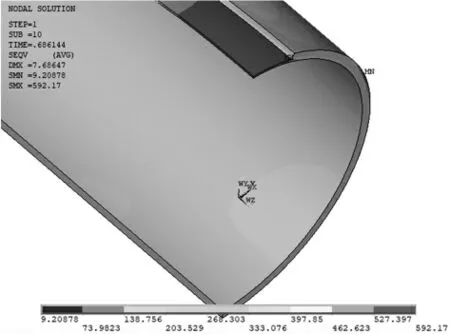
图5 管道等效应力云图（未倒圆角）

图6 管道应力-内压曲线（倒圆角）

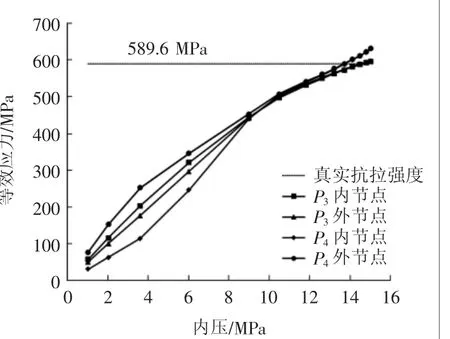
图7 管道应力-内压曲线（未倒圆角）

根据塑性失效判定准则，管道在缺陷的某一位置首先发生失效，则该位置对应的内、外节点的等效应力均应达到真实抗拉强度。以P2位置为例，P2外节点等效应力数值比内节点大，则当P2处内节点的等效应力达到真实抗拉强度时，P2位置处发生失效。此时，P2内节点等效应力-内压曲线与真实抗拉强度线（虚线）相交点对应的内压值即为管道计算失效压力。由此，可得出以P1、P2、P3和P4四个位置处的等效应力来判定管道失效的内压值，如表3和图8所示。

表3 管道失效压力实测值与计算值比较

如图8所示，失效压力点的分布整体上呈现这样的特征：以中间位置计算的管道失效压力的分布更接近于45°等 值 线，而以边界位置计算的管道失效压力偏离45°等值线更远。以P1和P3位置的等效应力为依据计算管道失效压力的值相近。与实测失效压力相比，以中间位置计算失效压力在倒圆角和未倒圆角状态下，最大误差分别为3.6%和3.9%，差异较小。即边界处倒圆角和未倒圆角两种状态，不影响以中间位置的等效应力来判定管道失效压力；以边界位置计算失效压力在倒圆角和未倒圆角状态下，最大误差分别为6.2%和4.7%。因此，可以认为以中间位置的等效应力状态来判定管道的失效压力比边界位置更优。

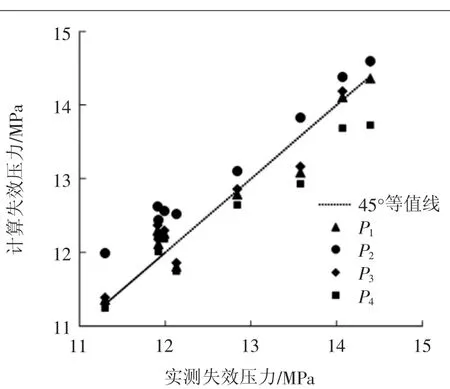
图8 实测失效压力和计算失效压力比较图

从文献[6]给出的管道实物爆破失效形态来看，长矩形缺陷管道爆破位置更多地发生在缺陷的中间位置，验证了上述对比结论，如图10所示。管道试验样管中，缺陷边界处如果不倒圆角或倒圆角较小，则在内压作用下，边界处更容易引起应力集中，管道更容易在此边界处失效。这种情形主要受加工制造因素影响，实际管道腐蚀缺陷中难有发生。在制作含缺陷样管时，应对缺陷边界合理处置，以减少应力集中对结果的影响。

图10 管道爆破失效形态

2.2 以工程抗拉强度判定管道失效压力分析

另外，文献[9]指出，与真实抗拉强度相比，以工程抗拉强度来判定的管道失效压力数值较保守，但未给出具体的保守程度。因此，计算了以工程抗拉强度判定的长矩形缺陷管道失效压力数值，如表4所示。计算的数值取自于P1位置，且边界位置处作了倒圆角处理。从中可以看出，计算的管道失效压力均比实测失效压力小，相差范围为-7.7%～-16.1%。图9给出了以工程抗拉强度判定的管道失效压力y与实测失效压力x之间的拟合关系式：y=x-1.5。在缺少管道材料真实抗拉强度的情况下，可以借助该公式估算管道的失效压力。如表4所示，采用此公式对以工程抗拉强度判定管道的失效压力数值进行修正后，最大误差的绝对值从16.1%降低到5.1%。

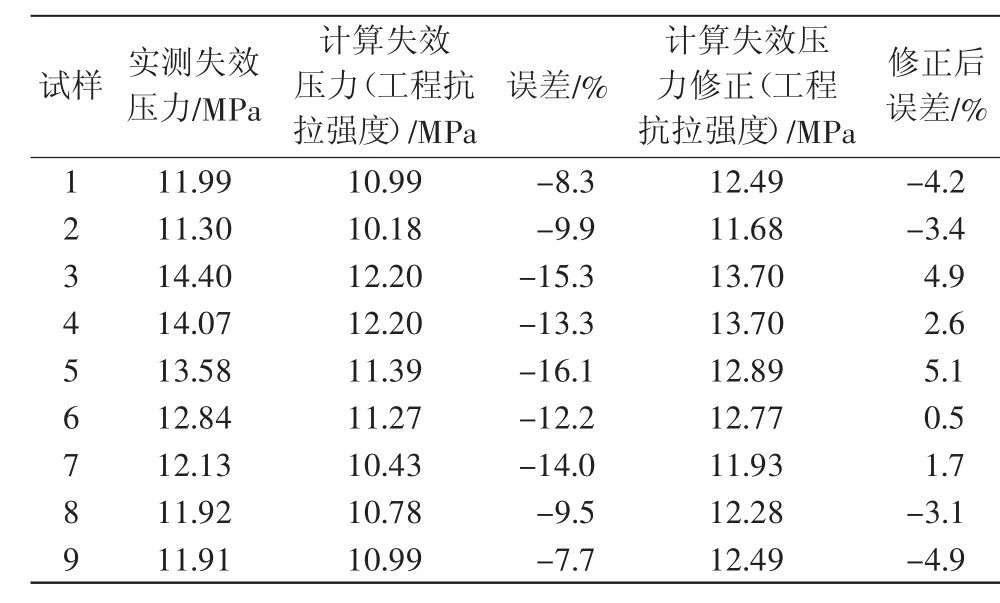
表4 管道失效压力实测值与计算值、修正值比较

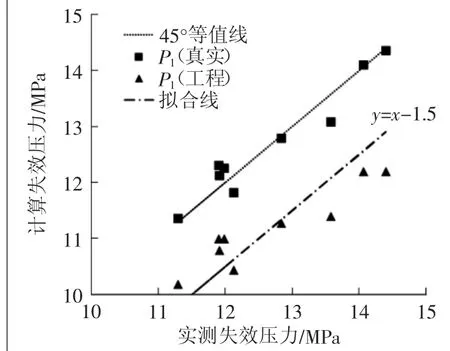
图9 实测失效压力和计算失效压力比较图

3 结语

1）对于含长矩形腐蚀缺陷管道而言，以缺陷中间位置的等效应力来判定管道的失效压力比缺陷边界位置更优，且边界处应作倒圆角处理，其最大误差为3.6%。由管道实物爆破形态可知，长矩形缺陷管道爆破位置更多地发生在缺陷的中间位置，验证了计算结论。

2）给出以工程抗拉强度判定的长矩形缺陷管道失效压力的具体数值，并将计算的管道失效压力y与实测失效压力x进行拟合，得到拟合关系式：y=x-1.5。在缺少真实抗拉强度情况下，该公式可用于修正管道计算失效压力。