面向端对端电能交易的抽水蓄能电站能量交易优化决策模型

刘 淼，张 建，李青春，赵适宜

(辽宁电力交易中心有限公司，辽宁 沈阳 110006)

0 引 言

随着我国经济快速发展和电力消费逐渐增长，具有不确定性和端到端电能交易属性的可再生资源发电模式越来越多的接入到供电网络中[1]，在运行过程中出现的各种不稳定因素使得供电网络越来越需要进行大容量的、可调功耗的供电网能量交易系统[2]。抽水蓄能电站作为供电网中端对端电能交易的直接用户，具有启停灵活性，容量大的特征，在供电网用电量低谷时段即电价低时，购电抽水蓄能；在用电量高峰即电价高的时段，售电放水发电，由此实现供电系统的削峰平谷作用，平衡供电网电力需求，稳定运行。通过输电网实现供电公司与抽水蓄能电站电量的交互，从而获取运营收入。

面向端对端的电能交易需满足用电量、电价、用电用户和可再生资源发电源设置要求[3-4]，可再生资源发电源基于一定的交易机制，在供电方与用电用户中进行选择，以便获取最合适的一方购电或发售电(发电)。我国能源市场逐渐放开，基于用电量需求，有很多学者和专家对抽水蓄能电站优化进行了研究。周攀等[5]构建精细化模型，通过人工群算法求解该模型，得出pareto最佳解集，实现抽水蓄能电站能量交易的优化决策。罗仕华等[6]在市场机制下，通过研究抽水蓄能电站的容量配置优化，实现能量的交易优化决策。高瑾瑾等[7]研究改进序关系分析法，利用三角模糊数系数算法等得出抽水蓄能电站每项指标综合评价值，优化抽水蓄能电站能量交易。以上研究的优化模型，均以消纳风电等多余电量为目标，对供电网调峰的能力不够。

在电能交易中，本文研究端对端电能交易的抽水蓄能电站能量交易优化决策模型，优化抽水蓄能电站出力曲线，以实现抽水蓄能电站收益最大化，保证供电网系统稳定运行。

1 抽水蓄能电站能量交易优化决策模型

1.1 端对端电能交易的抽水蓄能电站工作原理

端对端电能交易的抽水蓄能电站工作逻辑为通过电价高时售电、电价低时用电，从而获得面向端对端电能交易的抽水蓄能电站收益[8-9]。在电力公司电价高时段，将上水库蓄水泄至下水库，进行发电；在电力公司电价低时段，抽水至上水库，完成抽水蓄能电站运行，其电能的双向传输过程通过输电线连接电力公司实现[10-11]。

基于抽水蓄能电站的工作原理，结合电能交易电价，以面向端对端电能交易的抽水蓄能电站收益最大化为目标，构建优化决策模型，既保证供电网在消峰填谷时的电量稳定，又实现面向端对端电能交易的抽水蓄能电站收益最大化。图1为面向端对端电能交易的抽水蓄能电站结构。

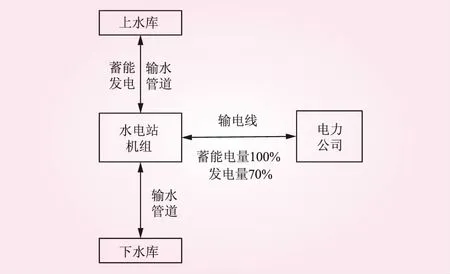
图1 面向端对端电能交易的抽水蓄能电站结构

定速和可变速抽水蓄能机组及三元抽水蓄能机组是面向端对端电能交易的抽水蓄能电站机组的主要机组类型。在以最大功率运行的抽水工况下，定速抽水蓄能机组输出功率不可调节，但是基于定速抽水蓄能机组运行原理，可采用变速泵、液压断流方法调节发电功率，通过停机缓冲实现其发电和抽水工况的相互切换[12]。考虑抽水蓄能机组技术要求和成本要求较高，本文以传统定速抽水机组为研究主体，设发电和抽水的功率为额定功率，研究其通过最大功率发电的抽水蓄能电站能量交易模式。

1.2 电能交易优化决策模型

端对端电能交易条件下，抽水蓄能电站需满足抽水蓄能电站用电量与供电公司电价和供电系统供电量的关系协同设置要求[13-14]，抽水蓄能电站基于一定的电能交易机制，在供电方与用电用户中选择最合适的端对端电能交易条件[15]，供电公司在抽水蓄能电站中，设置并网售电和并网购电2个条件点，当供电系统供电量上升到并网售电条件点时，供电公司满足并网售电的电价条件，即高电价时刻，抽水蓄能电站售电放水发电。当供电系统用电量下降到并网购电点时，满足供电公司并网购电的电压条件，抽水蓄能电站开始购电抽水蓄能。基于上述抽水蓄能电站的工作模式，结合面向端对端电能交易的电价，构建本文面向端对端电能交易的抽水蓄能电站电能交易优化决策模型。该模型以抽水蓄能电站收益最大为优化目标，添加决策变量保证实现工况状态和约束条件间的转换，设置决策变量为每个优化时段抽水、发电时间，参考抽水、发电工况约束和库存容量约束等条件，计算最佳运行时间，得出最佳出力曲线，以此保证供电公司在削峰填谷时供电电量稳定供应。

1.2.1 目标函数

供电收益和抽水用电成本的差值即为抽水蓄能的运行收益，端对端电能交易电价决定其运行收益的高低。分段电价曲线基于预估电价，利用严格单调线性函数拟合度，预估电价，构建目标函数。

设Jn表示优化周期时间，由n个优化时段组成，Ji表示对应各时段结尾时间，严格单调型电价曲线在各优化时间段内用τi(t)描述。分段电价曲线公式为

τi(t)=ait+bi

(1)

式中，ai为电价曲线斜率；bi为电价曲线截距。

选取任意详细优化时间段，若面向端对端电能交易的抽水蓄能电站机组以放水发电运行，一定处于高电价时间段内，若面向端对端电能交易的抽水蓄能电站机组以抽水蓄能运行，一定处于低电价时间段内。通过面向端对端电能交易的抽水蓄能电站机组用最大功率抽水和发电态势，获取最大的发电与抽水工况电价差额。

选取的任意优化时间段的面向端对端电能交易的抽水蓄能电站机组收益公式为

Mi=PgMgi-PpMpi

(2)

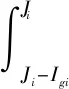
(3)

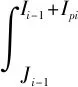
(4)

式中，Mi为第i时段抽水蓄能电站机组的运行总收益；Pg为发电功率；Pp为抽水功率；Mgi、Mpi分别为对应的水库单位容量售电收入、抽水购电成本；ui为单调型电价曲线的二值变量，ui=0、ui=1分别为电价曲线依次减少、增加；Igi为优化时段i的抽水蓄能电站机组发电时间；Ipi为优化时段i的抽水蓄能电站机组抽水时间。

得到完整优化周期Jn的抽水蓄能运行总收入，需求和n个优化时段的收益。本优化决策模型以运行总收入最高为目标函数，其公式为

(5)

目标函数(5)中代入电价曲线公式(1)，整理后得到

(6)

式中，si为第i个优化时段末的电价；s0为初始时间电价。

1.2.2 约束条件

基于面向端对端电能交易的抽水蓄能电站独立运行的特性，达到下述4种约束条件，实现抽水蓄能电站运行抽水蓄能出力的优化调节。发电和抽水功率约束条件为

(7)

(8)

发电功率水流量平衡和抽水功率水流量平衡约束条件为

(9)

(10)

式中，qg、qp分别为发电放水水流量和抽水水流量；c1、c3分别为发电功率、抽水功率函数的二次系数；c2、c4分别为发电功率、抽水功率函数的一次系数。

水库容量约束条件为

Rmin≤R0≤Rmax

(11)

式中，R0为面向端对端电能交易的抽水蓄能电站的水库初始容量；Rmax为最大容量；Rmin为最小容量。

抽水和发电功率互补约束条件为

PgPp=0

(12)

1.2.3 改进免疫粒子群算法

POS算法免疫粒子进化方程为

Vi(t+1)=Vi(t)+c1rand1()(pi(t)-Xi(t))+
c2rand2()(Best(t)-Xi(t))Xi(t+1)
=Xi(t)+Vi(t+1)

(13)

式中，Xi(t)、Vi(t)分别为第i个粒子的位置和速度；pi(t)为粒子i在t时刻的个体最佳值。

代入惯性权重(用ω描述)后速度进化公式为

Vi(t+1)=ωVi(t)+e1rand1()(p1(t)-Xi(t))+
e2rand2()(Best(t)-Xi(t))Xi(t+1)
=Xi(t)+Vi(t+1)

(14)

式中，Besti(t)为t时刻群体最佳解；e1和e2分别为2个学习因子；rand1()和rand2()分别为(0，1)内单独的2个随机数；Xi(t)为第i个粒子的位置；Vi(t)为第i个粒子的速度。

速度惯性对粒子群整体搜索和局部寻优间的协调能力通过惯性权重ω描述，惯性权重值增大表示整体搜索能力强，惯性权重值减小表示局部搜索能力强。惯性权重线性递减方法被应用到很多算法中，惯性权重线性递减方法公式为

(15)

式中，Tmax为重复次数；ωmax为最大惯性权重；ωmin为最小惯性权重；t为目前重复值。

学习因子在异步变化模式里基于对称性原理，可以继续划分为对称性和非对称性，学习因子在同步变化模式中的公式为

e=e1=e2=emax-k×(emax-emin)/kiter

(16)

2个学习因子e1和e2在异步变化中的公式为

e1=e1max-k×(e1max-e1min)/kiter

(17)

e2=e2max-k×(e2max-e2min)/kiter

(18)

式中，k为目前重复次数；kiter为最大重复次数；e1max和e2max分别为两个学习因子e1和e2的最大值；e1min和e2min分别为2个学习e1和e2因子最小值。

分析以上公式可得，粒子仅对局部进行重点查找，说明e1数值较大，换言之，与大部分粒子局部查找能力对应的比重或权重由学习因子e1值体现出来。与大部分粒子全部查找能力上对应的比重或权重由e2值体现出来，粒子会在全局查找，说明e2值较大。最佳解查找时间越短，表明粒子被查找到的时间越短，与粒子查找时间和速度同样重要的是粒子搜索结果的正确率。粒子朝社会群体最佳解BestSi(t)的收敛原则发展，是通过粒子中最佳粒子pi(t)需朝社会最佳群体最佳解BestSi(t)一直学习聚集实现。本文优化决策模型中，在学习进化过程中算法速度和最佳解的收敛搜索准确度同时提高，是学习因子利用非对称线性变化方式优化的结果。

通过改进免疫粒子群算法求解面向端对端电能交易的抽水蓄能电站优化决策模型，计算出抽水蓄能电站的最佳发电和抽水时间和其最佳出力曲线。pBest为同在时刻t的粒子i的个体最佳值向群体最佳解聚集的粒子值。改进免疫粒子群算法求解流程如图2所示。

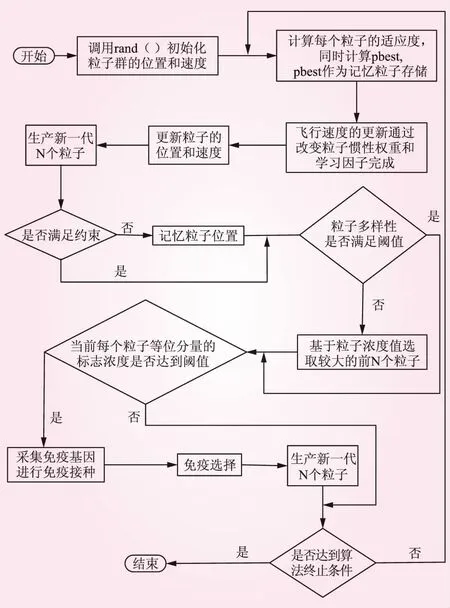
图2 改进免疫粒子群算法流程

2 算例分析

以我国某省端对端电能交易的抽水蓄能电站为研究对象，验证本文模型的能量交易优化决策效果。该省2020年8月26日电价曲线如图3所示。该抽水蓄能电站在当日的额定抽水、发电功率分别为250 MW和230 MW，发电减抽水的循环效率为85%，抽水蓄能的电量上限和下限分别为1 200 MW·h和120 MW·h，库容电量为1200 MW·h，启始库容电量为600 MW·h，最高满水发电时间为4 h。

图3 各时段电价曲线

由图3可知，该市凌晨5∶00和晚上8∶00为2个高电价时间点，凌晨2∶00和22∶00为低电价时间点。

2.1 出力情况对比

选取文献[5]的精细化模型，文献[6]的市场机制模型为本文对比模型，对比分析3种模型优化决策后的抽水蓄能最佳出力情况。

图4为本文模型最佳出力曲线，图5为文献[5]模型最佳出力曲线，图6为文献[6]模型最佳出力曲线。

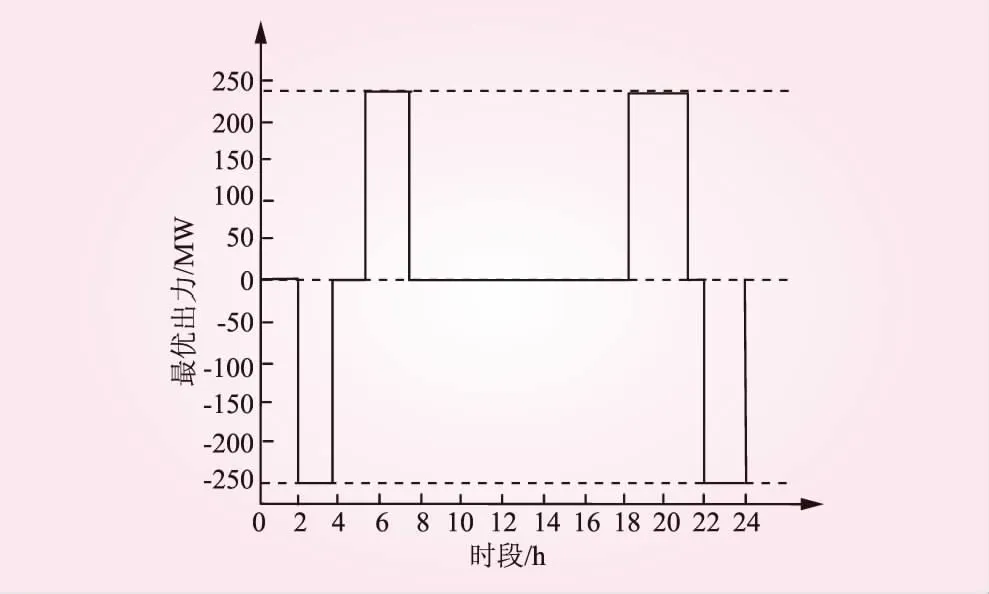
图4 本文模型最佳出力曲线

图5 文献[5]模型最佳出力曲线

图6 文献[6]模型最佳出力曲线

对比图4、5、6所示的3种模型得出的抽水蓄能最佳出力曲线可知，在相同优化时段，对应实验当日电价曲线，负值为抽水出力，正值对应发电出力，3种模型均在当日2次高电价中发电和低电价时抽水，文献[5]、[6]模型抽水时间均未在2个电价最低和最高时间点开始购电抽水和发电售电，且抽水功率和发电功率均低于本文模型，且抽水运行时间长于本文模型。相比2种文献模型，本文模型抽水功率与额定功率相等，且在凌晨2点和晚上22∶00这2个低电价时点开始抽水，抽水时间较短。在凌晨5∶00和晚上8∶00为2个高电价时间点，开始发电售电，发电功率与额定发电功率相等，且发电运行功率稳定。表明本文模型可以准确在电价高或低时发电或购电抽水，且抽水运行时间短，可以实现面向端对端电能交易的抽水蓄能电站收益最大。

2.2 抽水运行成本对比

随着面向端对端电能交易的抽水蓄能电站库存容量和额定功率增加，3种模型抽水运行成本对比如图7。

图7 3种模型的抽水运行成本对比

由图7可知，面向端对端电能交易的抽水蓄能电站在低电价购电抽水时，三种模型抽水蓄能电站能量优化决策后的抽水运行成本均随着抽水容量增加而增长，2种文献模型能量交易优化决策后的抽水运行成本增涨的波动幅度相对本文模型波动幅度较大，且运行成本高于本文模型，本文模型抽水运行成本低且基本呈平稳增涨，说明本文模型优化决策后抽水蓄能电站可以在供电网填谷时保证电量稳定。

2.3 运行收益对比

以该面向端对端电能交易的抽水蓄能电站2020年8月26日运行情况为例，其中，文献[5]模型的经济收益为573 684.7元，文献[6]模型的经济收益为586 389.8元，本文模型的经济收益为667 558.5元，对比3种模型的日运作收益可知，本文模型优化决策后的抽水蓄能电站日运行收益高于文献[5]、文献[6]模型优化决策后的抽水蓄能电站日运行收益，分别高出9.38万元和8.11万元，说明通过本文模型优化后的抽水蓄能电站运行收益较高。

3 结 论

在端对端电能交易中抽水蓄能电站通过低价购电和抽水、高价发电和售电的运行模式，发挥稳定电网运行的作用，并完成自身收入的扩大。本文以最高运行收益为优化目标，构建面向端对端电能交易的抽水蓄能电站能量交易优化决策模型，并利用改进免疫粒子群算法求解决策模型，获取最佳抽水蓄能电站能量交易决策，可获取抽水蓄能最佳出力曲线，达到最低运行成本，运行收益稳定增长，可以实现面向端对端电能交易的抽水蓄能电站运营收入最大化，同时在供电网填谷时保证供电量稳定供应。