不同饱水强度灰岩应变特性及劣化损伤本构模型研究
2022-06-21赵恕轲侯付闯赵明诚杨伟玮
赵恕轲,侯付闯,赵明诚,杨伟玮,
(1.山东省调水工程运行维护中心平度管理站,山东 平度 266700;2. 陕西中凯恒瑞工程项目管理有限公司,陕西 西安 710055;3. 西安科技大学建筑与土木工程学院,陕西 西安 710055)
0 引 言
随着地下工程的快速发展,地下渗透水引发的围岩失稳问题异常突出,特别是我国西南地区,地下水储存丰富且岩溶分布较为普遍。岩溶区具有“高水压、多溶洞”的特点,导致地质构造特别复杂,这给富水岩体工程的安全和高效施工带来困扰。水-岩作用环境下,岩体内部会因水溶蚀作用伴随微裂隙的萌生、扩展、贯通,使岩体力学稳定性被弱化,最终导致围岩体失稳破坏[1-2]。然而,高压渗透水作用又会加剧岩体强度的劣化速度,增加富水隧道的施工风险。因此,探究不同饱水强度下的岩体应力-应变特性和损伤本构模型具有重要意义。
地下岩体赋存于水-岩或水-力耦合环境中,地质构造或外界开挖扰动作用下,经常伴随着应力的重新分配及变形破坏的发生[2-3],因此饱水作用或渗流作用是影响岩体强度和稳定性最活跃的因素之一。为满足实际岩体工程需求,国内外学者开展了水-岩或高水压作用下岩石力学及损伤特性的试验和理论研究。文圣勇等[3]对不同饱水红砂岩进行了单轴压缩试验并分析了水-岩作用下的力学和声发射特征;陈再谦等[4]分析了不同渗透压下灰岩的应力-应变、峰值强度、特征应力、破裂和声发射特性以及劣化机制;康红普等[5]通过水力压裂试验研究了水力裂缝扩展规律;Vasarhely和Van[6]、Yilmaz[7]开展了相关水-岩耦合试验,分析了含水率对岩石峰值强度和弹性模量的影响。傅晏等[8]、姚华彦等[9]、Hale等[10]、Apollaro等[11]开展了涉水边坡岩体在水-岩作用下的物理力学试验。在理论研究方面,众多研究[12-13]将统计理论引入到强度模型中,通过建立岩石损伤与微元体强度间的定量关系,提出了多种模拟岩石变形过程的本构模型。为更好地反映岩石全变形过程的损伤规律,杨明辉等[14]、曹文贵等[15]将Weibull分布模型引入到岩石统计损伤本构模型中,从理论方面揭示了岩石软化过程的损伤演化规律。随着研究深入,基于Weibull分布的岩石统计损伤本构在模拟岩石压缩破坏过程的不适用性逐渐凸显,理论模拟结果与试验压密、弹性阶段的真实变形特性存在一定差异,如何建立考虑压密阶段对岩体应力-应变特性影响的本构模型是解决该问题的关键。
众多学者通过室内试验和理论研究对水-岩作用下岩石力学特性进行了探讨并建立了本构模型,对本文的试验设计与模型建立具有重要指导作用。但目前对于水-岩力学特性的问题研究多是基于不同渗透水压、不同含水率、干湿循环作用下的岩石力学特性展开,对于强制饱水作用下沉积岩的应力-应变特性和本构模型研究较少涉及。为此,本文基于对不同饱水强度处理的灰岩进行的单轴压缩试验,分析了灰岩典型的应力-应变特征,并基于损伤力学理论建立损伤本构模型,研究饱水强度对灰岩的物理力学和损伤特性的影响,可为深部富水岩体工程中的水-岩损伤问题的研究提供参考。
1 灰岩力学试验研究
1.1 试验材料
试验材料采用致密性较好的灰岩,主要矿物成分为碳酸钙、二氧化硅、其他黏土物质,平均含量分别为91%、6.74%和2.26%。岩样取自广西柳州地区,岩性均一,多为次生孔隙,属于低孔隙岩石。干燥状态下灰岩的电镜扫描图像见图1。

图1 灰岩电镜扫描图像
为满足试验需求,根据国际岩石力学测试标准,通过现场取样、切割、打磨后,制作成直径50 mm、高100 mm的圆柱体岩样,端面不平行度小于0.02 mm。试验考虑了0、3、6 MPa和9 MPa等4种强制饱水状态,共制作了12个岩样。由于饱水强度为手动操作,4种实际饱水强度分别为0、2.98、6.04 MPa和9.08 MPa。为保证灰岩材料具有相同的初始含水率,试验前对所有岩样常温下风干24 h。然后,测试试验灰岩物理力学参数,见表1。
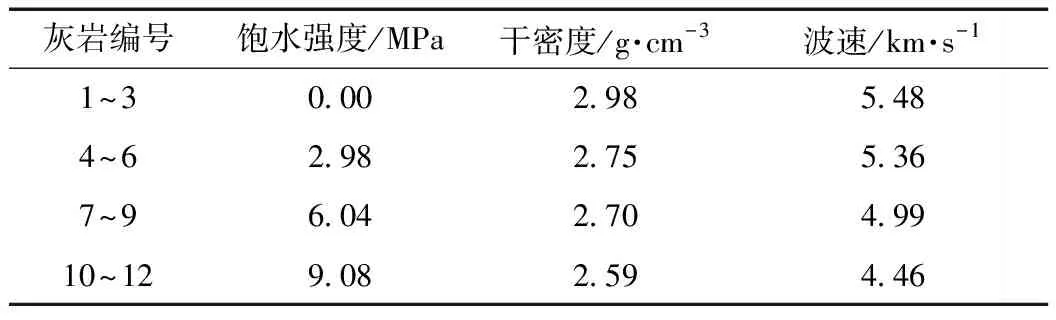
表1 灰岩物理力学参数
1.2 试验设备及方法
采用RMT-150C岩石力学试验系统对不同饱水强度下的4组灰岩进行单轴压缩试验。试验设备包括力学试验机、强制饱水设备。力学试验机的最大试验力为600 kN,可实现不同加载速率下的轴向加载试验;强制饱水设备可对灰岩进行不同强度的饱水试验,以模拟不同富水环境下岩体的饱水状态。
试验方法:①将风干24 h的灰岩试样分别置于饱水设备中,不同饱水强度下强制饱水12 h,取出后用保鲜膜包裹密封以防止水分散失。②将饱水灰岩试样两端磨平,利用毛刷清除两端面杂物,涂抹耦合剂,然后安装于力学试验机上。③在试样表面安装应变计,以测试加载过程中的应力-应变曲线。调整好试样使其处于加载轴线上,为获得稳定的应力-应变曲线,力学试验机的应力加载速率为0.25 MPa/s,直到灰岩破坏。
2 试验结果分析
将试验数据进行处理,得到不同饱水强度下灰岩的应力-应变曲线。灰岩的典型应力-应变曲线见图2。从图2可知,不同饱水强度下的灰岩试样应力-应变曲线发展趋势基本相似,总体均经历了压缩密实阶段(OA阶段)、弹性变形阶段(AB阶段)、裂隙萌生与扩展阶段(BC阶段)和破坏变形阶段(CD阶段)。由于强制饱水作用,灰岩强度被显著弱化,峰值强度随饱水强度增加而逐渐减小。以9.08 MPa的应力-应变曲线为分析对象,灰岩的阶段应力-应变特性如下:
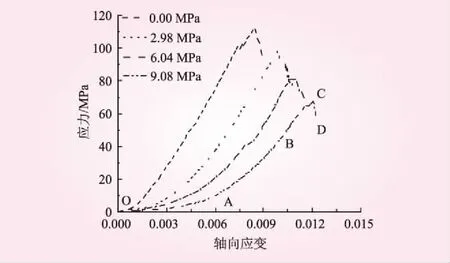
图2 灰岩的典型应力-应变曲线
(1)压缩密实阶段(OA阶段)。随着轴向应力加载,灰岩内部原生孔隙以及部分新生裂隙逐渐被压缩至密实,应力-应变曲线表现为缓慢上升。由于灰岩平均干密度为2.68~2.75 g/cm3,故孔隙度相对较小。对于0 MPa的灰岩,其内部孔裂隙很快被压密,导致压缩密实阶段相对较短。随着饱水强度的增加,水-岩作用引起内部孔隙数量及尺寸逐渐增大、矿物成分散失,软化效应使得压缩密实阶段相对延长,灰岩进入弹性变形阶段的应变值逐渐滞后。这表明饱水强度对应力-应变曲线的压缩密实阶段具有显著影响,饱水强度越大,灰岩的压密阶段下凹越明显,应变路径越长。
(2)弹性变形阶段(AB阶段)。随着轴向应变逐渐增大,内部孔裂隙进一步被压缩,灰岩的应力-应变曲线开始呈线性增长,随着饱水强度的增加,应力-应变曲线的线性增长减缓,弹性模量减小。此外,相比较小饱水强度下的弹性变形,饱水强度越大,其弹性变形路径相对缩短。这是由于经过不同强度的饱水处理后,灰岩内部裂隙水压加剧了矿物剥离速率,孔隙度增大,不稳定裂隙的扩展规模显著提高,进而导致灰岩的应变能提前释放[3]。
(3)裂隙萌生与扩展阶段(BC阶段)。相比弹性变形阶段,该阶段的应力-应变曲线表现出上凸特点,且饱水强度越大,应力-应变曲线上凸越明显。这是由于随着饱水强度的增加,孔隙水压加剧了灰岩的劣化,新生裂隙与原生孔隙贯通形成了破坏裂纹,岩石结构逐渐发生塑性变形。随着轴向应变的发生,灰岩逐渐屈服达到破坏强度。饱水强度越大,灰岩峰值强度越小,相比干燥灰岩,饱水强度为2.98、6.04 MPa和9.08 MPa下的峰值强度分别降低了12.95%、27.56%和38.75%。灰岩峰值强度σc与饱水强度n呈线性关系,即
σc=-4.86n+112.14
(1)
(4)破坏变形阶段(CD阶段)。随着应变增大,灰岩内部的大量微裂隙快速交汇贯穿,逐渐形成微裂缝。而随着轴向荷载的增加,灰岩裂缝快速贯穿形成可见裂纹(见图3),主裂纹的出现预示着试样破坏(由于应变计链条的遮挡,部分贯穿裂纹未完全显示)。
对于0 MPa的灰岩,靠近试样下端面处多处岩块飞出,试样表面呈多处岩块缺失区;而较大饱水强度下的灰岩试样较少或未出现此现象,这表明饱水强度弱化了灰岩的脆性破坏特性。试验表明,灰岩试样破坏形式包括剪切破坏和鼓状破坏,剪切破坏占总试样的91.67%,说明饱水强度对灰岩的破坏类型未造成较大影响。
3 不同饱水强度下灰岩劣化损伤特性
3.1 劣化损伤本构方程
Lemaitre应变等效假说[12-13]认为,岩石材料在变形前后应变等价。基于此,建立岩石损伤本构关系为
σ=Eε(1-D)
(2)
式中,σ为有效应力;E为弹性模量;ε为应变;D为损伤变量。
假设岩石为各向同性材料,微元体强度参数F满足Weibull分布,则岩石材料微元体强度的概率密度函数为
(3)
式中,m和F0为Weibull分布参数。
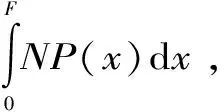
(4)
由式(3)和(4)可知,岩石损伤变量D为微元体强度参数F的函数。对于单个微元体的破坏准则,将式(3)代入式(4)可得Weibull分布的损伤变量D为
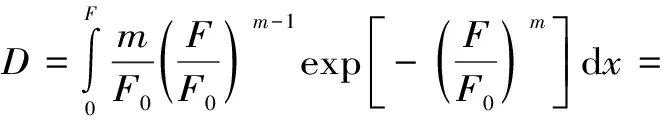
(5)
由式(5)可以看出,岩石损伤本构模型的建立与Weibull分布参数m、F0以及微元强度参数F有关。
3.2 微元强度参数以及损伤本构方程
Drucker-Peager破坏准则具有参数形式简单、广泛适用于岩石介质等特点[16]。选择Drucker-Peager破坏准则作为判断微元体破坏的判断准则,则有
(6)
式中,φ为岩石内摩擦角;I1为应力张量的第1不变量;I2为应力张量的第2不变量。I1、I2分别表示为
(7)
(8)
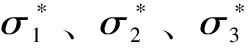
(9)
式中,E、ν分别为岩石弹性模量、泊松比;ε1为应变;σ3为围压。
2009年版和2017年版《国家基本医疗保险、工伤保险和生育保险药品目录》对比及发展研究 ……………… 沈怡雯等(9):1153
将式(9)代入式(5)后,可得灰岩损伤变量方程

(10)
将式(10)代入式(2),灰岩损伤本构方程为
(11)
3.3 损伤本构方程的求解与验证
3.3.1 损伤本构方程的求解
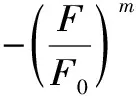
(12)
对式(12)两边取对数,可得
ln[lnEε1-ln(Eε1-σ1+2νσ3)]=mlnF-mlnF0
(13)
式(13)表明,本构方程依然包含众多未知参数。为获得损伤本构方程的理论解,参考文献[12]中的研究方法对其进行求解。
假定y=ln[lnEε1-ln(Eε1-σ1+2vσ3)],x=lnF,n=mlnF0,将假定函数y,x,n代入式(13)可得
y=mx-n
(14)
式(14)表明,y为x的一次线性函数,m,n值为与饱水强度相关的参数变量。假设灰岩应力-应变曲线的压缩密实阶段与弹性阶段的分界应力为σd,则应力-应变曲线的σ<σd阶段和σ≥σd阶段对应的表达式为
(15)
通过式(15)分别对应力-应变曲线进行数值拟合,即可得到与饱水强度相关的参数变量m,n值。再将m,n值代入,即可求得宏观强度参数F01、F02
(16)
3.3.2 损伤本构模型验证
基于上述分析,利用式(15)分别对应力-应变曲线分段拟合,可得到m,n值;利用式(16)求得参数F01和F02,结果见表2。基于试验测试,E、ν的平均值分别为18.96 GPa和0.32。
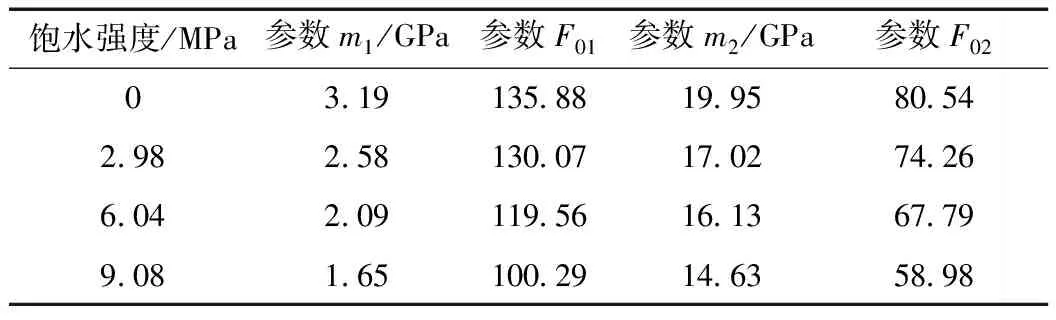
表2 参数m1、m2、F01、F02值
从表2可知,随着饱水强度的增加,σ<σd阶段和σ≥σd阶段的参数m1和m2均逐渐降低。相比饱水强度为0 MPa时,2.98、6.04、9.08 MPa条件下的m1分别降低了19.12%、34.45%和48.28%,m2分别降低了14.69%、19.15%和26.67%。随着饱水强度的增加,参数F01、F02值也呈逐渐减小趋势,这是由于参数F0反映了岩石的宏观平均强度[17],这与式(1)和图2中分析结论一致。
灰岩应力-应变曲线的σ<σd和σ≥σd阶段的参数m1、m2、F01、F02随饱水强度P0的变化趋势以及数值关系见图4。从图4可知,函数参数m1、m2、F01、F02随饱水强度的增加呈二次或三次函数变化。这是由于饱水强度增大了灰岩含水率,加剧了灰岩成孔速度,导致脆性降低和强度弱化,张二峰等[18]
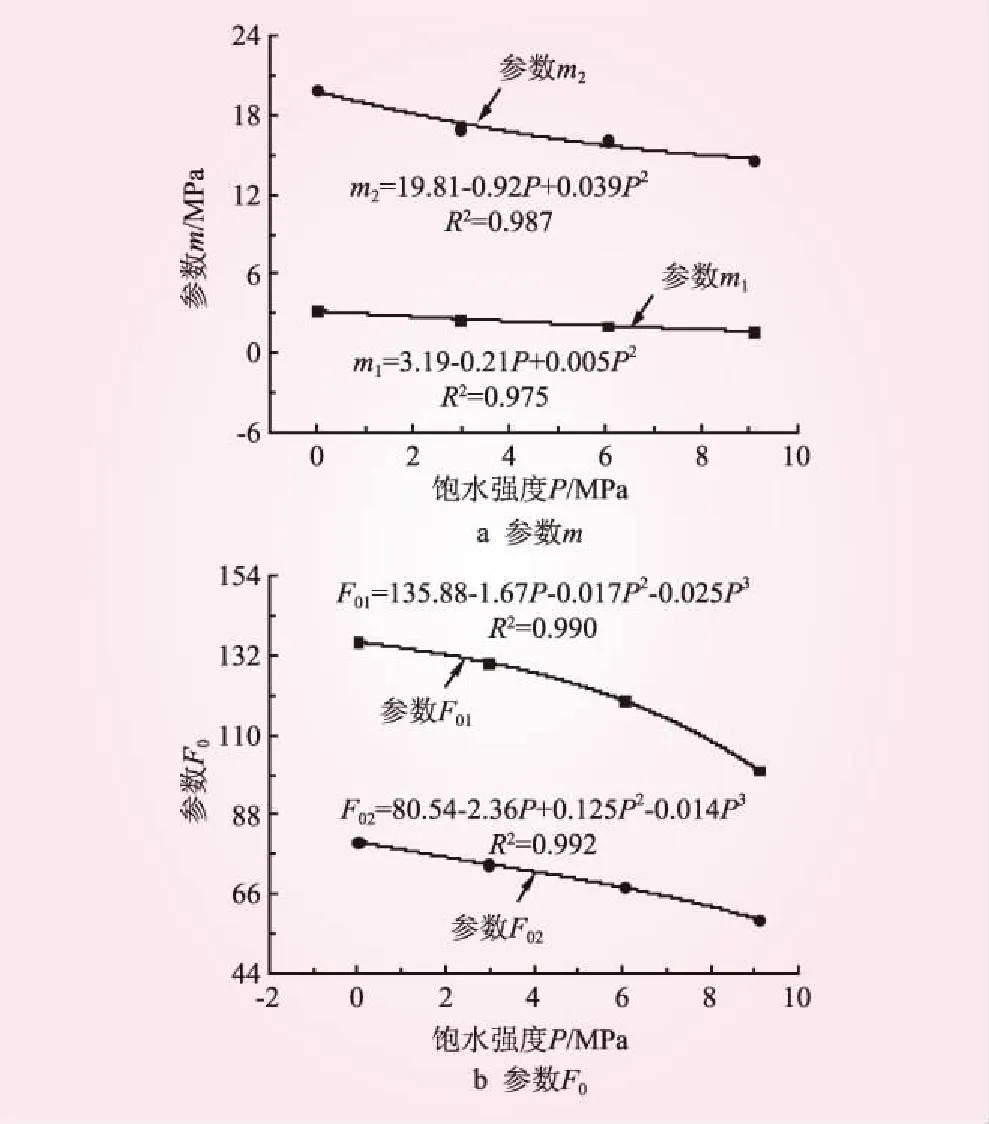
图4 模型参数m和F0的变化趋势
也得到过类似结论。结合式(14)和表2中m1和m2可以发现,m1、m2值与应力-应变曲线的瞬态弹性模量具有相同的物理意义。这是由于随着灰岩饱水强度的增加,岩石内部溶蚀孔隙的数量、尺寸逐渐增加,强度劣化也逐渐明显。随着m的降低(饱水强度增加),岩石软化越明显。因此,参数m可反映岩石脆性特征以及内部微元强度分布特性,这与何志磊等[19]研究结果具有一致性。
结合式(9)、式(12)及表2可得到不同饱水强度下的灰岩损伤本构关系,不同饱水强度下灰岩应力-应变曲线与模型曲线见图5。图5中从左至右4组曲线的实线和虚线分别为0、2.98、6.04、9.08 MPa试验值与模拟值。从图5可以看出,不同饱水强度下应力-应变曲线与模型曲线的发展趋势基本相似,表明所建立的损伤本构模型较好模拟了灰岩的应力-应变特性。饱水强度为0 MPa时,应力-应变曲线与模型曲线重合度较高,这是由于无饱水对灰岩的物理力学特性影响较小,本构模型能够很好反映灰岩的应变规律。随着饱水强度的增加,灰岩应力-应变曲线与模型曲线出现较大的偏差,这主要与灰岩内部新生孔隙的分布状态以及采用分段拟合求解本构参数所产生的误差有关。由于建立本构模型时充分考虑了压缩密实阶段对灰岩应力-应变特性的影响,应力-应变曲线的σ<σd阶段试验值与模型值具有很好的一致性。
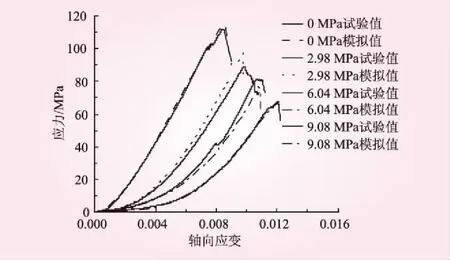
图5 灰岩应力-应变曲线与模型曲线对比
4 结 语
本文对不同饱水强度的灰岩进行单轴压缩试验,研究饱水强度对灰岩力学特性的影响。基于试验结果分析了典型应力-应变曲线特征,并根据损伤力学理论建立了损伤本构模型。得出以下结论:
(1)灰岩应力-应变曲线经历了压密阶段、弹性变形阶段、裂隙萌生与扩展阶段及破坏变形阶段;相比低强度饱水灰岩,高强度饱水灰岩的压密阶段相对延长,弹性变形阶段相对缩短。饱水强度加剧了灰岩软化效应,灰岩峰值强度呈线性函数衰减。
(2)饱水作用弱化了灰岩的脆性特征而未对破坏类型造成较大影响。灰岩的破坏类型包括剪切破坏和鼓状破坏,剪切破坏为灰岩的主要破裂形式。
(3)随着饱水强度的增加,模型参数m和F0分别呈二次和三次函数降低。模型参数m和F0对揭示灰岩的脆性和强度特征具有重要意义。
(4)对比不同饱水强度下灰岩的应力-应变曲线与模型曲线表明,模型曲线和试验曲线的吻合度较高,表明建立的损伤本构模型具有可靠性。
