基于侧压力系数变异性的隧洞围岩变形响应特征研究

刘学军，刘晓东，谢良甫，3

(1.新疆建筑科学研究院(有限责任公司)，新疆 乌鲁木齐 830002；2.新疆大学建筑工程学院，新疆 乌鲁木齐 830046；3.新疆土木工程技术研究中心，新疆 乌鲁木齐 830046)

0 引 言

近年来，国家不断加大对西部地区的开发力度，川藏及秦岭公路隧道、精河-伊宁铁路、南水北调西线、二郎山公路隧道、乌鞘岭隧道等[1-2]深埋长大隧道工程逐渐增多。隧道在开挖过程中，破坏了围岩应力平衡状态，使岩体发生变形破坏，危及工程施工及作业人员生命财产安全，此类问题在高地应力地区深埋隧道的建设中显得更加突出。深埋隧道的稳定性受到围岩等级、地层构造、地下水、开挖方式、支护类型及时间等众多因素影响，一旦发生不合理的变形，将造成不可挽回的重大损失。此外，高地应力地区岩体在其自重体积力存在的条件下，由地质构造运动产生的水平应力场也会对工程建设产生巨大影响[3]。

国内外众多学者对开挖过程中隧道在不同应力水平下产生的变形规律开展了多方面的研究，通过将现场实测数据与经验结合的经验公式法[4-5]、数值模拟法[6-7]和模型试验法，总结分析了多种条件下的隧道变形规律，为解决隧道开挖过程中的沉降变形问题及变形预警预测提供了可贵的依据。方超等[2]利用三维有限元数值模拟软件ABAQUS，研究了在不同侧压力系数下围岩的变形规律和支护措施的力学响应规律；余莉等[8]进行的高地应力地区隧道围岩分级研究，指出了在高地应力隧道中侧压力系数对隧道稳定性的重要影响；李占海等[9]利用数值模拟软件，通过研究不同侧压力系数下隧道的损伤机制及围岩变化情况发现，侧压力系数对隧道的损伤机制有着重要影响；赵德安等[10]研究了不同侧压力系数下隧道变形规律及衬砌结构的力学行为。

众多学者开展的不同侧压力系数对隧道工程影响的研究，为隧道工程的安全施工提供了宝贵的经验。但是，在利用数值模拟软件进行深埋隧道的模拟时，较少有学者提及初始应力场的响应问题，而初始地应力场选取的正确与否将直接影响数值模拟结果的准确性。为此，本文基于李仲奎[11]提出的适用于深埋隧道数值模拟初始地应力场生成的方法，结合三维有限差分数值模拟软件FLAC3D，以在建的东天山隧道工程为依托，生成符合实际情况的初始地应力场，分析不同侧压力系数对隧道不同部位变形规律的影响，为后续施工段工程开挖支护提供依据。

1 工程概况

G575线巴里坤—哈密是新疆维吾尔自治区“57712”交通规划“五横七纵”高速、高等级公路网中“第五纵”老爷庙—巴里坤—哈密—若羌的重要组成部分，也是《国家公路网(2013年～2030年)》新疆境内新增的9条国道之一。东天山隧道是本项目的重点工程，隧道左线起讫桩号 ZK8+809.00～ZK20+576.00，右线起讫桩号K8+783.00～K20+558.00，左右线平均长11 771 m。隧道区总体属于高中山地貌，局部分布丘陵地貌及山间沟谷地貌，地势较高且起伏较大，隧道范围内高程2 040～3 375 m，最大相对高差约为1 330 m。围岩以Ⅲ～Ⅴ级为主，地层岩性主要以凝灰质砂岩、凝灰岩、花岗岩等硬质岩为主。隧道通过地段穿越4条断裂带，地质构造活动较强。所在地区属大陆性干旱气候，气温差异明显，季节性降雨与山区融雪易产生破坏性较强的洪水。总之，隧道整体区域地形、地质、水文、气象等条件均较为复杂。

垂直洞轴线方向的最大初始应力σmax与岩石饱和单轴抗压强度Rc的比值被称作围岩强度比Gn，是判定围岩稳定性的重要指标，也作为是否产生高地应力的判定标准[12]。监测数据显示，东天山隧道工程区Gn在2.1～6.5区间内，侧压力系数λ在0.8～1.6区间内，表明隧道属于高地应力区，且隧道内基本由水平应力占主导作用。由于该隧道侧压力系数变化范围较大，构造应力场多样，为保证后续施工的正常开展，研究不同侧压力系数对隧道变形规律的影响是十分有必要的。

2 模型建立

2.1 网格划分

选取隧道右线K9+150-K9+180段做模拟段，围岩以凝灰质砂岩为主，分布厚度较大。隧道采用台阶法开挖，采用复合式衬砌结构。利用有限差分软件FLAC3D模拟实际工况。原有的经验值6倍半径适用于一般隧道，但因该隧道埋深较大，在确定隧道围岩影响范围时，为提高结果的准确性，选取10倍半径。此外，为更准确分析变形规律，在6倍半径以内对模型网格单元进行加密处理。6～10倍半径内，为简化计算，将模型网格单元在合理范围内进行放大。最终，建立模型尺寸为120 m(x向)×30 m(y向)×95 m(z向)。整体模型单元总数62 000个，节点总数60 078个。隧道模型见图1。

图1 隧道模型网格

2.2 模型实现

模型采用摩尔-库伦(M-C)本构模型，支护结构按照实际施工情况进行，初期衬砌采用喷射混凝土+钢支撑的综合防护系统，二次衬砌采用整体模筑混凝土进行，模型开挖过程通过将开挖部分赋予Null-Model空模型实现，当材料被赋予Null-Model空模型即代表材料被挖除，衬砌部分通过将Null-Model模型重新赋予弹性本构模型并添加相应的参数来实现。

在模拟中，首先要进行初始地应力场响应检测。若响应良好，即模拟生成的初始地应力场与实际地应力场基本吻合，则进行第1施工段的开挖和初次衬砌工作，第1施工段的二次衬砌将在第2施工段初次衬砌完成后进行，循环开挖直至整个过程结束。模型围岩和衬砌系统计算参数参照勘察报告选取，具体数值见表1、2。

表1 围岩参数

表2 衬砌参数

2.3 监测点布置

为更好监测开挖过程中的隧道变形，分别在指定断面拱顶、拱脚、拱底以及距拱顶3R(3倍隧道半径)、6R(6倍隧道半径)和模型顶部(60 m)设置监测点，以获取隧道不同部位及埋深的变形，见图2。竖向监测点顺序依次为1～6，并在隧道顶部沿水平方向(x方向)均匀布置监测点，以监测开挖进程中距隧道轴线不同距离的拱顶沉降变形，获取沉降槽曲线。

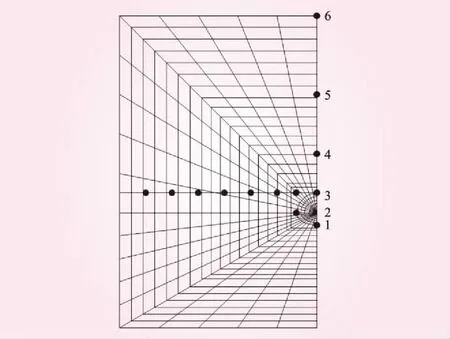
图2 监测点布置

3 初始地应力场响应

3.1 快速应力边界法(S-B法)

FLAC3D软件利用常规方法生成的初始地应力场中，通过对模型施加速度边界条件来实现位移边界约束条件。这种方式生成的初始地应力场一般均为自重应力下的应力场，在浅埋工程中能够与实际地应力场较好的吻合。但在深埋工程中，由于较大的构造应力使常规方法生成的初始地应力场难以满足实际地应力场。国内外众多学者对复杂地质条件下初始地应力场的生成展开了大量的研究[13-16]，提出了多种不同条件下的初始地应力场的生成方法。

快速应力边界法是一种生成深埋工程初始地应力场的方法，见图3。该方法通过在模型边界直接施加应力的方式形成应力边界条件，使模型在初始地应力平衡后得到与实际相吻合的地应力场。

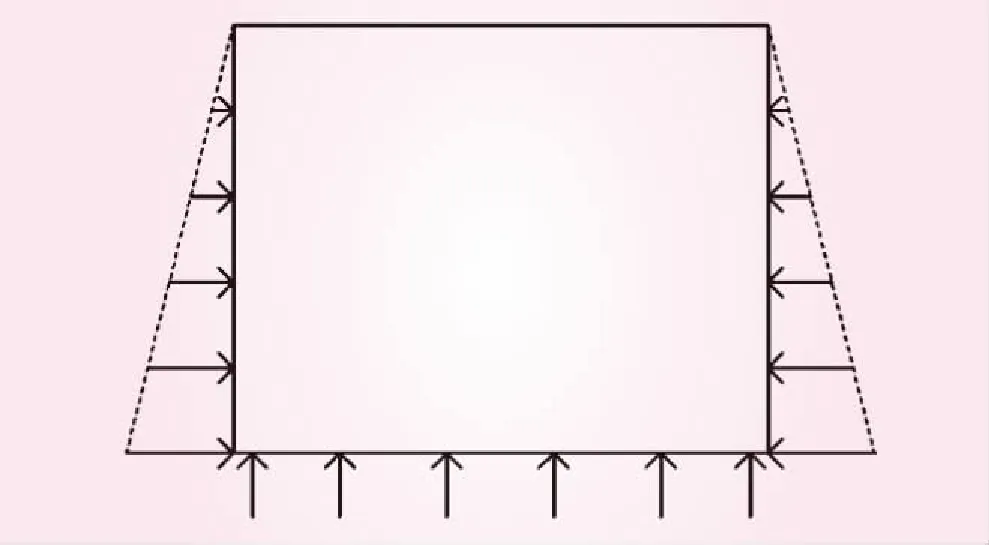
图3 快速应力边界法

3.2 侧压力系数实现

侧压力系数作为水平应力与竖向应力的比值，在研究过程中，单纯的改变比值大小显然无法得到好的效果。而快速应力边界法(S-B法)通过施加不同大小的应力，即应力边界条件的方式，直接改变水平应力与竖向应力，实现不同比例的侧压力，能够更好地满足实际分析的需要。同时，为了更好地体现侧压力系数对隧道变形的影响，避免出现侧压力系数较大、应力偏小从而对分析结果产生不良影响的情况，在进行应力边界施加时，需将竖向应力在勘测应力范围值内取一定值、水平应力在范围值内不断变化来实现不同的侧压力系数。

3.3 初始地应力场响应验证

根据地应力勘测资料，选取某处地应力场进行地应力场响应验证。该处模型底部应力σxx=σyy=5.28 MPa、σzz=3.31 MPa，分别用常规方法和快速应力边界法生成初始地应力场。为更加直观观测响应成果，仅取竖向应力云图做示例。图4为2种方法生成的竖向应力云图。从图4可知，常规方法生成的初始应力场模型底部应力σzz=2.54 MPa，远远不能满足实际需要；而快速应力边界法生成的初始应力场模型底部应力σzz=3.32 MPa，响应良好，与勘测数据基本吻合，能较好地满足实际需要。因此，通过此种方法实现初始地应力场的生成是切实有效的。

图4 生成的初始地应力场

4 实测数据对比分析

为了验证模型计算结果的准确性，使监测数据更加合理，将模型所得的监测结果与已有的实测数据进行对比分析。图5为开挖后某一时间段内实际施工中得到的某断面拱顶的沉降变形数据与模型计算所得数据的对比结果。从图5可以看出，模型计算结果与实测结果的变化规律整体上基本相似，开挖前6 d沉降变形增长率较快，产生的变形值占整体变形值的70%以上；随着时间的进行，变形增长速率逐渐降低，变形值将趋于稳定。因此，利用数值模拟软件对东天山隧道部分开挖段的模拟是较为成功的，所得到的结果是正确可信的。

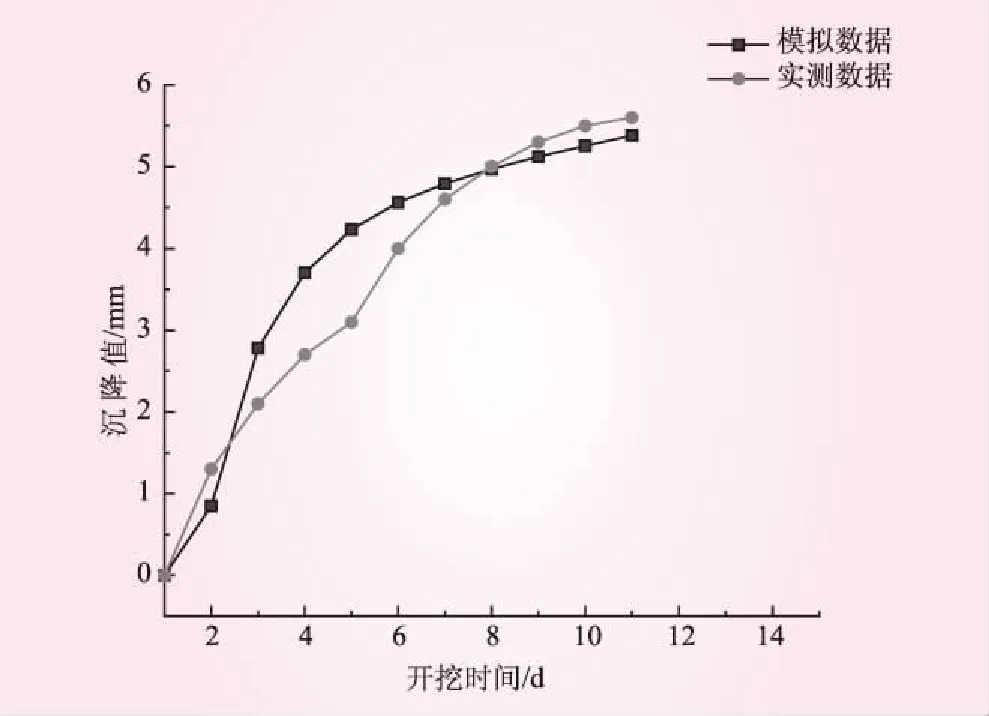
图5 实测数据与模型数据对比

5 变形分析

5.1 竖向变形

通过快速应力边界法生成不同侧压力系数λ下的初始地应力场，随后进行隧道模拟开挖；隧道开挖过程中的位移变形云图整体变化规律一致。限于篇幅，仅取λ=0.8时的云图做示例分析。λ=0.8时的位移云图见图6。从图6可知，隧道开挖产生的较大变形分布于拱顶与拱底处，在竖向和水平方向都存在一定范围的扰动。其中，隧道拱顶竖向变形的产生是由于隧道开挖卸荷破坏了围岩平衡，同时由于上部岩体的自重和构造应力共同作用下导致的。因此，在支护时对拱顶要及时安装衬砌结构，确保工程安全。拱底竖向变形主要是由于隧道开挖使岩层产生扩容膨胀，在力学作用下形成的隆起变形，变形程度较拱顶略小，但在施工过程中应同拱顶一起视作大变形区段进行有效衬砌，以保证隧道整体结构稳定。

图6 λ=0.8时的位移云图

图7是隧道在开挖过程中不同侧压力系数下拱顶和拱底产生的竖向变形。从图7可以看出，在不同的侧压力系数下，拱顶、底整体的竖向变形规律一致，随着侧压力系数的减小，竖向变形均呈现增大趋势。侧压力系数λ从0.8升至1.6，拱顶竖向变形值减小了约16%，拱底竖向变形值减小了约14%，表明此时隧道内围岩由竖向应力占主导作用逐渐变为水平应力占主导作用。

图7 不同侧压力系数下隧道竖向变形

隧道在开挖前5步内变形较为明显，变形增长速率较快，产生的变形值约占整体变形的82%。随着开挖的继续进行，拱顶、底变形增长速率降低，此时隧道已安装衬砌，表明所采用的衬砌系统对维持隧道整体稳定起到明显增强作用。进一步进行隧道开挖，监测点处的隧道变形基本趋于稳定，前方隧道开挖产生的扰动基本可以忽略不计，此时隧道围岩在衬砌系统的作用下已完成变形平衡，整体结构呈自稳定状态。因此，在后续隧道开挖过程中，侧压力系数较低的同类别工程区段要特别注意拱顶和拱底的较大变形，采用短进尺开挖，及时安装衬砌，建议局部采取钢支撑挂网喷锚支护，辅以超前锚杆支护，对不稳定块体及时进行锚固，以增强围岩稳定性，减小围岩变形。

5.2 水平变形

图8是隧道在开挖过程中不同侧压力系数下拱脚水平变形。从图8可知，随着侧压力系数λ从0.8升至1.6，隧道内围岩应力以水平应力占主导作用，拱脚的水平变形值从1.08 mm增长至3.37 mm。隧道在开挖的前3步内变形增长速率较快，且产生的变形值占整体变形的主体。在随后的开挖步中，随着衬砌系统的安装，隧道整体变形趋于稳定。由此可见，随着侧压力系数的增加，隧道拱脚处产生的变形增长相比于拱顶和拱底要更为明显，在施工中对于侧压力系数较大区段，拱脚处的支护强度要成倍数增长，及时支护。建议局部采取钢支撑挂网喷锚支护，同时采取随机锚固措施进行二次防护，以增强工程的安全性。

图8 不同侧压力系数下拱脚水平变形

5.3 沉降槽曲线

开挖过程中不同侧压力系数下隧道拱顶沉降槽曲线见图9。从图9可知，不同侧压力系数下的沉降槽曲线整体变形规律一致，最大变形值均在隧道轴线处，且随着侧压力系数的增加，隧道拱顶处变形值逐渐减小，与前文拱顶竖向变形的结论一致。沿水平方向，随着距隧道轴线距离的增加，隧道开挖过程中产生的沉降变形逐渐减小。

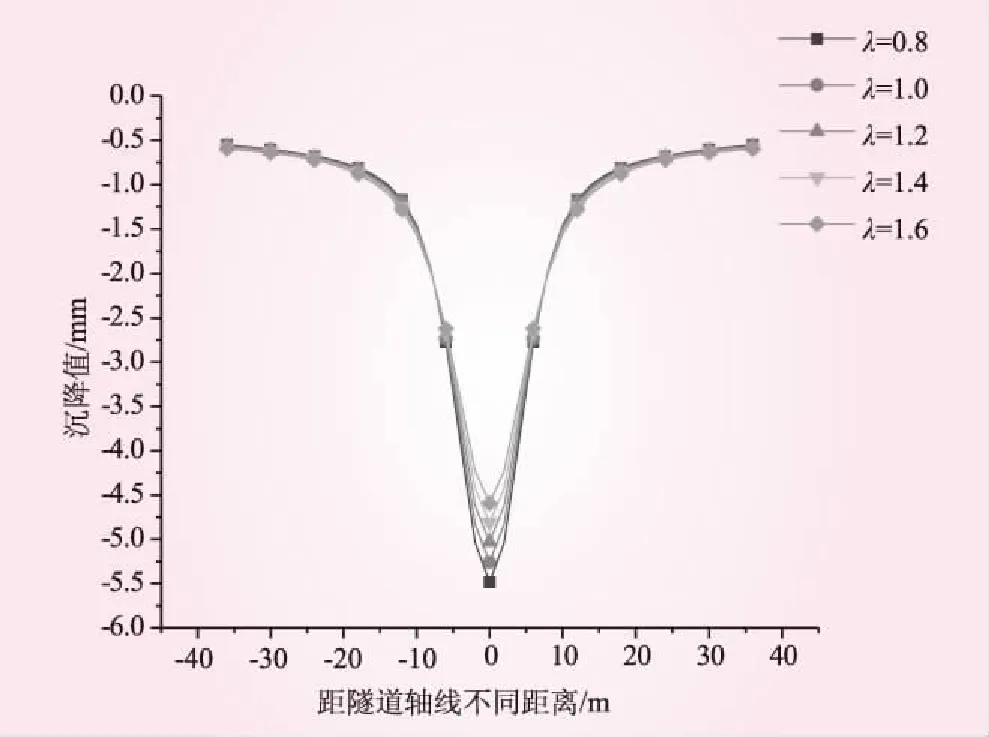
图9 不同侧压力系数下拱顶沉降槽

分别在距拱顶3R、6R和模型顶部设置监测点(监测点3～6)得到隧道变形数据，不同侧压力系数下沉降槽曲线见图10。从图10可知：

图10 不同侧压力系数下隧道沉降槽

(1)在隧道顶部，不同部位不同侧压力系数下的隧道变形规律保持一致，呈高斯分布，变形最大处均在隧道顶部轴线处；沿水平方向，随着距隧道轴线距离的增加变形值逐渐减小，隧道开挖产生的扰动逐渐减小；距轴线15 m处的变形速率开始降低，因此沿隧道水平方向上的开挖扰动范围为15 m处较佳。

(2)距隧道轴线20、28、32 m处隧道变形出现与隧道轴线处相反趋势，此时随着侧压力系数的增加变形值逐渐增加，并且从3R至模型顶部，随着埋深的减小变形值逐渐增大。这是由于随着距隧道轴线距离的增加，由隧道开挖破坏围岩平衡产生的变形逐渐减小，此时隧道在自重应力与构造应力共同作用下，岩体整体产生均匀沉降变形，在这部分变形中，隧道开挖扰动产生的变形值只占很小一部分，自重应力与构造应力占主导作用，由此产生这种相反的变化。3R、6R处和模型顶部不同位置的变形可以视为开挖隧道上部不同埋深处变形情况的体现，从3R处至模型顶部，随着埋深的减小，水平方向上的变形速率显著降低。

在不同侧压力系数下，不同埋深沉降槽曲线以及隧道埋深与变形关系曲线变化规律相似，限于篇幅，仅取λ=0.8时的情况进行分析。λ=0.8时的不同埋深沉降槽曲线见图11。λ=0.8时的隧道埋深与变形关系曲线见图12。从图11、12可知，竖直方向上，下方隧道开挖对模型顶部产生的扰动变形已非常小，且沉降变形与隧道埋深呈较好的线性关系。

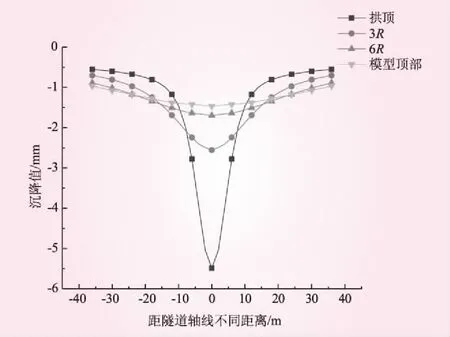
图11 不同埋深沉降槽

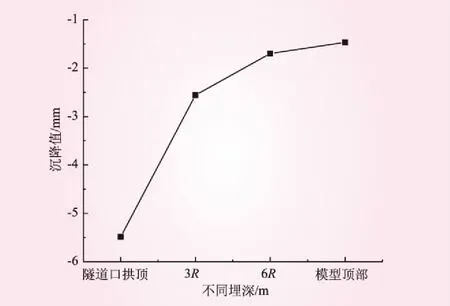
图12 隧道埋深与变形的关系

上部的扰动范围最理想情况为距拱顶60 m处，此时最大变形值约为隧道拱顶最大变形值的27%。在6R处产生的竖向变形值也较小，可以认为此处开挖产生的扰动较小，是较好的开挖非扰动范围，与以往数值模型研究上部边界取值范围为6R的结论一致。同时，水平和竖直开挖扰动范围的分析从侧面验证了本模型边界影响范围选择的正确性。

6 结 语

本文基于改进的初始地应力场的生成方法，分析不同侧压力系数λ下的隧道开挖变形规律，得出以下结论：

(1)隧道在开挖过程中拱顶的竖向变形最大，拱底次之。侧压力系数λ从0.8升至1.6，拱顶、拱底竖向变形值分别减小了约16%和14%，支护前变形占整体变形的82%。在侧压力系数较低的同类工程区段开挖过程中要注意拱顶和拱底的较大变形，采用短进尺开挖，及时安装衬砌系统，以增强围岩稳定性。

(2)随着侧压力系数λ从0.8升至1.6，拱脚水平变形值由1.08 mm增长至3.37 mm，变化率比拱顶和拱底要更为明显。在施工中对于侧压力系数较大区段，拱脚处支护建议局部采取钢支撑挂网喷锚支护，同时采用随机锚固措施进行二次防护，以增强工程的安全性。

(3)不同侧压力系数下的拱顶变形规律一致，呈高斯分布，随着距隧道轴线距离的增大，开挖扰动逐渐减小，变形速率显著降低；水平方向距隧道轴线15 m处和竖直方向6R处的扰动较小，是较为理想的非扰动范围。距拱顶60 m处围岩基本不受开挖影响，此时最大变形值约为拱顶最大变形量的27%。

(4)随着距隧道轴线距离的增加，开挖破坏围岩平衡产生的变形逐渐减小，隧道在自重与构造应力共同作用下使岩体整体产生均匀沉降变形，在这部分变形中，开挖扰动产生的变形只占很小一部分，自重应力与构造应力占主导作用，由此导致在3R、6R及模型顶部分别距轴线20、28、32 m处隧道变形出现与隧道轴线处相反的情况。