中外标准中混凝土强度接收准则对比分析*
2022-06-21李勇生蒋利学王卓琳
李勇生,蒋利学,王卓琳
(上海市建筑科学研究院有限公司,上海市工程结构安全重点实验室,上海 200032)
0 引言
贸易全球化和“一带一路”倡议的全面推进实施,对我国标准的国际化提出了更高要求。我国的工程建设标准需充分借鉴国际标准,尽可能采用国际通行的表现形式,展现我国工程建设标准与国际标准和国外先进标准的内在联系,提高我国工程建设标准的技术水平,以利于被国际市场理解、评估和采用,实现国际化。2017年实施的《中华人民共和国标准化法》,明确将根据标准的法律属性分为强制性国家标准和推荐性标准,其中强制性国家标准类似于国外的技术法规,推荐性标准为自愿采用性标准。这使我国标准化体系向着发达国家通行的“技术法规、技术标准”模式发展,为建立良好的标准化顶层设计、实现我国标准国际化奠定基础[1]。
改革开放以来,随着我国经济实力的快速增长和人民生活水平的日益提高,我国建筑结构设计标准对结构可靠度水平的要求逐步提高。根据文献[2]的分析,我国20世纪80年代系列设计规范对各类构件的可靠指标要求较接近统一标准[3]规定的目标可靠指标,21世纪00年代系列设计规范对各类构件的可靠指标要求总体已较目标可靠指标大0.5。GB 50068—2018《建筑结构可靠度设计统一标准》[3]对荷载分项系数进行调整后,各类构件的可靠指标要求总体已较目标可靠指标大0.8[4]。经历次设计标准修订后,对于结构构件的可靠度水平要求而言,我国标准与发达国家标准的差距已较小,这表明我国设计标准对结构构件的可靠度水平要求已基本与国际标准及发达国家标准接轨。但《建筑结构可靠度设计统一标准》指出,当前在材料和构件生产中,抽样检验标准多根据经验制定。其缺点在于未从统计学观点合理考虑生产方和用户方的风险水平或其他经济因素,因而规定的抽样数量和接收准则往往缺乏科学依据,标准的松严程度无法相互比较。
GB/T 50107—2010《混凝土强度检验评定标准》[5]规定混凝土强度可接收质量水平AQL具有95%的保证率(不合格品率p0=0.05),极限质量水平LQL具有60%的保证率(不合格品率p1=0.4)。而GBJ 107—87《混凝土强度检验评定标准》[6]规定极限质量水平LQL具有50%的保证率(不合格品率p1=0.5)。多位学者认为我国标准规定的混凝土强度接收准则要求较低,不利于保证工程质量和用户方利益。戴镇潮[7]认为验收时的混凝土强度平均值fm≥fk+kσ,其中,fk为混凝土强度标准值,σ为混凝土强度母体标准差,k为评定系数,当抽样样本容量为3~30时,对于一般结构k取3.12~2.11,对于重要结构k取3.33~2.18,可见k的取值明显大于1.645。蔡海等[8]根据GBJ 107—87《混凝土强度检验评定标准》对混凝土强度标准值的定义,认为混凝土强度是望大值,其极限质量强度标准值的下限即为fk,即检验批质量的不合格率上限为0.05。浦聿修等[9]认为GBJ 107—87《混凝土强度检验评定标准》对混凝土强度不合格母体均值的取值偏低,建议极限质量的保证率取70%~75%。王华琪等[10]认为极限质量是可接收的最差质量,其为从用户方角度考虑的参数,p1取值太大无法较好地保护用户方利益,p1取值太小则会造成不必要的抽样成本增加。对于混凝土强度,建议取p0=0.05,p1=0.2,即极限质量的保证率取80%。
综上所述,我国标准规定的混凝土强度接收准则要求太低,且受到了较多质疑,不利于保证工程质量、降低用户方风险,与设计标准不断提高结构构件可靠度水平的做法不协调。接收准则尚缺乏科学依据,不利于与国际接轨。本文对我国、美国、英国5本标准中的混凝土强度接收准则进行对比分析,比较极限质量水平、OC曲线和检验功效、非统计方法与统计方法的检验功效一致性,分析最小值接收准则的必要性与合理性,为我国混凝土强度验收实践和标准修订提供参考。
1 中外标准中的混凝土强度接收准则与分析
1.1 我国标准的规定
1.1.1GB/T 50107—2010《混凝土强度检验评定标准》
GB/T 50107—2010《混凝土强度检验评定标准》将检验批的混凝土强度接收准则分为标准差已知统计方法(σ法)、标准差未知统计方法(s法)和非统计方法。当连续生产的混凝土,生产条件在较长时间内保持一致,且同一品种、同一强度等级混凝土的强度变异性保持稳定时,可对连续3组试件的强度按σ法进行评定,此时标准差采用前一检验批的标准差σ(要求前一检验批样本容量≥45)。不符合上述条件,但样本容量≥10时,可采用s法进行评定,此时的标准差采用样本标准差s;当样本容量<10时,应采用非统计方法。3类方法均需同时对混凝土强度平均值fm和最小值fmin进行评定,如表1所示。

表1 GB/T 50107—2010《混凝土强度检验评定标准》接收准则
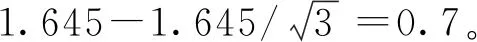
1.1.2JTJ 221—98《港口工程质量检验评定标准》
JTJ 221—98《港口工程质量检验评定标准》[12]对混凝土强度接收准则的规定如表2所示。

表2 JTJ 221—98《港口工程质量检验评定标准》接收准则
《港口工程质量检验评定标准》中未规定σ法。s法虽也根据样本容量分为3档(最小样本容量n=5),但对于混凝土强度平均值接收准则统一取k=1.0,仅混凝土强度最小值接收准则有所区别。
非统计方法的样本容量n=2~4,混凝土强度平均值采用fm≥fk+σ的接收准则,可见评定系数k仍取与s法相同的值1.0,但标准差σ取混凝土强度标准差的平均水平,即混凝土强度等级
1.1.3TB 10425—2019《铁路混凝土强度检验评定标准》
TB 10425—2019《铁路混凝土强度检验评定标准》[13]对混凝土强度接收准则的规定如表3所示。
《铁路混凝土强度检验评定标准》也规定了σ法、s法和非统计方法。σ法要求样本容量n=4,且前一检验批样本容量≥48,评定系数k=0.82,这3个条件均略较GB/T 50107—2010《混凝土强度检验评定标准》严格;s法和非统计方法与GB/T 50107—2010《混凝土强度检验评定标准》规定相同,不再详述。
1.2 美国标准的规定
美国标准ACI 318—05Buildingcoderequirementsforstructuralconcreteandcommentary[14]中出现了“规定的抗压强度f′c”概念,但未明确“规定的抗压强度f′c”的保证率,这与我国标准规定的混凝土强度标准值和英国标准规定的混凝土强度特征值明确具有95%的保证率不同。该标准规定的接收准则如表4所示,规定的统计方法未区分σ法和s法,认为样本容量n≥30时样本标准差s可代替母体标准差σ,其平均抗压强度f′cr采用以下接收准则:f′cr=f′c+1.34s,其中,系数1.34是根据连续3组试件的平均抗压强度低于f′c的概率为1%计算得到的,f′c实质上具有91%的保证率[15]。

表4 ACI 318—05 Building code requirements for structural concrete and commentary 接收准则
另外,该标准规定当f′c≤35MPa时,任意一组混凝土抗压强度(最小值)+3.5MPa
该标准还规定当样本容量n=15,20,25时,计算得到的样本标准差s应分别乘以修正系数1.16,1.08,1.03;当样本容量n<15时,采用非统计方法,并根据混凝土强度等级分为3档。
1.3 英国标准的规定
英国标准BS EN 206-1∶2013Concrete—Part1:specification,performance,productionandconformity[16]规定对于连续生产的情况,当样本容量n≥15时,按σ法评定混凝土强度平均值(界限1),评定系数k=1.48;对于初期生产情况,当样本容量n=3时,按非统计方法评定混凝土强度平均值。2种情况下均需评定最小值(界限2),如表5所示。

表5 BS EN 206-1:2013 Concrete—Part 1: specification, performance, production and conformity 接收准则
确认某单独批混凝土是否属于同类混凝土时,对该批测试结果的平均值按表6的验收界限(界限3)进行评定。当验收不通过时,不应将该批混凝土划为同类混凝土,应独立进行评定。

表6 同类混凝土各批的验收界限
标准差σ通过前3个月的至少35个连续测试结果计算得到。在后续生产中应验证该标准差的有效性,当根据最近15个数据计算的标准差s15符合0.63σ≤s15≤1.37σ时,通过验证,否则应根据最近的35个数据重新计算确定σ的估计值。
2 平均值统计方法接收准则的对比分析
由上述分析可知,中外5本标准有以下共同特征。
1)多数标准规定了统计方法和非统计方法,统计方法用于样本容量较大时,非统计方法用于样本容量较小时。
2)多数标准采用平均值和最小值联合接收准则,且无论样本容量多大,均需同时符合平均值和最小值接收准则。其中,美国标准已将最小值接收准则改为另一类平均值接收准则,即2个平均值联合接收准则。
3)在统计方法的平均值接收准则中,符合性评定系数k为0.7~1.55,差异较大,但均<1.645,说明其等效保证率均<95%。
通过分析,需重点关注以下问题。
1)抽样检验中生产方风险和用户方风险平衡问题,等效保证率(由评定系数k确定)和抽样数量取值问题。
2)非统计方法参数确定问题。
3)最小值接收准则必要性及其参数设置问题。
2.1 标准抽样方案
产品抽样检验多采用保护生产方利益的接收准则,这是国际、国内各行业通行的准则[17]。2类风险的一般控制范围为:α=1%~5%,β=5%~10%。从适当保护生产方利益的准则来看,β取值略大于α是合理的。我国GB 50300—2013《建筑工程施工质量验收统一标准》[18]规定,对于主控项目,α,β均宜≤5%;对于一般项目,α宜≤5%,β宜≤10%。混凝土抗压强度属于混凝土结构中的主控项目,故GB/T 50107—2010《混凝土强度检验评定标准》规定α,β均宜≤5%。
我国标准对混凝土强度标准值提出了具有95%保证率的明确定义,可接收质量水平AQL对应的不合格品率p0=0.05,对此并无争议。争议的焦点主要集中在对极限质量水平LQL的规定上,GB/T 50107—2010《混凝土强度检验评定标准》规定LQL应具有不低于60%的保证率,即不合格品率p1=0.4。本文对该极限质量水平LQL的合理性进行分析,根据文献[17],由“不合格品率p0对应的错判概率为α,接收概率为(1-α)”和“不合格品率p1对应的漏判概率为β,接收概率为(1-β)”条件联合求解抽样样本容量n和评定系数k,当标准差已知时(σ法),有:
(1)
式中:Φ-1(α)为错判概率α标准正态分布函数Φ(α)的反函数;Φ-1(β)为漏判概率β标准正态分布函数Φ(β)的反函数;Φ-1(p1)为LQL对应的不合格品率p1标准正态分布函数Φ(p1)的反函数;Φ-1(p0)为AQL对应的不合格品率p0标准正态分布函数Φ(p0)的反函数。
(2)
确定n和k后,可计算对应于不同不合格品率p的接收概率L(p):
(3)
当标准差未知时(s法),有:
(4)
(5)
(6)
对比2种条件下的n,k,L(p)可知,s法的n大于σ法,s法与σ法的k完全相同,L(p)则有明显区别。
设合格质量对应的不合格品率p0=0.05,在不同极限质量水平(p1取不同数值)下,计算得到的n和k如表7所示。
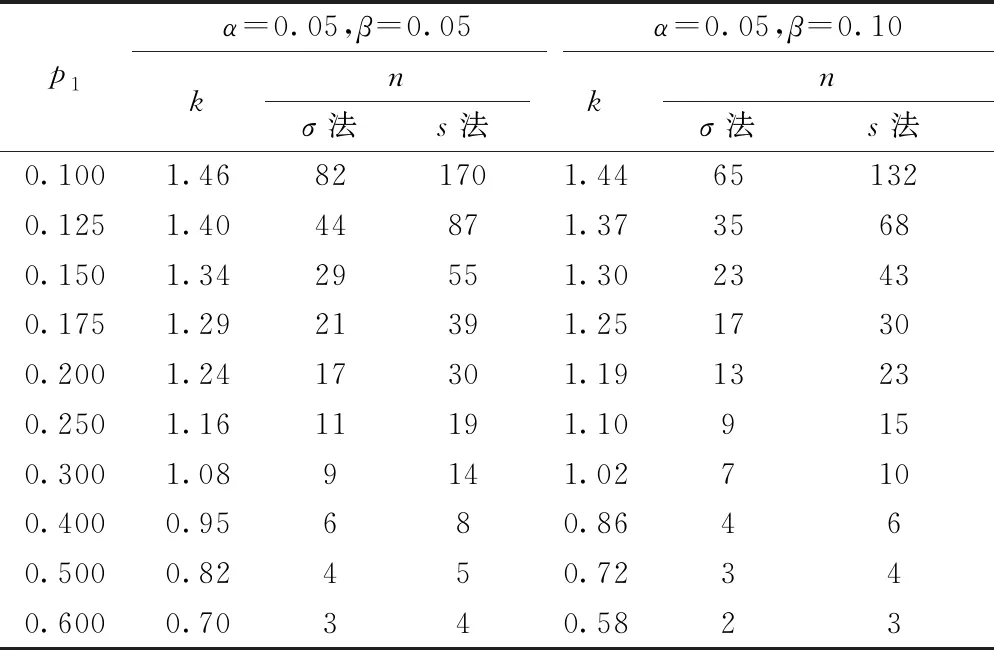
表7 不同极限质量水平下的抽样方案
按GB/T 50107—2010《混凝土强度检验评定标准》的规定,α=0.05,β=0.05,k=0.70,n=3(σ法)对应的p1=0.6,即极限质量水平的保证率仅为40%,未达到该标准规定的60%的水平。即使在α=0.05,β=0.10的条件下,k=0.72,n=3(σ法)对应的p1=0.5,极限质量水平的保证率为50%,仍未达到该标准规定的60%的水平。采用s法时,该标准的k,n组合不符合表7中α=0.05,β=0.05时的标准抽样方案,且对应的p1小于σ法,即极限质量水平的保证率高于标准差已知方案。
在α=0.05,β=0.05的条件下,《铁路混凝土强度检验评定标准》规定的σ法抽样方案(k=0.82,n=4)对应的p1约为0.5,即极限质量水平的保证率为50%。《港口工程质量检验评定标准》规定n≥5时s法的k取1.0,显然不是标准抽样方案。
美国标准未区分σ法和s法,当n=30时,因样本容量足够大,可近似假定s=σ,k取1.34时,该抽样方案大致对应于α=0.05,β=0.05条件下的p1=0.15,即极限质量水平的保证率为85%。可见美国标准的抽样方案(k=1.34,n=30)大致符合标准抽样方案。
英国标准的σ法抽样方案(k=1.48,n=15)不符合标准抽样方案,其中k=1.48的取值过大(p1仅为0.1),而n=15的取值过小,与k=1.48不匹配。
2.2 OC曲线与检验功效分析
我国标准GB/T 50107—2010《混凝土强度检验评定标准》中各统计方法的OC曲线对比如图1所示。由图1可知,σ法抽样方案(k=0.70,n=3)的OC曲线较平坦,检验功效较差,p0=0.05时的接收概率为0.95,但L(p)=0.05时的p1高达0.6。相对而言,各s法抽样方案的检验功效均较好,L(p)=0.05时的p1集中在0.3附近,而L(p)=0.95时的p0为0.03~0.1。
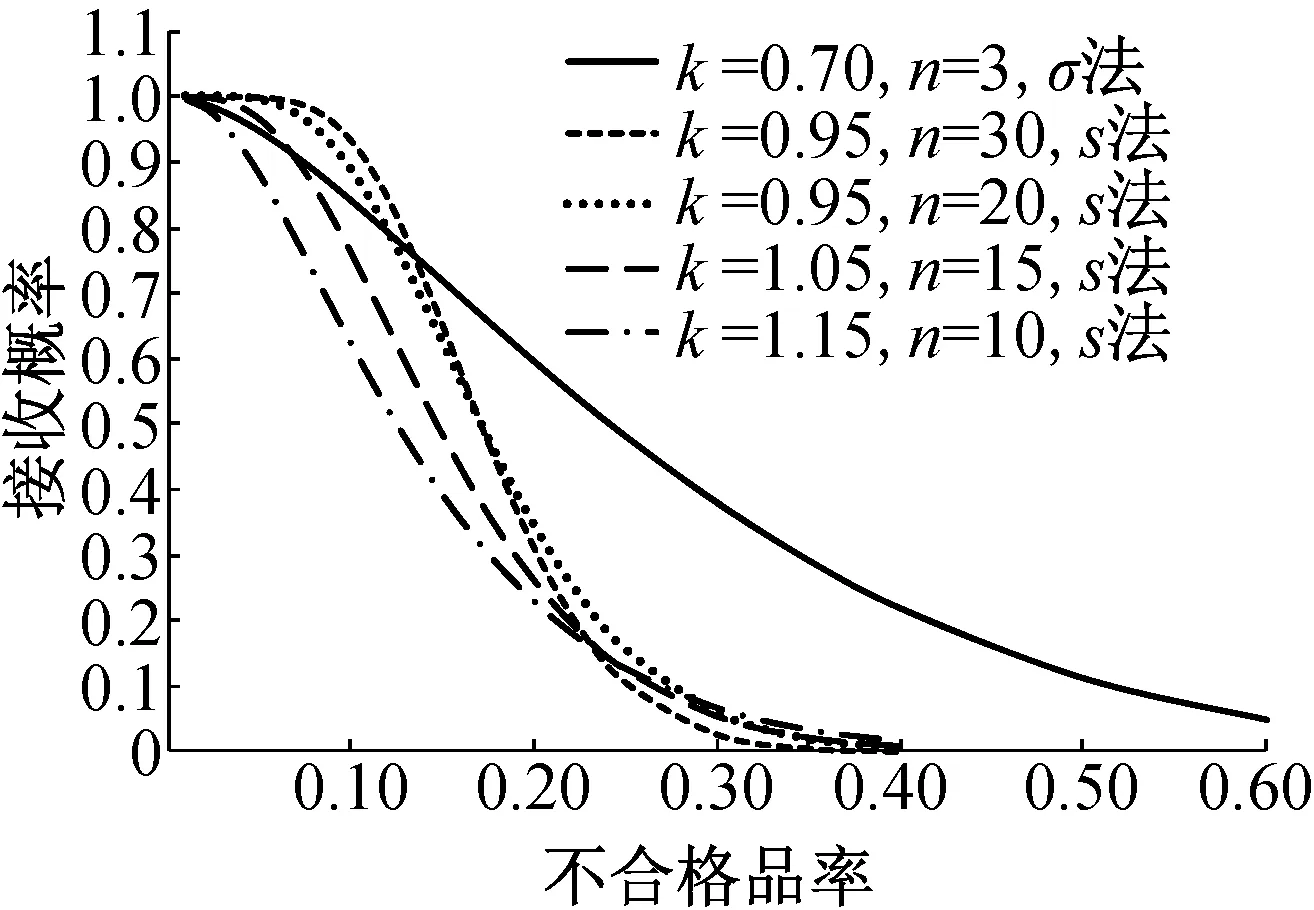
图1 GB/T 50107—2010《混凝土强度检验评定标准》各统计方法OC曲线对比
中外标准中σ法OC曲线对比如图2所示,其中,美国标准的抽样方案(k=1.34,n=30)等同为σ法。由图2可知,国内标准的OC曲线差异较小,p0=0.05时的接收概率均为0.95,其中《港口工程质量检验评定标准》中L(p)=0.05时的p1为0.5,GB/T 50107—2010《混凝土强度检验评定标准》中L(p)=0.05时的p1为0.6。美国、英国标准的OC曲线差异较小,p1=0.15时的接收概率均为0.05,美国标准中L(p)=0.95时的p0为0.05,英国标准中L(p)=0.95时的p0为0.03。中外标准的OC曲线差异较大,国外标准的检验功效明显好于国内标准。

图2 中外标准中σ法OC曲线对比
中外标准中s法OC曲线对比(n=15)如图3所示,其中,英国标准的抽样方案(k=1.48,n=15)是假设的s法方案。由图3可知,国外标准的检验功效明显好于国内标准。国内标准中L(p)=0.05时的p1为0.3~0.35,L(p)=0.95时的p0为0.06~0.07;国外标准中L(p)=0.05时的p1为0.18~0.2,L(p)=0.95时的p0为0.01~0.02。

图3 中外标准中s法OC曲线对比(n=15)
3 平均值非统计方法接收准则对比分析
GB/T 50107—2010《混凝土强度检验评定标准》中非统计方法样本容量n的适用范围为<10,《港口工程质量检验评定标准》中非统计方法样本容量n的适用范围为2~4,美国标准中非统计方法样本容量n的适用范围为<15,英国标准中非统计方法样本容量n的适用范围为3。除英国标准非统计方法的样本容量与统计方法不衔接外,其余3本标准非统计方法的样本容量均与统计方法衔接。
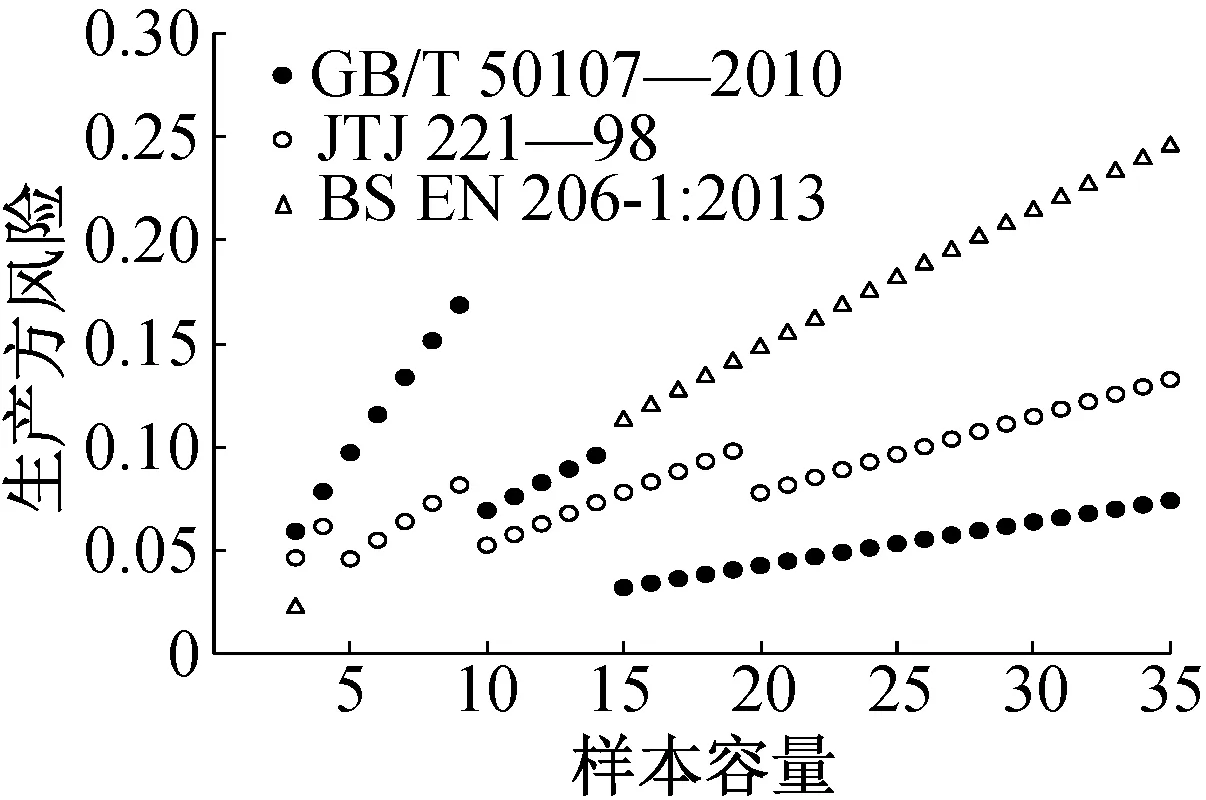
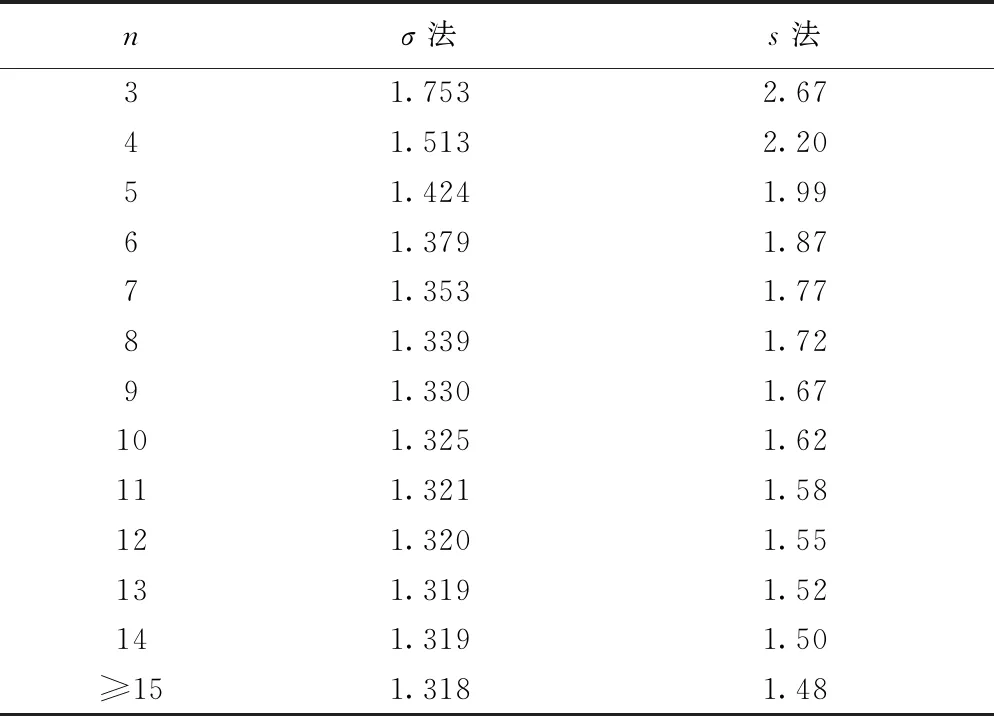
中外标准中非统计方法有3种不同的表示方式,其中美国标准和英国标准采用fm≥fk+Δ的差值法表示(Δ为差值),《港口工程质量检验评定标准》采用fm≥fk+kσ0的类似统计方法表示(σ0为平均质量水平的标准差),GB/T 50107—2010《混凝土强度检验评定标准》采用fm≥λfk的系数法表示。现假定平均质量水平的标准差σ0取值如下:当混凝土强度等级 图4 中外标准非统计方法对比 从统一的数理统计学观点来看,由于非统计方法的样本容量小于统计方法,非统计方法的评定系数k取值大于统计方法才是合理的。对比同一标准的统计方法和非统计方法的k值可知,GB/T 50107—2010《混凝土强度检验评定标准》中非统计方法k值差异较大,混凝土强度等级为C15~C25时的k为0.64~0.83,与σ法的k=0.7相当;混凝土强度等级为C30~C35和C60~C80时的k为1.0~1.17,大致与s法的取值相当;而混凝土强度等级为C40~C55时的k为1.23~1.50,大于s法的取值。《港口工程质量检验评定标准》中非统计方法取k=1.0,与s法完全一致。美国标准中非统计方法的k为1.63~2.0,大于s法;英国标准中非统计方法的k为0.5~1.14,明显小于σ法的k=1.48。可见,除美国标准的2类方法具有较统一的数理统计学原则外,其余标准的2类方法数理统计学原则均不一致。 最小值评定旨在防备可能出现的局部质量下降、实际标准差过大的情况,或避免出现强度过低的情况[5]。最小值评定属于一次计数抽样方案,与平均值评定联合使用,可提高生产方的风险,降低用户方的风险。其与样本容量n的关系较大,n越大,出现不满足最小值评定条件的可能性越大。因此,最小值评定条件起辅助调节作用,其参数的确定需合理。 图5 中外标准中最小值评定系数k′对比 根据一次计数抽样原理,可根据k′值计算样本容量n不同时的生产方风险α: α=1-[Φ(1.645+k′)]n (7) 根据图5中的k′值和式(7)计算生产方风险,结果如图6所示。由图6可知,在任意中外标准的参数条件下,随着样本容量n的增大,当k′值相同时,生产方风险基本呈线性增大的趋势;随着n的增大,提高k′值有助于降低生产方风险,但相邻n之间的生产方风险有不连续现象。因此,是否需要设置最小值评定条件存在较大争议。文献[19]指出,如最小值接收准则设置过于严格,会限制平均值接收准则的作用;如最小值接收准则设置过于宽松,起不到应有作用。为使生产方风险保持基本一致,k′值需根据n值分为多档,最理想的情况是根据确定的生产方风险α、样本容量n和式(7)反算k′: 图6 中外标准中最小值接收准则生产方风险对比 (8) Taerwe[20]认为,当n和σ均较小时,由于最小值接收准则和平均值接收准则之间的相关性,最小值接收准则的功效可忽略;当n较小而σ较大时,最小值接收准则的作用增大,其功效接近于平均值接收准则,2种接收准则互补;当n较大时,最小值接收准则的功效较低,即可被最小值接收准则拒收的检验批早已被平均值接收准则拒收。Taerwe认为设置最小值接收准则的必要性较小,建议统一采用fm≥fk+ks的平均值接收准则,即将英国标准中统计方法n≥15的条件放松至n≥3,并建议评定系数k的取值如表8所示。 表8 评定系数k的建议取值 综合上述分析,我国标准规定的极限质量水平明显偏低,导致混凝土强度接收准则明显低于国外标准,OC曲线反映的检验功效低于国外标准,不利于保证工程质量、降低用户方风险,且不利于与国际标准接轨。中外多数标准的平均值接收准则不符合一次计数抽样检验理论,标准差未知统计方法、非统计方法与标准差已知统计方法的检验功效差异较大;多数情况下无须同时设置平均值接收准则和最小值接收准则。美国标准OC曲线反映的检验功效较好,平衡了生产方风险和用户方风险,等效保证率略>90%,统一了标准差已知统计方法和标准差未知统计方法,非统计方法与统计方法采用的数理统计原则较一致。 参考美国标准的做法,结合我国标准的传统习惯,提出我国混凝土强度接收准则初步改进建议。 1)以一次计数抽样检验理论和我国标准“混凝土强度标准值应具有95%保证率”的定义(p0=0.05)为依据,确定合理的生产方风险、用户方风险和极限质量水平,确定标准差已知的抽样方案。综合平衡生产方风险和用户方风险,并适当考虑保护生产方的利益,等效保证率取值宜为90%左右。 2)以贝叶斯理论为依据,与标准差已知方案保持一致的分位值,确定对应于不同样本容量n的评定系数k,确定标准差未知时的抽样方案(k,n)。 3)由于样本容量n较小时,无法估计较精确的标准差s,可改用非统计方法,即确定平均质量水平的标准差σ0和统一的评定系数k,并以一次计数抽样理论为依据,确定最小值评定系数k′,作为平均值接收准则的补充,防止出现标准差过大的不利情况。 4)当样本容量较小时,即使采用标准差已知抽样方案,OC曲线检验功效不理想,既不利于保护生产方利益,又不利于保护用户方利益。此时,可采用贝叶斯理论的思想,将前一检验批与本次检验批样本合并,以扩大样本容量,提高检验功效。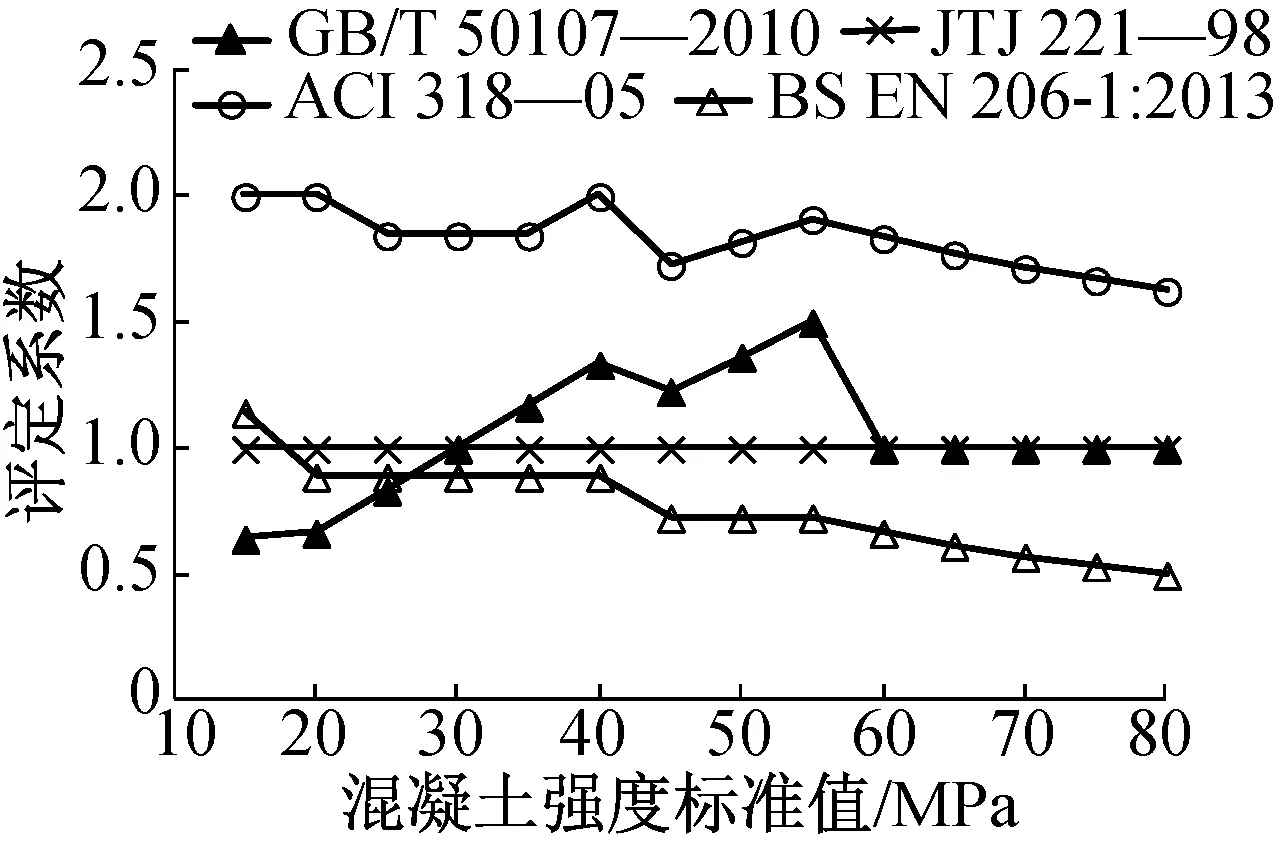
4 最小值接收准则对比分析


5 对我国混凝土强度接收准则的初步改进建议
