考虑渗透系数随时间变化及固结状态影响的一维固结计算

金超奇，徐长节，江平，颜建伟，程超，章立辰

(1. 华东交通大学 江西省岩土工程基础设施安全与控制重点实验室；土木工程国家实验教学示范研究所，南昌 330013；2. 江西省港航建设投资集团港航运输有限公司，南昌 330008)

中国的交通网络不断发展，高速铁路网由“四纵四横”发展为“八纵八横”，软土路基上高速公路、铁路等工程建设问题也越来越多。其中，路基沉降是工程质量控制的关键环节，因此，准确合理的预测方法对软土路基的固结沉降非常重要。经典太沙基(Terzaghi)一维固结理论能快速地预估地基沉降，但常常与实测值存在较大的误差[1-2]。主要原因是Terzaghi一维固结理论是基于常固结系数Cv的假设，而实际上，在固结过程中，固结系数Cv中的渗透系数k、压缩系数av以及孔隙比e都会随着固结应力和时间发生变化。

20世纪末，Ducan[1]和Olson[2]都曾指出，固结系数的不确定性是传统固结理论计算的局限性的根本原因。据此，Li等[3]假设压缩系数和渗透系数同时变化，推导了在线性加载过程中黏土的一维非线性固结方程。Dumais等[4]通过非线性有效应力、孔隙比及渗透系数之间的关系，推导了融化土固结的一维计算模型。Cai等[5]利用双曲线拟合方法，得到了一种修正的固结系数预测模型。Li等[6]研究了固结系数随固结应力及时间的变化规律，发现随着固结应力的增加，固结系数并非单调的变化趋势，而是先增后减。Liu等[7]和Desai等[8-9]利用修正剑桥本构模型来描述土体固结行为。王珏等[10]发现一维固结沉降的发展与土体参数及荷载相关，弹性模量越大，沉降量越小；黏弹性体的延迟时间越大，固结变化越慢。阮永芬等[11]认为土体的沉积作用和应力历史会影响地基固结沉降的确定。夏长青等[12]和胡安峰等[13]认为固结过程中压缩性与渗透性线性相关，推导出了饱和软土地基一维非线性固结解析解。

目前，学者们对于Terzaghi一维固结理论已开展了很多研究，部分学者[14-17]在研究固结系数Cv的变化时，认为孔隙比e的变化由固结应力大小和固结状态决定，而孔隙比e在固结过程中随时间的变化方面的研究还相对缺乏。针对上述问题，笔者考虑了在固结应力作用下固结系数Cv的变化、孔隙比e随时间的变化，同时也考虑了土的固结状态(正常固结土、超固结土、欠固结土)及修正后的渗透系数预测公式，得到修正的Terzaghi一维固结理论。首先，基于工程常用的5种渗透系数预测公式和侧限压缩量公式，结合不同初始固结状态的e-lgp压缩曲线关系，对5种渗透系数预测公式进行修正，构建了考虑渗透系数随时间变化及固结应力影响的渗透系数预测公式kt，再将所构建的渗透系数计算式代入固结系数Cv中，对经典Terzaghi一维固结理论进行修正；然后，利用高俊等[14]、张乐等[15]的试验数据探究预测公式的适用性和可靠性；最后，通过工程案例讨论修正后的Terzaghi一维固结理论的合理性，并与不考虑时间的固结方程进行对比。

1 渗透系数预测公式的修正

1.1 考虑渗透系数与时间的相关性

以孔隙比、颗粒直径和级配等重要影响因素[18-19]所构建的渗透系数预测公式为基础，考虑时间相关性，如达西渗透系数公式、柯森-卡门渗透系数公式、太沙基渗透系数公式、中国水利水电科学研究院渗透系数公式、斯托克斯孔隙流渗透系数公式等[20]。结合固结度和侧限压缩量的关系，推导出固结应力作用下某一时刻t孔隙比et的表达式，同时，考虑土的初始固结状态(正常固结土、超固结土、欠固结土)，对上述渗透系数预测公式进行修正，构建考虑渗透系数随时间变化及固结应力影响的渗透系数预测公式。

1)达西渗透系数预测公式

(1)

式中：d为颗粒粒径，cm；β为颗粒的球体系数，圆球时取π/6；λ为邻近颗粒的影响系数，圆球取3π。

2)柯森-卡门渗透系数预测公式

(2)

式中：ρwz为自由水的密度，g/cm3；c2为与颗粒形状及水的实际流动方向有关的系数，约为0.125；s为土颗粒的比表面积，cm-1；η为自由水的动力黏滞系数，g·s/cm2。

3)太沙基渗透系数预测公式

(3)

式中：d10为粒径分布曲线上纵坐标为10%时所对应的土颗粒粒径，cm。

4)中国水利水电科学研究院渗透系数预测公式

(4)

式中：d20为粒径分布曲线上纵坐标为20%时所对应的土颗粒粒径，cm。

5)斯托克斯孔隙流渗透系数预测公式

(5)

式中：R为毛细管的半径，cm。

在实际工程中，上述预测公式中土的物理参数往往不易测得，且在固结过程中一般不会发生变化，而初始渗透系数k0和初始孔隙比e0可以由勘测资料获得，因此，用k0和e0对上述参数进行代换。

(6)

(7)

(8)

(9)

(10)

再分别将式(6)～式(10)代入式(1)～式(5)中，得到的渗透系数预测式(11)～式(15)能基于初始渗透系数k0和初始孔隙比e0对土的渗透系数进行快速准确地计算。

(11)

(12)

(13)

(14)

(15)

式中：kt为某一时间t的渗透系数；et为某一时刻t的孔隙比。

在固结过程中，孔隙比et会随时间逐渐达到e∞，因此，为了体现孔隙比et与时间的相关性，需要加入固结度Ut这一概念。所谓固结度Ut，是指在某一时间t后，土体发生固结或者孔压消散的程度。

St=UtS∞

(16)

式中：St是某一时刻的沉降量；S∞是固结完成后的沉降量。

将侧限压缩量公式代入式(16)，然后将式(17)整理，得到某一时间t的孔隙比et的表达式式(18)。

(17)

et=e0-Ut(e0-e∞)

(18)

式中：e∞是固结完成后的孔隙比。

将式(18)代入式(11)～式(15)，得到修正后的渗透系数预测公式

(19)

(20)

(21)

(22)

(23)

根据式(19)～式(23)可知，渗透系数kt是关于固结度Ut(时间相关)和孔隙比e∞的函数，而孔隙比e∞需要由固结应力和土的初始固结状态共同确定。不同土的初始固结状态不同，e-lgp压缩曲线也不同，因此，还需要对不同土的初始固结状态进行讨论。

1.2 考虑固结状态及固结应力

土层的不同固结状态对应着不同的e-lgp压缩曲线，根据前期固结应力σc和现有有效应力σ0的关系，可将土体分为正常固结土，超固结土和欠固结土。

正常固结土的压缩曲线如图1所示。

(24)

式中：Cc为压缩指数。

图1 正常固结状态的e-lg p压缩曲线Fig.1 e-lg p compression curve of normal consolidation

超固结土的压缩曲线如图2所示。

当σ0≤σ0+Δσ≤σc时，有

(25)

当σ0+Δσ≥σc时，有

(26)

式中：Ce为回弹指数。

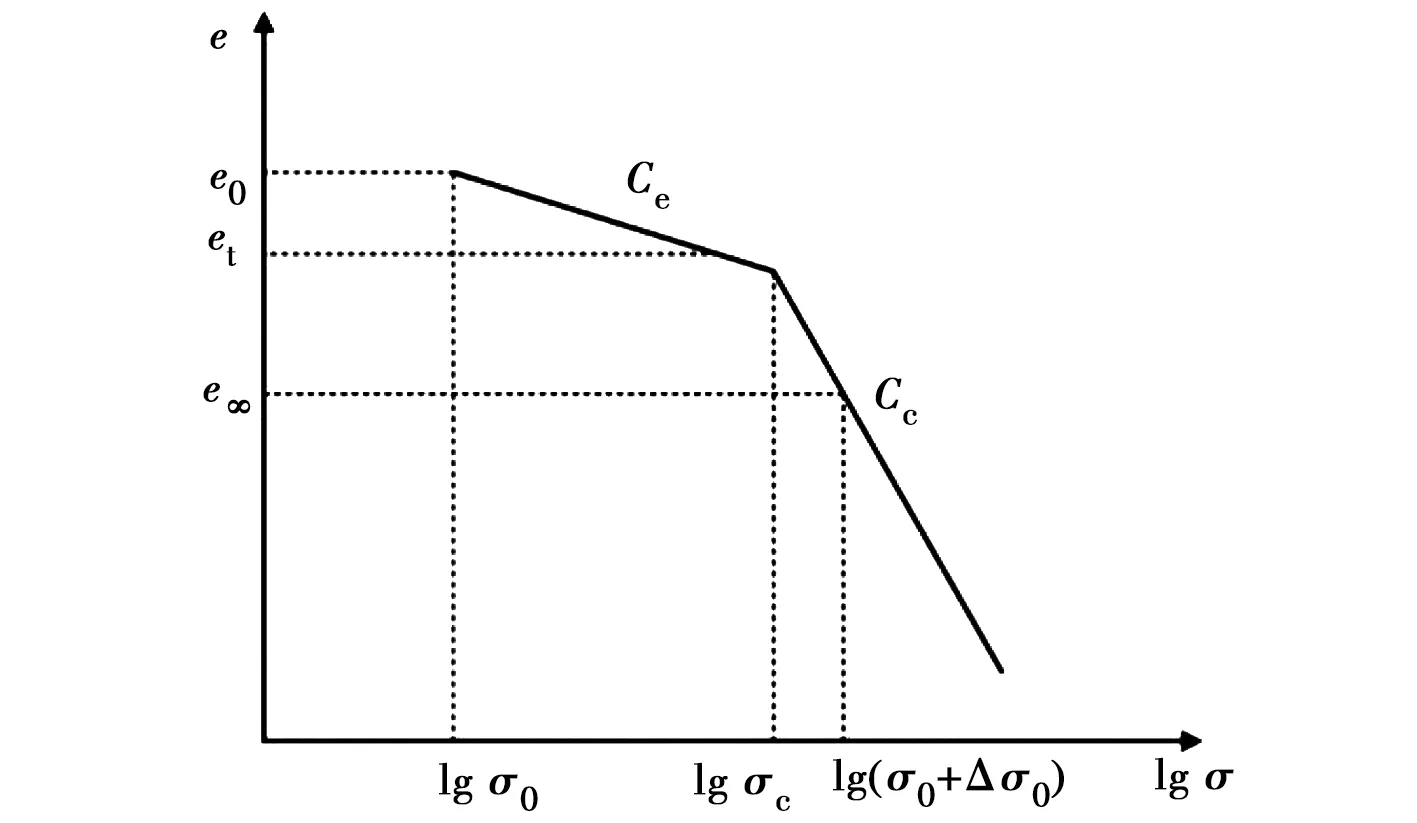
图2 超固结状态的e-lg p压缩曲线Fig.2 e-lg p compression curve under over consolidation

欠固结土的压缩曲线如图3所示。

(27)

通过不同的e-lgp压缩曲线，得到固结应力下相应的孔隙比e∞。再分别将式(24)～式(27)代入式(19)～式(23)中，便可得到针对不同土初始固结状态下的渗透系数公式。例如：正常固结土的柯森-卡门渗透系数修正公式

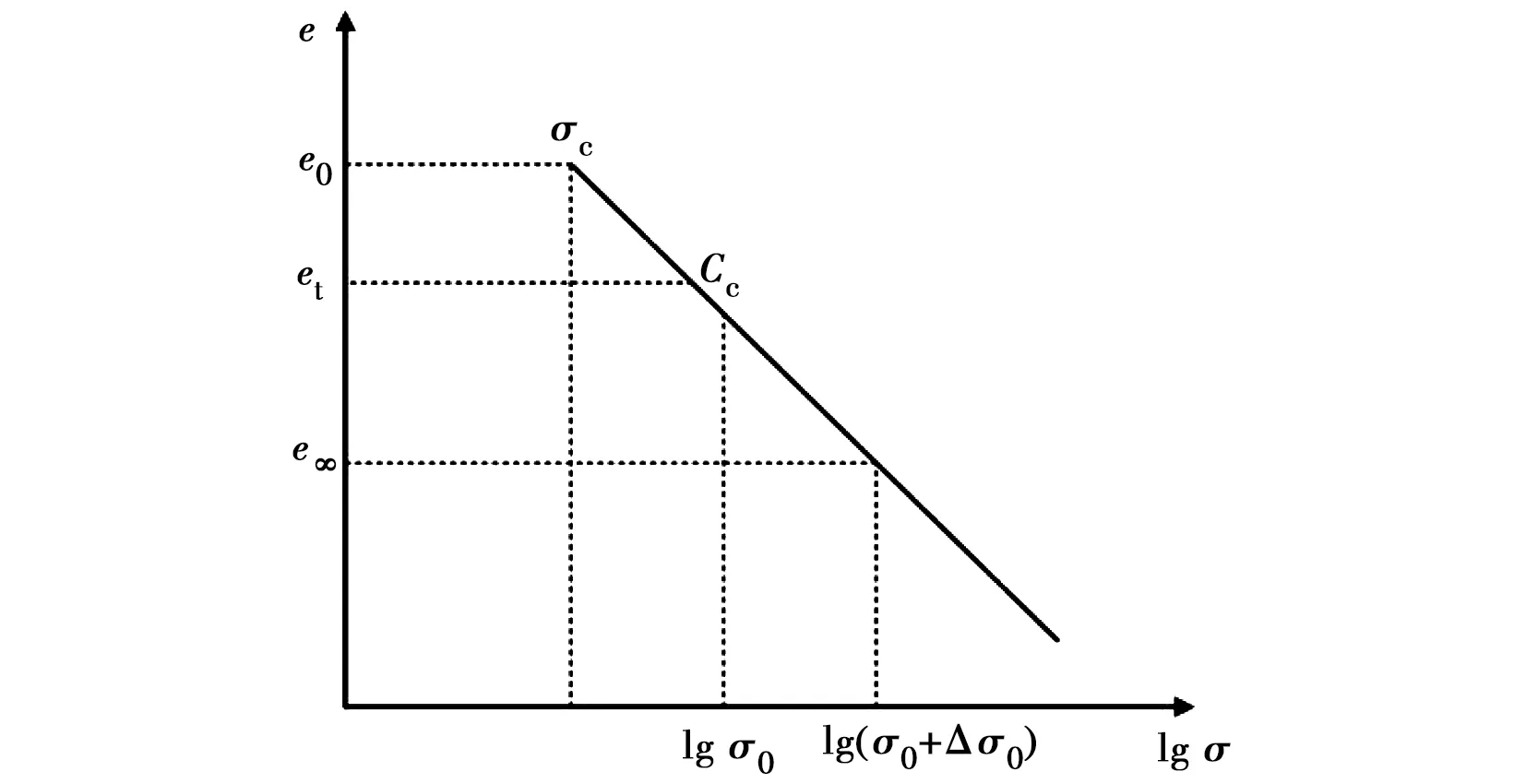
图3 欠固结状态的e-lg p压缩曲线Fig.3 e-lg p compression curve of under consolidated

(28)

由式(28)求渗透系数kt，最后还需要确定固结度Ut。因此，接下来介绍经典太沙基(Terzaghi)一维固结理论，并对其进行修正，最后与上述修正后的渗透系数公式进行联立求解。

2 Terzaghi一维固结理论修正

Terzaghi固结理论假定，对于饱和土来说，在dt时间内单元体体积的减小应变等于单元体中水的净出流量，即

(29)

式中：mv为体积压缩系数。

在t时刻通过单元体的流量

(30)

将式(30)代入式(29)即可得

(31)

Cv=k(1+e0)/avγw

(32)

根据边界条件及初始条件

t=0、0≤z≤H时，u0=p

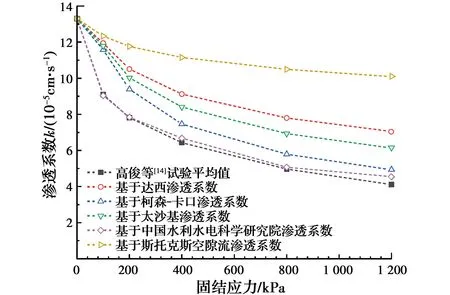
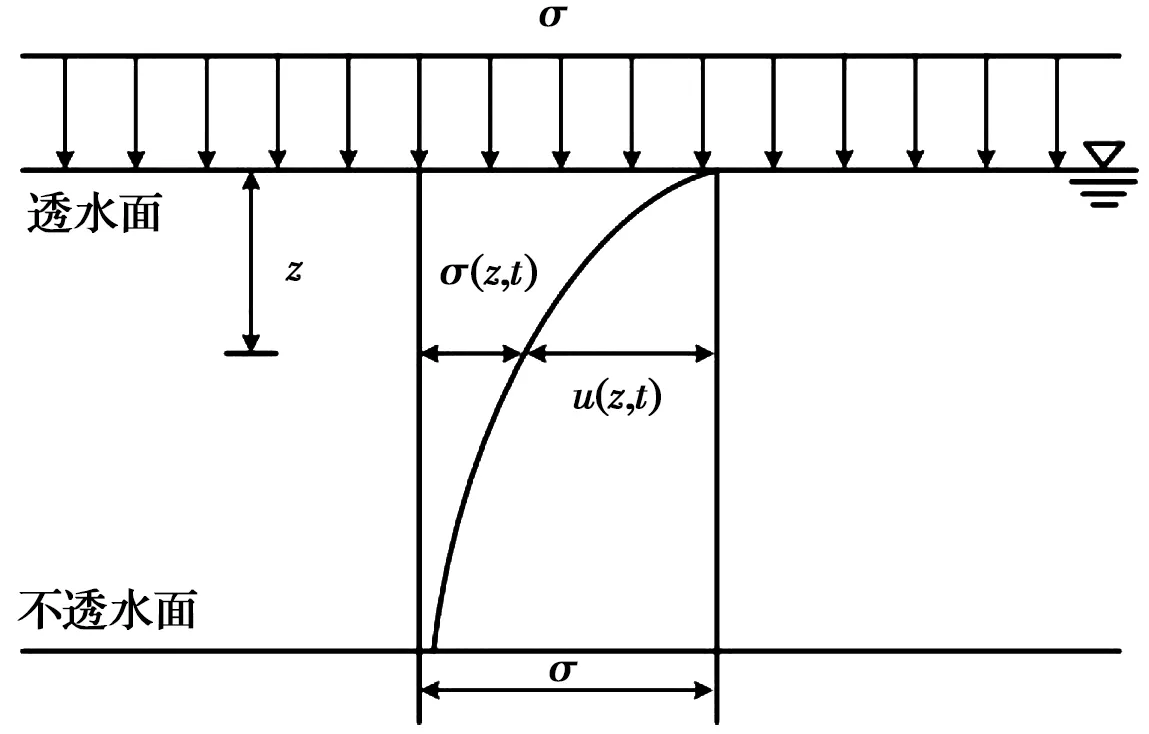
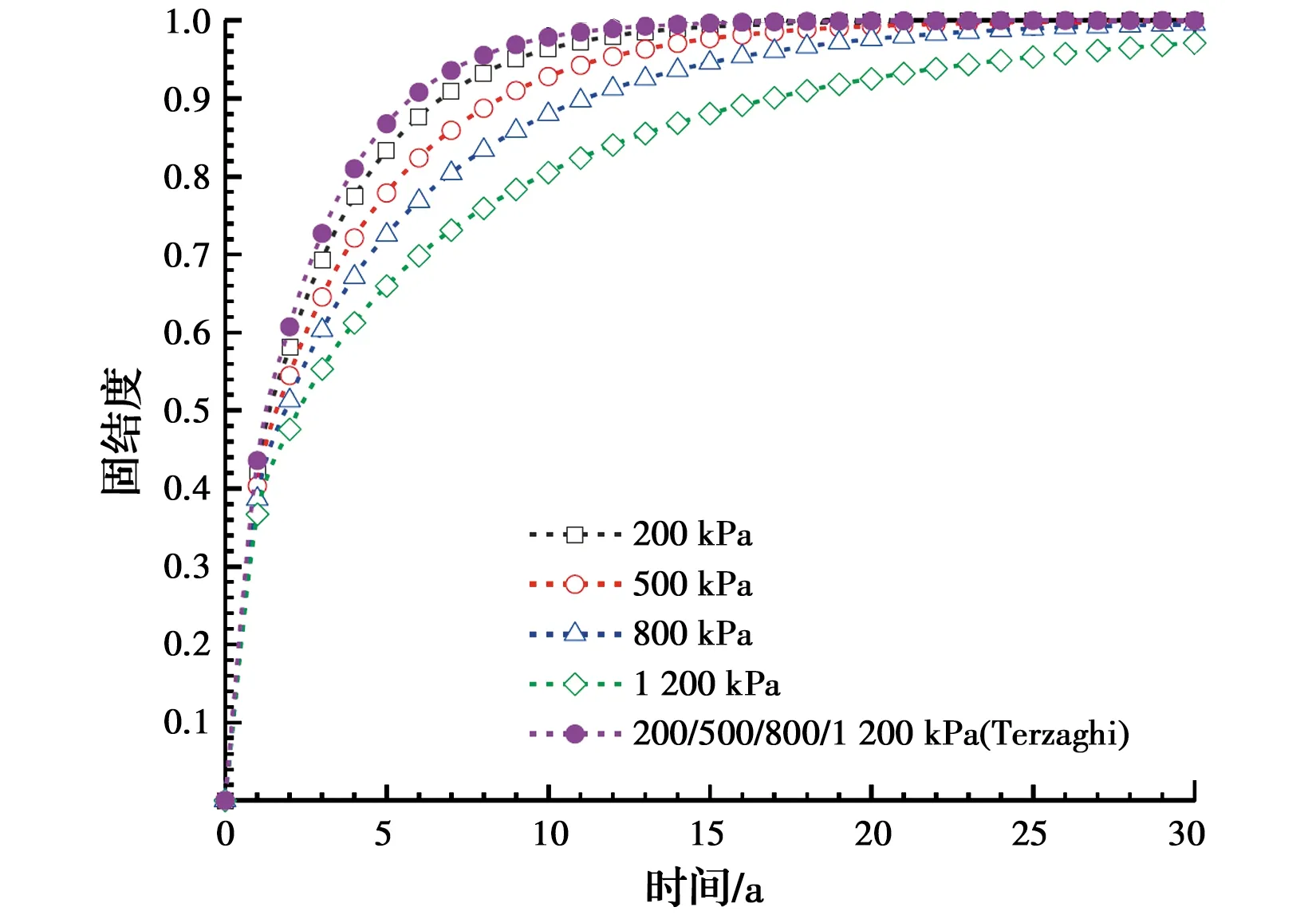
0

0

t=∞、z=H时，u=0

将对应的修正渗透系数公式代入式(31)、式(32)，采用分离变量法便可得一维固结计算公式，例如：基于柯森-卡门渗透系数预测公式的正常固结土一维固结计算公式

(33)

(34)

(35)

式中：uz为深度z处的孔压(z=1,3,5,7…)。

由此发现，无穷级数式(34)其实是一个关于(Ut,t)的隐函式，因此，可对其进行求解。采用Matlab对式(33)～式(35)及其他基于不同预测公式的一维固结公式进行编程求解，从而得到某一时间t修正后的固结度，最后把固结度代入对应的孔压公式和渗透系数公式中，便可以得到修正后某一时刻t的孔隙水压uz和渗透系数kt的预测值。在同时考虑了固结状态和固结应力的基础上，修正后的一维固结计算公式还考虑了渗透系数随时间变化的过程，更加符合土的实际固结过程，为预测地基固结提供了一种更为精确的计算方法。

3 适用性和准确性研究

利用高俊等[14]和张乐等[15]的试验数据，对预测公式的适用性和准确性进行讨论。

3.1 算例1

采用高俊等[14]的试验数据，试验土样来源于宁夏引黄灌区东干渠沙壤土，初始孔隙比e0=0.76，初始渗透系数k0=12.56×10-5cm/s，压缩指数Cc=0.19，前期固结应力75 kPa，正常固结土(OCR=1)。在试样饱和后，各级固结压力值分别为25、50、100、200、400、800、1 200 kPa，每级加载时间为t=24 h，试样高度H=4 cm，单面排水。

图4为采用式(19)～式(23)渗透系数公式计算结果与高俊等[14]的试验数据的对比。结果表明，基于中国水利水电科学研究院渗透系数修正公式的预估值与高俊等[14]的试验数据最为吻合。因此，对于预测沙壤土的固结，使用基于中国水利水电科学研究院渗透系数的修正公式更适合，计算结果更准确。

图4 渗透系数与固结应力的关系曲线Fig.4 Relation curve between permeability coefficient

3.2 算例2

采用张乐等[15]的试验数据，试验土样为陕西洛川Q3黄土，取土深度为7～8 m(粉质黏土)。初始孔隙比e0=0.93，初始渗透系数k0=1.25×10-5cm/s，压缩指数Cc=0.89，前期固结应力115 kPa，正常固结土(OCR=1)。在试样饱和后，利用GDS高级加载模块对正常固结土进行固结应力为140、165、190、215 kPa下的固结试验，每级加载总时长为t=24 h，试样高度H=8 cm，双面排水。

图5 渗透系数与固结应力的关系曲线Fig.5 Relation curve between permeability coefficient

图5为采用式(19)～式(23)渗透系数公式计算结果与张乐等[15]试验数据的对比。结果表明，基于柯森-卡门渗透系数修正公式的预估值与张乐等[15]的试验数据最为接近。因此，对于预测粉质黏土的固结，使用基于柯森-卡门渗透系数的修正公式更适合，计算结果更准确。

4 工程应用案例分析

公路路基为10 m厚的粉质黏土层，初始孔隙比为0.8，初始渗透系数为2 cm/a，压缩系数为2.5×10-4kPa-1，先期固结应力为110 kPa。采用堆载压实固结法，假定上覆均布荷载为200、500、800、1 200 kPa，如图6所示，利用修正前后的Terzaghi一维固结理论，讨论修正前后的Terzaghi一维固结方程预测的路基固结度、沉降及孔压的异同，最后与高俊等[14]、张乐等[15-16]不考虑时间的固结方程计算结果进行对比。

图6 计算模型示意图Fig.6 Schematic diagram of calculation

4.1 修正前后的Terzaghi一维固结理论对比

图7为在上覆均布荷载为200、500、800、1 200 kPa时，修正前后的Terzaghi一维固结方程预测的路基固结度Ut-t关系曲线。由图7可以发现，经典Terzaghi一维固结方程无法考虑固结应力，即上覆均布荷载为200、500、800、1 200 kPa所对应的Ut-t关系曲线相同。显然，这与实际工程情况不符，往往上覆荷载越大，所需固结时间越长，因为上覆荷载越大，孔隙比e会随着固结时间的推移变得越来越小，渗透系数也会越来越小，导致排水越来越困难，因此，需要更长的固结时间。这刚好与修正后的Terzaghi一维固结方程预测的Ut-t关系曲线一致。当固结度达到80%时，上覆均布荷载200、500、800、1 200 kPa所对应的时间t分别为4.56、5.52、6.12、9.23 a。而经典Terzaghi一维固结方程却无法考虑固结应力的影响。

图7 固结度与时间的关系曲线Fig.7 Relation curve between consolidation degree and

图8为在上覆均布荷载为200、500、800、1 200 kPa时，修正前后的Terzaghi一维固结方程预测的路基沉降St-t关系曲线。可以发现，最终的沉降值随着上覆荷载的增大而增大，分别是0.278、0.694、1.111、1.666 m。同时也发现，当上覆均布荷载较小(200 kPa)时，修正前后的St-t关系曲线较为一致，但当上覆均布荷载较大时(1 200 kPa)，修正前后的St-t关系曲线有着明显差异，修正后的Terzaghi一维固结方程预测的沉降值需要更长的时间达到稳定。其原因是孔隙比e和渗透系数kt受到上覆均布荷载的影响，即固结应力的影响，荷载越大，需要趋于稳定的时间也越长。

图8 沉降与时间的关系曲线Fig.8 Relationship curve between settlement and

图9为在上覆均布荷载为200、500、800以及1 200 kPa时，修正前后的Terzaghi一维固结方程预测的路基深度z=5 m处超孔隙水压uz-t关系曲线。可以发现，在固结初期，由于孔隙比和渗透系数比较大，孔隙水压消散得较快，随着时间的推移，土体逐渐被压缩，孔隙比和渗透系数变小，孔隙水压消散也逐渐平缓。同时也发现，当上覆均布荷载较小时(小于500 kPa)，修正前后的ut-t关系曲线较为一致，但当上覆均布荷载较大时(大于500 kPa)，修正前后的ut-t关系曲线有着明显差异，修正后的Terzaghi一维固结方程预测的孔隙水压需要更长的时间消散。

图9 孔压与时间的关系曲线Fig.9 Relationship curve between pore pressure and

4.2 一维修正固结理论对比

将Terzaghi、高俊等[14]、张乐等[15-16]和修正的一维固结方程在上覆均布荷载为1 200 kPa时的固结度Ut-t、沉降St-t及孔压ut-t的关系曲线进行对比，如图10所示。可以发现，虽然高俊等[14]、张乐等[15-16]的固结方程和修正一维固结方程的计算结果都滞后于Terzaghi一维固结方程，但高俊等[14]、张乐等[15-16]的固结方程需要更长的时间趋于稳定。其原因是高俊等[14]、张乐等[15-16]忽略了孔隙比e和渗透系数k与时间的相关性，认为其仅仅与固结状态和固结应力有关，导致孔隙比e和渗透系数k的预测值偏小，进而需要更长的时间完成固结，低估了固结速率。在实际工程中，对于固结速率的预估偏小，将不可避免地给施工过程和后期使用带来风险。因此，在预估路基固结沉降速率时，时间是不可忽视的因素之一，尤其是在上覆荷载较大、孔隙比变化较大时。

图10 一维固结理论对比关系曲线Fig.10 Comparison curve of one-dimensional

综上所述，若上覆荷载较小时，经典Terzaghi一维固结方程依然有效，可以忽略固结系数Cv的变化对固结度、沉降及孔压的影响；但当上覆荷载较大时，则不能忽视固结系数Cv的变化，同时还需要考虑时间的变化。修正后的Terzaghi一维固结方程，同时考虑了固结状态、固结应力及孔隙比变化的影响，因此，修正后的Terzaghi一维固结方程能更真实地反映固结过程，为预测地基固结提供了一种更为精确的计算方法。

5 结论

1)基于工程常用的5种渗透系数预测模型，结合固结度和侧限压缩量的关系，推导出孔隙比et的时间函数，构建了渗透系数与时间及固结应力依赖的计算公式。将所构建的渗透系数计算式代入固结系数Cv中，同时考虑固结状态、固结应力及时间的影响，对经典Terzaghi一维固结理论进行修正。

2)利用已有的试验数据，验证了预测公式的准确性。推荐基于中国水利水电科学研究院渗透系数的修正公式去预测正常固结沙壤土的固结，以及采用基于柯森-卡门渗透系数的修正公式去预估正常固结粉质黏土的固结过程。

3)修正后的Terzaghi一维固结方程同时考虑了渗透系数随时间变化及固结应力对固结系数Cv的影响，因此，能更加真实地反映固结过程。案例分析表明，若上覆荷载较小时(小于500 kPa)，经典Terzaghi一维固结方程依然有效，可以忽略固结系数Cv的变化对固结度、沉降及孔压的影响；但当上覆荷载较大时(大于500 kPa)，则不能忽视固结系数Cv的变化，另外，在与不考虑时间的固结方程对比时，发现在上覆荷载较大时，时间是不可忽视的因素之一。因此，修正后的Terzaghi一维固结方程更符合工程实际。