基于非平稳随机场的水泥土堤坝边坡可靠度分析
2022-06-21杨亮刘辉章荣军郑俊杰
杨亮,刘辉,章荣军,郑俊杰
(华中科技大学 岩土与地下工程研究所,武汉 430074)
为了处置大量的河湖疏浚淤泥,一种理想的做法是采用水泥固化高含水率泥浆,再结合真空预压、堆载预压等多种方式将水泥土作为工程(如堤坝)填料,但由于疏浚淤泥杂质众多、施工过程中搅拌不匀、养护条件不一等多种因素,疏浚淤泥固化处理后形成的水泥土堤坝边坡材料参数分布存在较大变异性[1-3]。
在固化淤泥堤坝填筑过程中,常采用真空预压加速土体固结,需要在堤坝土体内铺设多层水平排水板,针对这种条件下堤坝土体内抗剪强度的分布规律,学者们已开展相关试验研究。周洋等[4]通过试验发现,仅铺设水平排水板时,垂直于水平排水板方向,距离越远土体含水率越高,并且从土体含水率分布情况来看,仅铺设水平排水板的效果要优于仅铺设竖向排水板的效果;张文彬等[5]发现,随着离排水板距离的增加,土体的十字板抗剪强度逐渐减小;高会强[6]发现,铺设水平排水板时,加固后土体表层和靠近排水板的土体强度较高,而远离排水板的土体强度很低,铺设竖向排水板时,随着深度的增加,十字板抗剪强度呈线性增加趋势。根据已有的试验结果可知,在堤坝内铺设水平排水板会使土体的强度特性分布受到影响,且一般的规律是:在一定范围内,距离排水板越远,含水率越高,土体强度越低[7]。
为了描述土体参数的空间分布变异性并进行可靠度分析,常采用平稳随机场模型[8-9]。所谓平稳随机场即认为土体参数的均值、标准差等统计特征沿埋深保持不变,参数之间的空间相关性只与两点之间的相对距离相关而与其绝对距离无关[2]。这种模型很难表征排水板固结带来的土体强度空间变化趋势。相对于平稳随机场,也有学者提出了非平稳随机场分析模型,在非平稳随机场的表征过程中,土体参数离散变量一般可视为趋势项、残余项与波动分量的多项式,以此表征土体参数在水平方向上的波动性和埋深方向上的趋势性,许多学者展开了相关研究,提出了非平稳随机场的表征方法与趋势项及残余项的处理方法。蒋水华等[10]综合分析了两种非平稳随机场模型的特征:1)采取去趋势分析方法,将土体参数模拟为某一平稳随机场,再基于该平稳随机场,进一步考虑土体参数随埋深的变化趋势分量的影响,从而实现对土体参数二维非平稳随机场的表征[11],该方法所得非平稳随机场的均值与标准差均随埋深而变化,但其变异系数保持不变;2)取趋势项为趋势分量与土体重度和埋深的乘积,残余项为地表处土体参数值,继而将趋势分量参数模拟为服从某一分布的平稳随机场,忽略残余项的不确定性,得到二维非平稳随机场[12],该方法所得土体参数的均值、标准差与变异系数均随埋深而变化;在此基础上,Li等[13]提出了一种新的二维非平稳随机场表征方法,验证了所提方法的可行性,系统比较了所提方法与现有二维非平稳随机场与随机场的区别,该方法的优势在于能够同时考虑趋势分量与波动分量的不确定性。豆红强等[14]通过去趋势分析方法,将饱和渗透系数均值视为随埋深递减的线性函数,残余项为地表处平均饱和渗透系数,趋势分量为饱和渗透系数随埋深的变化梯度,建立了表征土体饱和渗透系数变异性的一维非平稳随机场模型,并探讨了土体饱和渗透系数的空间变异性对边坡可靠度的影响。Li等[15]通过不排水抗剪强度、有效竖向应力和黏土超固结比(OCR)之间的经验关系,研究了不排水剪切强度随埋深的变化趋势,在此基础上得到了趋势项随埋深变化的二维非平稳随机场。Shu等[16]取残余项为泥水分界线处的不排水剪切强度,取趋势项为埋深的线性函数,且趋势项与残余项满足对数正态分布,建立了不排水剪切强度的二维非平稳随机场,讨论了自相关距离对深海基础平均承载力与破坏机理的影响;Wu等[17]取趋势项为地表处非零且随埋深线性变化的不排水剪切强度均值,保持变异系数不变,通过高斯平稳随机场的转换与映射,得到了不排水剪切强度的二维非平稳随机场表征,研究了变异系数、分布函数、垂直自相关距离等因素对土体承载力的影响。
基于上述垂直排水板方向强度衰减的一般规律及非平稳随机场相关理论,笔者提出一种水泥土堤坝内垂直排水板方向的不排水抗剪强度随距离衰减的非平稳随机场模型,该模型既能表征土体抗剪强度沿埋深方向增加的趋势,又能考虑垂直排水板方向的强度衰减。在此基础上,给出土体参数三维非平稳随机场模拟计算方法流程,并分析了土体参数非平稳分布特征对边坡可靠度的影响。
1 不排水抗剪强度非平稳随机场模型
1.1 深度趋势随机场
土体参数的空间变异性一般由趋势项和随机波动项联合表征。以无侧限抗压强度随机场为例,试验值qu沿深度方向的不平稳特征可表示为
qu(h)=t(h)+ω
(1)
式中:h为土体埋深;t(h)为与埋深有关的趋势项,一般取相应深度下土体参数的均值;ω为随机波动项,用来描述土体空间内土体参数大小无趋势的随机波动特征,其均值和标准差与埋深无关。通常,土体的无侧限抗压强度随深度增加而增加。简单起见,用线性函数描述土体无侧限抗压强度随深度的变化关系[10],即
qu=qu0+b1·σv′=qu0+γ·h·b1
(2)
式中:qu0为地表土体的无侧限抗压强度(地表UCT试验值);b1为无侧限抗压强度随埋深增加的速率;σv′=γh,为竖向有效应力,γ为土体重度。参考文献[10]的做法,采用去趋势分析方法,首先用一均值为μqu0、标准差为σqu0的对数正态平稳随机场模拟qu0,再在此基础上叠加一个沿埋深线性增加的趋势分量,最终得到三维深度趋势非平稳随机场
qu=qu0(x,y,z)+γ·h·b1
(3)
1.2 垂直排水板不排水抗剪强度衰减非平稳随机场模型
基于已有的试验研究[4-7],可假设土体在排水固结后,抗剪强度与其离排水板的距离线性相关,此时土体随机场可表示为
qu(x,y,z)=qu0+γ·h·b1-d(x,z)·
b2·exp[ω(x,y,z)]
(4)
式中:qu0、b1的含义同前所述,只是此处qu0为均值,为μqu0、标准差为σqu0的随机变量;d(x,z)为土体空间内一点与排水板的垂直距离(排水板沿y方向铺设);b2为垂直排水板方向的趋势项;exp[ω(x,y,z)]为随机波动项。
如图1所示,P为三维空间中截取的某一x-z平面内一点,因排水板(铺设)方向平行于y轴方向,故点P垂直排水板距离d(指距离最近的排水板)只与点P的x、z坐标有关,而与x-z平面所处的位置(y坐标)无关,表示为d(x,z)。
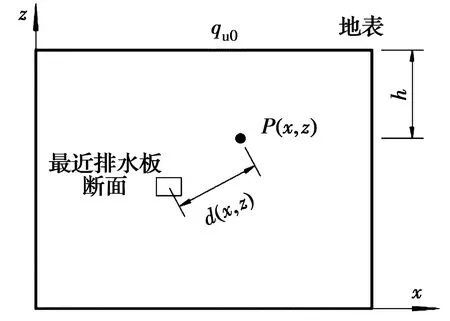
图1 与排水板的垂直距离d(x,z)Fig.1 Distance d(x,z) along the normal direction
2 算例分析
2.1 算例描述
算例为一高陡水泥土堤坝边坡,斜坡高度6 m,坡度1∶0.5,堤坝顶面宽度为18 m,堤坝顶面作用20 kPa的交通荷载(假设为均匀分布)。为了提高计算效率,取半结构进行建模分析,模型断面图和三维网格图如图2所示。
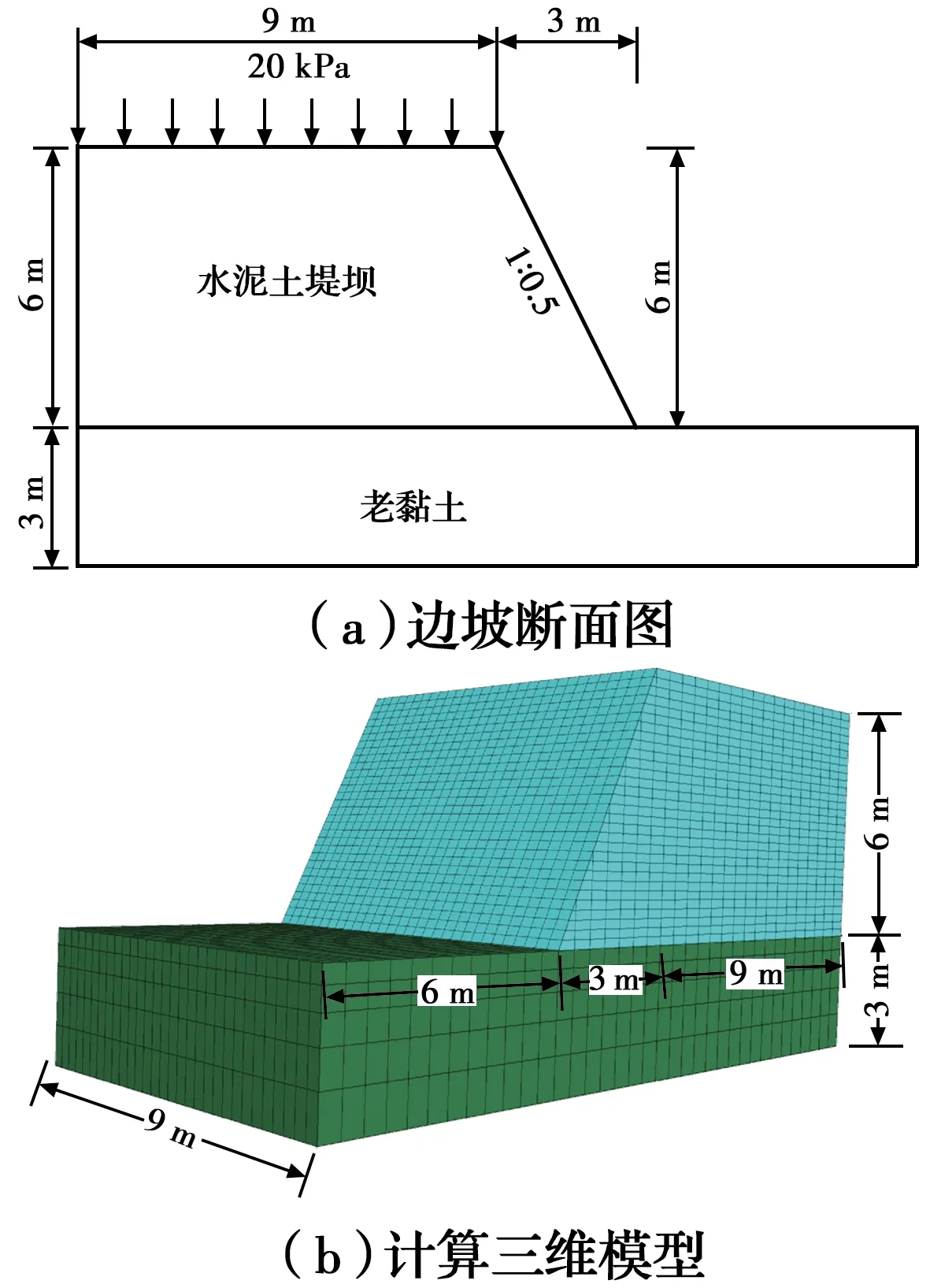
图2 边坡断面图及三维网格模型Fig.2 Slope profile and mesh grid for numerical
2.2 材料参数取值
参照Zhang等[18]、Lee等[19]的研究,认为水泥土堤坝边坡无侧限抗压强度服从对数正态分布,固化淤泥形成的水泥土模量E与无侧限抗压强度qu呈正比关系,E/qu=135~140。考虑到固化淤泥形成的水泥土材料渗透系数很低,参考Liu等[20]的做法,假定主固结完成后水泥土堤坝为完全不排水条件,采用内摩擦角为0的Mohr-Coulomb模型来模拟固化淤泥形成的水泥土,取不排水抗剪强度cu=qu/2、E/qu=140。相应地,堤坝地基土体为老黏土,相关材料参数见表1。

表1 土体材料参数
为了探究垂直排水板衰减非平稳随机场模型的可行性,采用3种随机场模型模拟水泥土堤坝部分对比计算结果,下部老黏土采用一般的平稳随机场模型。
模型1为平稳随机场模型,采用地表处的UCT试验均值μqu0=86 kPa,不考虑其趋势变化,UCT试验值空间随机场采用对数正态分布,变异系数COV=0.3。采用高斯型自相关函数,三维空间内水平、竖向相关距离分别取为38、3.8 m。
模型2为深度趋势随机场模型,三维空间随机场生成公式为
qu(x,y,z)=qu0(x,y,z)+γ·(6-z)·b1
(5)
式中:qu0(x,y,z)为对数正态分布的平稳随机场,离散取值同上。土体趋势分量参数b1随深度变化,参照蒋水华[10]的统计结果,取b1=0.2,为定值。不排水抗剪强度的均值和标准差分别为
(6)
模型3为垂直排水板衰减非平稳随机场模型,在模型计算时,认为排水板附近土体的抗剪强度不断减小。同时,采用静力计算,不考虑排水带来的渗透固结作用,也不考虑排水板自身对土体强度分布的影响。此时,三维空间随机场生成模型为
qu(x,y,z)=qu0+γ·(6-z)·b1-
d(x,z)·b2·exp[w(x,y,z)]
(7)
式中:qu0为对数正态分布的随机变量,μqu0=86 kPa,变异系数COV=0.3;趋势参数b1=0.2,为定值;b2为因真空预压排水固结导致的qu随距排水板距离衰减趋势项(排水板处最大),理论上与施工条件有关,参考b1的取值结果,考虑其随机性,取b2为对数正态分布的随机变量,均值μb2=2.0,变异系数COV=0.3;exp[w(x,y,z)]为随机波动项,w(x,y,z)取为均值μw=0、标准差σw=0.3的正态分布随机场,水平、竖向相关距离分别取38、3.8 m。不排水抗剪强度的均值和标准差分别为
2.3 水泥土堤坝边坡可靠度计算分析流程
采用Karhunen-Loeve级数展开法离散随机场,每一工况生成500次随机场,结合蒙特卡洛模拟和强度折减法分析堤坝边坡失效概率,主要分析计算流程如图3所示,其中,强度折减法将边坡安全系数定义为使边坡刚好达到临界破坏状态时对其强度的折减程度[21]。采用Mohr-Coulomb破坏准则时,其折减的强度参数是黏聚力c和内摩擦角φ(对于本例的不排水条件,仅折减黏聚力c),一般通过二分法迭代计算,通过不断扩大(或缩小)折减值,直至折减系数的上下限满足精度要求,将安全系数Fs定义为初始黏聚力ci和破坏时的黏聚力ccr之比,即Fs=ci/ccr。
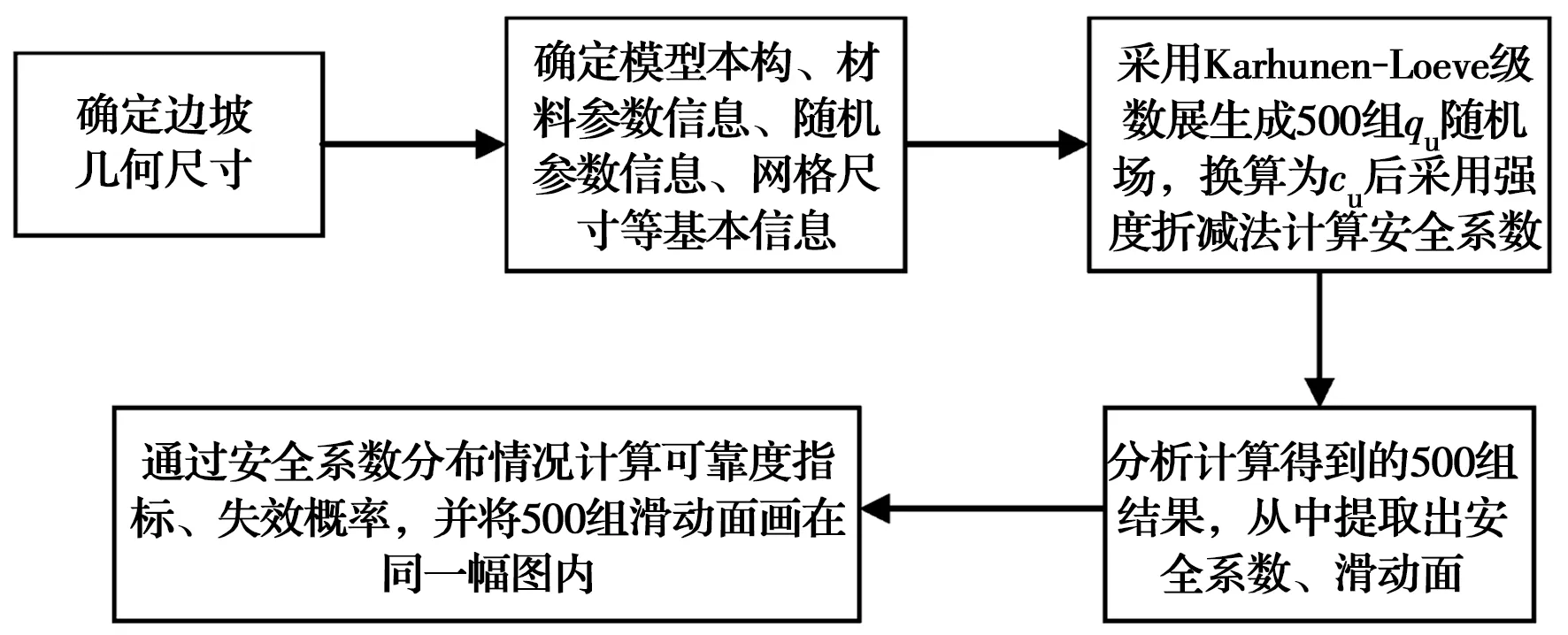
图3 基于蒙特卡罗方法的边坡可靠性分析Fig.3 Analysis of slope reliability based on
随后统计一个工况内500组随机场模型计算结果,可得到安全系数的分布,并借此计算可靠指标、失效概率。
若安全系数的分布呈正态分布,则可靠指标
(9)
当安全系数呈对数正态分布时
(10)
式中:β为可靠指标;μFs为500组安全系数均值;σFs为500组安全系数标准差,VFs=σFs/μFs。利用可靠指标β与失效概率Pf之间的数学关系,可以用式(11)计算出可靠指标。
Pf=1-Φ(β)
(11)
3 3种随机场模型对比
3.1 3种随机场模型实现情况对比
图4为3个模型堤坝土部分同一竖线上(参考图5(a)、(b),y=0平面上、x=3.6 m这条线)不同

图4 cu沿土体埋深方向的5次统计值Fig.4 Five typical realizations of random field of undrained
cu的统计值(cu=qu/2)。可以看出,对于模型1,cu大小随深度并无明显增加趋势,但沿深度呈现出随机波动趋势,且波动幅度较大。模型2呈现出cu均值随深度增加的趋势,能够在一定程度上表征土体的非平稳特征。
模型3则表现出了沿深度增加和周期性波动的趋势,波动幅度明显小于模型1和模型2。这种周期性波动的原因是:土体不排水抗剪强度cu沿深度方向有增加的趋势,但由于排水板加速局部的排水固结,使得局部强度最高,局部强度最大值即为排水板铺设位置,远离排水板则强度减小。这一效果与前述试验规律基本一致,且随着深度的增加,波动幅度增大,说明模型3的cu均值沿深度方向增加。
图5为模型3三维网格不排水抗剪强度cu分布结果,采用局部平均方法得到,图5(b)、(c)分别为三维模型的两方向上的断面,排水板铺设方向平行于边坡横截面,其横截面分布在三维边坡内的铺设点为图5(b)中的白点,可以看出,排水板四周土体的强度最高,随着离排水板距离的增加,土体强度逐渐降低,也基本符合前文所述研究规律。在平行于排水板方向,
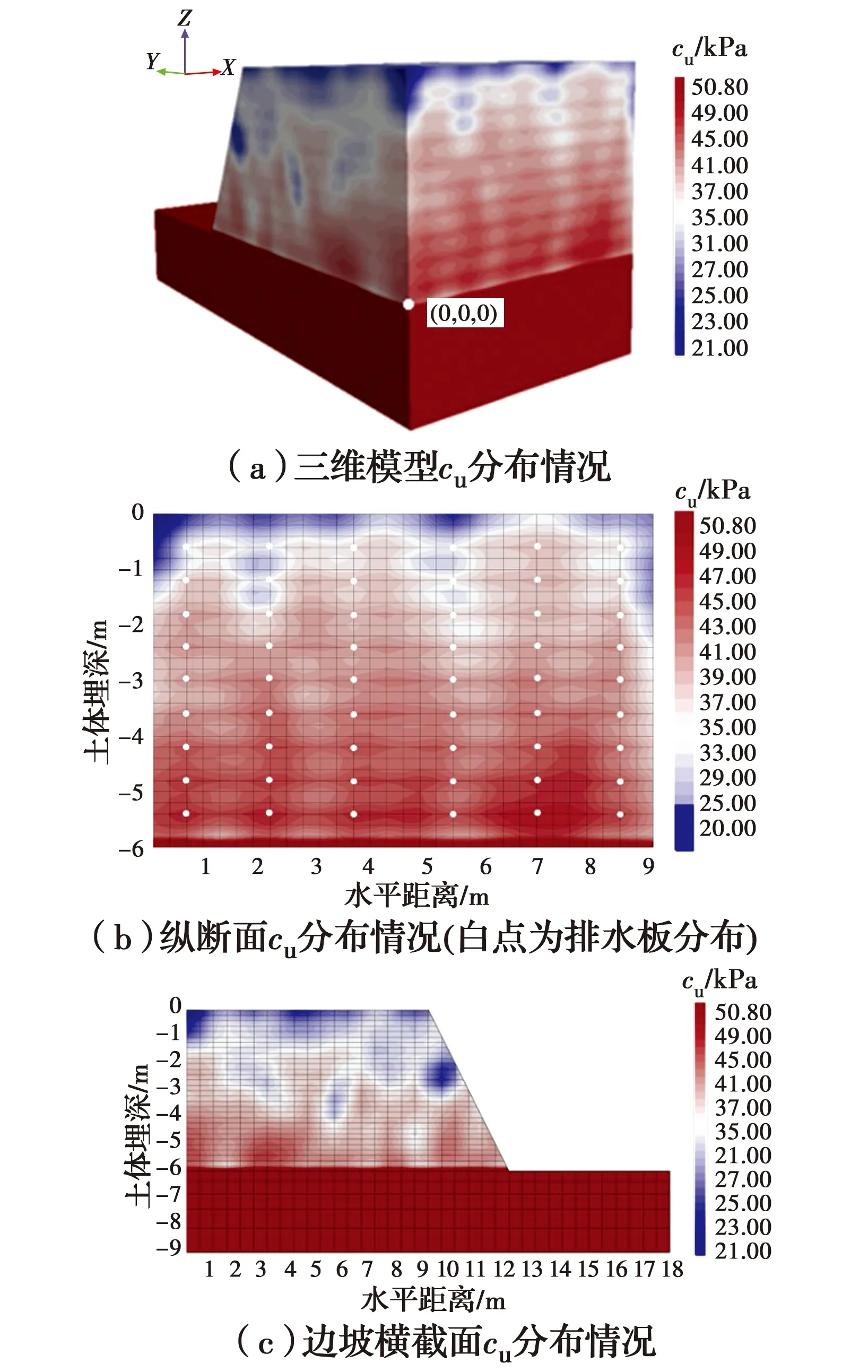
图5 模型3中cu三维空间分布情况Fig.5 Three-dimensional spatial distribution of model 3
边坡横截面上,不排水抗剪强度cu分布则近似于深度趋势随机场,在深度方向上呈增大的趋势,波动性亦很强。
3.2 3种随机场模型计算结果对比
对上述3种典型工况分别进行500组蒙特卡洛模拟,利用强度折减法得出500组安全系数,模型3的安全系数分布情况如图6所示,对分布情况进行K-S检验发现,采用对数正态分布拟合时,其p=1,说明对数正态分布符合较好。经检验,其他工况安全系数分布同样符合对数正态分布。
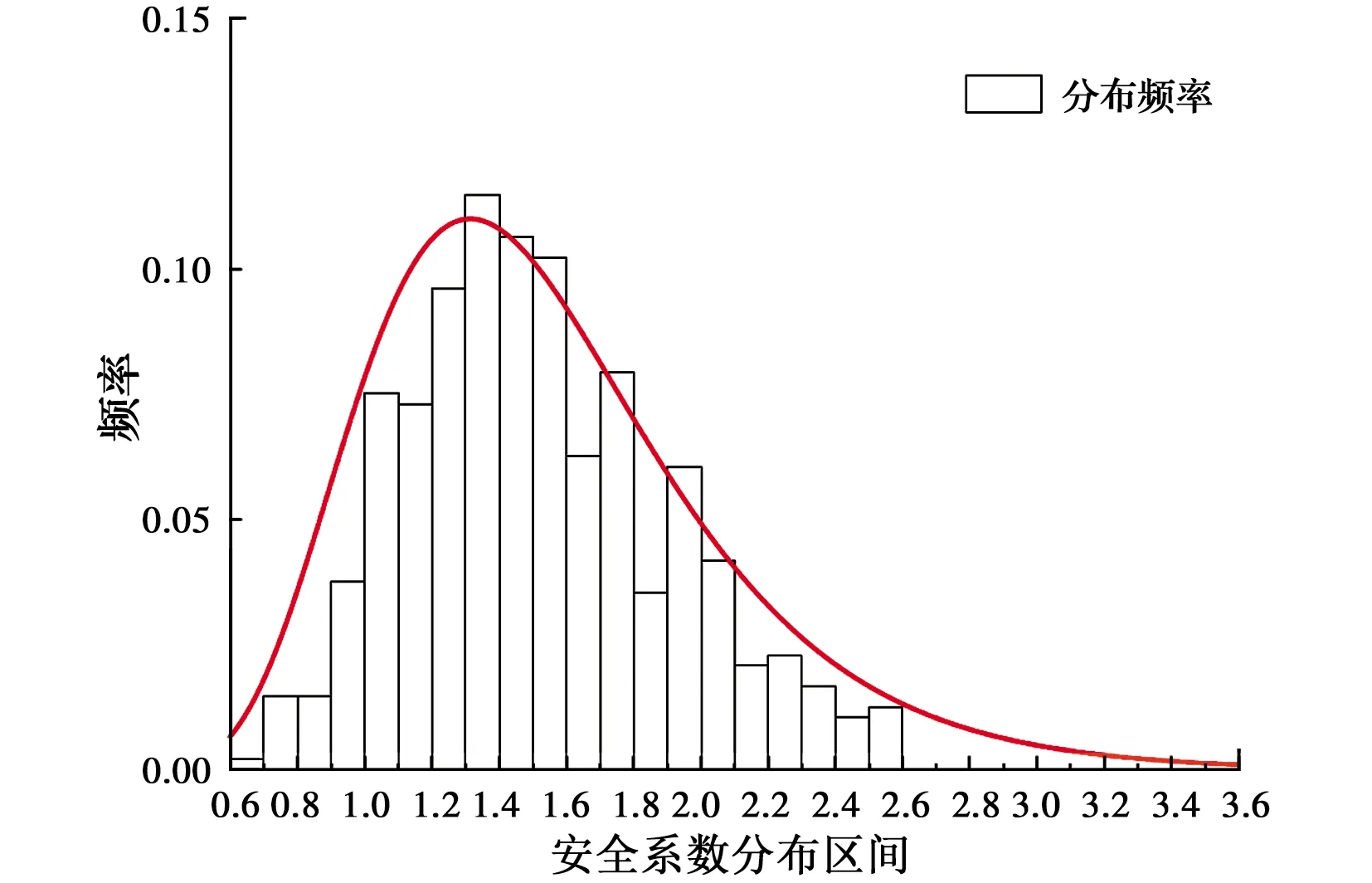
图6 模型3的安全系数分布情况Fig.6 Distribution safety factors of model
模型1、模型2、模型3分别对应的可靠指标为1.34、2.79、1.30。从式(5)可见,模型2深度趋势模型的各项均为正,强度不存在衰减,理论上是“最安全”的工况,结果也验证了这一点。
参考李剑等的做法[22],选取边坡达到极限状态时所有垂线上最大剪应变增量的位置,通过最小二乘法拟合圆弧滑动面,3种典型工况的滑动面分布结果如图7所示。3种典型工况的边坡滑动面都主要发生在水泥土堤坝土体内,但模型1、模型2的离散性更强,滑动面顶端与坡顶距离不一,滑动体体积也差距较大,模型3的滑动面则主要为从坡底贯穿坡顶的滑动面,分布集中。
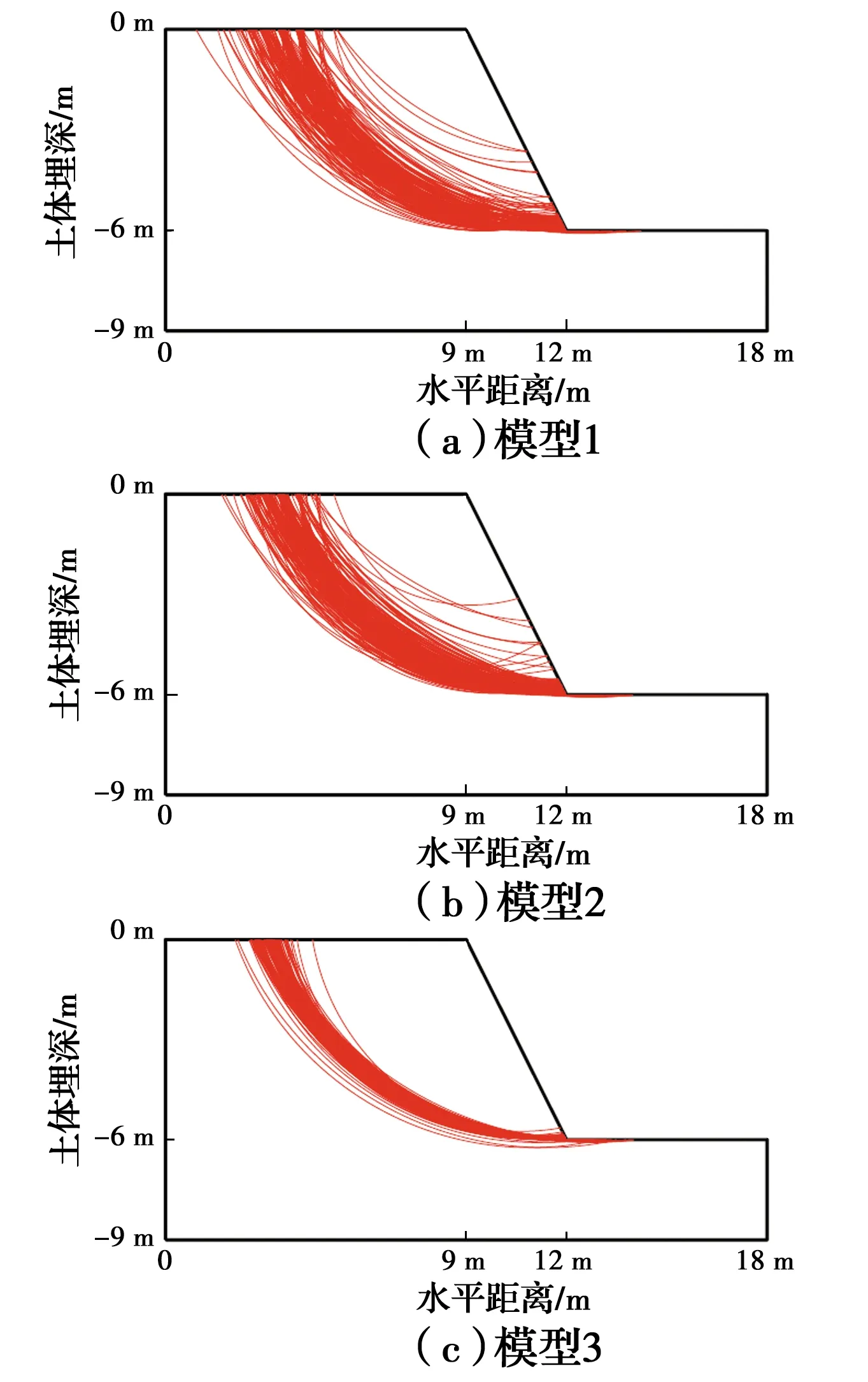
图7 3种典型工况滑动面分布情况Fig.7 Distribution of sliding surface under three
为了探究地表UCT实验值qu0的变异系数对模型结果的影响,分别对3种模型加算COV=0.2、0.4的工况,其最终结果如图8所示,随着变异系数的增加,3种模型计算得到的安全系数标准差增大,而安全系数均值变化不明显,导致可靠指标均减小。3种工况的安全系数均值μFs分别为1.39、1.70、1.55。若仅考虑安全系数均值μFs,3种工况均能满足规范[23-25]要求,但可靠度仅模型2(深度趋势)能满足,并且模型3的安全系数离散程度高,变异性强,采用确定性分析或者平稳随机场模型偏于危险,讨论模型3随机分布情况就显得更为重要。
3.3 趋势参数b2对安全系数分布的影响
为了探究模型3中趋势参数b2对安全系数分布的影响,分别单独取随机场离散公式(7)中b2均值为1、1.5、2.5,b2变异系数为0.1、0.2、0.4,其他参数保持不变,共6种工况,将其计算结果分别汇总于表2、表3,并与基础工况(b2均值为2、变异系数为0.3)对比。从表中可以看出,无论是提高b2的均值还是变异系数,最终都表现出可靠指标降低,失效概率增大的趋势。其中,b2均值的增加带来式(7)中最终强度的减小,安全系数均值μFs减小,标准差σFs增大,变异性增强;b2变异系数增大,安全系数均值μFs基本未改变,但安全系数标准差σFs增大,变异性增强。
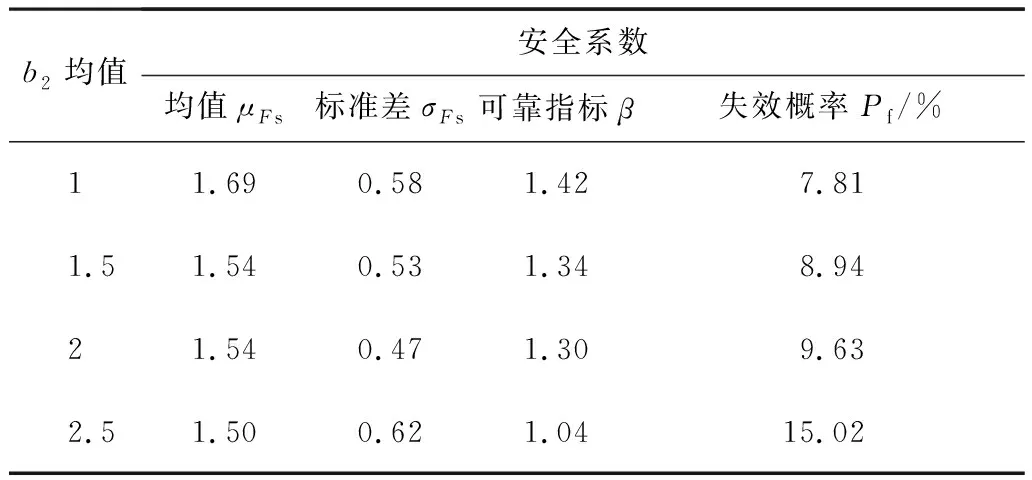
表2 趋势参数b2均值对安全系数的影响
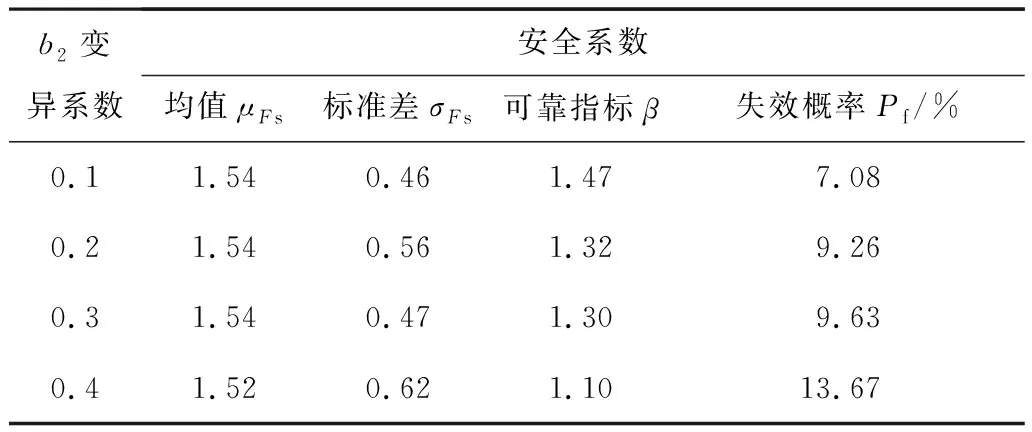
表3 趋势参数b2变异系数对安全系数的影响
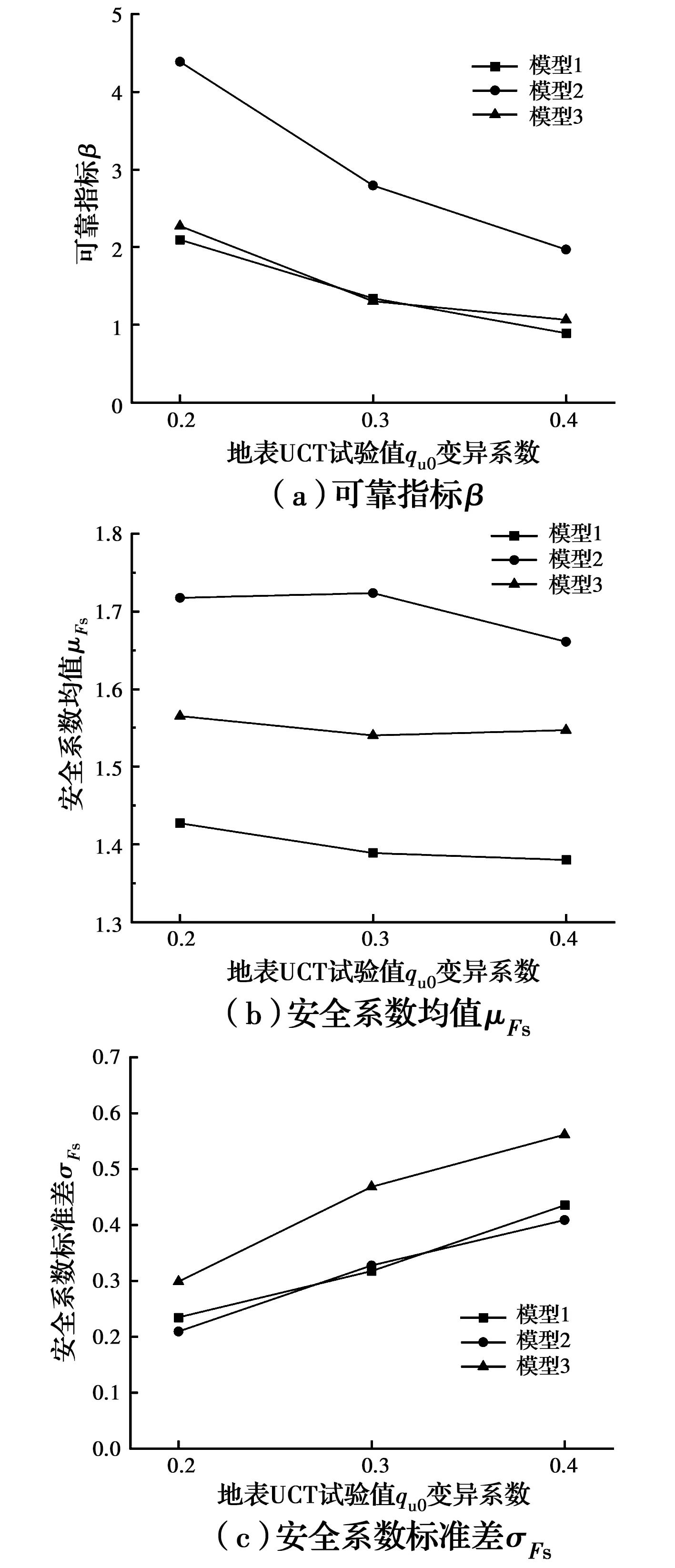
图8 3种模型的可靠指标β与安全系数分布对比Fig.8 Comparison of reliability index β and safety factor distribution among three
4 结论
结合强度折减法、蒙特卡洛模拟方法,比较了3种随机场模型对水泥土堤坝边坡的失效风险和滑动面位置的影响,得到以下结论:
1)对于水泥土边坡的可靠度分析问题,采用平稳随机场或深度趋势随机场可能会高估边坡的可靠度,使计算结果偏于危险;即便是安全系数均值满足规范要求,但其标准差过大,最终的可靠指标并不能满足工程要求。
2)提出的不排水抗剪强度垂直排水板衰减非平稳模型既能考虑沿深度方向的趋势项,又能考虑垂直排水板方向的衰减趋势,综合表现为沿深度方向的近似周期性波动,与现有研究符合较好。在该模型中,趋势参数b2对随机场模型的影响较大,当其值和标准差增加,最终都将降低计算模型的可靠指标,失效概率增大。
3)提出的不排水抗剪强度垂直排水板衰减非平稳模型的边坡破坏形式较为集中,大部分破坏面集中在堤坝土土体内,且多为从坡底贯穿坡顶的滑动面。
