赵东油田老平台T 型管节点极限承载力弱化规律研究

靳 嵩，胡杨俊，殷庆国，卫 宪

（1.中国石油大港油田分公司对外合作项目部（赵东作业分公司），天津 300280；2.中国石油大学（北京），北京 102249；3.中国石油大港油田分公司石油工程研究院，天津 300280）

赵东油田位于渤海湾浅海区域，其中一期建设的ODA（赵东A 号井口平台）和OPA（赵东A 号原油处理平台）等固定式导管架平台即将达到20年的设计使用寿命。随着平台服役年限增加，在长期服役过程中受海水腐蚀、环境荷载等作用下，导管架管节点附近将产生腐蚀和裂纹，从而严重影响海洋平台结构的力学性能，增加平台结构失效风险。在我国提倡能源保障安全的背景下，研究并掌握老平台管节点承载力弱化机理，是老油田提质增效、延长平台服役期的增效利器。

针对导管架管节点承载力预测，窦培林等[1]利用非线性分析的有限元方法对K 型和双K 型圆管相贯节点进行了数值计算；嵇春艳等[2]通过实验研究了裂纹腐蚀损伤对导管架平台极限承载力的影响；雷婷[3]研究了有焊缝下的K 型及T 型管节点承载力与几何参数之间关系。而针对裂纹、腐蚀因素对海洋结构物的极限承载力影响，PAIK J K 和王生楠等[4-6]学者对考虑结构裂纹影响下板的极限承载力做了大量的研究，对含裂纹板和加筋板结构剩余极限承载力进行了评估；张婧等[7]采用非线性有限元法开展含裂纹、点蚀损伤的加筋板在轴向压载作用下的极限承载力研究；FARZANEH A 等[8]采用非线性有限元法研究了均匀平面压缩条件下点蚀和纵向裂纹板的极限承载力；FENG L 等[9]采用非线性有限元研究，研究了耦合腐蚀和裂纹损伤对钢板及加强箱梁残余极限承载力的影响。

本文以赵东油田ODA 老平台的T 型管节点为研究对象，采用数值模拟方法研究了腐蚀坑及裂纹损伤对管节点极限承载力的弱化规律，重点分析了裂纹长度与深度、腐蚀坑位置与数量、材料腐蚀修正本构影响、裂纹与腐蚀联合作用等因素对管节点的极限承载力变化规律。

1 管节点有限元模型建立

1.1 T 型管节点尺寸参数

赵东油田ODA 平台结构的导管架如图1 所示，作为浅水区域的导管架平台其只有一层水平层[10]。从图1 中可看出该导管架平台的水平层主要由K型管节点和T 型管节点构成，以T 型管节点为主。因此，本文选择如图1（b）所示位置的T 型管节点为研究对象开展后续研究工作[11-14]。所选T 型管节点的具体结构如图2 所示，其具体几何尺寸见表1。

图1 赵东油田ODA 平台模型

图2 T 型管节点示意图

表1 模型尺寸数据

1.2 T 型管节点有限元模型

如图3 所示，本文选用ABAQUS 中的八结点线性六面体单元（C3D8R）建立T 型管节点有限元模型，为模拟管节点焊缝位置应力集中情况进行了局部网格加密。主管两端采取铰接固定（U1，2，3= 0），支管的外端除加载方向y 方向线位移不约束外，其他方向自由度均约束（U1，3= 0，ROT1，2，3= 0）。在加载过程中荷载是以面荷载的形式作用在腹杆上部的端板，将支管外端所有节点耦合到外端面的中心点处，使用耦合约束将上部端板与端板的中心点建立刚性连接，在耦合点施加轴向位移载荷。

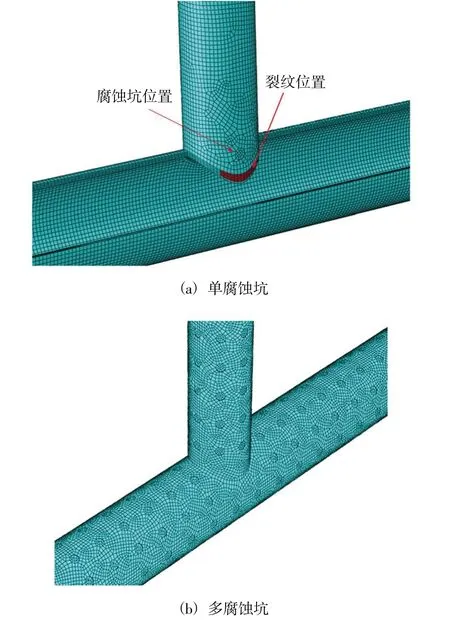
图3 T 型管节点有限元模型

荷载传递函数模型比较有代表性的有双折线模型和三折线模型[15]。三折线钢材应力—应变关系模型，如图4 所示。从图中可看出三折线模型包含弹性段、屈服段和强化段。陈明中等[16]分别对双折线模型和三折线模型进行了理论分析，指出三折线较双折线具有更高的模拟精度，能较为真实准确地反映钢材各项拉伸力学性能。

图4 三折线模型

本模型采用三折线模型，采用基于弧长控制的Newton-Raphson 方法求解。此次数值计算不考虑焊缝和残余应力对节点极限承载力的影响。

1.2.1 裂纹损伤模拟

赵东油田老平台在风浪流等往复荷载作用下，管节点构件焊缝位置萌生的疲劳裂纹通常沿焊趾扩展穿透圆管构件的管壁[17]。因此，本文将裂纹布置在模型的焊趾处，并采用内聚力粘结方法模拟裂纹损伤（cohesive 单元）。为考虑裂纹在管节点焊缝不同位置对管节点极限承载力影响，将裂纹模拟单元分别设置在如图5 所示的不同位置。

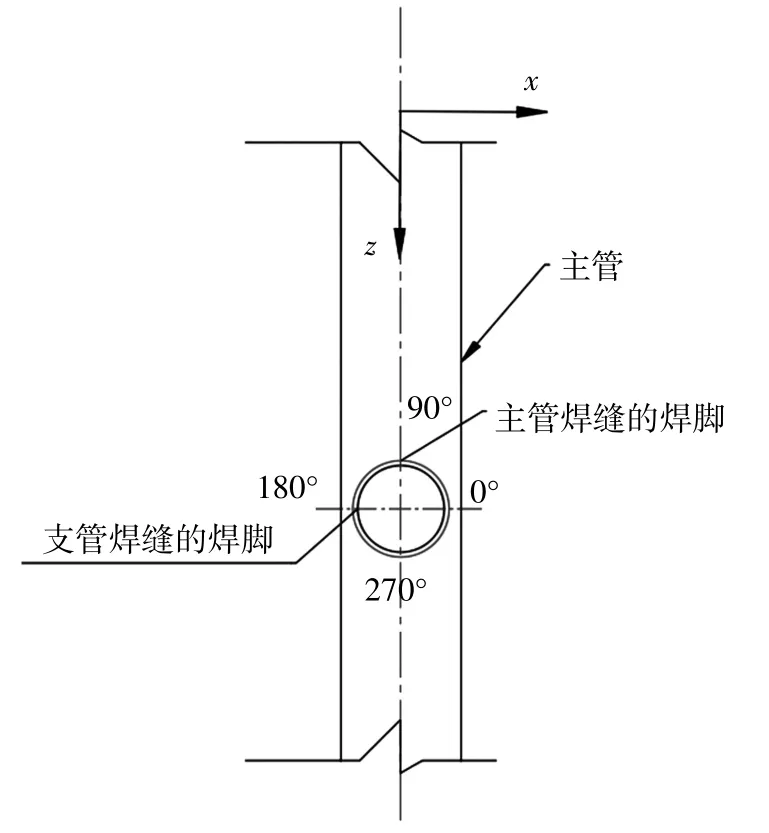
图5 裂纹布置区域示意图

1.2.2 腐蚀损伤模拟

本文针对导管架的主要腐蚀形式——局部点蚀开展模拟研究[18-20]，采用构造一个或若干个圆柱坑来模拟腐蚀坑形状，腐蚀坑距离焊缝的距离如图6所示。

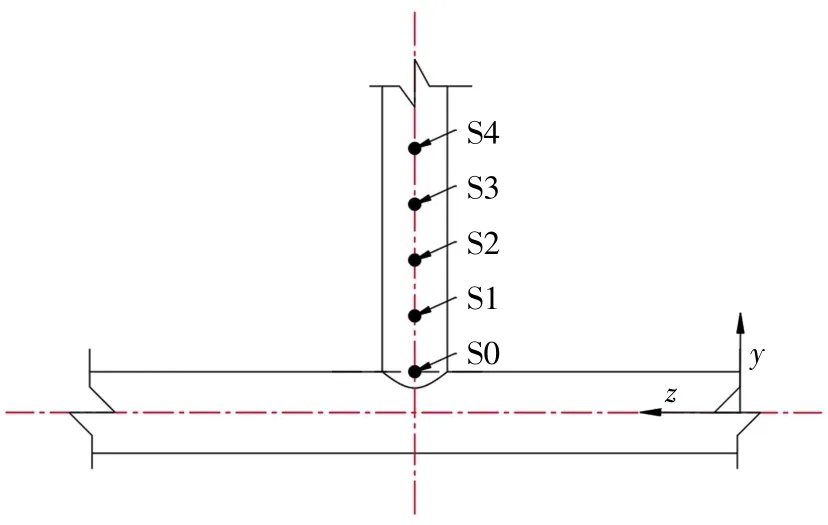
图6 腐蚀坑布置位置示意图

由于管节点腐蚀损伤不仅会减少构件的截面尺寸，还会在微观层面上影响材料的本构特性。为考虑此类腐蚀特性对管节点极限承载力影响，本研究在采用若干腐蚀坑模拟大面积腐蚀条件时，将使用考虑三折线本构模型的修正参数[21]，如表2 所示。

表2 修正后的三折线本构模型力学特征参数取值

管节点的腐蚀率计算公式如下。

式中，n 为腐蚀坑数量；r 为腐蚀坑半径；h 为腐蚀坑深度；D 为管节点直径；t 为管节点壁厚；L为管节点的长度。

将本文选取的管节点参数和腐蚀坑参数带入到腐蚀率计算公式，再将得到的腐蚀率数据代入到表2 的参数关系式，即可得到ODA 平台所选T 型管节点腐蚀修正后的钢材力学参数。本次共计算了6 种腐蚀率下修正材料数据，如表3 所示。

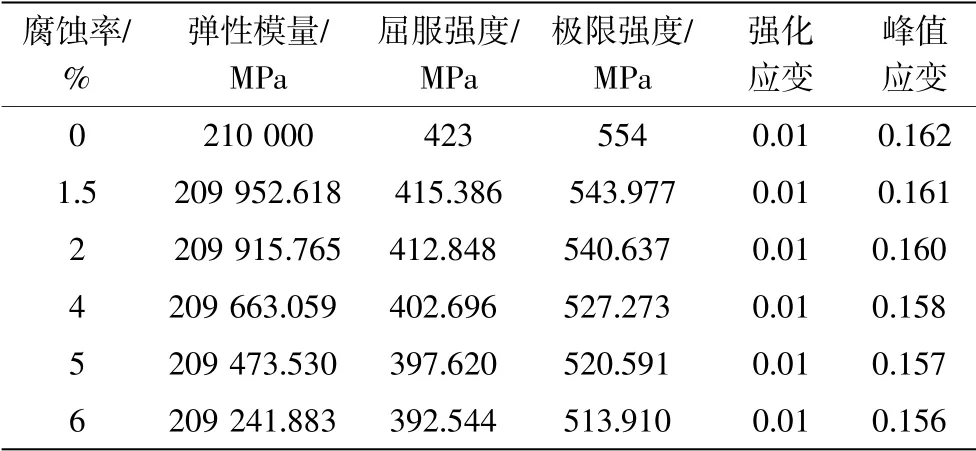
表3 修正后的材料数据

1.3 有限元模型验证

在开展数值模拟分析前，先通过与CHEN Y等[22]文中的实验数据进行对比，以验证本文采用的有限元模拟方法的正确性。实验X 节点的主管两端不做任何约束，支管两端焊接上铁片，方便固定与施加载荷，支管的一端固定在实验台上，另一端通过液压机施加向下的位移载。实验选用管节点的几何尺寸和材料属性见表4 所示。运用本文采用的模拟方法建立有限元模型后，为了贴合实验结果，本文在进行有限元模拟时，X 型节点模型的主管不施加任何约束，支管下端面按固定端约束，上端除加载方向y 方向线位移不约束外，其他方向自由度均约束。将支管上端所有节点耦合到外端面的中心点处，以模拟铁片的受载效果，在耦合点处施加轴向位移载荷。X 型节点在极限状态时实验变形图与模型变形图对比见图7，其极限承载力的结果对比见表5。

表4 X 型节点几何尺寸

从图7 可以看出，在主支管相贯区应力较大，并产生较大的塑性变形，与实验模拟的破坏模式一致，均为主管塑性的破坏模式；从表5 中X 节点的极限承载力计算结果可以看出，有限元模拟结果与实验结果的最大相对误差为1.37%，由此验证了本文采用的有限元模拟方法的准确性。

表5 极限承载力计算结果对比

图7 X 型节实验变形图与有限元模型变形图

2 各损伤参数对管节点极限承载力影响

下面针对不同裂纹及腐蚀损伤及其组合影响情况下，分别建立数值模型开展参数分析。不同损伤参数取值和所选T 型管节点的极限承载力计算结果如表6 所示。编号M 表示无裂纹无腐蚀的完好管节点模型；L0～L4 表示只含裂纹损伤，裂纹深度相同但长度不同的管节点模型；D0～D4 表示只含裂纹损伤，裂纹长度相同但深度不同的管节点模型；S0～S4 单腐蚀坑损伤管节点模型；P0～P5 表示含有若干腐蚀坑下的不同腐蚀率模型，P0 与P1 腐蚀率相同，P0不考虑本构模型修正，P1～P5 考虑本构模型修正；R0～R3 表示裂纹腐蚀联合模型，但裂纹与腐蚀的相对位置不同。

2.1 裂纹参数的影响

根据表6 中单裂纹模型L0～L4 的计算结果，在保持裂纹深度不变，改变裂纹长度的情况下，管节点极限承载力折减率比较小，通过不同裂纹长度与极限承载力关系图8 可以看出，随着裂纹的长度增加管节点的极限承载力逐渐减小，其变化比较均匀，其变化趋势呈现类线性关系。

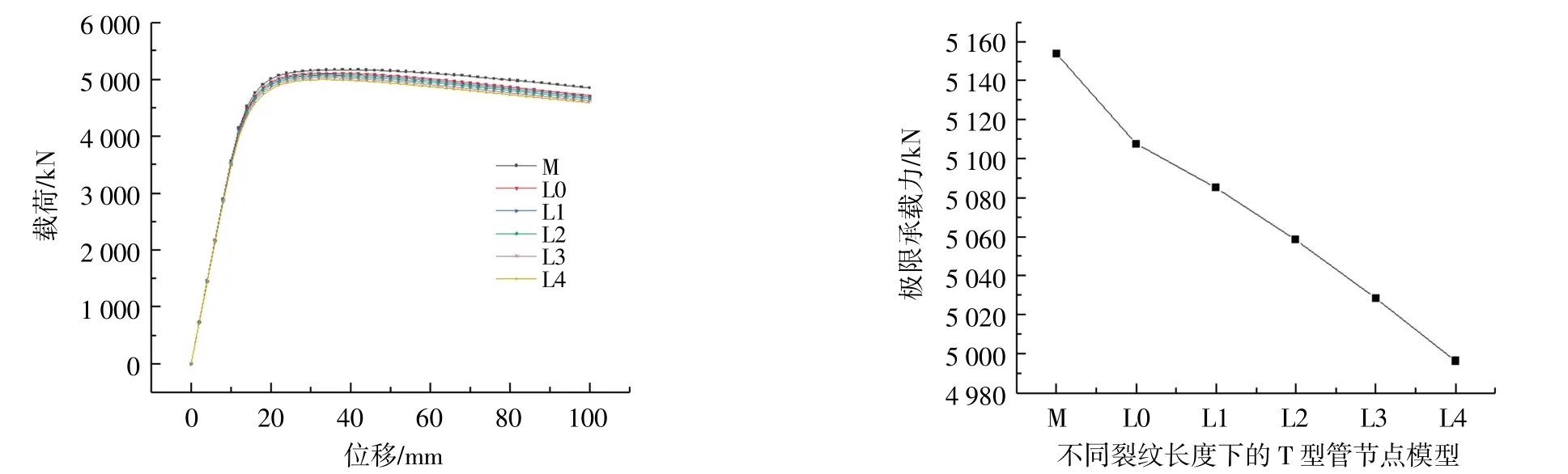
图8 不同裂纹长度的承载力曲线

表6 T 型管节点损伤参数与极限承载计算

同样在单裂纹模型D0～D4 下，保持裂纹长度不变，改变裂纹的深度。在裂纹深度达到t0前，管节点的极限承载力折减率变化较小，在裂纹深度达到t0时，极限承载力折减率达到-8.37%。从图9 中也可以看到，在裂纹未发展成贯穿裂纹前，极限承载力均匀下降，贯穿裂纹的出现导致承载力骤降。在工程实际中，结构出现裂纹时，在裂纹发展前期结构还能保证可靠性，但要及时进行修补，避免发展成为贯穿裂纹。

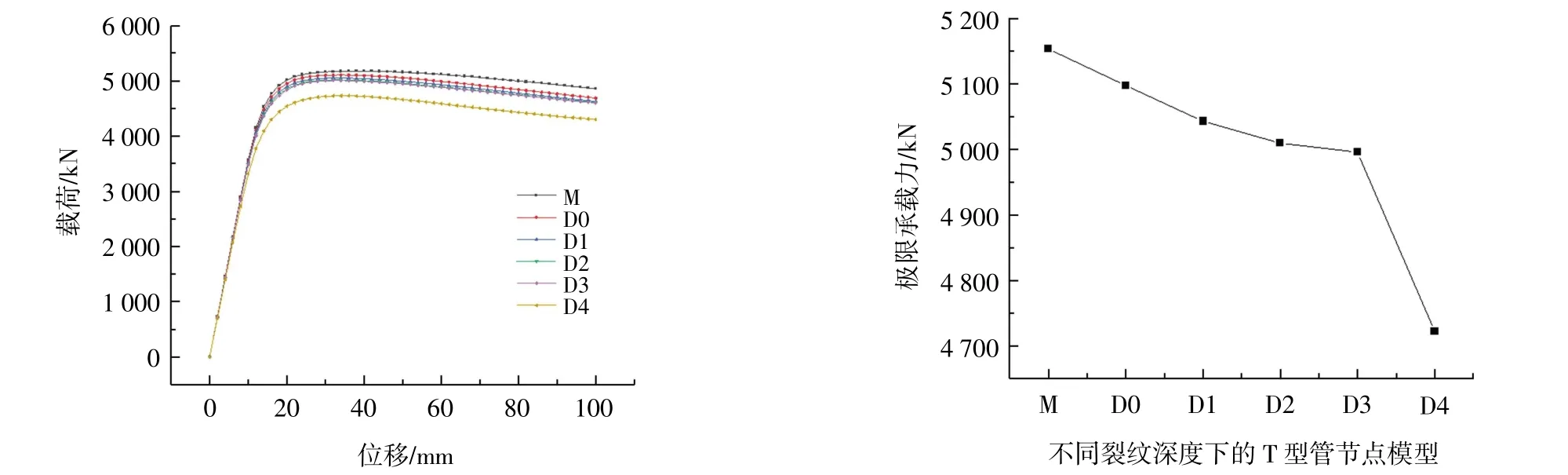
图9 不同裂纹深度的承载力曲线

将单裂纹模型的长度和深度损伤参数放在一起进行对照分析，通过图10 可以看出，裂纹扩展的前中期，随着裂纹深度的加深，极限承载力的弱化比较明显，裂纹的深度对极限承载力影响比较大；裂纹发展的后期，当出现贯穿裂纹时，管节点结构出现严重破坏，极限承载力会大幅度下降。

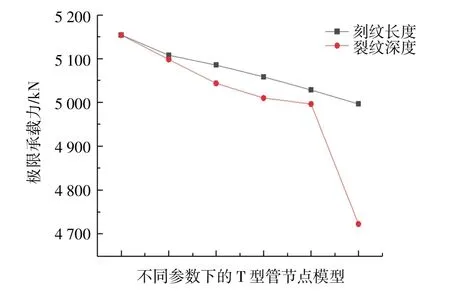
图10 不同裂纹参数的极限承载力曲线

2.2 腐蚀参数的影响

2.2.1 点蚀坑位置

根据表6 中单腐蚀模型S0～S4 的计算结果，管节点在只受腐蚀损伤下，单个腐蚀坑下管节点的极限承载力率很小。根据图11 可以看出，单个腐蚀坑的位置越远离焊缝相贯线，则对管节点极限承载力的影响越小，且总体上点蚀引起的单个腐蚀坑对管节点承载力的影响极小。因此，老平台管节点附近出现轻度点蚀情况下，平台结构安全性不受较大影响。

图11 腐蚀坑在不同位置下承载力曲线

2.2.2 材料腐蚀修正模型

图12 是通过是否采用修正三折线本构模型，来分析材料本构模型修正对管节点极限承载力的影响。根据表6 中单腐蚀模型P0～P1 的计算结果来看，在未使用本构修正模型前，其极限承载力折减率为-1.58%，使用修正本构模型后极限承载力折减率为-3.34%。从而可以看出，采用修正三折线本构模型时，能更准确地预测管节点实际承载力变化情况。

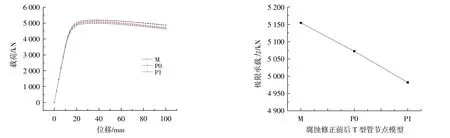
图12 采用修正三折线本构模型前后极限承载力曲线

图13 是通过采用修正三折线模型，来分析不同腐蚀率对管节点极限承载力的影响。从图上来看，腐蚀率的增加与极限承载力的减弱呈类线性变化；根据表6 中单腐蚀模型P1～P5 的计算结果来看，随着腐蚀率的增加，其极限承载力折减率逐渐减小，管节点的极限承载力也逐渐变小；当腐蚀率为6%时，折减率达到了-8.23%，与出现贯穿裂纹时的折减率相类似。工程实际中，贯穿裂纹的发生相比管节点的腐蚀需要的条件更为严苛，因此随着平台服役的后期，腐蚀率的上升，极限承载力的弱化对腐蚀更敏感。

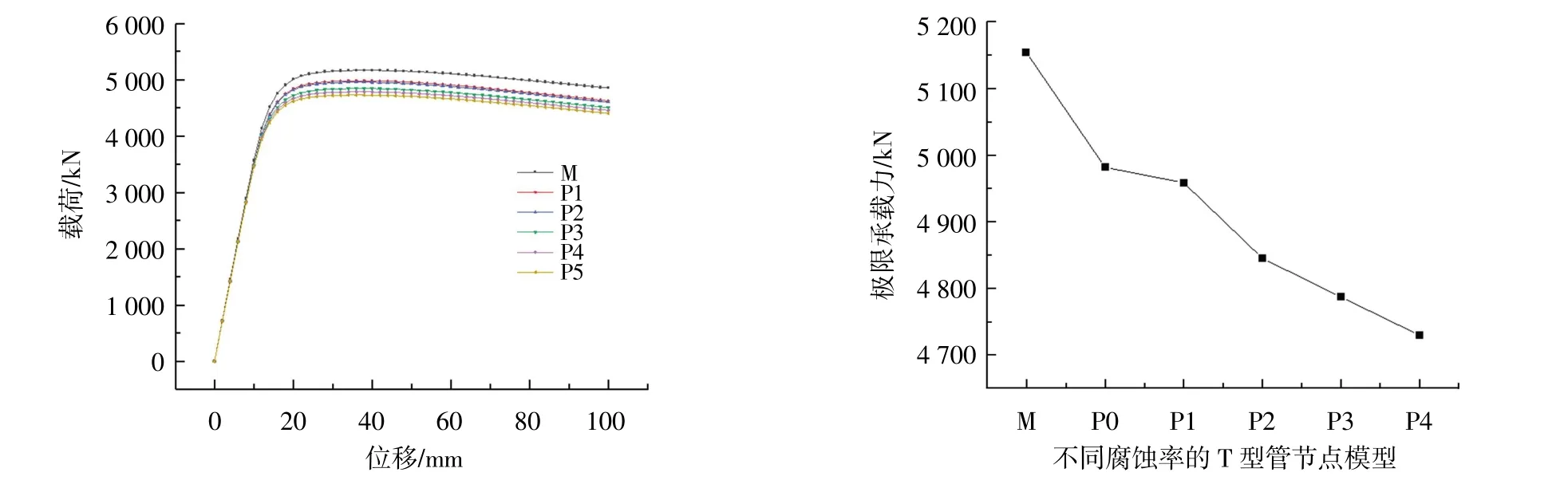
图13 不同腐蚀率下的极限承载力曲线

2.3 裂纹与腐蚀联合作用的影响

实际工程中，老龄平台上腐蚀与裂纹通常是同时存在。图14 是裂纹腐蚀联合作用下对管节点极限承载力的影响，从图中可以看出R1 模型的极限承载力最小。根据表6 中裂纹腐蚀联合模型R0～R3的计算结果表明，裂纹与腐蚀相对位置在0°和180°时具有相似的管节点极限承载力折减率，说明单裂纹与单腐蚀坑的耦合作用对极限承载力的影响较小，而其折减率大约为两种损伤的单独作用下的保守相加；而在裂纹布置在90°时极限承载力折减率下降较大，说明在轻度腐蚀损伤和裂纹损伤联合作用下，裂纹损伤的影响占主导地位。

图14 不同损伤状态下的极限承载力曲线

3 结 论

本文选择赵东ODA 平台的典型T 型管节点，围绕裂纹长度与深度、腐蚀坑相对位置分布、材料本构的模型修正及腐蚀与裂纹联合作用对管节点极限承载力的影响，基于非线性有限元分析研究了腐蚀与裂纹损伤对管节点极限承载力的影响规律，获得以下主要结论。

（1）管节点位置裂纹的出现，特别是贯穿裂纹的产生，将使得管节点的极限承载力大幅度下降；（2）管节点位置腐蚀坑的出现，随点蚀坑与主支管相贯位置的远近发生变化，但总体影响较小；（3）使用修正三折线模型能更准确地预测管节点腐蚀影响的极限承载力弱化规律；（4）综合考虑裂纹与腐蚀联合作用时，节点极限承载力的弱化中裂纹起主导作用。

本文的研究成果为我国老平台延寿评估提供了技术支持，为实际工程中老平台的延寿分析指明了方向。