基于主余震理论的余震地震动PGA衰减关系研究

施雨捷，芮 佳，3*，黄小宁，王皓冬

(1.青海大学土木工程学院，青海 西宁 810016； 2.青海省建筑节能材料与工程安全重点实验室，青海 西宁 810016；3.甘肃省建筑设计研究院，甘肃 兰州 730030)

强烈地震发生后往往会伴随多次余震，而很多建筑结构在主震作用下能够保持相对完好，但是在余震作用下会出现损伤甚至倒塌的情况。地震动特性(幅值、持时、频谱特性等)和建筑结构在地震作用下的响应有密切关系，因此有必要掌握地震动本身的参数信息，从而对建筑结构在地震作用下的响应有进一步的了解。目前，许多学者专注于建立和优化地震动的衰减关系，他们在研究中大多将地震动参数转化为震级、断层距、剪切波速和其他场地条件的函数。Boore等[1-2]、Campbell[3]和Graizer等[4]在研究地震动的衰减关系时并未考虑余震对衰减结果的影响；而Abrahamson[5-6]、Chiou等[7-8]虽然在构建地震动参数衰减方程时将余震纳入考虑范围，但是仅仅将其看作衰减方程的影响参数，并未考虑不同余震的差异性。

本文基于NGA-West 2中学者提出的模型[1-12]，考虑了余震地震参数，研究余震相对地震动参数和地震参数及场地参数之间的规律；从PEER数据库中选择752组主余震地震动序列，归纳建立衰减关系，通过多元非线性回归方法回归出了余震相对地震动参数的变化规律，为地震危险性分析和工程实践提供一定的理论依据。

1 地震动数据库

建立地震序列数据库是分析建筑结构地震响应的前提。本文根据下列要求[4-5，8-16]选择合适的地震序列：(1)同一序列的主震和余震均来自于同一台站；(2)所选地震序列各项参数均有效；(3)不考虑双主震情况，剔除余震峰值加速度大于主震峰值加速度的数据；(4)所有地震序列均为壳内地震序列；(5)去除峰值加速度小于0.03 g的地震序列；(6)所有地震序列需要相应的场地条件数据；(7)剔除震源距过小的地震序列；(8)地震序列均记录于自由场地。根据蒙特卡洛原理，从美国太平洋地震研究中心的下一代地震衰减数据库中选用752组真实记录的主余震地震动序列[11]，分别来自11条地震序列，有183个台站记录。根据主震序列和余震时间区分的地震动数据及其台站情况如表1所示。

表1 主余震序列相关信息Tab.1 Information of main and aftershock sequence

2 余震地震动PGA衰减模型

2.1 衰减模型的建立

根据相关学者[1-10,12]提出的NGA-West2地震动衰减关系，统计本文选取的地震序列数据库中的数据变化规律，提出下列余震地震动参数的衰减关系：

(1)

式中：Y表示地震动强度参数IM，本文为地震峰值加速度PGA；∇Y表示相对地震动强度参数，本文为余震峰值加速度与主震峰值加速度的比值∇PGA；Mms表示主震矩震级；∇M表示相对震级，本文为余震震级与主震震级的比值；Vref表示特定的参考速度，本文为美国地震减灾计划NEHRP中B类和C类场地的剪切波速界限值，取760 m/s；VS30表示地下30 m的平均剪切波速；Dms表示主震的断层距；ε表示计算值和实际数据之间的残差；b1-b4表示公式的回归系数。

在公式(1)中，等号右边第一项和第二项用于描述∇Y随地震参数的变化情况，第三项模拟场地参数对∇Y的影响，第四项表示传播参数对∇Y的几何影响。采用最小二乘法进行回归，主要基于3个假设：(1)期望函数的形式正确；(2)随机噪声服从均值为零的正态分布，各个随机项之间相互独立，且方差是常数；(3)期望函数和随机噪声之间相互独立。

2.2 回归结果

根据最小二乘法原理[13]，编写Matlab代码进行非线性回归，得到对应本文地震峰值加速度PGA的拟合系数和标准差，上述公式代入回归系数可写为：

(2)

式中：ε满足均值为0，标准差为0.497 6的正态分布。

图1为不同主震震级对应的∇PGA随场地剪切波速VS30变化的数学关系。从图1可以看出，相对地震动参数和主震矩震级之间呈正相关，符合系数b1取值的数学规律。

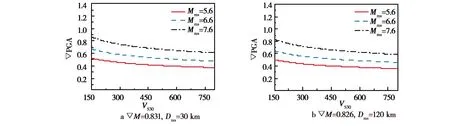
图1 不同Mms对应的∇PGA随VS30的变化Fig.1 Variation of ∇PGA with VS30 corresponding to different Mms

图2为不同余震震级对应的∇PGA随场地剪切波速VS30变化的数学关系。从图2可以看出，相对地震动参数和主余震震级之比呈负相关，符合系数b2取值的数学规律。

图2 不同∇M对应的∇PGA随VS30的变化Fig.2 Variation of ∇PGA with VS30 corresponding to different ∇M

图3为∇PGA随场地剪切波速Dms变化的数学关系。从图3可以看出，相对地震动参数和标准场地剪切波速之比呈正相关，与VS30呈负相关。

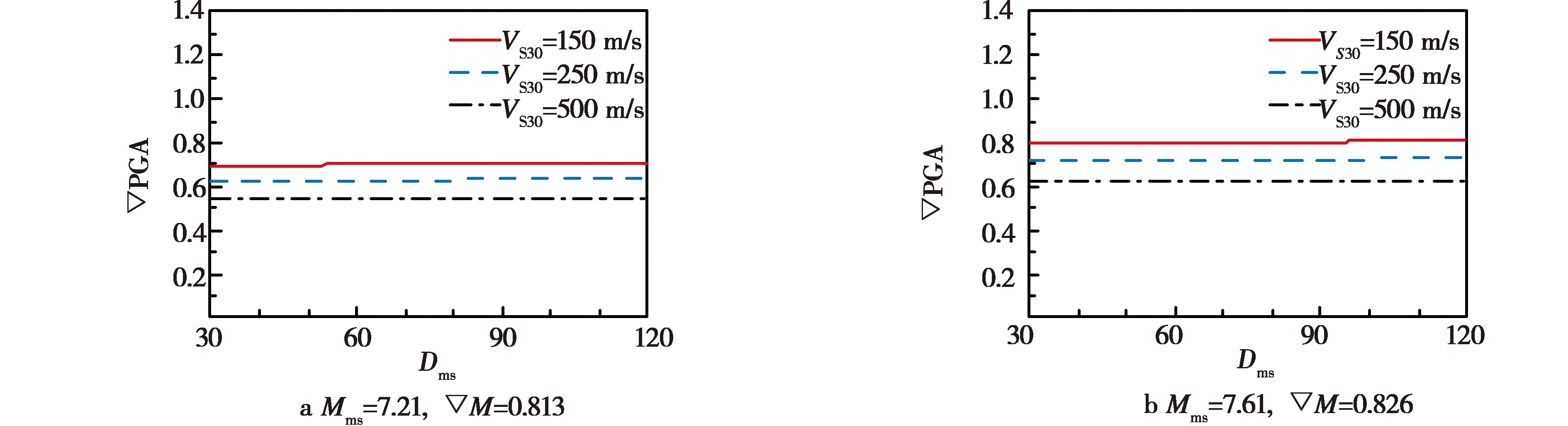
图3 不同VS30对应的∇PGA随Dms的变化Fig.3 Variation of ∇PGA with Dmscorresponding to different VS30

图4为不同主震震源距对应的∇PGA随场地剪切波速VS30变化的数学关系。结合b4的值及图4的结果可以看出，主震的震源距对∇Y的影响很小，以VS30=300 m/s为例，当震源距从30 km提高到120 km时，∇Y的增加幅度仅为2%，变化较小。

图4 不同Dms对应的∇PGA随VS30的变化Fig.4 Variation of ∇PGA with VS30 corresponding to different Dms

2.3 回归结果合理性判定

为了验证本次非线性回归的科学性和合理性，对本次回归的数据和结果进行对比分析。本文参考相关[14-15]研究，根据如下公式将所有的地震数据规范化：

ln(obsnor)=ln(obs)-ln(pre)+ln(prenor)

(3)

式中：obsnor是规范化后的统计值，obs是统计值，pre是根据实际地震动数据的公式计算估计值，prenor是在标准条件下的公式计算估计值。

图5、图6和图7为两种标准条件下计算估计值和规范化统计值的统计图，可以看出，在这两种标准条件下，大部分计算估计值都在16%和84%虚线以内。根据标准正态分布理论可知，本文构建的模型能较好地回归出余震相对地震动参数的统计规律，从而说明本文假定的正确性。

图5 计算估计值和规范化统计值随场地剪切波速变化关系的比较Fig.5 Comparison of prenor and obsnor with the variation of shear wave velocity

图6 计算估计值和规范化统计值随震源距变化关系的比较Fig.6 Comparison of prenor and obsnor with the variation of hypocentral distance

图7 计算估计值和规范化统计值随主余震震级比变化关系的比较Fig.7 Comparison of prenor and obsnor with the variation of magnitude ratio of main aftershocks

3 分析与对比

3.1 残差分析

本文参考相关学者[12,16-17]采用的对数残差理论验证所构建的模型是否符合统计学规律，对数残差为统计值的对数减去计算估计值的对数，如下列公式所示：

Re=ln(obs)-ln(pre)

(4)

式中：Re为对数残差，obs为统计值，pre为计算估计值。

图8分别为对数残差与主震震级Mms、震级之比∇M、场地剪切波速VS30和主震震源距Dms的关系。从图8可以看出，当主震震级Mms、震级之比∇M和场地剪切波速VS30、主震震源距Dms变化时，事件间的残差都均匀分布在零值附近，没有出现相应的趋势和偏差，说明本次预测结果和主震震级、主余震震级之比、场地剪切波速以及主震震源距之间相对无偏差。

图8 对数残差与主震震级Mms、相对震级∇M、场地剪切波速VS30、主震震源距Dms的关系图Fig.8 Relationship between Log Residuals and Mms，∇M，VS30 and Dms

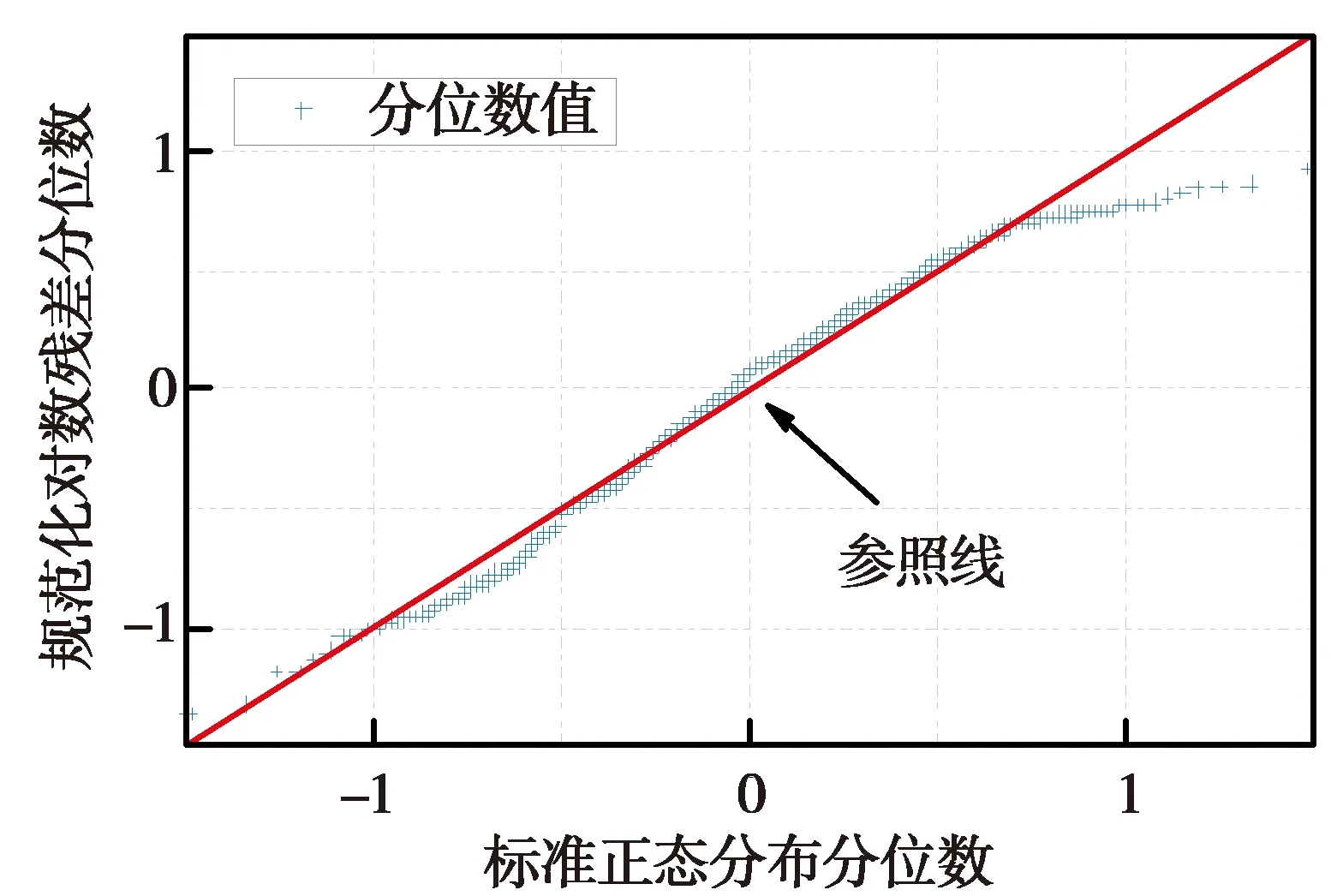
图9 对数残差的正态Q-Q散点图Fig.9 Normal Q-Q scatter plot of Log Residuals

根据Abrahamson[18]和Jayaram等[19]的理论可知，对数残差分布通常和正态分布存在某种联系。图9为对数残差和标准正态分布的Q-Q散点图，横坐标为标准正态分布分位数，纵坐标为规范化对数残差分位数。所有的离散分位数据都可以近似看成一条斜率为1的直线。根据Q-Q散点图的定义，当离散分位数据近似为一条斜率为1的直线时，可以认为两个数据的分布规律一致,说明本次规范化对数残差和标准正态分布属于同一分布，与前人的研究[18-19]结果一致，且符合最小二乘法的计算假定。

3.2 与其他模型的比较

在现有的地震动参数衰减关系中，选取精确度较高的AS2008和CY2008两大统计模型与本文所构建的模型进行比较，分析其联系和差异。根据Chi-Chi地震参数，本文采用Mms=7.2，Mas=5.9，Dms=90 km，VS30=360 m/s；Mms=7.6，Mas=6.2，Dms=30 km，VS30=250 m/s作为标准条件。图10为两种标准条件下不同模型计算的∇PGA随VS30变化的数学关系。根据图10可知，VS30在150～220 m/s时，本文构建的模型和CY2008模型的回归相似度较高，说明本文模型在VS30取值较小时可以展现合适的回归结果；当VS30从220 m/s增加至750 m/s时，本文模型和AS2008模型的回归相似度十分接近，最大误差仅为5%，说明本文模型在VS30取值较大时能更好地体现拟合性。此外，通过比较分析可知，本文所构建的模型能在场地剪切波速变化的情况下保证估算值的偏大性，在工程应用中较为安全。

图10 不同预测模型的比较图Fig.10 Comparison of different prediction models

4 讨论与结论

了解主震和余震地震动参数及地震参数之间的关系，可以在地震危险性分析中使用主震的地震参数数据计算出余震相对地震动强度，为地震危险性分析提供依据。前人主要对主震的地震参数进行分析[1-10,12,16-17]，大部分学者仅仅将余震作为一个固定的常数纳入衰减关系，并没有考虑余震具体的地震参数。因此，将余震地震参数纳入衰减方程，分析和研究余震相对地震动强度，有利于提高预测方程的精度，对地震危险性分析具有重要意义。本文基于NGA-West2中学者提出的模型，将余震地震参数纳入考虑，研究了余震相对地震动参数和地震参数及场地参数之间的统计规律。从PEER数据库中选择752组主余震地震动序列，归纳建立衰减关系，通过多元非线性回归方法回归出了余震相对地震动参数的变化规律，并得出以下结论：

(1)相对地震动参数和主震矩震级及标准场地剪切波速之比呈正相关，和主余震震级及场地剪切波速之比呈负相关，和主震震源距Dms之间的关系较小。

(2)本文模型的残差与震级之比∇M、场地剪切波速VS30、主震震源距Dms无关。根据Q-Q Plot的表现来看，相对地震动参数服从对数正态分布。

(3)通过与AS2008及CY2008模型进行比较可知，本文模型的预测值在VS30较小时和CY2008模型的预测值较为接近，在VS30取值较大时和AS2008模型的最大误差仅为5%，说明本文的回归模型表现较好。