弱可压δ-SPH算法在溃坝流中的应用
2022-06-20高仁祖顾声龙牛恒岗
高仁祖,顾声龙 ,牛恒岗
(1.青海大学水利电力学院,青海 西宁 810016; 2.黄河上游生态保护与高质量发展实验室,青海 西宁 810016)
光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)是一种基于光滑过程的无网格拉格朗日格式。该方法将计算区域(材料)离散为一系列的粒子,这些粒子具有质量、体积、速度、加速度和温度等物理量,粒子的集合表达了材料区域的物理量,而粒子之间通过核函数相互作用。SPH方法首次被Gingold等[1]提出,并在流体动力学中运用。近20年来,由于SPH方法在解决复杂的自由表面流上有独特的优势,在溃坝流动[2]、圆柱绕流[3]、近海岸波浪破碎[4]、多相流[5]、流体—结构相互作用[6]、河流冰动力[7]、浅水应用方面[8-9]等方面得到广泛应用。
近年来,许多研究人员对SPH方法进行完善和改进,特别是在计算精度及计算效率方面不断探索,试图得到更为准确的模拟结果,以便在更多的工程中进行应用。SPH方法通常分为弱可压SPH方法和不可压SPH方法。对于前者,会使用状态方程把压力场和密度场联系起来[10];对于后者,压力是通过求解Poisson方程来确定的[11]。通常,弱可压格式更适合自由表面流,因为沿自由表面的边界条件是隐式满足的,这意味着在流动变化过程中,弱可压格式不需要对自由表面进行显式检测。但是,弱可压格式的一个主要缺点是在压力和密度场中会产生虚假的数值振荡。为了消除或者减少虚假的数值振荡,Monaghan等[12]在一维激波问题中引入了一个基于Neumann-Richtmeyer人工黏性的人工黏性项,为了抑制冲击波中出现的振荡,这种人工黏性项有助于稳定SPH算法和减少其虚假的振荡。Andrea等[13]提出了一种人工黏性项修正的形式,用最小二乘法积分插值来滤除密度场,并在程序中给出了结果。Ferrari等[14]在Rusanov通量的基础上建立了一个数值扩散项,这一项已被添加到连续性方程中,以减少密度场内部的数值噪声。Molteni等[15]也提出了相应的数值扩散项,并在连续性方程中运用。这些扩散项的加入给出了很好的计算结果,但是与流体静力解不符。Molteni等[15]通过引入一个阈值密度来避免这个问题,这样扩散项只在压力超过流体静力解时起作用,可是这种策略导致了扩散项作用的急剧减少。
基于以上问题,Antuono等[16]对Molteni等[15]提出的扩散项进行修正,重新定义了一个新的方程组,其扩散项都包含在连续性方程和能量方程中,其黏性项包含在动量方程中,其中扩散项系数δ和黏性项系数α均是人为可调的参数,目的是解决密度不连续所带来的数值计算不稳定问题,以及减小虚假的高频噪声;其动量方程与具有人工黏性项的标准弱可压SPH格式一致,被证明与流体静力解相符,并适当地消除了压力场和密度场的虚假数值振荡。
本文基于Antuono等[16]提出的具有扩散项的SPH格式,自主开发δ-SPH算法程序,探讨与研究具有该扩散项的SPH方法在自由表面流方面的应用。
1 模拟方法
1.1 质量守恒方程
在拉格朗日型式下的弱可压牛顿流体的连续性方程表示为:
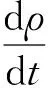
(1)
方程(1)中,u为速度矢量,ρ为流体密度,p是关于密度变化的压力场。
弱可压SPH模型中,状态方程[17]为:
(2)
方程(2)中,c0和ρ0分别是流体的声速与初始流体密度。为满足弱可压条件,要求密度的波动范围小于1%ρ0[17]。在流体计算域Ω内,需要设置全局初始声速c0,并且满足[18]:
(3)
通过推导将连续性方程转化为离散化的SPH形式[17]:
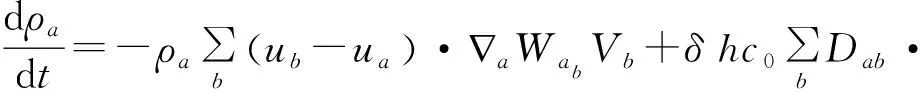
(4)
连续性方程(4)中,扩散项Dab可以表示为:
(5)
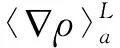
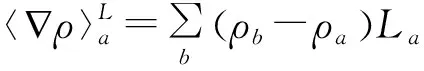
(6)
(7)
方程(7)中,下标a、b代表计算域内任意2个粒子,∇a表示相对于粒子a坐标的梯度算子,Wab表示光滑核函数(本文使用Wendland C2核函数[19]),ρa和ua分别是第a个粒子的密度、速度矢量,Va是a粒子影响域的面积(本文计算域Ω是二维的),δ是人为可调的扩散项系数。
1.2 动量守恒方程
根据动量守恒定律,流体的动量方程如下:
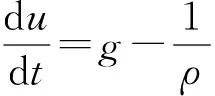
(8)
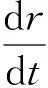
(9)
在方程(8)和方程(9)中,g和r分别代表流体的重力加速度和位置矢量,p是关于密度变化的压力场,V是黏性应力张量,对于牛顿流体,可以表示为:
V=λtr(D)I+2μD
(10)

其离散化的SPH形式[17]为:
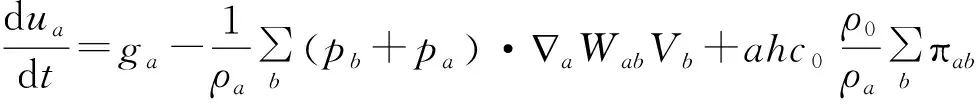
(11)
(12)
(13)
上式中,pa、ga和ra分别是第a个粒子的压力、重力加速度和位置矢量,α是人为可调的黏性项系数。
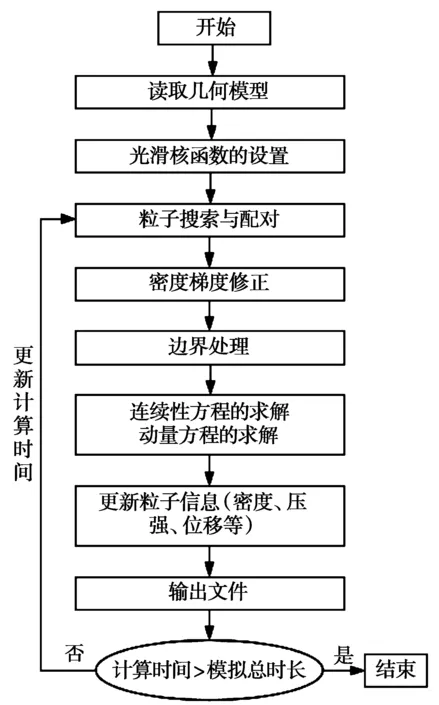
图1 程序流程图Fig.1 Program flow chart
2 模拟工况设计
2.1 计算流程
开发的C++δ-SPH模型程序的基本程序流程图如图1所示。流程第一步:读取几何模型,并对几何模型(计算域)进行粒子化处理;流程第二步:选取或者设置光滑核函数(核函数的选取只是在程序里选择哪一种核函数来参与计算,并没有提前遍历求解出每个粒子的核函数及偏导数,而是每次遍历粒子需要时,才去求解该粒子所需的核函数及偏导数);流程第三步:对每个粒子进行粒子配对,其邻近粒子搜索用到了链表搜索法;流程第四步:遍历每个粒子,通过上述公式(6)进行密度梯度修正,以确保在自由表面处核函数粒子缺失条件下,密度梯度具有二阶精度,此步的计算结果参与第六步的计算;流程第五步:通过虚粒子法进行固壁边界处理,其中遍历每个虚粒子,通过状态方程反推出它们的密度;流程第六步:遍历每个流体粒子,求解上述方程(4)和方程(11)的左项;流程第七步:时间进程采用蛙跳法推进每一步求解,并且每500步输出1次文件;流程最终需要进行计算时间的判断,直到计算达到要求。
2.2 边界条件的处理
SPH方法中,靠近边界的流体粒子支持域内只有部分粒子,在固壁边界外无流体粒子,出现了积分被边界截断的问题,造成边界附近的粒子穿过边界,因此需对固壁边界进行处理,以获得正确的计算结果。本文使用Adami等[20]提出的一种在流体外布置多层虚粒子实施固壁边界的方法,这种方法直接将内部流体粒子的压力插值到虚粒子上,如方程(14),再利用状态方程反推出虚粒子的密度,虚粒子通过压力梯度对流体施加边界力,该边界处理方法对复杂几何边界问题应用很好。
(14)
上式中,ab表示虚粒子的加速度。
2.3 经典溃坝案例
本研究采用经典溃坝案例进行测试,并与Lobovsky等[21]研究得出的实验值做对比分析,数值模拟与实验的比尺Lb=3。Lobovsky等[21]的实验模型以水箱里面的水体布置设置了2组工况,分别为水深600 mm和300 mm,其中水箱长度设置为1 610 mm,高为600 mm,水体长为600 mm。本文选取工况为水深300 mm 进行对比分析,数值模型初始布置如图2所示。初始的水箱长度设置为L=537 mm,在水箱里布置长L1为200 mm和d为100 mm的矩形流体区域。粒子初始间距为1 mm,流体粒子总数为2万个,时间步长为10-4s,模拟总时长为10 s。图2中横、纵坐标以量纲化X/d、Z/d的形式给出。图2中右下角P1和P2点为压力监测点,其坐标分别为5.42,0.05和5.42,0.32;在Lobovsky等[21]实验中对应的监测点为Sensor 1和Sensor 4。

图2 溃坝数值模拟模型示意图Fig.2 Schematic diagram of numerical simulation model of dam break
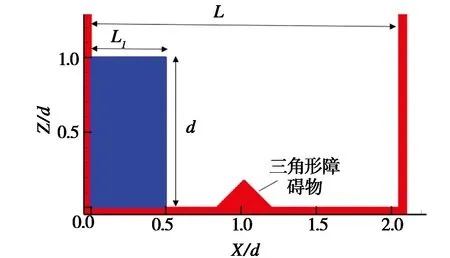
图3 数值模拟模型示意图Fig.3 Schematic diagram of numerical simulation model
2.4 带有三角形障碍物的经典溃坝案例
由于没有实际溃坝工况,本研究设计了带有三角形障碍物的经典溃坝案例,在标准SPH中加入扩散项之后进行测试。数值模型的初始布置如图3所示。初始的水箱长度设置为L=2.05,在水箱里布置长L1为0.5和d为1.0的矩形流体区域。粒子初始间距为0.01,流体粒子总数为5 000个,时间步长为10-4s,模拟总时长为10 s。
3 结果及分析
3.1 经典溃坝案例模拟结果的分析
在此次测试案例中,选取了黏性项系数α为0.02,并考虑标准SPH格式(即没有扩散项的SPH模型)与具有扩散项的SPH格式(扩散项系数δ取0.1)。为了研究压力场和密度场的虚假数值振荡问题,在状态方程中,压强是密度的函数,因此,本研究数值模拟的参数以压强为主,最终通过压强的波动变化来分析其虚假数值振荡问题。图4给出了两种SPH格式下不同时间的压强变化云图,时间以无量纲的形式表示为t(g/d)1/2,监测点处的压强以无量纲的形式表示为P/ρgd。从图4a组与图4b组的对比发现,在图4a组左图的近壁面流体压强色值及右图的压强变化色值明显比较紊乱,其主要原因是在标准SPH格式下,数值在模拟的过程中产生了虚假的数值振荡,为此在连续性方程中考虑Antuono等[16]的扩散项,得到图4b组压强变化云图。在两种不同时间下给出的压强变化云图结果明显改善,压强色值变化明显,比图4a组呈现规律分布。
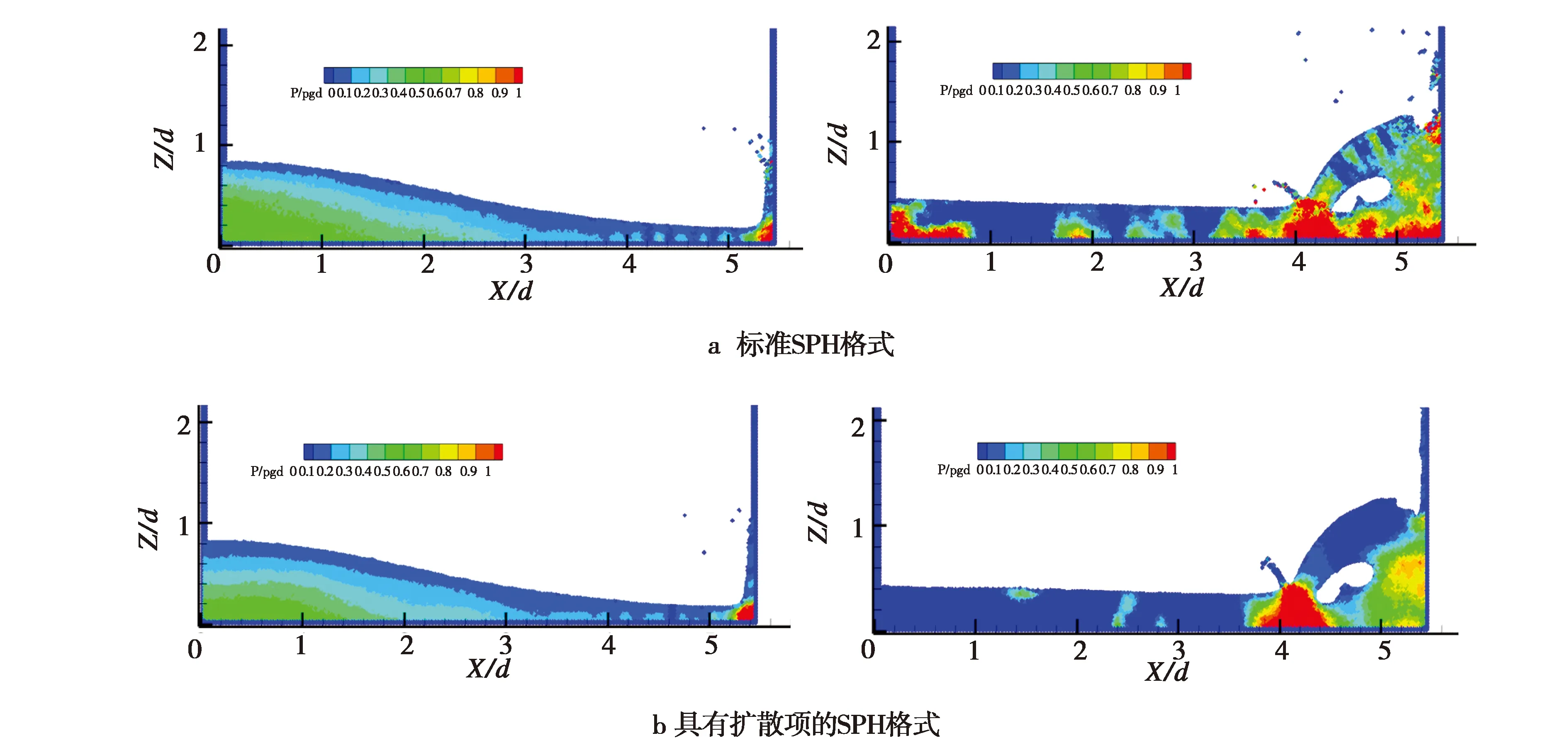
图4 t(g/d)1/2=2.81与t(g/d)1/2=6.59时的压强变化云图Fig.4 Nephogram of pressure variation when t(g/d)1/2=2.81 and t(g/d)1/2=6.59
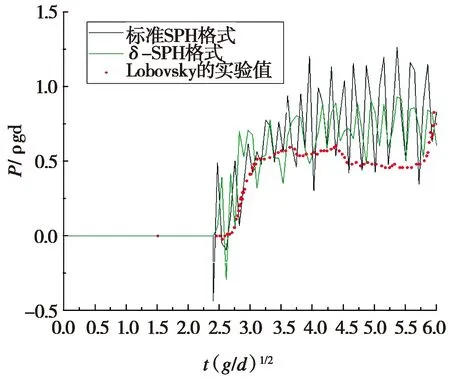
图5 监测点P2处随时间变化的压强曲线分布图Fig.5 Pressure curve of monitoring point P2 with time
图5给出了监测点P2处随时间变化的压强曲线分布图。红点曲线表示Lobovsky等[21]的实验值;黑实线代表原有的标准SPH格式数值模拟得到的压强检测结果,时间t(g/d)1/2范围为3.0~6.0时,数值上下振荡较为严重,监测点处的压强振荡范围为0.3~1.3;绿实线代表经过扩散项处理后的SPH数值计算的结果。在原有弱可压SPH格式的连续性方程中加入扩散项后,监测点处的压强振荡范围为0.4~0.8,明显削弱了虚假的数值振荡,波动范围的削减意味着降低了弱可压SPH中的密度和压力场虚假数值振荡的影响。
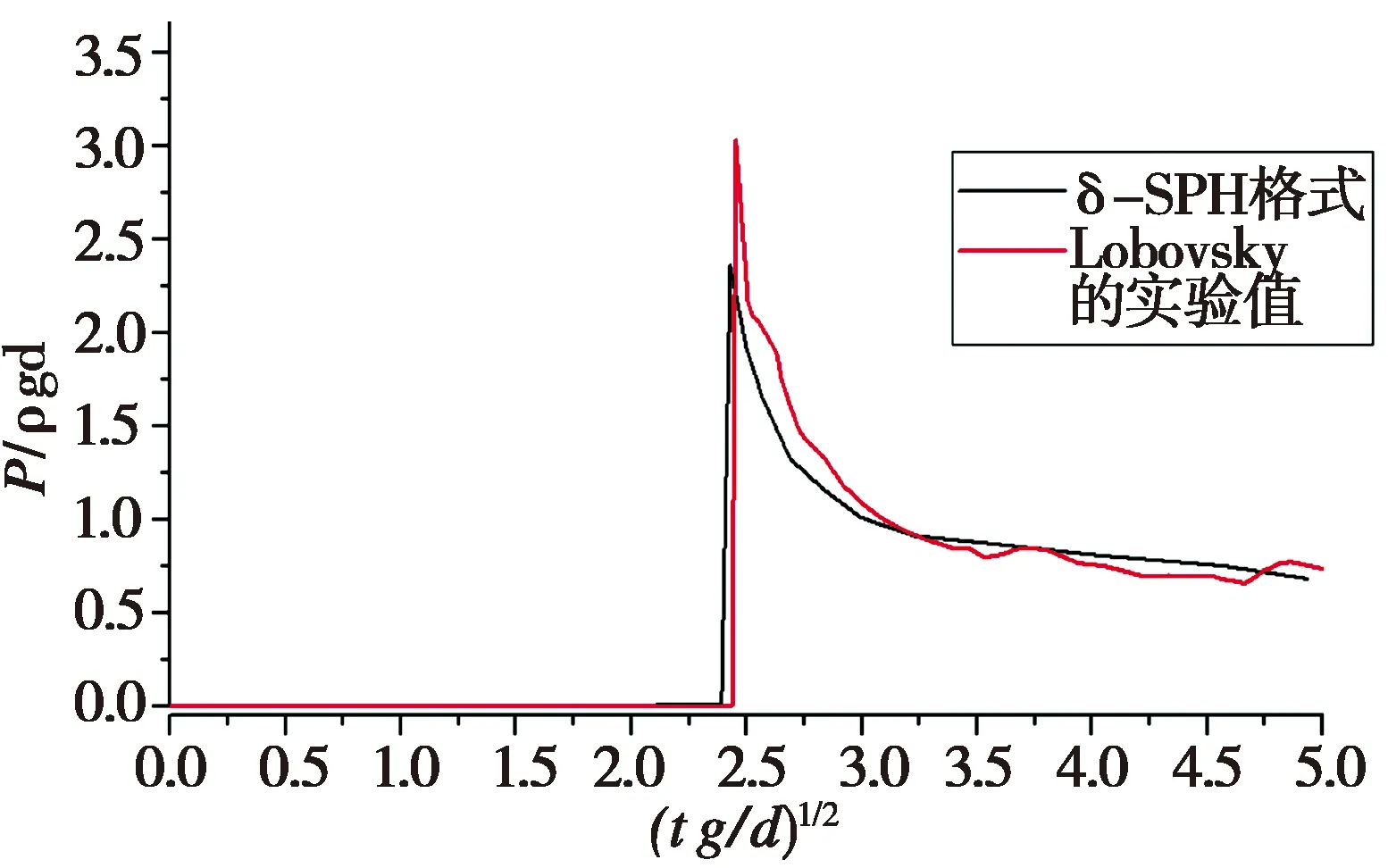
图6 监测点P1处随时间变化的压强曲线分布图Fig.6 Pressure curve of monitoring point P1 with time
图6为监测点P1处随时间变化的压强曲线分布图。对基于δ-SPH方法得到的数据进行了曲线拟合处理,从图6发现,具有扩散项的SPH格式所得到的数值模拟结果与Lobovsky等[21]的实验值吻合较好,在t(g/d)1/2=2.4时,压强曲线呈突增趋势,随后又缓慢下降,此时,流体流动处于溃坝后碰撞另一侧壁面及沿壁面向上流动的状态。数值模拟结果与实验结果的平均误差为7%。本实验采用误差分析标准,其误差分析是根据监测点处各段时刻取实验值及模拟值作为误差,最后对这些误差进行求和、求平均得到最终的平均误差。
综上所述,在连续性方程中考虑Antuono等[16]的扩散项之后,有效地改善了数值模拟结果。在压力监测点的曲线图中,实验值变化趋势和数值变化趋势一致,说明本次开发的算法程序可以很好地应用于自由表面流方面。
3.2 带有三角形障碍物的经典溃坝案例模拟结果的分析
图7给出了t=0.26 s与t=0.46 s时的压强变化云图。图7a组图通过标准的SPH格式数值模拟得到。从图7a中发现,左图压强色值变化分层不明显,局部色值及右图延伸出来的水舌部分色值明显紊乱,局部的压强大于0值,这些现象都是由虚假的数值振荡造成的。图7b组图是具有扩散项的SPH格式数值模拟得到。从图7b可以清晰看出,压强色值分层明显,且水舌的色值基本趋于0值,相比于图7a组图,在SPH中加入扩散项后,压强云图效果明显改善。
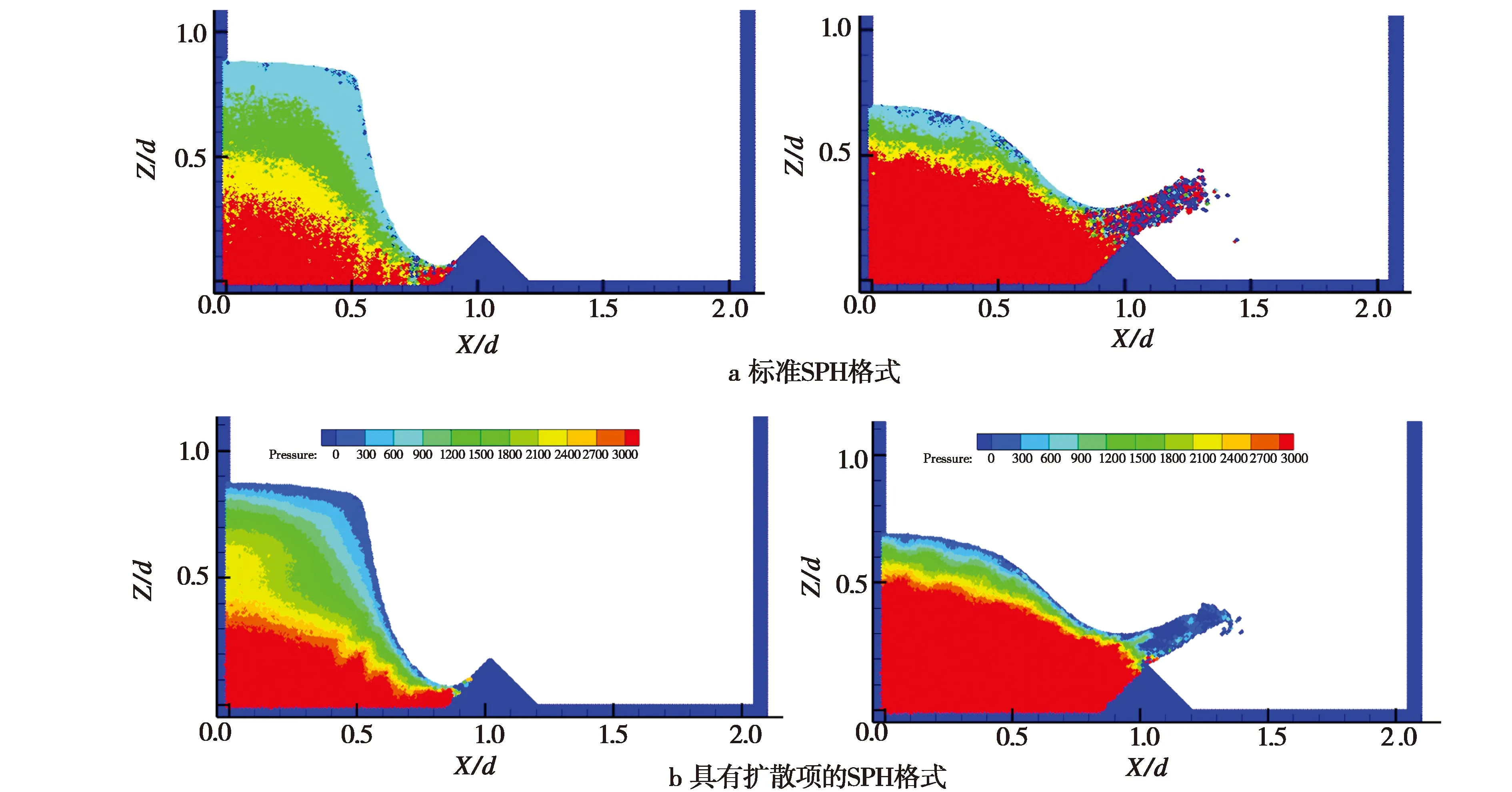
图7 t=0.26 s与t=0.46 s时的压强变化云图Fig.7 Nephogram of pressure variation when t=0.26 s and t=0.46 s
4 讨论与结论
近些年,相关研究不断地改进SPH方法,尤其对于弱可压SPH方法。但在应用于自由表面流方面,连续性方程带来了数值振荡问题。为此,Monaghan等[12]、Andrea等[13]、Ferrari等[14]、Molteni等[15]、Antuono等[16]对此类数值振荡问题进行了研究,其中Antuono等[16]在弱可压SPH方法中解决数值振荡问题所给出的新格式δ-SPH最为先进,在连续性方程及能量守恒方程中加入扩散项,在动量守恒方程中加入了黏性项,其中扩散项系数δ和黏性项系数α对于不同流体流动情况可以进行人为调节,能够促使格式稳定,有效地解决了数值振荡问题,与流体静力解相符。
本文通过开发δ-SPH算法程序,对经典溃坝案例与带有三角形障碍物的溃坝案例进行数值模拟,得出以下结论:
(1)通过对δ-SPH算法的数值模拟结果与文献[21]实验结果的分析比较表明,标准的SPH格式数值模拟时受到虚假数值振荡的影响,加入人为可调系数的扩散项之后,数值模拟的结果明显改善。尤其在数值模拟三角形障碍物的溃坝案例中,扩散项的加入对模拟效果的改善更为直观。
(2)从图5和图6中发现,通过监测点P1处的压强检测数据,对数值模拟结果与实验结果进行对比分析,其变化趋势一致,平均误差在7%左右,验证了该算法具有很好的稳定性,体现了弱可压δ-SPH算法能很好地在溃坝流中进行应用。
(3)图5的标准SPH格式和δ-SPH格式数值模拟的压强随时间的波动变化说明了本次开发的δ-SPH算法,在一定程度上降低了虚假的数值高频波动,其改善效果明显。
