基于多层交通网络度-度距离模型的新冠肺炎传播研究
2022-06-20魏代俊
田 锋,魏代俊
(湖北民族大学数学与统计学院,湖北 恩施 445000)
随着新型冠状病毒肺炎疫情的爆发与蔓延,截止北京时间2020年8月20日,湖北累计报告了新冠确诊病例68 139例[1-3]. 2020年1月23日,为及时遏制新冠病毒随人口的流动迅速传播,武汉市政府于上午10时宣布全面关闭离汉通道. 基于百度迁徙和腾讯定位等地理位置服务所收集到的离汉人口迁出数,发现在1月10日至23日14 d期间约有500万人离开武汉,其中68.37%的迁出人口目的地在湖北境内,该阶段性数据在一定程度上可以说明从武汉迁出的这500万人口中,目的地在湖北境内的人口占比很大. 因此分析这部分人的流动对疫情研究有很大作用.
目前,基于人口迁徙数据对新冠病毒传染特性的建模研究分析已经取得了较好的成果:许小可在《新冠肺炎爆发前期武汉外流人口的地理去向分布及影响》一文中分析得出“封城”之前离开武汉的500万人口中大部分都不是社交媒体上热议的“逃离”,绝大部分还是像往常一样正常返乡过年,另外也得出2020年武汉春节外流人口的地理分布与正常年份相比两者之间没有明显差别[4-10];文献[11]提出了一个针对中国城市级传染病传播的通用模拟器模型,其可依据具体用途进行调整、也可有助于应急响应中的政策分析以及对未来公共卫生事件的早期预警[11];第一财经报道则从1月23日武汉宣布关闭离汉通道后的人口迁徙指数对比中说明即使在解封后离汉人口也并未出现“井喷”现象[12]. 同时还有数据统计4月8日解封当天离开武汉的人口中约78%的人口迁出目的地仍是湖北省内的其它城市,这一现象与解封之前武汉人口迁出情况相吻合[13-15].
目前已有的文章或通过统计分析或利用SIR模型对新冠疫情传播进行研究,相比之下从网络自身结构理论出发所做的分析还较少[16-21]. 2020年文献[22]提出了单层网络度-度距离的概念,其定义为两节点度值越接近,则距离越小,很直观地度量了网络中两个节点的相似程度,而城市间距离的度量也可超越传统意义上按照人口规模和空间地理位置的划分,借鉴度-度距离.
为此,本文把单层网络的度-度距离推广至多层,建立了湖北省内17个地级市之间的航空、铁路、高速公路3层交通网络. 在多层网络的基础上利用网络自身的结构特性对本次湖北省内的新冠疫情进行研究,本文研究的意义在于:一是区分不同交通方式在疫情传播中的不同作用;二是寻找到一种更加贴近实际的城市聚类方法,使得这种城市群的划分更能反映疫情的实际传播情况.
1 模型建立
1.1 相关知识
1.1.1 多层网络
图1 常见多层网络图Fig.1 Graph of common multi-layer network
单层网络一般用一元数组G=(V,E)来表示,V表示节点、E表示邻边.但在实际的生活中不仅存在单层网络,还存在很多复杂的多层网络,为了表示由多个单层网络组成的网络或者一个网络具有多种类型的边以及其余某些特征时,需要在单层的基础上通过引入不同的层或维度,即产生多层的概念.如:现实生活中两个人之间的关系可以是同事、也可以是朋友,这里的同事和朋友就可以划分为两个维度.一般的多层网络可以用多元数组G=(V,E,K)来表示,这里的V,E仍分别为节点和连边,K表示不同的维度,多层网络一般如图1所示.
1.1.2 度-度距离
给定一个网络G(V,E),其中每个节点i∈V都被自然地赋予了一个尺度pi(和i相连的节点数目),即网络的度,该尺度是独立于网络外在属性之外的,仅仅只由网络内部的拓扑结构所决定.每一个连边(i,j)∈E是一个二元数组,一般地,连边仅表示了两节点之间是否连接,其除非被赋予一些额外的属性(如权重或容量等),否则会因缺乏相应的可比较尺度从而导致无法对其在大多数复杂网络中展开统计研究[22].
基于此研究现状,周斌等[22]通过引入单层网络度-度距离来重新给边赋权体现出边的统计重要性,在给定的网络G中,度-度距离常用η(i,j)表示:
logη(i,j)=logη(j,i)=log|pi-pj|,(i,j)∈E.
(1)
从度量方式上看,logη比η或许更适合来定义距离,但是在后续的研究中发现就像网络的度p在传统的复杂网络幂律研究中所起的作用那样,η与logη在定义距离上起着相同的作用,因此仍然用η来定义距离,与此同时η和其概率分布P(η)都是服从幂律分布的.事实上,在假设大多数网络都是连通的前提下,η比p在任何情况下都具有更大的统计意义.
从定义可知度-度距离实质上度量了网络中两个节点的相似程度,直观上就是若两个节点的度-度距离越小(接近于1),则说明这两个节点越相似[23-30].同时η(i,j)是一个自然的尺度,其完全由网络拓扑结构来决定,也是一种无量纲的表示形式,因此定义式(1)可以改写为(2)式(即排序后两端节点的度之比):
(2)
从该式可以看出η的取值范围是[1,max{ki,i∈V}].
1.2 多层网络度-度距离模型
在1.1.2中介绍了单层网络度-度距离的定义,其从本质上反映了网络的内在特征.对多层网络而言其节点在不同层的代表意义不同,因此给多层网络度-度距离的计算带来了难度.
基于1.1.1中多层网络的理论部分介绍,其通常用多元数组G=(V,E,K)表示,其中的K即表示网络中不同的维度,笔者通过在多层网络中引入“某种因子ωi”把多层“折算”为单层的方法建立多层网络的度-度距离模型从而对其进行计算,建模步骤为:
第一步:考虑多层网络中各层的权重比例ωi使得:
(3)
第二步:根据权重比例计算各层中节点“折算”后的度,如设第i层中第j个节点度为pj,那么其折算后的节点度为:
(4)
第三步:由此得到多层网络中度-度距离模型为:
(5)
其中j,h表示多层网络中的节点.
2 基于多层网络度-度距离模型的疫情传播分析
2.1 数据来源
本文所用的2020年1月10日至23日期间每天从武汉迁入至湖北省内其它地级市(州)的人口比例数据来源于百度迁徙和腾讯位置服务平台,选取1月10日至23日的数据原因是:
(1)1月10日至23日处于2020年春运期,该时间段内人口的流动规模比平常更大,选其进行分析对结果更有说服力;
(2)武汉市于1月23日上午10时全面关闭离汉通道,选取关闭之后的时间对结果无意义;
(3)新冠的潜伏期大致为14 d,从10日到23日恰好约为一个潜伏期时间,这对统计累计确诊人数的结果更有价值.
由此得到了14 d内武汉依次迁出至孝感、黄冈、荆州等16个地区的人口比例(见表1);所收集的截止到8月20日湖北省内各地级市(州)累计确诊病例人数来源于腾讯健康中心;所统计的湖北省内3大交通的连接情况来源于航班管家、铁路12306、汽车客运中心出行APP.
表2为收集到的湖北省内各地区航空连通情况(铁路和公路的连通不再赘述),其中数字“1”表示两个地区之间可达、“0”表示不可达.

表1 武汉迁入各地区人数比例Table 1 Proportions of people moving into different regions in Wuhan
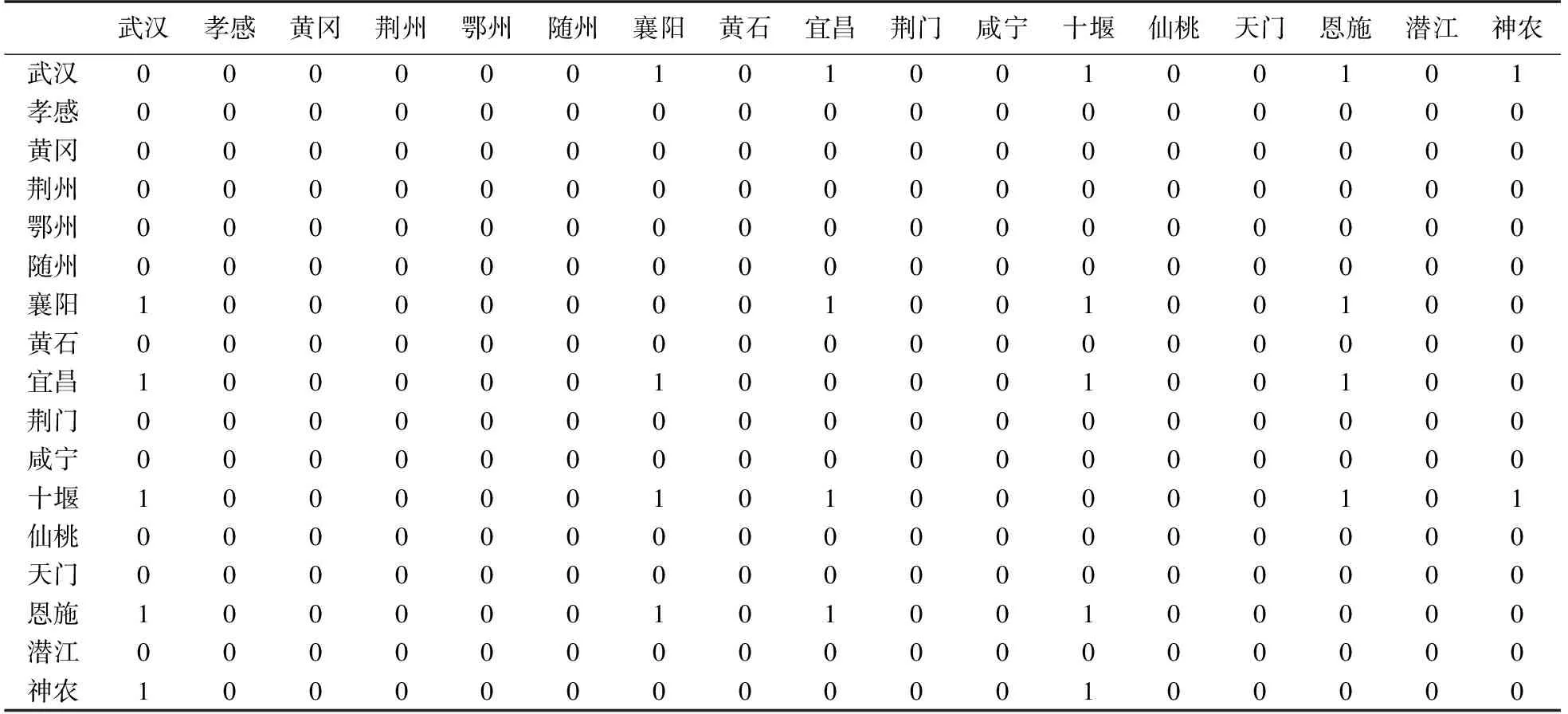
表2 湖北各地区飞机连通情况Table 2 Airplane connectivity in various regions of Hubei
2.2 统计分析
2.2.1 迁入人口比例与确诊人数关系研究
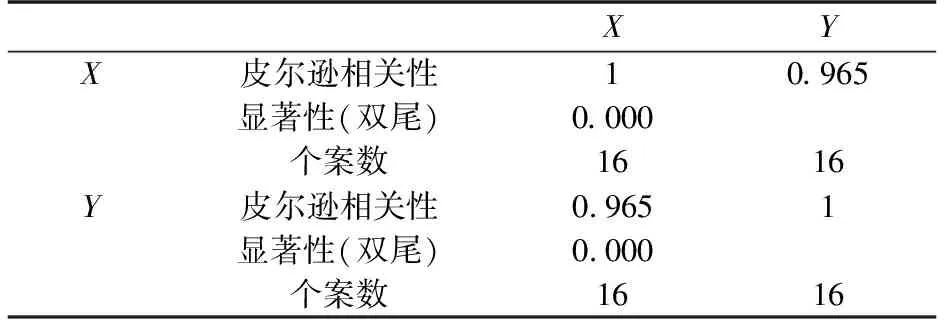
表3 迁入人口与确诊人数相关性分析Table 3 Correlation analysis of correlation between immigratingpopulation and confirmed number of people
对14 d内从武汉迁入至其余各地区的人口比例平均值与相应的累计确诊人数用统计软件SPSS进行相关性分析,结果如表3所示.
表中X表示平均迁入人口比例,Y表示累计确诊人数,从显著性水平来看:双尾显著性检验结果为0.000,说明两者之间的相关性检验通过且相关性十分显著;从皮尔逊相关系数检验结果来看:两者之间的相关系数为0.965,说明具有很强的正相关关系,即一个地区在该时间段内由武汉迁入的人口数越多,那么该地区确诊的病例就越多.
2.2.2 交通方式与确诊人数关系研究
根据收集到的湖北省内各地区航空、铁路、公路3种交通方式的连通情况,分别以各地区为网络节点、彼此相连为邻边画出3种交通方式的网络图以及度分布图发现:飞机并不是湖北省内的主要交通出行方式,其节点网络图较稀疏且度值较小;因铁路和公路的节点网络图更密集且度值都较大,所以火车和汽车为湖北省内的主要交通出行方式.
下面本文从省内3大交通方式的节点网络图以及度分布图中提取出除武汉市外其余地区的航空、铁路、公路度数据,对3大交通方式的度数据和各个地区的确诊人数之间进行相关性的分析:
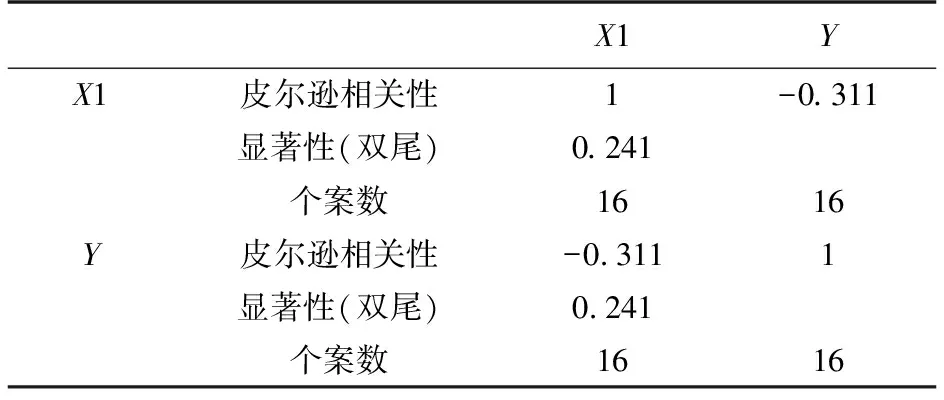
表4 航空度数据与确诊人数相关性分析Table 4 Correlation analysis of air travel dataand confirmed number of people
以上分析中X1表示航空网络度数据、X2表示铁路网络度数据、X3表示公路网络度数据. 表4显示:航空网络的度与确诊人数之间的皮尔逊相关性检验的P值为0.241,无论在0.05还是0.01水平下都不显著;表5显示铁路网络的度与确诊人数之间的皮尔逊相关系数为0.528,说明二者之间具有相关性且显著性检验通过;表6显示公路网络的度与确诊人数之间的皮尔逊相关系数为0.785,说明二者之间具有较强相关性且显著性检验也通过.
因此从3大交通方式的度与确诊人数的相关性分析比较,可以得出铁路与公路网络的度与确诊人数之间的相关性是显著的,航空网络则不显著. 此结果说明相对于航空而言铁路和公路这两种交通方式“更有利于”疫情的传播. 笔者认为导致该结论发生的原因主要有:(1)铁路和公路与航空不同的是这两者每途径一个城市就会有人流量的交换(上车与下车),这种交换越频繁就会加大疫情传播的风险且伴随发生的交叉感染也更常见. (2)人们选择铁路和公路时其路途中花费(暴露)的时间会更多,与其他人交流的可能性也更大.
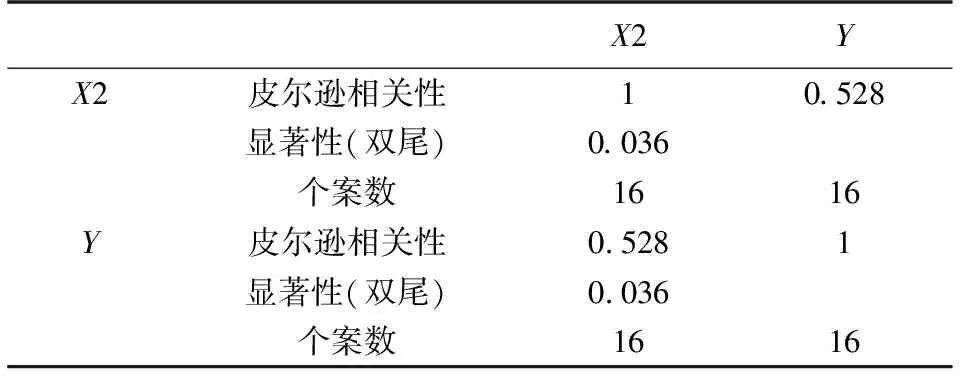
表5 铁路度数据与确诊人数相关性分析Table 5 Correlation analysis of railway degree dataand confirmed number of people

表6 公路度数据与确诊人数相关性分析Table 6 Correlation analysis of highway degree dataand confirmed number of people
2.2.3 度-度距离的城市聚类与确诊人数关系研究
基于模型(5),本文从航空、铁路、公路3层交通网络分析湖北省新冠肺炎的传播情况,由湖北省 3种交通方式的节点网络及度分布图发现不同交通方式之间相应的度存在一定差异,得到湖北各地区的总航空度为24、总铁路度为210、总公路度为184,三者比值为:0.06:0.50:0.44,本文取各层度的比值为权重因子,从表4得出确诊人数与航空网络的相关性较差,与铁路和公路的相关性较强且强度类似. 因此本文定义湖北3层交通网络的折算因子ωi(i=1,2,3)如下:
(6)
其中ωi(i=1,2,3)分别表示航空层、铁路层、公路层的折算因子. 本文交通网络中各层权重的设置主要是考虑到站点与站点之间的连接情况,即各层网络度的比值,就湖北省内的交通情况来看,目前省内的出行还是主要以铁路和公路为主,航空次之. 因此按照本文的标准来确定各层的权重比值符合现实情况;在其他多层网络权重设置中也要结合实际网络的情况,比如在经济学多层股票网络中进行权重设置时则可以考虑按照行业的分类情况进行相应的折算因子设置.
由公式(4)和模型(5)计算得到了表7中各地区之间的度-度距离与每个地区的平均度-度距离,基于表7的结果进行系统聚类分析,结果如图2所示.
对湖北省各地区按照相应的确诊人数进行系统聚类的结果如图3所示.

表7 湖北各地区之间的度-度距离Table 7 Degree-degree distance between different regions in Hubei
图2和图3中1-16的编号依次表示为:孝感、黄冈、荆州、鄂州、随州、襄阳、黄石、宜昌、荆门、咸宁、十堰、仙桃、天门、恩施、潜江、神农架.
从依据度-度距离聚类的结果来看,一共把湖北各地区分为了4类:孝感、黄冈、荆州为第一类;鄂州、随州、襄阳为第二类;黄石、宜昌、荆门、咸宁、十堰为第三类;仙桃、天门、恩施、潜江、神农架为第四类. 从基于确诊人数的聚类结果来看依旧把湖北各地区分为了Ⅳ类,孝感、黄冈为第Ⅰ类;荆州、鄂州、随州、襄阳为第Ⅱ类;黄石、宜昌、荆门、咸宁、十堰、仙桃、天门为第Ⅲ类;恩施、潜江、神农架为第Ⅳ类. 据以上可以看出基于度-度距离聚类的结果与按确诊人数的聚类结果之间的一致性很高,17个地市州排序完全一致,而且都分成了4类,只是在每一类中包含的地市州略有区别.
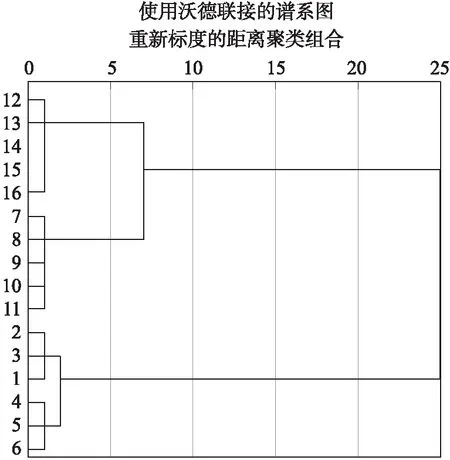
图2 基于度-度距离的聚类分析结果图Fig.2 Graph of clustering analysis results based ondegree-degree distance

图3 基于确诊人数的聚类分析结果图Fig.3 Graph of clustering analysis results based onconfirmed number of people
3 结论
本文在对新冠疫情的传播研究中,对湖北省内各地区的航空、铁路、公路3层交通网络通过构造度-度距离模型进行分析得出的主要结果如下:
(1)人口的流动与此次疫情的传播有极强的关联:从表1可以看出在研究时段内湖北省内各地区由武汉迁入的人口数越多,该地区的确诊人数也越多;
(2)湖北省内本次新冠疫情的传播在不同的交通方式中存在较大的差异:铁路和公路这两种交通方式在一定程度上“更有利于”疫情的传播;
(3)可以按照度-度距离划分“城市群”来实施层级防控:从度-度距离聚类结果可以看出度-度距离越接近的城市其疫情的严重程度也更接近,因此在疫情防范过程中可以按照这种划分更有针对性、更有效率地进行防控.
当然本文也仍需做更深的推广和探讨:
(1)文中人口的流动和交通网络的构建范围仅限于湖北省内,所有网络连接也都是在省内,可进一步推广到省外的人口流动和交通连接并对其进行分析;
(2)文中通过构建度-度距离模型来对此次疫情的传播情况进行分析时,所采用的相关病例数据均为确诊人数,可考虑对其按照卫健委标准进行细分,如确诊数、易感数、无症状感染数、死亡数.
