磁性纳米粒子的磁声谐波成像研究
2022-06-20曹睿杰郭各朴马青玉郭余庆
黄 洋,曹睿杰,郭各朴,马青玉,郭余庆,,王 军
(1.南京师范大学计算机与电子信息学院/人工智能学院,江苏 南京 210023)(2.江苏能建机电实业集团有限公司,江苏 泰州 225327)
随着纳米生物技术、医学成像技术和靶向基因/药物转染等技术的发展,生物医学成像成为靶向药物传输及早期肿瘤监测必不可少的工具[1-3]. 目前用于浅表组织成像方式主要分为两类,一是通过血流分布特征反映浅表组织病变程度,如三维能量多普勒超声成像[4]、超声造影成像[5-6]、超微血流成像技术[7-9]等;二是通过组织物理特征反映病变程度,例如剪切波弹性成像[10-11]和光声成像[12-13]. 以上两类方法具有高灵敏度、高特异度、高对比度和高分辨率等优势,但是受外界条件影响大、仪器体积庞大、价格昂贵.
磁性纳米粒子(magnetic nanoparticles,MNPs)具有独特的磁响应、良好的生物相容性和生物降解性等特点,可作为基因药物的磁性非病毒载体,利用其对机体各个病变组织部位亲和力的不同,使药物到达特定的治疗部位,在肿瘤的早期检测和治疗方面有着独特效果[14-16]. 磁性粒子成像(magnetic nanoparticles imaging,MPI)和磁感应磁声成像(magnetoacoustic tomography with magnetic induction,MAT-MI)都具有高灵敏度和高时空分辨率的优势,图像对比度较高,而且无电离辐射,因而受到了广泛关注. MPI方法由Gleich等于2005年首次提出[17],利用MNPs在磁场中的非线性响应进行成像,并利用驱动场加速零磁场点(field free point,FFP)的运动来研究了信号强度与激励频率等参数的关系. 为了优化(magnetic particle imaging,MPI)系统矩阵和提高图像的分辨率,Tay等改进了MPI的驱动激励[18],提高了磁场驱动能力和MPI的成像质量. MAT-MI将 MNPs独特的磁响应与电阻抗成像(electrical impedance tomography,EIT)的高对比度和超声成像(ultrasonic sonography,US)的高分辨率优势相结合. 2012年Hu等基于声传播理论推导了MNPs在脉冲磁场激励下的振动特性[19-20],利用时间反演算法重建MNPs的分布,实验验证了MNPs声源重建的可行性. 2016年,Mariappan等人将MNPs注射到大鼠的前列腺肿瘤中[21],利用短脉冲磁场激励和基频信号接收,重建了MNPs的分布,证明了基于MNPs的MAT-MI在软组织肿瘤成像中的应用价值. 然而利用MPI方法重建MNPs分布需要求解大型病态矩阵,或利用反卷积算法对图像进行复原,而MAT-MI方法也需要利用复杂的反演算法才能实现. 2020年Guo等人基于交变磁场激励下MNPs的机械振动,分析了磁声二次谐波的产生机理[22],利用激光测振仪测量磁声二次谐波响应,证明了磁声谐波声压与MNPs浓度的线性关系,为MNPs浓度分布的测量和成像奠定了基础. 然而,大线圈激励下无法获得MNPs振动的精确空间信息,如何利用MNPs磁声谐波响应特性实现磁声谐波成像,提高MNPs成像精度成为亟待解决的关键问题.

图1 交变磁场激励下MNPs磁声谐波响应产生和测量示意图Fig.1 Schematic diagram of the magnetoacousticharmonic response of MNPs underthe excitation of an alternating magnetic field
本文基于锥形磁芯电磁激励下MNPs的磁声谐波响应,提出了一种磁声谐波检测和成像方法. 首先利用锥形磁芯构建了具有高磁场强度和梯度的有效磁场区域,推导了交变磁场激励下MNPs的磁声谐波响应和磁声检测声压公式,理论仿真了不同模型大小和MNPs浓度的成像结果;然后研究了非理想锥尖模型的平顶高度对成像性能的影响,证明平顶高度能够有效提高磁声谐波响应和穿透深度,但扩大的有效磁场区域一定程度降低了成像精分辨率;最后利用环形坡莫合金的磁屏蔽效应进一步缩小有效磁场区域,改善了成像分辨率和对比度. 本文所提出的磁声谐波成像及其优化方法为MNPs在浅表成像中的应用提供了理论和技术支持.
1 原理和方法

(1)
(2)
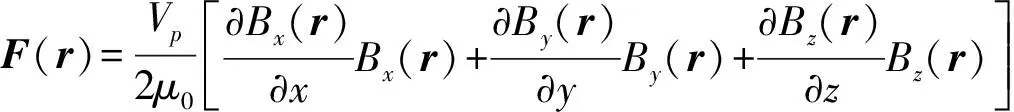
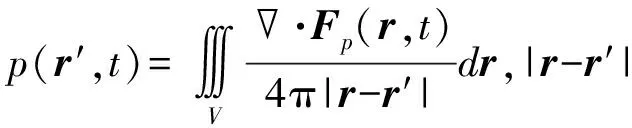
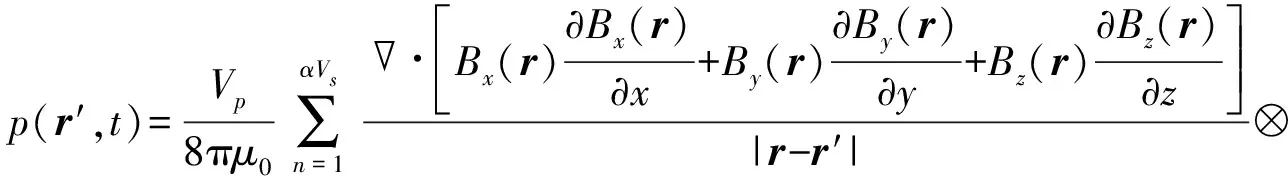
(3)
式中,⊗为卷积符号,δ(t-|r-r′|/c)引入传播距离所产生的时间差.上式表明MNPs谐波响应可以表示为溶液中所有粒子振动信号的叠加与时间项函数的卷积,可以简化为[25]:
p(r′,t)=pδ(r′,t)⊗[χ1+χ1cos(2ωt)+χ2sin(2ωt)]
(4)
式中,pδ(r′,t)为冲激电流δ(t)激励下的系统单位脉冲响应,其分布由测量系统决定,不因激励信号频率的变化而变化.因此,在交变磁场激励下,溶液中任意观测点检测到的磁声谐波声压包含直流分量和二次谐波分量,其大小由磁场分布,交变磁场的激励频率以及粒子的交流磁化率决定;当粒子数量足够多,能够抵消其离散分布对声压的影响时,检测点的声压p(r′,t)和MNPs浓度α呈现基本线性的关系,这为利用磁声谐波响应进行MNPs的浓度成像奠定了理论基础.
2 仿真与分析
为了提高交变磁场激励下MNPs磁声谐波响应声压和信噪比,采用带有锥形磁芯的线圈模型构建大磁场强度/梯度的特殊磁场,利用幅值为5.0 A,频率为4.86 kHz的连续正弦信号激励线圈,其中磁芯总高度为45 mm,半径为8 mm,磁芯顶端20 mm范围内绕制150匝线圈,磁芯锥形高度为25 mm,理想锥体的平顶高度h=0. 通过Comsol构建磁场模型,以0.01 mm进行网格剖分. MNPs溶液的粘滞系数η=8.9×10-4Pa·s,当激励信号频率为4.86 kHz时,弛豫时间τ=1.6×10-3s,直流磁化率χ0=0.58,交流磁化率χ1=2.43×10-4和χ2=1.19×10-2,利用公式(2)仿真得到MNPs溶液的冲激响应如图2(a)所示,峰值所对应的时间约为2.7 μs,与尖劈换能器接收点与锥尖的传播距离4 mm完全符合. 进而利用冲激响应卷积MNPs的传输特性,得到如图2(b)所示的MNPs谐波响应的稳定声压波形,可见波形中只存在频率为9.76 kHz的二次谐波信号,证明了MNPs的磁声二次谐波响应,同时完全相同的信号幅度可以用来进行磁声谐波声压检测和成像,具有良好的稳定性.
进一步,以理想锥体为例,当作用区域的高度为2.0 mm时,其有效半径从0到2.5 mm逐渐变大,磁声谐波声压与区域半径的关系如图2(c)所示,可见声压幅值随着区域半径的增大而增大,当半径增大超过0.7 mm时,磁场强度/梯度较弱,声压趋于平缓而到达一个稳定值,以声压最大值的95%为标准确定其有效磁场区域半径约为0.65 mm. 磁声谐波声压幅值与穿透深度的关系模拟结果如图2(d)所示,可见声压随着穿透深度的增加而降低,最后趋于0. 以声压幅值衰减到最大值的5%为标准,得到其有效磁场区域高度为1.05 mm.

图2 交变磁场激励下,MNPs溶液的(a)冲激响应和(b)磁声谐波响应声压波形,磁声谐波声压幅值与(c)有效区域半径和(d)穿透深度的关系Fig.2 Simulations of(a)the impulse response for MNPs and(b)the magnetoacoustic harmonic response excited byan alternating magnetic field,and dependences of the magnetoacoustic pressurewith respect to(c)the radius and(d)the penetration depth of EMV

图3 不同(a)组织半径和(b)粒子浓度条件下的磁声谐波声压图像及其一维声压分布Fig.3 Reconstructed images based on the magnetoacoustic harmonic response forthe models of various(a)radii and(b)concentrations of MNPs
为了实现二维MPNs浓度分布重建,构建了半径为D,高度为2 mm的圆柱体组织模型,MNPs溶液浓度为A(mg/ml),控制锥形磁芯以步进d进行二维扫描,利用换能器测量MNPs的磁声谐波响应,并利用声压幅值与粒子浓度的线性关系进行成像,得到结果如图3所示. 图3(a1)-3(a3)给出了A=30 mg/mL和d=0.2 mm时3种半径溶液模型的二维声压分布图像,沿中心轴线提取声压,得到如图3(a4)所示的一维声压分布. 可知,当锥尖位于模型边缘处,部分磁场区域包含MNPs,磁声谐波声压较小;当锥尖逐渐向溶液内部移动,包含MNPs的磁场区域越来越大,磁声谐波声压逐渐增大;当有效磁场区域都含有MNPs时,磁声谐波声压达到最大值. 模型边界处出现了由低到高的过渡带,其宽度约为1.3 mm,与有效磁声区域的直径(0.65 mm×2)相同,因此得到有效磁场区域的大小(过渡带宽度)决定了磁声谐波成像的分辨率. 然而,当模型直径小于有效磁场区域的直径时,磁声谐波响应无法达到最大值,磁声谐波声压幅值不能正确反映MNPs浓度分布的相对关系. 图3(b1)-3(b3)显示了3种浓度MNPs溶液的磁声谐波声压图像,可以看出半径约为2.5 mm,与设定的模型大小基本一致,而且随着MNPs浓度的增加,磁声谐波声压随之增大.
在本实验室的磁声谐波成像研究中,为了提高振动信号的测量灵敏度,引入激光干涉测量技术[25]进行磁声谐波振动的测量,获得了和模拟基本一致的磁声谐波波形[26],但是实验测量信号的声压幅值略大于理论仿真结果,推断可能是非理想锥尖导致. 实际磁芯制作很难实现理想锥尖,非理想锥尖可看成存在一定高度的平顶,这种非理想锥尖会对MNPs的磁声谐波响应产生较大的影响. 模拟了锥尖平顶高度h=0,2和4 mm时,xoy和yoz平面内的磁场强度分布,结果如图4所示.当磁芯为理想锥体时,磁场产生从中心向周围减弱的分布;随着锥体平顶高度的增大,xoy平面内的磁场成环形分布,圆环处磁场强度最大. 另外,如图4(a1)-(c1)所示,环形区域半径与平顶区域半径基本一致,进一步结合yoz平面的磁场分布,可以看出非理想锥尖所形成的有效磁场区域基本呈圆筒状分布.

图4 平顶高度h为(a)0,(b)2和(c)4 mm时xoy/yoz平面内的磁场强度分布Fig.4 Distributions of the magnetic field intensity in the xoy and yoz planes forthe flat heights h of(a)0,(b)2,and(c)4 mm
进一步,在保持上述电流激励条件下,对非理想锥形磁芯所形成的磁场中MNPs的磁声谐波响应进行仿真,得到不同平顶高度时的有效区域半径、声压幅值以及穿透深度,如图5所示的分布表明,随着磁芯锥尖的平顶高度的增大,磁声谐波响应幅值以及成像深度得到了大幅度提升,能够提高成像的信噪比和对比度,但是随其增大的有效磁场区域半径会在一定程度上降低图像的分辨率. 因此如何在不增大有效磁场区域半径的前提下,大幅度提升磁声响应幅度,是磁声谐波成像的关键.
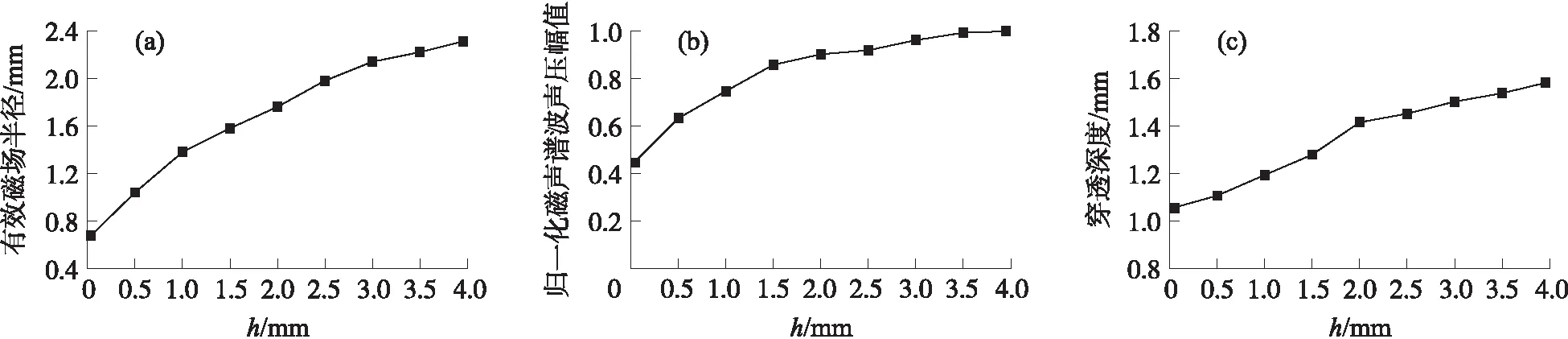
图5 平顶高度h对(a)有效磁场区域半径,(b)磁声谐波声压和(c)穿透深度的影响Fig.5 Dependences of the flat top height on(a)the radius of the effective magnetic volume,(b)the pressure and(c)the penetration depth of the magnetoacoustic harmonic response
前人研究表明,坡莫合金具有高磁导率、低矫顽力和高饱和磁化强度,具有良好的磁屏蔽功能[27-28],在非理想锥尖上安装一个环形坡莫合金磁屏蔽材料,有望进一步减小有效磁场区域的半径,优化磁声谐波成像质量. 假设所用的环形坡莫合金磁屏蔽材料的内半径为0.75 mm,外半径为5.0 mm,高度为0.2 mm,平顶高度2 mm. 仿真得到如图6(a)所示的xoy及xoz平面内的磁场分布,环形坡莫合金的引入大大约束了xoy方向的磁场半径,加快了磁场强度的衰减速度,磁场的穿透深度略有减小. 进一步,对引入环形坡莫合金后的MNPs磁声谐波响应进行数值仿真,并基于磁声谐波声压与纳米粒子浓度的线性关系得到一维磁声谐波声压分布,其结果如图6(b)所示. 同样以声压最大值的95%为标准,发现非理想锥尖模型引入环形坡莫合金后,其磁声谐波声压和穿透深度略有降低(约90%),有效磁场区域半径从1.76 mm减少至0.94 mm,证明环形坡莫合金能够基本保证磁声谐波声压不变,同时有效提高磁声谐波成像的分辨率和对比度.

图6 (a)非理想锥形磁芯模型(h=2 mm)在引入环形坡莫合金后xoy/yoz平面内的磁场强度分布,(b)不同激励条件下磁声谐波成像的一维分布Fig.6 (a)Distributions of the magnetic field intensity in the xoy and yoz planes produced by a toroidal permalloy withh=2 mm,and(b)the corresponding 1-D distributions under different excitation conditions
3 结果与讨论

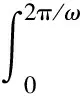
另外,影响MNP图像分辨率的因素主要包括有效磁场半径r与扫描步进d. 进一步通过改变锥尖角度为35.49°,43.60°和56.14°,在3种有效磁场区域半径条件下模拟磁声谐波信号,获得如图7(a)所示的磁声谐波成像的一维径向分布,可见随着有效磁场区域半径的增加,过渡带变宽,图像分辨率变差;另外,在锥角为35.49°时模拟了不同扫描步进条件下所获得的磁声谐波声压,重建如图7(b)所示的图像. 可见,随着扫描步进的减小,重建图像的像素点数量增加,重建图像的精度提升,但成像速度会受到一定的限制. 因此,利用锥尖的平顶和环形坡莫合金可以提高磁声谐波响应幅值,同时缩小了有效磁场区域半径,提高了成像的对比度和分辨率,但在实际应用中仍需综合考虑粒子特性,合理设计电磁激励系统来获得更好的成像质量.

图7(a) 三种锥角(35.49°,43.60°,56.14°)有效磁场区域半径(r=0.65 mm,1.2 mm,2.4 mm)条件下所重建磁声谐波图像的一维声压分布,(b)三种扫描步进条件下的磁声谐波成像图像Fig.7 (a)1-D distributions of the magnetoacoustic pressure achieved for the conical cores of three cone angles(35.49°,43.60° and 56.14°)with three radii(r=0.65 mm,1.2 mm and 2.4 mm)of the EMV,and(b)reconstructed images obtained with three scanning steps
4 结论
本文基于MNPs的磁声谐波响应提出了一种磁声检测和粒子浓度成像方法. 首先基于锥形磁芯构建了电磁激励模型,基于磁矩力学和声传播理论推导了MNPs在交变磁场激励下的磁声谐波声压表达式;进而结合实际应用,分析了非理想锥尖对磁声谐波响应的影响;最后利用环形坡莫合金的磁屏蔽效应来提高磁声谐波响应声压. 研究结果表明,非理想模型锥形磁芯平顶高度能够有效提高磁声谐波响应和穿透深度,同时增大有效磁场区域半径,然而环形坡莫合金的磁屏蔽效应能够缩小有效磁场区域半径,同时提升磁谐波声声压,提高成像分辨率和对比度,为基于MNPs的磁声谐波成像及生物医学应用提供了理论支撑.
