运算次序的交换问题
2022-06-19詹华税许文彬
詹华税,许文彬
(1.厦门理工学院数学与统计学院,福建 厦门 361024;2.集美大学理学院,福建 厦门 361021)
0 引言


1) Jessen不等式。设测度空间(X,μ)满足μ(X)=1,若f∈L1(X,μ)取值于(a,b),而ψ是(a,b)上的凸函数,那么式(1)的右边有意义,且

(1)

这2个不等式在实分析和偏微分方程研究中都发挥着重要的作用。本文综述了数学分析中的一些运算交换问题,并利用控制收敛定理证明一类退化抛物方程解的稳定性。
1 二重极限与二次极限

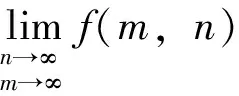
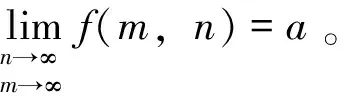

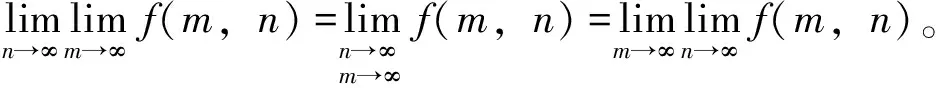
(2)


取N=max{N1,N2,N3,N4,N5},则当m,n>N时,有:
a-b=[a-f(m,n)]+ [f(m,n)-g(m)]+[g(m)-b]≤
f(m,n)-a+f(m,n)-g(m)+g(m)-b<ε/3+ε/3+ε/3=ε;
a-c=[a-f(m,n)]+[f(m,n)-h(n)]+[h(n)-c]≤
f(m,n)-a+f(m,n)-h(n)+h(n)-c<ε/3+ε/3+ε/3=ε。

2 二重积分与累次积分

(3)
(4)
要成立,式(4)的这3个积分必须都存在。
下面根据文献[4]对式(4)有关运算次序的交换分3种情况进行讨论。

以上分析说明:只要函数f(x,y)在矩形(P)=[ab;c,d]上连续,则
∂2F(x,y)/(∂x∂y)=f(x,y)=∂F(x,y)/(∂y∂x)。
(5)
此时式(4)的3个积分都存在且相等。
2)设f(x,y)在矩形(P)=[a,b;c,d]上可积,但不一定连续。如对这一函数存在一“原”函数Φ(x,y),即∂2Φ(x,y)/(∂x∂y)=f(x,y),则

(6)
这与用原函数表示通常定积分的公式相类似。



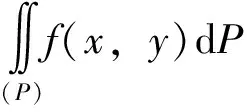



3 一类退化抛物方程解的稳定性
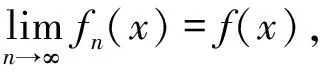
实际上可以看出,控制收敛定理就是极限运算与积分运算相互交换的问题。本节将利用控制收敛定理来探讨一类各向异性的退化抛物方程的解的稳定性。
考虑如下方程
(7)

ut=0=u0(x),x∈Ω,
(8)
和部分边界条件
u(x,t)=0,(x,t)∈∑p×(0,T),
(9)
其中,部分边界∑p⊆∂Ω的具体表达式后面再详细给出。
记


(10)
初值条件在
(11)
的意义上成立。
定义3 设u(x,t)为具有初值(8)的方程(7)的弱解。如果u在迹意义下满足部分边界条件(9),则称u(x,t)为具有初始边界条件(8)、(9)的方程(7)的弱解。
当pi(x)=pi时,方程(7)的初边值问题解的存在唯一性已由文献[14]给出,故本文在此不再重复。下面就利用控制收敛定理将文献[14]的稳定性结论推广到变指数的情形。首先来介绍一下由文献[14]所提出的弱特征函数方法。
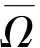

本文的主要结论是定理3。
定理3 设u(x,t)、v(x,t)为方程(6)的弱解具有初始条件u0(x),v0(x)和边界条件
u(x,t)=v(x,t)=0, (x,t)∈∑p×(0,T)
(12)
的2个解, 且弱特征函数φ(x)满足
(13)
若
bi(u,x,t)-bi(v,x,t)≤cai(x)1/pi(x)u-v,i=1,2,…,N,
(14)
则有
(15)

(16)
根据文献[15]的引理3.1,有:
(17)
同时,由pi(x)-Laplace算子的单调性,有:
(18)
由于
(19)

(20)
同时,类似于文献[14],利用部分边界条件(12)和控制收敛定理,可以得到
(21)
类似于文献[13],利用定理的条件(13)和控制收敛定理,可以得到
(22)
类似于文献[14],利用部分边界条件(12)、定理的条件(13)和控制收敛定理,可以得到
(23)
其中,r<1是个常数。
由式(16)~式(23),得到

利用推广的Gronwall不等式,有
让τ→0, 有
当然,如果选择不同的弱特征函数,部分边界条件(12)的表达式也不同,这就涉及如何选取最优部分边界条件的问题。这一问题在文献[14]中已经有了一些讨论,在此不再重复,本节所研究的内容,就是利用控制收敛定理将文献[14]的结果推广到了变指数情形。
