广义Korteweg-de Vries方程的高精度差分格式

邓雅清，王晓峰，王小利，何育宇

(闽南师范大学数学与统计学院，福建 漳州 363000)

0 引言

非线性波是应用研究的重要领域之一，目前，已有很多研究者建立了数学模型来研究非线性波动现象。Korteweg等[1]于1895年发现的KdV方程便是非线性波现象的数学模型之一。自发现KdV方程以来，人们便对这个方程及其变化形式进行了大量研究：李家永等[2]对定界的KdV方程提出一个2阶3层线性差分格式；Anjian[3]研究了具有幂律非线性和时变系数的KdV方程的孤波解；盛秀兰[4]基于Crank-Nicolson方法对KdV方程周期边界问题提出一个2层线性化隐式差分格式，其收敛阶数为O(τ+h2)；郭瑞等[5]用Crank-Nicolson差分法求解KdV浅水波方程的定解问题，并用数值模拟出孤立波这一物理现象，该法具有二阶收敛性；胡越等[6]在一定条件下证明了一类广义KdV方程行波解的存在性，但没有给出求解的方法。

本文考虑一维3阶的非线性广义KdV方程

ut+αuxxx+γ(up)x=0, (x,t)∈(-∞,+∞)×[0,T],

(1)

初值条件和边界条件分别为：

u(x,0)=u0(x),x∈(-∞,+∞),

(2)

u(-∞,t)=u(+∞,t)=0,ux(-∞,t)=ux(+∞,t)=0,t∈[0,T],

(3)

其中：α和γ是任意实数；p是大于1的正整数；u0(x)是已知的光滑函数。

非线性KdV方程(1)～(3)有2个守恒量，分别是质量Q和能量E，即：

1 高精度差分格式

(4)

(5)

(6)

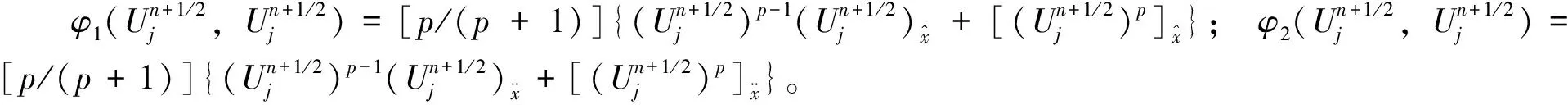
为了证明格式的稳定性，需要引理1和引理2。

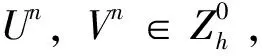
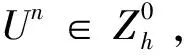
2 差分格式的守恒律

定理1 差分格式满足下列守恒性质

(7)

(8)

则分别称为质量守恒和能量守恒。

证明将差分格式(4)乘以h，作j=1到J的累加，由边界条件可得

(9)

从而质量守恒式(7)得证。

3 差分格式的可解性

为了证明差分格式(4)～(6)的近似解U1,U2,…,UN的存在性，本文将使用以下Brouwer不动点定理。

定理2 差分格式(4)～(6)的近似解Un是存在的。

(10)

4 差分格式的稳定性

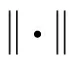
定理3 差分格式(4)～(6)是无条件稳定的。

(11)

(12)

(13)

(14)

(15)

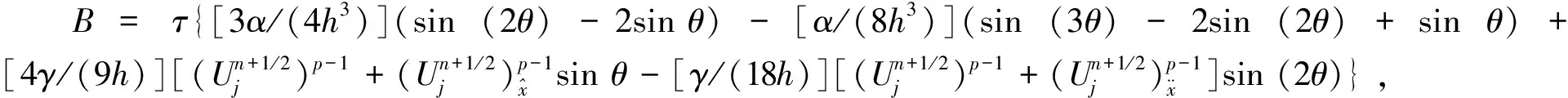
5 数值算例

算例1 取α=1,γ=3，p=2,经典KdV方程[15]：ut+uxxx+3(u2)x=0, (x,t)∈[xL,xR]×[0,T],设方程初值条件为：u0(x)=0.5sech2(0.5x),则该方程的精确解为：u(x,t)=0.5sech2[0.5(x-t)]。

图1表明，差分格式(4)～(6)的数值解与精确解具有很好的吻合。为了验证差分格式的质量和能量守恒，表1给出了xL=-20、xR=60和不同h、T时Qn、En的值。

表1 守恒量式(7)和式(8)的数值模拟

表1验证了差分格式的质量和能量的守恒性。为了验证差分格式的收敛精度，表2给出了xL=-40、xR=100、T=60时不同h、τ下的误差和空间收敛阶，表3给出了xL=-20、xR=60、T=10、h=1/100时不同τ下的误差和时间收敛阶。

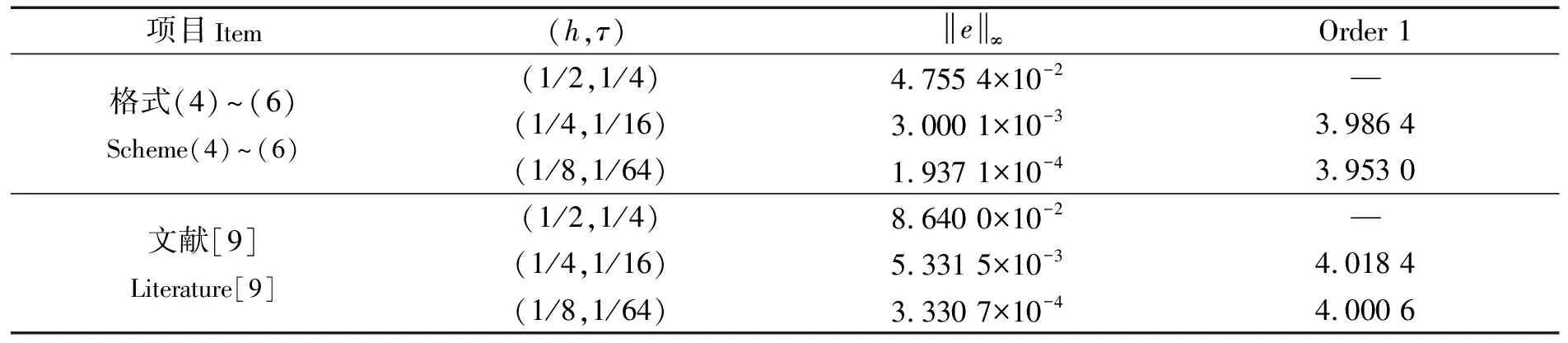
表2 不同步长下的误差和空间收敛阶

表3 不同τ下的误差和时间收敛阶

表2验证了差分格式在空间上具有4阶，表3验证了差分格式在时间上具有2阶的收敛精度。该结果与前面的理论推导部分结果一致。

文献[15]中格式(19)是一个4阶3层线性差分格式，由表2可以看出，差分格式(4)的误差比文献[15]中格式(19)的误差更小。

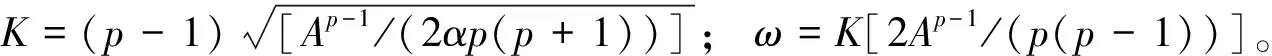
取A=0.8，x0=10，固定XL=-20，XR=60，h=0.5，τ=h2，p取不同值时在不同时刻的数值模拟波形图见图2，数值模拟网格图见图3。

由算例1和算例2可以看出，本文针对初边值问题(1)～(3)所提的差分格式(4)～(6)是有效的。

图4给出了p=2和p=3的2个数值孤立波碰撞的俯视图。图5模拟了p=3的2个数值孤立波在T=0～200区间内的碰撞。可见，碰撞前高的波追赶小的波，碰撞后两个波能很好地分离，随后两个波均保持形状不变地向前运动。