锥阀典型面密封结构空化喘振数值仿真研究
2022-06-18刘禹明
刘 钊, 刘禹明, 陆 亮, 孙 波
(同济大学 机械与能源工程学院, 上海 200092)
引言
空化现象普遍发生于包括锥阀在内的各类控制阀口,导致流量饱和、溃灭噪声、微射流气蚀等严重问题[1]。经典的节流阀口空化模型认为阀口高速流动形成流束收缩,压力降低,内部气核在低于饱和蒸汽压的条件下成长,并流动至下游高压处溃灭[2]。
空化过程多发生于湍流中,较为复杂,湍流相关研究多采用CFD的方式,以定性研究中多采用RANS时均湍流模型。如GAO Q等[3]通过k-ε湍流模型对大流量高速开关阀流场进行了数值计算仿真,结果表明,流道内形成涡流从主流中提取能量,增强了流体噪声。FILO G[4]团队根据CFD模拟的结果修改了止回阀的几何形状,新设计的压力损失显着降低。
关于锥阀空化的研究,基于时均湍流的RANS模型也占据了主导地位,包括HAN M等[5]对3种典型锥阀结构进行数值计算,分析得出二级节流阀(TS阀)能有效抑制气蚀的发生,但在一定程度上也增加了阀口的阻力损失。谢海波等[6]通过CFD仿真得到不同阀座结构对锥阀液动力方向大小均有影响的结论。RUNDO M等[7-8]通过CFD仿真对锥阀的液动力计算公式进行了评估,发现在某些操作条件下,逆流分析公式与 CFD 模拟结果之间存在显著差异,后针对锥阀几何形状对流量-压力特性的影响进行了研究,提出了一种可以准确预测锥阀流量压力特性的模型。NIKANDISH P等[9]的研究表明,增加锥角和阀芯的位移,通过阀门的油流的最大速度将会降低。
实际上,伴随可视化技术的发展[10],研究者们越来越清晰的发现旋涡流动形成空化的特点,如ZHU J等[11]对文丘里管空化的研究。但目前基于RANS湍流模型的空化仿真无法清楚的描述流场中的剧烈旋涡流动。
近期,基于旋涡空化的认知,不少研究者们开始大胆尝试使用DNS模型或LES等经过较少简化的湍流模型,比如LU L等[12]基于LES模型复现了滑阀U形阀口的固定旋涡空化。YUAN C等[13]基于准DNS(quasi-DNS)方法提出了锥阀线密封结构旋涡导致空化的特点,并详细分析了其伴随结构和流动参数变化的规律。而锥阀面密封结构的阀口空化特性不同于线密封,且空化与其导致的喘振现象更为明显。
随着针对锥阀空化研究的进行,锥阀的振动问题凸显了出来,如袁聪等[14]对锥阀的空化形态进行了很好的复现,并观察到了空化喘振的现象。刘兆领等[15]针对某一内缩型平衡阀(结构类似锥阀),通过理论和数值仿真分析,得到空化气穴受入口压力、开度影响,且得出气化噪声强弱与气穴大小无关的结论。闵为等[16]通过流固耦合模型进行锥阀振动分析,其模型虽然将阀芯弹簧考虑在内但仍观察到了空化作用对阀芯振动的影响。针对类似问题也有很多学者将重点放在减弱空化上,如王银等[17]利用优化设计方法对锥阀某些参数以减小空化为目标进行优化,数值计算结果表明优化后空化确有减弱。
基于此,本研究在建立LES空化仿真模型基础上,以锥阀面密封结构为主要对象,代表性的分析了面密封锥阀旋涡空化成形规律,并对其导致的喘振现象进行细致分析,包括背压和锥阀开度变化对喘振特性的影响,分析旋涡空化喘振的规律。
1 仿真数学模型
1.1 结构性网格生成与独立性分析
开度为1 mm、阀座母线为2 mm的锥阀面密封结构的计算流域可以被简化成图1a中的回转体流域,其余结构类似。此流域相比全流域结构已经简化了很多,但是为了划分出更高质量的网格,仍需进一步简化。考虑到简化后的流域为旋转结构,故可进一步化简成二维流域,简化后的流域如图1b所示,可以支持划分高质量的网格并大幅减小计算量。

图1 面密封锥阀流域简化Fig.1 Simplified flow area of surface-sealed poppet valve
本研究采用 LES 湍流模型进行动态仿真,需要高质量的网格,因此选用结构性网格。结构性网格灵活性较差且划分方式复杂。但是结构性网格质量高,同样网格尺寸下数量更少因此计算更快,如边界层等位置更能迎合流场方向。
最终将计算流域划分成6个四边形块,如图2所示。这种划分方式的优点是越接近空化发生流域网格也越密,而且网格方向与流场方向基本一致。
通过指出四边形块上每个边含有的节点数,可以将其分割成更小的微元体。相邻块的共同边上的节点数相同。节点在边上默认均匀分布,但LES湍流模型不会对近壁面网格做特殊处理,因此需要更细的近壁面网格,设置最小壁边界层为1 um,增长率为1.05。由于空化发生流域处流场比较复杂,所以空化发生流域处(块3和4)拥有更多的节点和更高的网格密度。

图2 网格分块Fig.2 Grid blocking
通过商业软件ICEM进行网格独立性分析,生成5种密度条件的结构化网格,如表1所示。块3和块4始终具有最大网格密度,网格数量较大,体积占用较小。对5种工况的网格质量均进行改进以符合计算条件,关键参数如表2所示。

表1 块内网格数Tab.1 Number of grids in a block
为进行网格独立性分析,首先比较相同阀门压力和配置下5种网格密度条件的时均流量情况,如图3所示。可以发现, 网格1和其他网格之间出现了较大的差异,而网格4和网格5之间的流量值接近。因此,似乎没有必要将网格密度从网格4增加到网格5,换句话说,使用网格4条件,数值计算结果将独立于网格的划分及密度。

图3 网格独立性分析Fig.3 Grid independence analysis
图4显示了所选Grid 4条件的整个流域的网格细节,可以发现空化发生流域中的网格是密集生成的。对于LES中的近壁处理,表示无量纲壁距的关键y+数小于1。

图4 空化发生流域与边界层网格细节Fig.4 Mesh details of cavitation flow domain and boundary layer

表2 网格质量参数Tab.2 Mesh quality parameters
1.2 物理模型与边界条件
LES湍流模型通过边界条件计算出大尺度的涡,并根据耗散率计算小尺度的涡,与RANS将一切参数在时间上平均的方法相比,LES可以获得更多的流场细节特征和动态行为。LES模型多用于三维模型计算,而面密封锥阀流域沿阀锥高度对称,几乎无周向速度梯度,ANSYS Fluent中对此类轴对称物理模型可使用二维简化计算,其中二维旋流的切向动量方程可以写成:
(1)
式中,r—— 对称轴的径向坐标
ρ—— 流体密度
μ—— 动力黏度
t—— 时间
u,v,w—— 分别为轴向、径向、切向速度分量
多相流模型使用Mixture模型,基于Euler-Euler方法,将不同的相当作空间上混合在一起的连续相。计算混合相的动量方程和第二相的相对速度,典型应用包括空泡流、粒子沉降等。在Mixture模型中,两相具有相同的速度和压力分量,质量和动量守恒可以表示成:
(2)
(3)
式中,vm—— 质量平均速度
αk,vdr,k—— 分别为第k相的体积分数与漂移速度
F—— 外力
n—— 总相数
p—— 压力
其中,下标(i,j,k)表示笛卡尔坐标系的方向。混合相的密度ρm和混合相的动力黏度μm被定义为:
ρm=ρlαl+ρvαv
(4)
μm=μlαl+μvαv
(5)
式中,α为体积分数,下标v,l分别表示蒸汽相和液相。
空化模型基于这样一个物理假设:液体中含有气核并在低压下成长形成空穴。其用来建模常温下压强低于饱和蒸汽压时液体破裂出现空泡的过程。Schnerr-Sauer模型使用蒸汽体积分数的表示方式,需要指定的参数少,计算稳定性和收敛性好。因此本研究选择 Schnerr-Sauer模型建模空化过程。
Schnerr-sauer模型中的质量输运方程为:
(6)
其中,v为速度,源项Re,Rc分别表示气泡的生长和破裂:
p (7) p>pv (8) 空泡直径Rb与空泡密度N有关,可表示为: (9) 求解算法采用基于压力的耦合(Coupled)算法。尽管耦合算法需要花费更长的时间用于计算,但是可以获得更精确的速度和压力值。求解过程是在商业CFD软件Fluent上完成,详细的仿真设置如表3所示。 表3 数值计算求解设置Tab.3 Calculation settings 本研究涉及的液压系统认为蓄能器和溢流阀使得测试阀入口处压力恒定,测试阀出口压力由靠近油箱的节流元件决定。节流元件前压力由开度和系统流量决定,当节流阀开度一定时,由于锥阀的空化现象与系统流量耦合在一起,导致系统流量波动,因此节流元件压力也随着波动。在测试阀的仿真中,出口压力通过UDF定义。测试阀的出口流量如方程式(10)所示: (10) 其中,pout—— 测试阀的出口压力 pa—— 油箱压力 Cd,A—— 分别是流量系数和节流阀的节流面积 通过方程变换,pout可以进一步表示为方程式(11): (11) 出口边界条件为瞬态压力的 UDF 逻辑框图如图5所示。 图5 瞬态压力出口边界的UDF设置Fig.5 UDF settings for outlet pressure 其中,F_UDMI是一个用户自定义的存储空间(UDM,User defined memory),用来存储和读取出口变量。F_FLUX 是一个宏函数,可以获得流过单元边界的流量。通过常数出口压力初始化流场后,出口单元边界处的流量通过F_UDMI获得,求和得到整体出口流量后使用方程式(17)计算并设置出口边界压力,最后进行整体流场计算。流域时刻拥有一个恒定的入口压力边界条件以及每一步都不同的出口压力边界条件。对于每一次迭代,到达预设的迭代次数(Ite>50)或达到收敛条件(Res<1e-6)后,当前时间步计算完成。然后将出口边界处的流量值保存到F_UDMI内,开启下一时间步的计算。 为了验证仿真结果的合理性,对与网格结构相同的结构进行实验,保持阀前压力3 MPa,改变阀后压力,时均流量对比结果如图6所示,ε为仿真结果相对实验计算的误差值。可以看到,实验结果和仿真结果基本一致,仿真误差ε不超过10%。这表明仿真模型合理可靠,可以代替实验对滑阀空化喘振进行更深入的研究。 图6 仿真与实验时均流量对比Fig.6 Comparison of average flow between simulation and experiment 首先讨论空化形成的机理,设置锥阀开度为1 mm、入口压力3.0 MPa、出口节流元件CdA值为12e-6 m2/s对其进行数值计算得到结果如图7所示。 图7a中白色的空泡产生于阀口的面密封壁面处,对比数值计算压力分布结果如图7b,可以看出空化空穴位置与低压区位置匹配,空化由低压产生。伯努利原理告诉我们,流场中流速越快压力越低,然而观察图7c中流场流线计算结果,喉部的小灰度高流速区域与图7b中的低压区并不完全匹配,反而是贴近壁面的区域压力较低。进一步放大观察图7d中的喉部流线,发现贴近壁面区域产生了速度较低的旋涡结构与图7b中的低压区高度一致,从而可以推出,面密封锥阀阀口处由于流束内收缩在壁面产生了旋涡结构,旋涡结构导致局部低压产生空化。 图7 仿真结果图Fig.7 Simulation results 空化喘振指阀口空化剧烈程度周期性变化, 并和周围流域耦合,导致系统压力流量随时间波动的现象。图8是一组锥阀内有代表性的空化喘振过程。图中用方块形点标记了空穴末端位置,根据观察到的空穴图像,喘振过程主要在空穴截面长度上延伸和缩短。因为空化喘振是系统层面的振荡特性,阀入口流量、出口流量和出口压力也同样会振荡,如图9所示。根据图5的UDF,出口流量和出口压力同时计算,故图9中两者同步。同时可以看到入口流量波动幅度远小于入口流量波动幅度。入口流量、空穴体积、出口流量三者遵循如下规律: (1) 当阀口处流量增大,会引起流速增加压强降低,于是空穴体积增大堵塞阀口,又引起流速减小压强升高,如此循环往复。这解释了持续性流量脉动的机理。 (2) 蒸汽密度远低于油液密度,当空穴体积缩小时,油液会填充原来由蒸汽占据的空间,于是流向下游的油液减少,出口流量减小;当空穴体积增大时,蒸汽会占据原来由油液占据的体积,于是流向下游的油液增多,出口流量增大。这解释了出口流量比入口流量有更大幅值的原因。但是入口流量和出口流量具有相同的时均值。 (3) 在相位上,空穴体积变化速度领先于出口流量,出口流量略领先于出口压力。这是因为空穴体积改变时,直接影响出口流量,出口流量改变后出口压力经后续节流元件反馈随之改变。 如图8和图9所示, 可以看到一个明显的喘振过程,空穴体积周期性的增加和减小,引起流场参数随之波动。为了获得频域特性, 对其做快速傅里叶变换(FFT),得到图10。可以看到一个频率在5000 Hz附近的峰值,这就是空化喘振频率。 图8 典型的空化喘振行为Fig.8 Typical cavitation surge behavior 图9 时域上的流场特性Fig.9 Flow characteristics in time domain 图10 频域上的流场特性Fig.10 Flow characteristics in frequency domain 图11则定义了4个监测点,进一步展示了空穴内部的动态压力波动,如图12所示,将时域信号转为频域见图13。可见,4个点的压力波动有相同的周期特性,且越远离槽入口,波动幅值也越大。这种区别很容易解释,因为4个监控点在位置上沿着流动方向,槽口入口压力是恒定的,但是出口压力随着流量波动。具体来说,p1,p2,p3处在阀口空化处,展现涡流引起的负压力(见图12左侧坐标轴)。其中越远离阀口波动幅度越大,压力越高,表示靠近阀口处空化较为固定,而远离阀口处产生较为剧烈的空化生成与脱落过程。而p4处于非空化区域,仅展现较强的压力波动(见图12右侧坐标轴),因压力较高故没有空化现象。 图11 p1~p4位置定义Fig.11 p1~p4 position definition 图12 p1~p4处压力时域变化Fig.12 Time-domain variation of pressure at p1~p4 图13 p1~p4处压力频域变化Fig.13 Frequency-domain variation of pressure at p1~p4 1) 不同背压下的喘振行为 图14分别展示了不同背压下的出口流量。需要注意的是,在前文中已经提到背压是通过UDF定义的,通过改变CdA值即节流阀开度可以改变背压大小(由于背压是动态变化的,因此此处的背压是时均值)。为了强调不同背压下的不同,在图14中的出口流量以均值为中心展示,不同曲线纵坐标尺度不同。流量曲线在均值附近展现了不同程度的喘振。同样的,对其做傅里叶变换后得到图15,其中较高背压(CdA值较低)下的入口流量在频域上具有相似的峰值频率,约为 5000 Hz,而较低背压下的出口流量在5000 Hz左右有多峰值分布,源于背压低到一定程度离散气泡较多且大小不一,下游离散气泡溃灭对流量的影响较严重。不同背压下的喘振具有不同的幅值,表现为背压越低,振动幅值越大,这也源于背压越低时空化现象越剧烈的特性。 图14 不同背压下锥阀出口流量时域特性Fig.14 Time-domain outlet flow characteristics of poppet valve under different back pressures 图15 不同背压下锥阀出口流量频域特性Fig.15 Frequency-domain outlet flow characteristics of poppet valve under different back pressures 2) 不同锥阀开度下的喘振行为 因为面密封结构锥阀空化多发生在密封区域,所以密封区域的结构尺寸对空化将有重要影响,理解两者关系将有助于提出抑制空化喘振行为的措施。下面首先讨论不同开度Lo下的空化喘振行为,同时保持其他条件不变,锥阀阀口开度定义如图16所示。 取出口压力时域频域特性如图17、图18。开度从1 mm增加到1.5 mm时主频减小,幅值减小。当开度从1 mm减小到0.5 mm时幅值减小的同时主频升高至18500 Hz附近。这是由于开度减小,流量减小但流速增加,出入口压力条件一致的情况下空化更为严重。即当空穴减小后阀口处低压旋涡发育更快,空穴增大更快,所以开度越小,频率越高。而流量波动幅度与空穴体积变化相关,空穴越小,空穴体积变化越小,出口流量幅值变化也就越小。当开度从1.0 mm减小至0.5 mm时空化加剧但空穴体积减小,而当开度从1.0 mm增大至1.5 mm时空化减弱空穴体积减小,所以出现了幅值随开度先增大后减小的现象。 图16 面密封锥阀阀口开度定义Fig.16 Dimensions of face-sealed poppet notch 图17 不同开度下锥阀出口流量时域特性Fig.17 Time-domain outlet flowrate characteristics under different opening 图18 不同开度下锥阀出口流量频域特性Fig.18 Frequency-domain outlet flowrate characteristics under different opening 基于此结论,笔者团队已申请专利[18],通过在锥阀阀后设置刚度可变蓄能装置用于削弱空化喘振对系统的不利影响。通过对当前开度喘振频率与幅值进行预测,计算得到合适的刚度参数设置于蓄能装置以达到最佳的喘振消除效果。 本研究基于LES湍流模型、mixture多相流模型与Schnerr-Sauer空化模型,对锥阀面密封结构旋涡空化成形机理及其喘振行为机制进行了仿真研究,研究结果表明: (1) 在阀芯与阀座密封处形成大尺度空穴,涡流在大尺度蒸汽空穴的生成过程中扮演着重要角色。油液流过密封区域流束内收缩,与阀座壁面处形成固定旋涡,固定旋涡导致局部低压致使油液气化形成空穴,空穴附着于壁面; (2) 空化喘振是一种系统固有的不稳定性,和流场参数耦合在一起,形成持续性的振荡现象。在相位上,出口流量落后于蒸汽体积变化速度,入口流量又落后于出口流量,入口流量和出口流量的时均值相同。在喘振过程中,主要是液体-蒸汽之间的传质过程。空化空穴具有动态性,在空穴上游油液气化为蒸汽运动到空穴下游再液化为油液。这种动态性造成了空穴的膨胀和收缩,并影响系统流量; (3) 对比分析了背压和锥阀开度对空化喘振的影响。背压对喘振频率影响不大,但过低的背压产生的下游气泡会使喘振频率成分复杂化。背压越小幅值越大。锥阀开度会影响空化发育速度与空穴尺度,开度越小,空化发育速度越快,空穴越小,但过大的开度也会因流速减小导致空穴减小甚至消失。空化发育速度越快喘振频率越高。空穴越大,喘振幅值越大。依此结论设置阀后蓄能装置可实现更好的喘振削弱效果。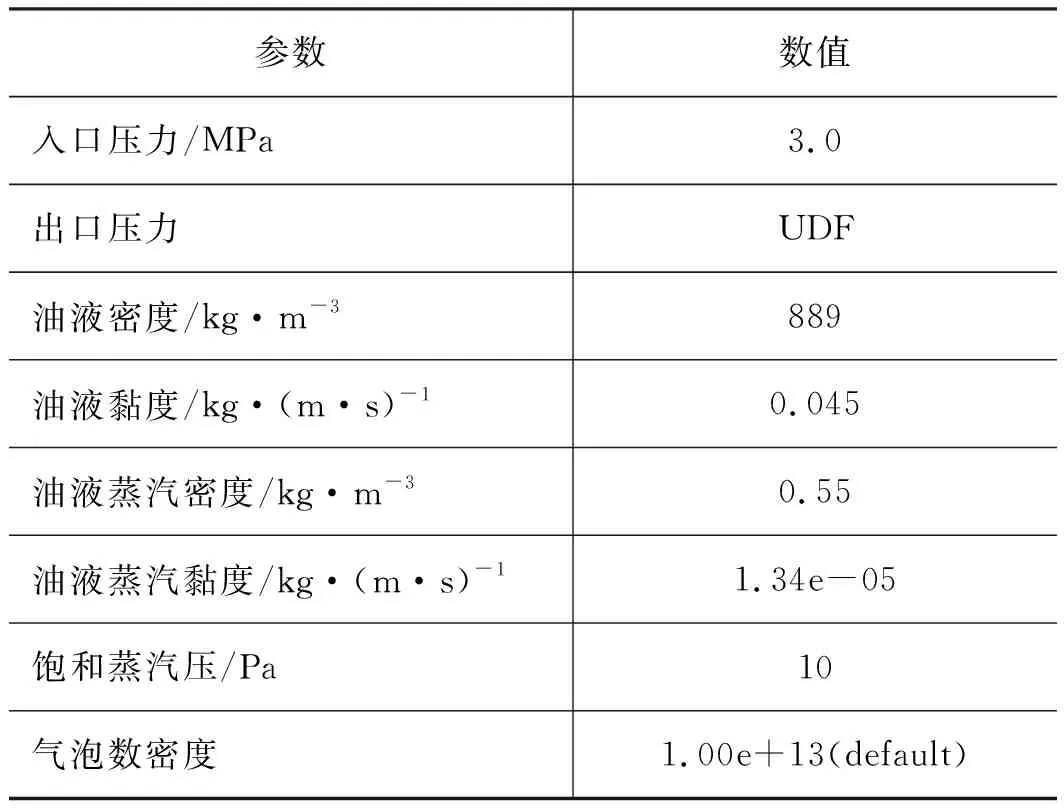

1.3 仿真模型合理性验证

2 空化喘振行为及机理
2.1 旋涡空化成形机理

2.2 空化喘振下的流场参数振荡特性






2.3 背压和锥阀开度对空化喘振的影响





3 结论
