具有双边时延和丢包的无时间戳网络控制系统的状态镇定①
2022-06-17吴兴臣
吴兴臣 刘 斌 胡 勇
(*武汉科技大学冶金自动化与检测技术教育部工程研究中心 武汉430081)
(**湖北省冶金过程系统科学重点实验室 武汉430081)
(***北京控制工程研究所 北京100190)
0 引言
网络控制系统(networked control system,NCS)因其有着布线少、效率高、灵活性与可靠性高,且简化了系统的安装和维护等优点,成为了国内外众多学者的研究热点[1]。同时NCS 在复杂工业领域的工程控制、现代交通领域、基于信息网络的运动控制系统(如无人机、智能车),以及运输领域内的协调控制(公路车辆调度、飞机控制调度)等各种控制领域中具有广泛的应用前景[2]。但是网络控制系统也存在一些不可忽视的问题。由于信息是通过通讯网络进行传输,所以网络带宽的限制、负载的数量、控制系统各传感器、执行器、控制器等节点工作方式的不同都会对系统产生不同程度的影响。同时在网络传输过程中,各式各样的数据不可避免地会发生排队等候与碰撞丢失,导致产生了网络阻塞、时延,数据包乱序及丢失等现象,这些都会导致控制系统的性能降低,甚至不稳定。因此,考虑具有时延、丢包等数据传输异常现象下NCS 的稳定性问题成为了目前主要的研究方向[3]。
近年来,许多学者从不同角度对NCS 的设计问题进行了研究。当数据包带有时间戳时,系统可根据时间戳信息进行控制器参数及观测器参数设计[4]。然而,当数据不带有时间戳时,由于网络通道中数据传输的随机性,几乎不可能去预测时延以及丢包的详细信息。近年来有学者提出用伯努利随机变量和具有条件概率的马尔可夫过程来描述随机发生的时延及丢包,使得具有随机时延、丢包的网络控制系统变得易于分析[5-6]。
针对NCS 中存在时延或丢包的情形,文献[7]研究了网络攻击导致丢包的智能电网状态估计问题,在数据包带有时间戳的前提下分析了网络攻击导致数据丢失的特性,并设计了滤波器实时对丢失的数据进行补偿,基于改进的无迹卡尔曼滤波得到了非线性系统的实时动态状态估计值。针对同时存在时延和丢包的情况,文献[8]用一组伯努利分布随机变量描述传感器到滤波器的时延和丢包现象,在无时间戳的情况下,基于Riccati 差分方程和Lyapunov 差分方程得到了最小方差意义下的最优线性滤波器的解,并给出了稳态滤波器存在的充分条件。文献[9]在带有时间戳的前提下提出了一种基于预测的Luenberger 观测器,根据没有丢包的时刻计算当前以及未来一段时间的估计值,并基于Lyapunov函数推导了相应的观测器及冗余控制器设计方法。文献[10]考虑了一个具有丢包及其他约束条件的鲁棒网络控制系统,引入一组伯努利随机变量序列来描述具有丢包上限的不确定性系统,并设计了一种鲁棒滤波器来补偿丢包造成的影响。文献[11]将系统建模为具有伯努利随机分布变量的状态空间模型,提出了一种具有固定攻击周期导致系统丢包的干扰模型,同时考虑系统的固有丢包,研究了网络干扰攻击下的信息物理系统的状态反馈稳定问题。文献[12]研究了一类在反馈信道和前向信道中存在网络诱导时延和数据包丢失的离散网络控制系统的有限时间镇定问题,利用预测控制方法,提出了一种新的有限时间状态反馈和输出反馈镇定控制器,可对时延和数据包丢失进行主动补偿,并在有限时间内使系统稳定。
针对网络控制系统存在时延、丢包等传输异常的问题,现在已经有了大量的研究,但目前的文献大多未综合考虑多方面的问题,存在一定的局限性。如文献[4]、[6]、[10]中均要求数据包带有时间戳,使得估计器与控制器可以根据时延及丢包的情况预测并在线计算估计值与控制量。文献[9]、[11]、[13]只考虑存在时延或丢包的情况,文献[7]和[8]只考虑了单边存在时延和丢包的情况。实际网络控制系统中的传输机制错综复杂,需要考虑如何建立前向通道及反馈通道同时存在数据传输异常现象的系统模型,以及后续的观测器及控制器设计问题。
基于以上情况,本文考虑一类双边存在时延和丢包的无时间戳网络控制系统的状态观测器及控制器的设计。首先,引入两组伯努利随机分布变量来描述前向通道和反馈通道存在随机时延和丢包的特性,其中数据包不带有时间戳,并通过增广矩阵的方式建立系统模型。基于Lyapunov 函数以及线性矩阵不等式方法分析系统的稳定性,得到了系统稳定的充分条件,最后通过仿真实验验证了方法的有效性。
1 问题描述及系统模型建立
本文考虑一类存在时延与丢包的网络控制系统(如图1),传感器将系统输出y(k) 通过网络通道传送给观测器,观测器接收得到具有时延和丢包的输出数据(k),并通过分析得到系统的状态观测值(k),控制器计算状态观测值得到控制量(k),并通过网络通道传送至执行器,执行器接收得到具有时延和丢包的数据u(k)。其中,随机网络时延和丢包存在于前向通道(控制器-执行器)与反馈通道(传感器-观测器)中。传感器、控制器与执行器均为时间驱动,传感器采样周期为T。
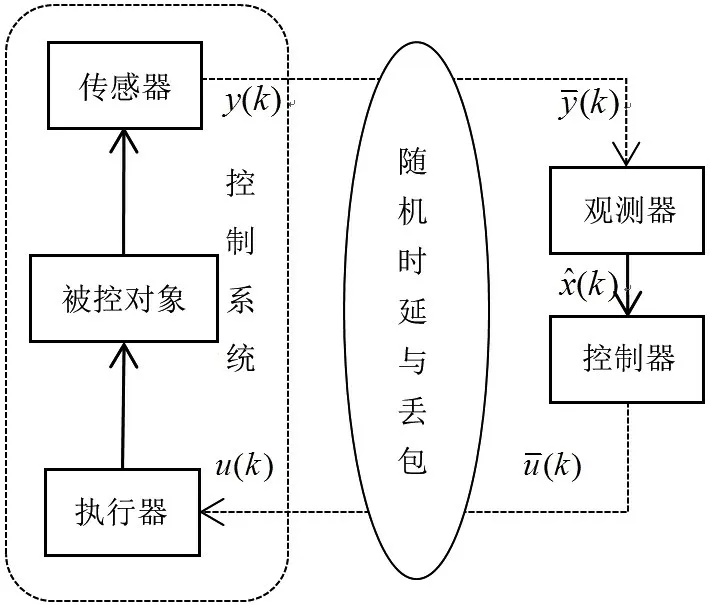
图1 具有双边随机时延与丢包的系统模型
本文中,Rn和Rm×n分别表示n维和m×n维实欧几里德空间;给定向量ω∈Rn,‖ω‖ 代表欧几里得范数;Z+代表正整数集;I和0 分别表示具有适当维数的单位矩阵和零矩阵;Pr[·]表示随机事件发生的概率;E[·]表示随机变量的数学期望;对于矩阵A,[A]T表示A的转置矩阵;λmax(A) 和λmin(A) 分别表示A的最大特征值和最小特征值;A>0 和A<0 分别表示矩阵A正定和负定;矩阵中的符号*表示对称项。
设网络控制系统的状态空间模型如下:

其中,x(k)∈Rn是系统状态,y(k)∈Rp是系统输出,u(k) ∈Rm是系统输入。A∈Rn×n,B∈Rn×m,C∈Rp×n是已知的合适维度的矩阵。在传感器-观测器通道以及控制器-执行器通道中,节点驱动方式采用时间驱动,因此数据包时延为采样周期整数倍,且假定时延上限为d。
针对系统中存在的不确定性时延及丢包,本文采用两组伯努利随机分布变量来描述具有随机时延及丢包的数据传输特性。定义两组独立不相关的伯努利随机变量分别表示k时刻反馈通道与前向通道中的数据包传输的不确定性:

其中,i=0,1,2,…,d表示k时刻接收值的延时周期数;j=1,2 分别代表反馈通道与前向通道;∈[0,1]已知,表示延时概率。表示延时i个采样周期,观测器与执行器接收到传输值的概率为表示延时i个采样周期,观测器与执行器未接收到传输值的概率为1。
在网络控制系统之中,携带时间戳的数据包由于其自身的信息通常处理较为方便,但在带宽有限的情况下,往往数据会不携带数据包从而缓解传输压力。本文中数据未携带时间戳,故只知道数据分布的先验概率,即式(2),假设数据携带时间戳,则每个时刻的伯努利随机变量(k) 已知。
根据以上定义,现以反馈通道为例,假设系统中存在随机时延及丢包,此时观测器接收系统输出值模型可通过引入上述一组伯努利变量,表示为

式(3)描述了网络系统中可能存在的有界延迟和多个丢包现象。设置时延上限d=2,表1 可表示反馈通道中(k) 取值与观测器接收数据值的关系。

表1 反馈通道数据包传输表
从表1 可知,根据每个时刻(k) 取值的不同,观测器接收值y(k)不同,其中y(1)、y(3)、y(8)和y(9)正常传输,y(4)延时一步传输,y(2)延时两步传输,y(5)、y(6)和y(7)数据包丢失。
同理,执行器接收的控制量u(k)模型可引入上述另一组伯努利变量,表示为
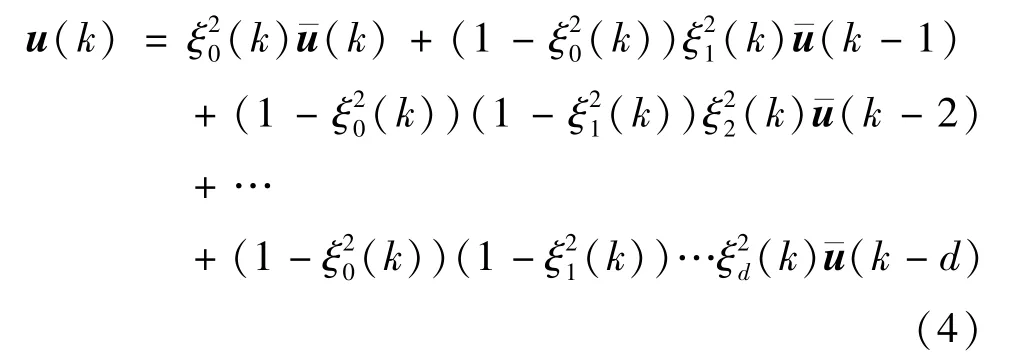
具有双边随机时延与丢包的网络控制系统(如图1 中虚线框中所示)可描述如下:

将式(3)和式(4)转化为
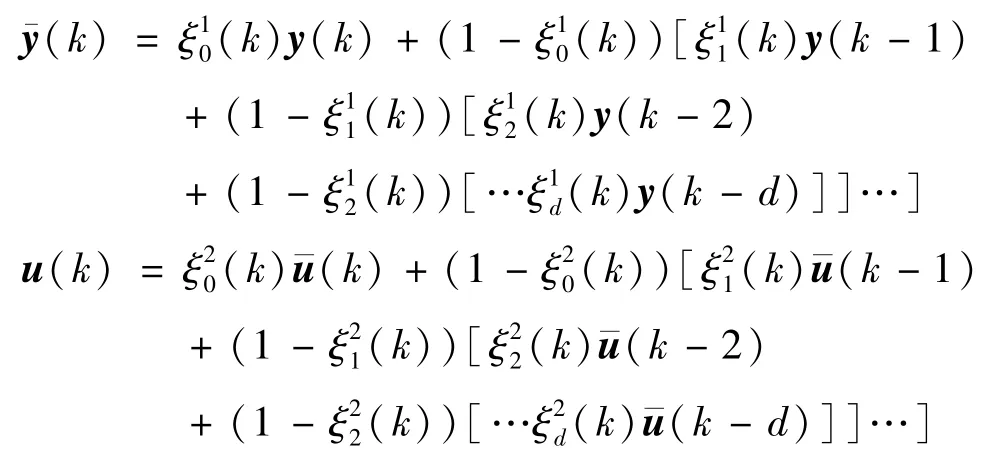
上式可转化为

其中i=0,1,2,…,d -1;zi(k)∈Rp;φi(k)∈Rm;zi(k)、φi(k) 分别表示观测器与执行器接收到经过i个采样周期时延之后的k时刻数据值。
将状态增广为

式(5)中所描述的具有双边随机时延与丢包的网络控制系统可重构为


2 系统稳定性分析
为了实现控制目标,设计式(12)中的观测器与式(13)中的控制器。

定义观测误差如下:

联立式(12)和(13),系统式(11)可改写为
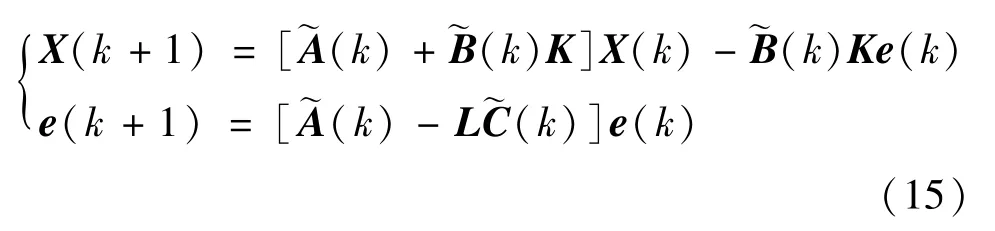
由于系统式(15)是随机参数系统,因此引入均方指数稳定性的概念。
定义1定义η(k)=[XT(k)eT(k)]T,对于系统式(15),当满足以下条件时,是均方指数稳定的。

其中,η(0) ∈Rn,k∈Z+,β >0,α∈(0,1)。
同时,根据文献[13],有以下引理1、引理2 和引理3 成立。
引理 1对于给定的李雅普诺夫函数V(η(k)),当存在ω >0,0<λ <1,υ >0 使得满足ω‖η(k)‖2≤V(η(k)) ≤υ‖η(k)‖2,E{V(η(k))| η(k -1)}<λV(η(0)),可得到:

引理3对于全列秩的矩阵B,存在奇异值分解(singular value decomposition,SVD)如下:

其中,U∈R(n+m)×(n+m),V∈Rm×m是正交矩阵,∑=diag{w1,w2,…,wm},其中wi(i=1,2,…,m)是矩阵B的非零奇异值,矩阵U1∈R(n+m)×m,U2∈R(n+m)×n。
定理1考虑存在双边随机时延和丢包的网络控制系统式(15),给定控制器增益矩阵K和观测器增益矩阵L,如果存在对称正定矩阵P和Q满足以下矩阵不等式,则系统式(15)是均方指数稳定的。

证明定义η(k)=[XT(k)eT(k)]T,针对系统式(15)构建Lyapunov 函数为
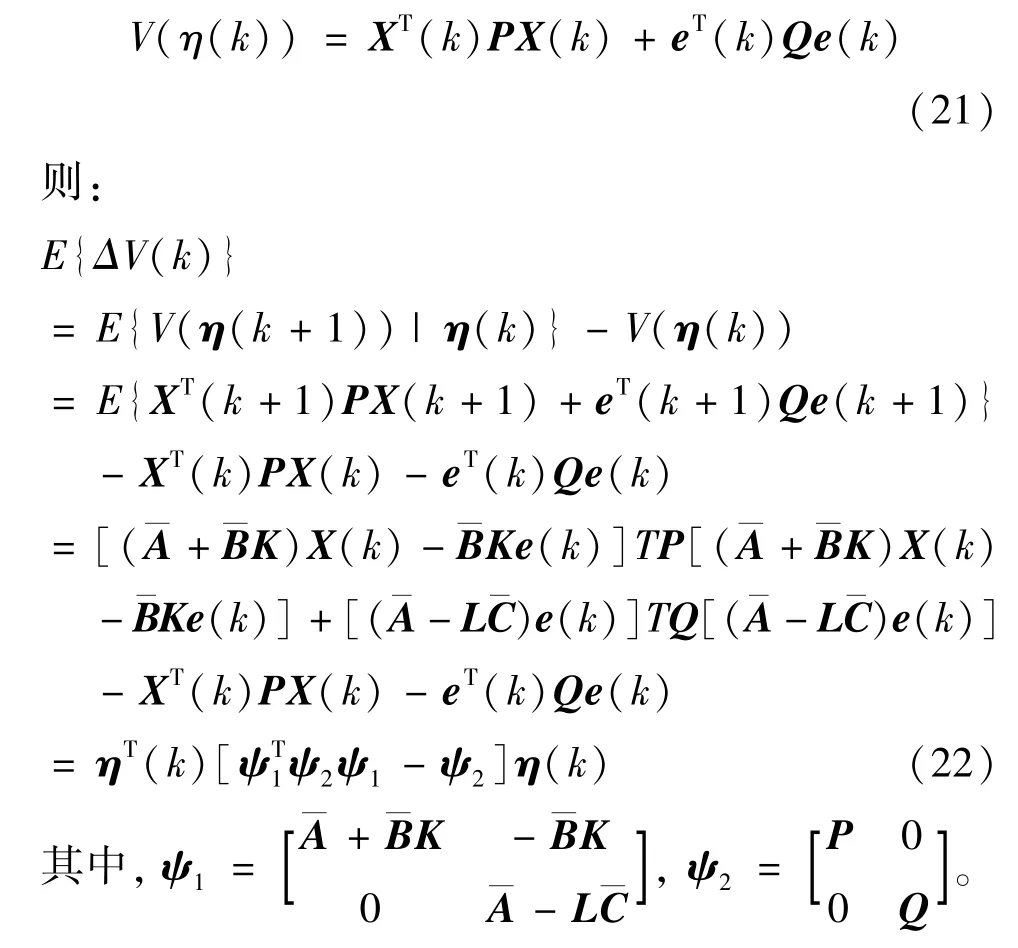
式(20)左右各乘矩阵diag{I,I,P-1,Q-1} 可得到:

令a=max{a0,a1,…,ak-1},则有:

综上,在定理1 中的不等式(20)条件成立时,系统式(15)均方指数稳定。
3 系统观测器及控制器参数设计
虽然定理1 得到了系统的稳定性条件,但是矩阵不等式(20)带有非线性项,不能用线性矩阵不等式的方法求解,本文使用奇异值分解法将不等式中的非线性项进行线性化处理,从而得到标准的LMI形式。
定理2考虑存在双边随机时延和丢包的网络控制系统式(15),如果存在对称正定矩阵P和Q以及矩阵X、Y和ˉP、P1、P2满足以下矩阵不等式,则系统是均方指数稳定的。同时,控制器增益矩阵K和观测器增益矩阵L满足式(31)。
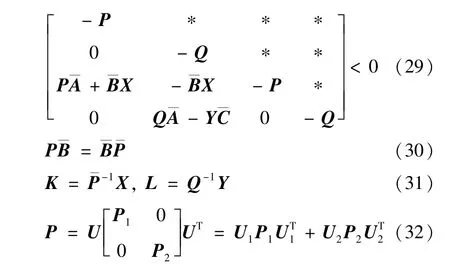
证明根据引理3 与式(30)可得:

将式(32)带入(33)可得:
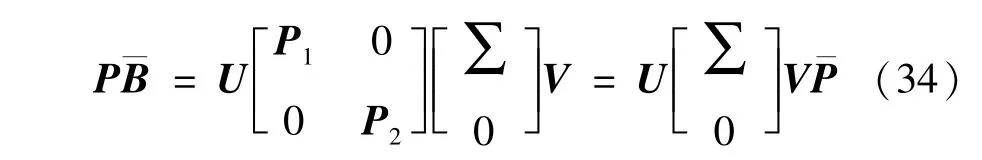
由式(34)可得:

根据式(35)可得:

因此,控制器和观测器参数如下:

将(30)、(31)带入式(29)中,可得到不等式(20),满足定理1,系统均方指数稳定。
4 数值仿真
考虑一个开环临界稳定的二阶离散系统:

实验1在系统式(38)中引入上限为d=2 的随机时延与随机丢包,设定反馈通道时延分别为0、1、2 个采样周期时接收到传输值的概率为,前向通道时延分别为0、1、2 个采样周期时接收到传输值的概率为
根据定理1 和定理2 提出观测器和控制器设计方法,通过求解线性矩阵不等式(29),可以得到如下控制器和观测器参数。

此时系统状态响应曲线与观测误差曲线如图2所示。
图2(a)给出了系统状态响应曲线,图2(b)给出了系统状态估计误差曲线。

图2 系统状态响应曲线与估计误差曲线
实验2设定反馈通道时延分别为0、1、2 个采样周期时接收到传输值的概率参数分别为,前向通道时延分别为0、1、2 个采样周期时接收到传输值的概率参数分别为
实验2 中的传输概率设定条件,相对实验1 中的设定,随机时延与丢包概率增大。通过求解线性矩阵不等式(29)可得到控制器和观测器参数:

此时系统状态响应曲线与观测误差曲线如图3所示。
图3(a)给出了系统状态响应曲线,图3(b)给出了系统状态估计误差曲线。通过实验1 和实验2对比可知,当系统时延及丢包概率增大时,状态响应曲线超调量有所增加,且收敛速度变慢。

图3 系统状态响应曲线与估计误差曲线
实验3设定反馈通道参数=1,前向通道参数,此时系统时延为2 倍采样周期的定时延,此时系统状态响应曲线如图4 所示。
由图4 可得,对于系统式(38),所能容忍最大的时延上限为d=2,此时状态响应临界稳定。

图4 系统状态响应曲线(时延为2 倍采样周期)

实验4在系统式(39)中设定反馈通道时延分别为0、1、2 个采样周期时接收到传输值的概率为,前向通道时延分别为0、1、2个采样周期时接收到传输值的概率为。此时相当于无时延及丢包现象,通过求解线性矩阵不等式(29),可以得到如下控制器和观测器参数。

此时系统状态响应曲线与观测误差曲线如图5所示。

图5 系统状态响应曲线与估计误差曲线
图5(a)给出了系统状态响应曲线,图5(b)给出了系统状态估计误差曲线。由图可知,当不存在时延和丢包时,所设计的控制器及观测器可使系统稳定。
实验5现引入上限为d=2 的随机时延与随机丢包,设定反馈通道时延分别为0、1、2 个采样周期时接收到传输值的概率为=0.3,前向通道时延分别为0、1、2 个采样周期时接收到传输值的概率为0.4。
根据定理1 和定理2 提出观测器和控制器设计方法,通过求解线性矩阵不等式(29),可以得到如下控制器和观测器参数。

此时系统状态响应曲线如图6 所示。

图6 系统状态响应曲线
图6 给出了系统状态响应曲线,说明了当前时延及丢包参数设定下,系统不稳定。针对不同的被控对象,本文方法适用的时延及丢包上限不同。
从以上的仿真结果可知,考虑具有双边随机时延与丢包的网络控制系统,采用本文所提出的建模方法及控制策略,在一定的时延及丢包上限范围内,可以使系统状态估计误差收敛,且系统状态响应能较快地收敛到稳定状态。
5 结论
本文对存在双边随机时延与丢包网络控制系统的控制器及观测器进行设计。首先,引入两组随机分布的伯努利变量对网络控制系统进行建模,描述了系统中存在的有界时延与丢包现象,通过引入新的状态变量构造了一个具有随机参数的增广系统。之后对增广系统进行李雅普诺夫稳定性分析,得到了系统均方指数稳定的充分条件,并通过线性矩阵不等式方法设计了观测器与控制器参数。最后通过仿真实验证明了该方法的有效性。与其他的网络控制系统相比,该方法更具一般性,可得到保证系统稳定的观测器与状态反馈控制器。
