需求响应型公交车辆调度及路径优化

管德永，吴晓芳，赵 杰，王 珏

(1.山东科技大学 交通学院，山东 青岛 266000；2.南京市城市与交通规划设计研究院股份公司山东分公司，山东 青岛 266000；3.青岛真情巴士集团有限公司，山东 青岛 266400)

0 引言

当前城市化进程发展迅速，居民出行OD发生经常性变化，传统公交很难快速适应[1]，很多公交线路过长，沿线公交停靠站较多，同时沿线部分公交站点乘客数量不均[2]，公交系统资源没有得到充分利用，发展新型交通模式愈加迫切。城市中居民多以中短距离出行为主，出租车灵活性高，但运载量较小；地铁运载量大，却不够灵活。城市公交系统具有覆盖面广、运载量大、灵活性高等特点[3]，因此应结合城市已有公交系统，实现车辆根据乘客的需求灵活设置停靠站点和行驶路径，使其具备更高的灵活性。

需求响应公交是根据收集乘客在客户端发出的请求，为出行起终点、出行时间等相似的乘客提供专门出行服务[4]的灵活性公交。具体特性仍为“公交”性，采用固定站点、完全不固定线路，为片区内市民提供的一种可实时呼叫或预约，系统实时聚合匹配，实时生成动态线路的新型公共出行服务。其介于私家车和传统公交之间的新型服务特性，能够满足乘客多样化出行要求，尤其是高品质出行要求，转变部分私家车出行的交通出行方式，改为公交出行。深圳、北京、西安等城市开始推行该公交模式，注册用户不断增加，获得了市场认可[5]。但准时性差、运营成本高[6]等问题不断涌现，在部分站点、路网较全，人口量少的城市区域，甚至遇到了线路遭冷落、上座率不高、报名线路人数不够无法开设等困境[7]。因此，深入研究需求响应公交的调度与优化，提升需求响应公交的服务水平具有重要意义。

Nourbakhsh[8]等对低密度需求矩形区域内发车间隔、线路设置进行了研究。Huang等[9]提出了一种动态插入方法来处理动态阶段的模型，综合了运营商与乘客的动态决策过程，解决了低需求区域的乘客出行需求。韩霜等[10]建立的基于改进遗传算法的调度决策模型能够生成数量最少且覆盖区域内所有高概率点的线路。在车辆路径优化问题中，王正武等[11-12]设计了双遗传算法，对同时接送模式下的需求响应型车辆调度优化进行了试验对比分析，相对于单独接/送模式，同时接送模式在车座利用率、成本节约方面具体更好的优越性。鲁春燕[13]为解决遗传算法搜索效率不高的难题，提出了一种基于局部优化的遗传算法，在解决问题时并未考虑到较为复杂的带时间窗的路径优化问题。赖元文等[14]设计模拟退火-自适应布谷鸟算法，改善寻优过程中跳出局部最优解而全局寻优的能力，结果表明通过模型计算出的结果均优于现有调度方案。

综上所述，现有研究对于乘客需求的响应往往是依靠经验确定，存在主观性，缺少定量研究[15]，部分研究一般假设系统只运行单辆公交，同一需求点乘客具有相同的出行需求，且车辆容量无限大[16]，研究情境过于理想化，尚未考虑我国实际道路网结构，忽略了乘客出行个性化时间窗要求[17]。

因此，本研究通过对站点历史乘车请求频次提取出高概率点，对乘客需求时空分布和出发地与目的地(OD)分析，提出在车容量、乘客需求时间约束下的二阶段需求响应型公交车辆调度及路径优化模型，先生成能够覆盖所有高概率站点的静态车辆调度决策，后生成能够满足实时预约需求的动态优化路径。

1 模型构建

1.1 问题描述

本研究将需求响应公交的服务模式抽象为多车辆从固定车场出发，依次经过各个具有时间约束的需求点，运行途中系统每隔固定时间对车辆调度方案进行更新，并回到车场的最短路径规划问题。需求点包含上下车站点，根据该区数据实际情况，将上车需求频次大于60次的站点定义为高概率上车站点，下车需求频次大于60次的站点定义为高概率下车站点。

1.2 问题假设

为便于建模，做出如下假设:

(1)各个站点最多有1个请求，若1个站点同时具有多个请求，在模型中将其拆分为地理位置相同的多个站点。

(2)每辆车任务的始发与结束都发生在配送中心。

(3)任意站点间的行驶距离为站点间的最短行驶距离。

(4)默认乘客在站点处等待。

(5)每辆车到达需求点的时刻为开始服务的时刻。

(6)不考虑道路拥堵情况，车辆平均行驶速度相同。

该模型主要的约束条件是乘客时间和车容量。参照每个站点的服务人数、时间属性，建立数学模型进行求解。

目标函数为：

(1)

式中，D为车辆总运行里程；dij为站点间最短行驶距离；i和j为需求站点；N为所有需求站点集合，表示为车辆总运行里程最小。

约束条件为：

(2)

式中，alij和aljk为0-1决策变量，若车辆l从站点i(j)开往站点j(k)取1，否则取0；dmax为初始线路允许的最大行驶距离；L为所有公交车辆集合；约束条件表述为公交初始行驶路径不能超过最大距离，所有需求站点必须被公交车辆覆盖，驶入j站和驶离j站的车辆数相等。

(3)

式中，0为车场；al0j和ali0为0-1决策变量，表示车辆从车场出发并最终回到车场。

(4)

alij∈{0,1},∀l∈N,j∈N，

(5)

式中，M为每车初始线路允许开行的最大站点数，表示经停的初始站点数量不超过M，决策变量取值约束为0或1。

1.3 车辆动态路径优化模型

车辆动态路径优化阶段，每辆车可响应周边实时乘车请求。以里程变化最小为目标，决策变量为每辆车经过各站点顺序，到达、出发时刻，建立模型求解。

目标函数为：

(6)

式中，d为总运行里程；dl为第l辆车的运行里程。

约束条件为：

(7)

(8)

N(s),

(9)

式中，N(m)为车辆必经站点集合；N(s)为车辆可选站点集合；j，k，h为需求站点；xjk，xkh为0-1决策变量；式(7)表示车辆必须访问必经站点；式(8)表示车辆可以访问可选站点；式(9)表示车辆访问中间站点后必须离开。

(10)

(11)

式中，F(j)上车站点j对应的下车站点；N(m+)为车辆必经上车站点；N(m-)为车辆必经下车站点；N(s+)为车辆可选上车站点；N(s-)为车辆可选下车站点；tj为车辆进入站点j的时间；t(s)为车辆每次启/停时间；xij和xkF(j)为0-1决策变量；tjF(j)为从站点j到站点j对应下车站点的行程时间，tF(j)为车辆进入站点j对应下车站点的时间。式(10)表示车辆若访问了上车站点j，则必须访问其对应的下车站点F(j)；式(11)表示车辆必须先访问上车站点才能访问其对应的下车站点。

(12)

(13)

xij∈{0,1},∀i,j∈N(m)∪N(s)，

(14)

2 算法设计

2.1 两阶段调度优化模型算法流程

算法包括静态车辆调度和动态路径优化二阶段。其中静态调度是一个线性整数规划模型，本研究基于LNS策略的遗传算法进行求解，采用破坏、修复算子，提升求解质量，主体框架与传统遗传算法类似。动态路径优化采取精确规划算法，将获得的动态需求插入到初始路径中，不断更新路径，图1为二阶段调度优化流程。

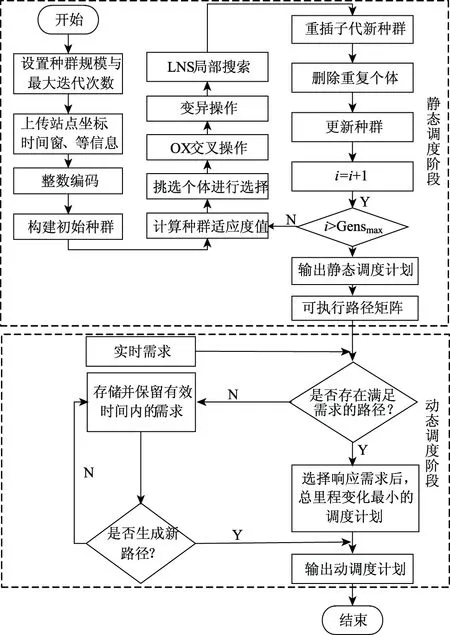
图1 二阶段调度优化流程Fig.1 Process of 2-stage scheduling optimization

2.2 算法说明

(1)编码

需求响应型公交的初始线路是由多个站点按照一定顺序排列成的，1,2,…,n表示服务区域内的高概率上车站点，其对应下车站点采用n+1,n+2,…,2n进行编号。染色体采用整数编码，当站点数为N，最大使用车辆数为L时，染色体长度为(N+L-1)，且N+1,N+2,…,N+l-1将站点数划分为3段，即产生L条运行路线，如图2所示。

图2 车辆线路编码示意图Fig.2 Schematic diagram of vehicle line code

(2)初始种群

初始种群的质量将影响遗传算法的搜索效率，为提高初始种群中的染色体质量并保证种群多样性，采用以下方法生成初始种群中的染色体。

Step 1：随机扰乱高概率出行OD对的排列顺序。

Step 3：选择下一对高概率OD，以插入后运行距离变化量最小为原则将其插入第l(l=1,2,…,l1)辆车的经停路径，判断是否满足车容量约束和乘客时间窗约束，如果满足则调整该车辆的初始路径，否则将该高概率出行点对插入下一辆车的经停路径，不断重复上述过程，直至找到满足约束的最佳插入位置。

Step 4：依次选择余下的高概率出行OD对，重复Step 3直至将所有高概率出行点对都插入车辆的初始路径中。

(3)适应度函数

为保证各条配送路径都可满足车容量及乘客时间窗约束，使用惩罚函数f(l)进行求解，由于相较于违反容量约束更容易违反时间窗约束，因此将违反容量约束权重α设为10，违反时间窗约束权重β设为100，因目标函数越小越好，将适应度函数设为惩罚函数的倒数，即1/f(l)。惩罚函数公式为：

f(l)=D(l)+αq(l)+βw(l)，

(15)

式中，f(l)为惩罚函数；D(l)为车辆l的总运行里程；q(l)为车辆l违反的容量约束；w(l)为车辆l违反时间约束的乘客之和。适应度函数为惩罚函数倒数。

(4)LNS局部搜索操作

LNS局部搜索采用破坏算子通过相似性计算公式，从当前解移除若干顾客，再使用修复算子，在满足车容量约束和顾客时间约束下，将被移除的顾客重新插回到使车辆行驶距离增加最少的位置中，具体操作步骤如下。

Step 1：对初始解(12345)使用破坏算子，将初始解中的几个相似站点(3和5)进行移除，剩下的站点(124)依旧按照初始顺序排序。

Step 2：使用修复算子对移除后的解(124)进行修复，即将移除的2个站点(3和5)随机选择1个站点，在满足约束的条件下重新插回124中。

Step 3：将生成的可能解(1234，1243，1324)进行比较，并从中选择1个最优的解，如(1243)，然后再将5插入到1243中，将生成的新解(51243，15243，12543，12435)进行比较，并从中选择1个最好的解，作为当前解，直至找到最优解。

3 案例分析

3.1 算法描述

采用MATLAB编程，对某区9月份的11 909条请求数据进行测试，通过分析该区动态巴士出行时空规律，共提取乘客该月内28 d早8:00的232条数据，对其出行OD分析获得48 个需求站点，通过对站点间最短路距离的测量，得到站点间距离矩阵，研究区域站点分布见图3。将车场定为第1个坐标点，坐标点1～48为乘客站点，车辆最大座位数为28，车辆平均行驶速度为25 km/h，乘客上下车时间1 s/人[18]，车辆起停时间2 s/次，车辆允许初始行驶路径长度20 km，车辆运行成本18 元/km，违反最大载客量惩罚系数为10，违反时间窗约束惩罚系数为100。

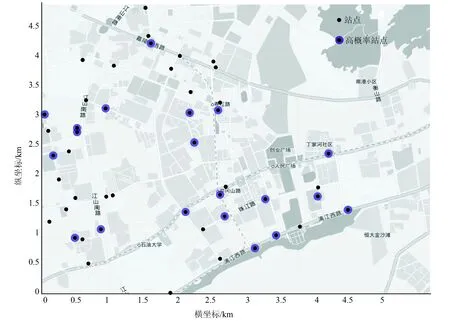
图3 研究区域站点分布图Fig.3 Station distribution in study area

3.2 有效性试验

为验证算法的有效性，对需求进行静态车辆调度，设置初始种群规模为100，交叉概率pc=0.9，变异概率pm=0.05，最大迭代次数为200。从图4可以看出，迭代次数为100 次左右时，得到最优解并进入收敛状态。

图4 迭代次数Fig.4 Iteration times

算法连续3 次得到的最优解结果如表1所示，结果偏差为3.1%，在可接受范围内，试验结果表明，该算法对问题求解的稳定性较好。

表1 最优解结果Tab.1 Optimal solution result

3.3 高概率点提取策略有效性分析

从48 个需求站点中，根据需求频率选取20 个高概率需求点，针对区域内高概率需求站点进行车辆静态调度，各高概率站点编号及其经纬度如表2所示。

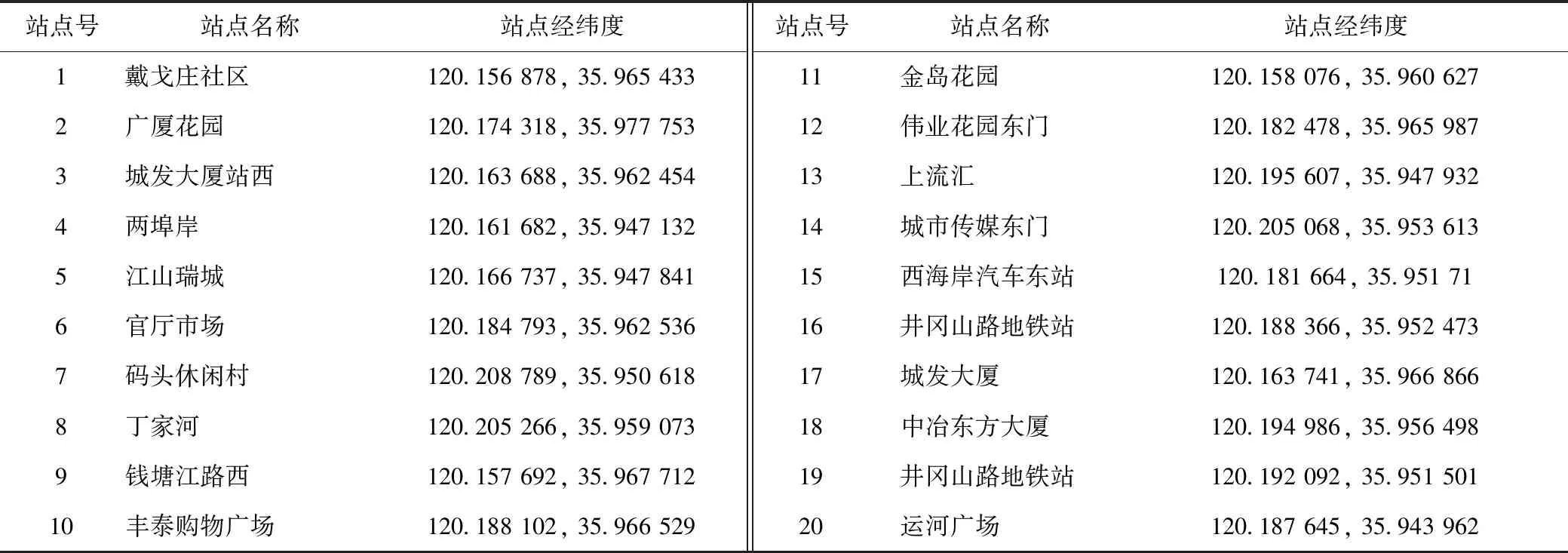
表2 高概率出行站点编号及经纬度Tab.2 Number，latitude and longitude of high probability travel stations

设置迭代次数为200，种群规模100，对比是否采用提取高概率站点策略的迭代(图5)和最优路径(图6)，看出采用策略的总成本更小，可以较少车辆满足大部分需求。

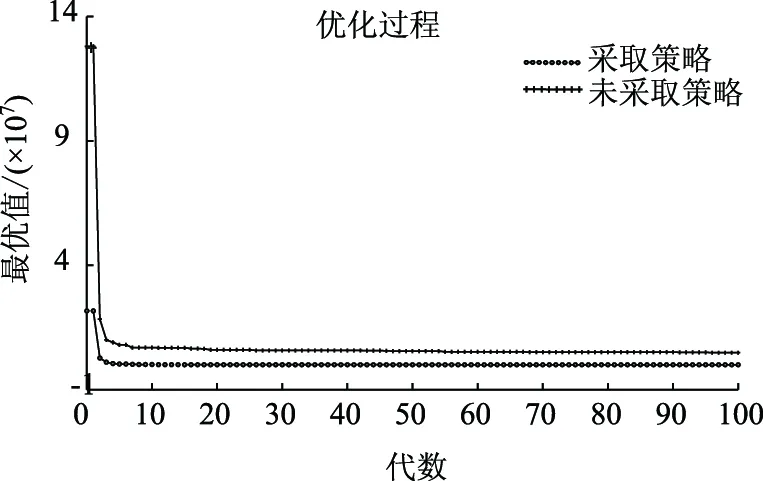
图5 有无策略迭代Fig.5 Iteration with or without strategy

图6 有无策略最优路径图Fig.6 Optimal path with/without strategy

从表3分析出，运行车辆采取该策略与未采取策略的平均总成本分别为1.04×104元和4.38×106元。结果表明，高概率点提取策略对路径优化及乘客时间节省影响明显。

表3 高概率点策略对比结果Tab.3 Comparison of high probability point strategies

平均候车时间为所有乘客发出请求时间与所请求车辆到达站点时间差的均值，表达式为：

(16)

选取该次调度结果中的5条线路，其静态调度方案见表4，乘客平均候车时间为5.4 min。分析该区测试数据中该5条线路的历史运营信息，得出乘客平均候车时间为6.23 min，为传统公交乘客平均候车时间。乘客平均候车时间缩短13.4%。

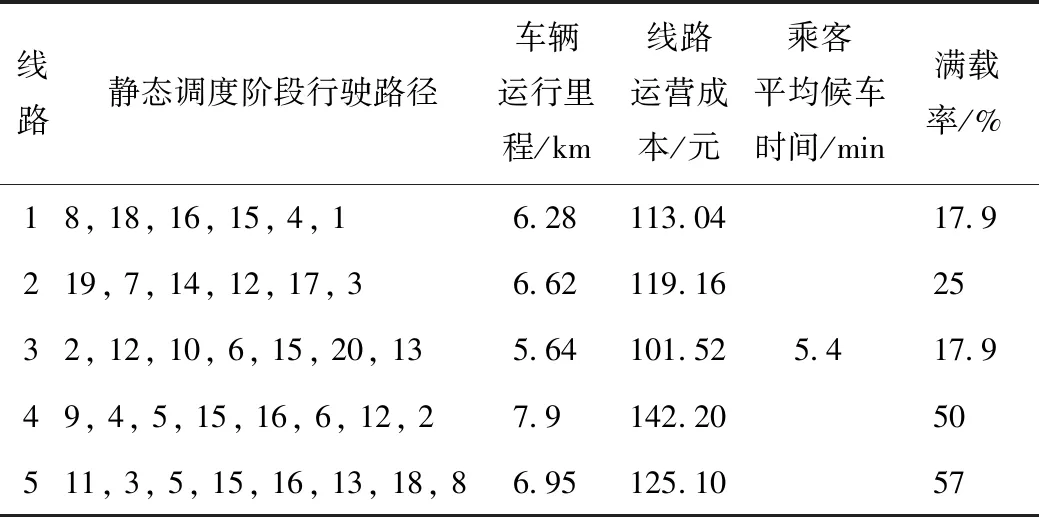
表4 静态阶段调度方案Tab.4 Static stage scheduling scheme

静态调度完成后，将生成的路径存入可执行调度计划矩阵中，为动态优化提供调用策略。

3.4 动态路径优化分析

分3个时段统计车辆运行中8:05:00—8:20:00产生的49 个随机出行需求，将其OD插入可执行调度计划矩阵中，利用精确动态规划算法进行第1轮动态优化，所得车辆运行路线见图8。

公交平均行程时间为所有乘客在车上时间的均值，包含停车时间，表达式为：

(17)

式中，T为公交平均行程时间；Q为乘客总数；q为各乘客；tqs为乘客q上车时刻；tqd为乘客q的下车时刻。

分析该区域内所对应5条线路的历史运营数据，统计分析得乘客的平均行程时间为23 min，为传统公交乘客平均行程时间。第2阶段优化后动态阶段调度方案见表5，线路2共响应12 位乘客的实时需求，搭载乘客19 人，未响应乘客数1 人，对应公交车辆运行线路由19，7，14，12，17，3更为19，7，14，12，17，3，4。其中被响应的乘客平均行程时间20.6 min，乘客平均行程时间缩短10.4%。

表5 动态阶段调度方案Tab.5 Dynamic stage scheduling scheme

如表6所示，该路径优化模型响应乘客需求率高，车辆满载率提升17.92%，运营成本变动合理，人均成本减少1.08元，节省了公司运营成本，提升了乘客满意度，得到了较好的结果。

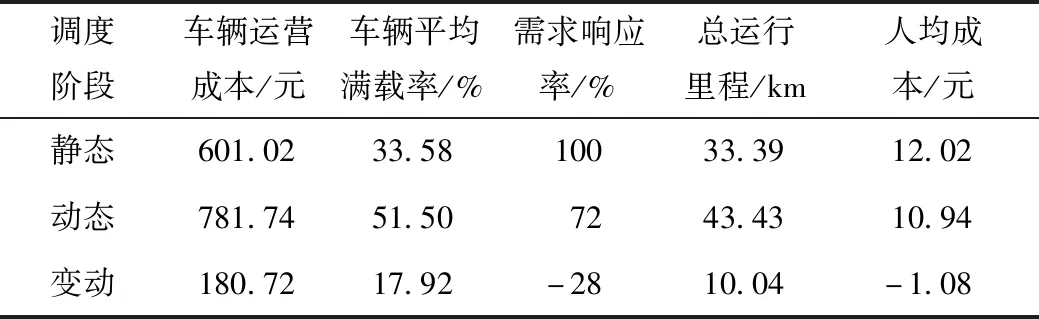
表6 两阶段调度结果分析Tab.6 Analysis of 2-stage scheduling result

4 结论

建立了二阶段模型来研究需求响应型公交的运营决策，包含2个阶段：车辆静态调度、线路动态优化阶段。提出了利用LNS-遗传算法的车辆路径规划方法，为优化路径设计了精确动态规划算法的动态优化模型，结合已有初始运行路径，及时响应实时请求，真正实现需求响应这一重要特色。

针对公交车辆调度及路径优化，提出了通过分析历史出行规律提取高概率需求点来降低需求离散度的方法。选取某区动态巴士运营区域9月份11 909条真实数据，根据实际运营情况，提炼了某时刻232条有效数据。通过编程数值试验发现，该遗传算法对于路径的求解结果偏差较小，稳定性较好。提取高概率点后，运营成本及乘客体验度均得到了明显优化。二阶段调度优化模型能够最大化地利用好车辆资源，进一步节约运营成本，具有可行性和较高的使用价值，为车辆调度及路径优化提供了应用指导。

由于系统采用的运营数据较少，客流请求量少，因此产生的孤立请求较多。该模型侧重考虑乘客体验，系统的满载率及响应率都不够高。对于今后如何选取运行区域可以使两者达到最优将继续深入研究。