低碳排放约束下城市多方式交通网络道路收费研究

张 鑫，李佳杰，俞 灏，刘 攀

(1.北京市交通委员会政务服务中心(北京市船舶检验所)，北京 100161；2.北京交通大学 交通运输学院，北京 100044；3.东南大学 交通学院，江苏 南京 210096)

0 引言

《国家综合立体交通网规划纲要》提出：“加快推进绿色低碳发展，交通领域二氧化碳排放尽早达峰”。据统计，交通运输领域碳排放年均增速保持5%以上，约占全国终端碳排放总量的15%，其中城市交通占比约为37%。因此，优化城市出行结构、提升城市交通出行效率是交通低碳发展的主要路径[1]。道路收费作为一种需求管理措施，将环境影响和交通拥堵等负外部成本内部化，促使出行者向公共交通转移，从而提高公共交通分担率、优化路网运行效率、推进交通节能降碳发展[2]。

为确定合理有效的道路收费策略，国内外学者提出了一系列道路收费模型。模型大多考虑了收费措施实施后出行者的交通方式及路径选择行为，从而更真实地评价收费策略的效益。同时，鉴于环境保护的需要，学者们建立了考虑环境因素的道路收费模型，以引导交通可持续发展。早期的研究集中在CO等有害气体控制方面。例如，Nagurney[3]建立了基于固定CO排放因子的单一模式尾气排污许可证收费的最优定价模型。Yin等[4]建立了以系统出行时间和路网污染物最小化为目标的道路收费模型，得到系统最优和排放最优不能同时达到的结论。随着交通低碳发展成为关注热点，学者们陆续考虑CO2温室气体减排约束。Li等[5]以降低碳排放与系统延误为目标，研究了随机需求下的单一模式交通网络道路收费方案。Yang等[6]研究了排放总量约束条件下单一交通网络的道路收费问题。Sharma等[7]建立了考虑CO2减排约束的多目标排放收费模型，采用多目标遗传算法求解Pareto解集，然而模型仅考虑了单一的私家车交通网络，未考虑常规公交等其他交通方式。在此基础上，部分学者构建了多方式交通网络下的道路收费模型，主要包括：私家车和常规公交[8]、私家车和地铁[9]、私家车和常规公交及地铁[10]。通过多方式交通网络的构建，可以考虑出行者在交通方式间的实际选择行为，提高道路收费方案的应用效果。

上述研究主要针对单一含碳排放物进行控制，且对综合考虑多目标优化的多方式交通网络道路收费研究较少。因此，本研究以城市交通网络中运输量最大且具有典型特点的私家车、常规公交和地铁为研究对象，结合不同含碳排放物的特点，以CO2预期减排量和CO环境容量为约束，建立综合考虑CO2排放总量和出行总时间的双目标道路收费模型。

1 含碳排放物约束

1.1 CO2减排量约束

多方式交通网络中地铁以电力驱动，将其碳排放视为0，暂不考虑电力消耗所产生的碳排放量。私家车和常规公交则假设均为传统燃油车辆(暂不考虑新能源车辆)。根据不同的适用范围和应用需求，机动车尾气模型可分为宏观、中观和微观3个层次。基于平均速度的宏观模型适用于计算区域路网的排放总量；基于典型工况的中观模型侧重于分路段、分时段的排放量计算；而基于瞬时工况的微观模型则常用于计算单车的逐秒排放量[11]。由于本研究考虑宏观交通流分布及路网整体排放量，因此，采用基于平均速度的宏观尾气模型计算路网CO2排放总量。无收费情况下初始状态的路网CO2排放总量Fbase为各交通方式出行量与单位里程排放量及行驶里程的乘积(式(1))。实施道路收费后，路网CO2预期排放总量需达到减排目标，即将初始状态排放量与预期减排量的差值作为上限值(式(2))。

(1)

la/ω2≤Fbase(1-α)，

(2)

1.2 CO环境容量

(3)

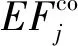
(4)

(5)

2 双目标道路收费模型

以私家车、常规公交和地铁组成的多方式交通网络为研究对象，建立了双目标道路收费模型。上层为决策者制定道路收费方案，下层为出行者根据收费方案做出交通方式及路径选择。上、下层迭代变量为路段收费费率ea，其取值范围在0和1之间，用以表示出行时间增加比例，ta为路段a上私家车行驶时间，eata为路段a的道路收费。上层模型中各交通方式的路段出行量及出行需求为道路收费费率ea的隐函数，隐函数关系可由下层交通方式与交通分配组合模型求得。

上层模型考虑效率指标(以用户出行总时间TST表示)和环境指标(以CO2排放总量TSE表示)，从而实现出行效率与环境保护的平衡。TST为私家车、常规公交和地铁的出行时间总和(式(6))。TSE为私家车和常规公交产生的CO2排放量总和(地铁的碳排放视为0)，见式(7)。寻找满足约束条件式(8)的各路段最佳收费费率ea使双目标达到约束条件下的最优值。

(6)

(7)

s.t.式(2)，式(4)～式(5),

(8)

下层模型为私家车、常规公交和地铁的交通方式与交通分配组合模型。假设地铁网络与地面交通网络完全分离，3种交通方式的划分比例服从logit模型(式(9))，私家车和常规公交的路径选择行为满足用户均衡条件(式(10)～(11))。地面交通网络中考虑公交车和私家车相互不对称影响，且出行量对其自身阻抗的影响大于另一种交通方式[14]。混合网络交通方式和交通分配组合模型的变分不等式表达形式见式(12)，该变分不等式问题等价于多方式交通配流的平衡条件[8]。私家车和公交车的出行需求平衡约束分别见式(13)和式(14)，路径出行量的非负约束见式(15)，各交通方式的出行需求总量约束见式(16)。

(9)

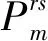
∀r,s,k，

(10)

∀r,s,l，

(11)

(12)

(13)

(14)

(15)

(16)

3 算法设计

基于Sterberg博弈的双目标道路收费模型属于N-P hard问题，上层目标函数与CO2排放总量约束条件均为非线性形式，因此无法采用传统的利用目标函数梯度信息的求解算法。遗传算法具有较强的全局搜索能力、不依赖于目标函数的梯度信息等优点，适于求解复杂实际问题。为加快收敛速度，保持种群多样性，避免早熟收敛，将“精英与协同思想”引入传统的遗传算法中，设计改进型非支配排序遗传算法(NSGA-Ⅱ)[15]求解双目标道路收费模型。在约束处理方面，采用距离测度加约束惩罚项的适应度函数构造方法[16]。本研究中距离测度为加入约束违反程度的标准化目标函数，约束惩罚项为考虑可行解比例的约束惩罚值。在流量均衡分配中考虑私家车和公交车之间的相互影响，下层模型采用精简对角化算法[17]。该算法对每次迭代的用户均衡子问题进行“全有全无”分配，分配结果作为下一个用户均衡子问题的初始解，从而加快了算法的收敛速度。模型的迭代求解算法如图1所示。

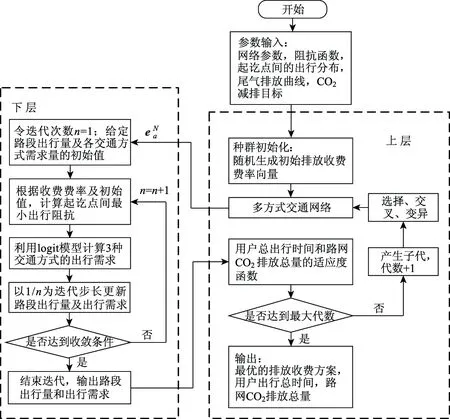
图1 模型的迭代求解算法Fig.1 Iterative solution methodology for proposed model

具体求解步骤如下。

Fi=di(x)+pi(x)，

(17)

(18)

pi(x)=(1-rf)Xi(x)+rfYi(x),

(19)

(20)

(21)

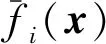
步骤4：遗传操作产生子代并进行种群更新。引入“精英与协同思想”，从非劣级别为1的层级中选择相异的2个精英个体，分别作为子种群A和子种群B的进化核心，进而进行选择子种群、交叉变异、更新种群等操作。为避免第1层级个体数量增长过快引起早熟现象，在更新种群时对全部保留非劣级别较优层级个体的方法进行改进，按式(22)确定层级j所需保留的个体数nj:

(22)

式中,nj为层级j所需保留的个体数；r为比例因子，r∈(0,1)，r值越大，第1层级选择的个体越多；L为层级总数。

步骤5：终止条件判断。若迭代代数达到最大迭代代数G，则算法结束，输出pop个最优个体以及子代与其父代的合并种群。否则转至步骤3。

4 算例分析

算例路网包括9个路段、2条公交线路和1条地铁线路，有1个OD对(1,6)，算例网络图如图2所示。路段参数见表1。模型及算法参数取值见表2。考虑交通方式间的相互影响，含有公交线路的路段的私家车和公交车的阻抗函数[19]见式(23)和式(25)，其余路段的私家车阻抗函数采用BPR函数，如式(24)所示。

表1 路段属性Tab.1 Link properties

表2 模型及算法参数取值Tab.2 Parameter values for model and algorithm

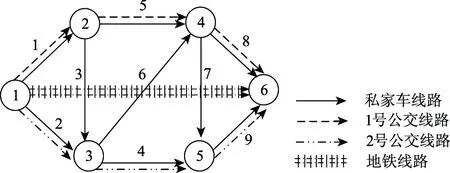
图2 算例网络图Fig.2 Test network

私家车的路阻函数为：

(23)

(24)

公交车的路阻函数为：

(25)

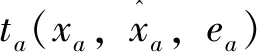
采用NSGA-Ⅱ求解双目标道路收费模型，经迭代输出全部可行解，如图3所示。位于最前端的Pareto前沿即为模型的最优解集，如图4所示。

图3 Pareto可行解解集Fig.3 Feasible Pareto solutions

图4 Pareto最优解集(Pareto前沿)Fig.4 Optimal Pareto solutions(Pareto front)

为对比方案指标差异，选取Pareto前沿中3个典型结果，优化结果1和优化结果3分别为最左侧解和最右侧解，分别代表出行总时间和CO2排放量最低的方案。优化结果2为折中方案，其2项目标值均取得中间水平。将上述3个典型结果与初始状态进行对比分析，收费费率和路段(线路)出行量见3表，道路收费前后的路网指标对比见表4。

由图3和图4可知，相比于单目标模型的唯一最优解，双目标道路收费模型求解结果为不损失任一目标的Pareto解集。Pareto前沿验证了路网CO2排放量(环境指标)和用户出行总时间(效率指标)的负相关关系，二者不能同时达到最小值，因此，为使道路收费措施达到最优管理效果，需综合考虑并合理兼顾环境指标和效率指标。由于存在30%的CO2减排目标约束，图4中Pareto前沿中的所有解的CO2排放量均小于3 736 kg的排放量限值。

由表3和表4可知，在未采取收费措施的初始状态下，路段1、路段3、路段6、路段9均呈现拥堵状态(出行量大于通行能力)且超过路段CO环境容量约束，用户出行总时间为1 633.47 h，CO2排放总量为5 336.43 kg。采取道路收费措施后，优化结果1～3促使大量私家车出行者向公共交通转移(常规公交和地铁)，公共交通出行量至少提升了43%，有效地缓解了路段拥堵和CO造成的环境污染，同时CO2排放总量下降幅度超过了32%。较初始状态，优化结果1～3的用户出行总时间呈现先下降后上升的现象。这种现象的原因在于随着道路收费费率的增加，私家车出行者将向公共交通转移，初始阶段常规公交和地铁运输能力存在一定富余，可以及时运送转移客流，同时由于私家车数量的减少，路段平均车速得到了较大提高，使得出行总时间得到一定程度的下降。然而，随着转移客流的进一步增加，公共交通能力不足，将产生较大的出行阻抗，导致出行总时间的增加。

表3 收费费率和路段(线路)出行量Tab.3 Road pricing rate and link (route) volume

表4 道路收费前后的路网指标对比Tab.4 Comparision of network indicators before/after road pricing

最后，为保证不增加初始的用户出行总时间且满足碳减排30%的预期目标，决策者可结合后验决策准则确定道路收费候选方案。算例中，在不损失初始的用户出行总时间且满足减排约束情况下，路网CO2减排比例为32%～59%，对应的用户出行总时间降低比例为2.53%～0.07%，候选方案共包括33个Pareto最优解，如图4。决策者可结合实际情况从标记区域内选择收费方案作为交通需求管控措施。

需要指出的是，针对本算例有限的道路资源环境，欲达到高于60%的CO2预期减排目标且不增加用户出行总时间，需提高公共交通的供给水平，采取公交优先措施，从而减少由私家车转移到公交出行的那部分出行者的时间损失，提高系统的运输效率。

5 结论

为了能够有效控制和降低城市交通碳排放，构建了低碳排放约束下的城市多方式交通网络道路收费模型。针对约束处理方法，采用了距离测度加约束惩罚项的适应度函数，设计了嵌套精简对角化算法的改进型非支配排序遗传算法(NSGA-Ⅱ)，对双目标道路收费模型进行求解，并通过算例分析验证了算法的有效性。算例结果表明，道路收费措施可促使私家车出行者向常规公交和地铁转移，从而降低出行总时间和CO2排放量。值得注意的是，道路收费措施的优化效果受到公共交通供给水平的影响，在算例的公共交通供给水平下，当碳减排比例超过60%时将增加出行总时间。因此，欲进一步降低出行总时间和CO2排放量，需提高公共交通的供给水平。最后，通过NSGA-Ⅱ可计算双目标道路收费模型的最优Pareto前沿，从而有效权衡效率指标(用户出行总时间)和环境指标(CO2排放总量)，辅助决策者制订合理的道路收费方案，并为优化城市交通出行结构和分析道路收费措施实施效果等提供依据。随着电子收费技术的发展，道路收费方法与电子收费技术的相互衔接尚需进一步研究。在私家车、常规公交和地铁组成的多方式交通网络的基础上，未来可进一步考虑加入自行车和新能源车辆等其他交通方式。