SHTB的拉伸冲击波谱加载方法研究
2022-06-17郭伟国赵思晗
王 凡, 郭伟国, 吴 倩, 赵思晗
(西北工业大学 航空学院, 西安 710072)
在结构受爆炸和冲击过程中,例如在轴承[1]、动能弹侵彻、油气钻探、工程冲击钻等过程,结构材料的应变率和温度往往是变化的,。为了揭示加载历程和应变率历程对材料变形的影响,研究者进行了材料的多次加载和应变率跳跃试验研究。周惠久等[2]发现在多次冲击下,强度高塑性低的材料具有更好的抗冲击能力。Cao等[3]研究碳化硅颗粒增强铝基复合材料的压缩性能时发现,多次冲击产生的破碎颗粒会提高材料的塑性应力。Nemat-Nasser等[4-5]通过多次加载、卸载过程对试样进行等温试验。为了研究动态加载下包辛格效应对于材料性能的影响,Thakur等[6]参考Nemat-Nasser的单次加载分离式Hopkinson压杆(split Hopkinson pressure bar,SHPB)[7],同时使用单次加载分离式Hopkinson拉杆(split Hopkinson tension bar,SHTB),通过多次试验的方式对试样进行压缩和拉伸,实现了应变率的改变,并在研究中发现沉淀强化的230合金的包辛格效应随应变率的增加而增大,未经强化的230合金在静态下不表现出包辛格效应。
同时研究者为研究复杂加载历程下材料的动态响应,不断开发和改进可进行多次连续冲击以及变加载率的加载设备。Lindholm[8]最早利用了SHPB装置中反射波在入射杆撞击端反射产生的第二次加载波,研究了加载历史对材料力学性能的影响。在压缩试验中,通过控制撞击杆的几何形式,容易实现历程复杂的压缩加载波,例如李夕兵等[9-11]通过改变不同结构形式的子弹冲头,改变了加载幅值历程,实现三角波、半正弦波、阶梯波等不同形式的复杂加载。Luo等[12]为了研究破甲过程中陶瓷装甲在承受初次冲击破碎后的后续冲击响应,使用撞击杆-弹簧-撞击杆同时发射的形式,当第一根撞击杆撞击入射杆并产生压缩波后,第二根撞击杆继续向前运动压缩弹簧,并最终撞击到第一根撞击杆,再次产生压缩波,通过弹簧来控制两次脉冲的间隔。Xia等[13]设计了夹心子弹的结构,即在外弹内部放置内弹,外弹与内弹存在一定的间隙,通过控制内、外弹的间距和速度来控制两个压缩加载波之间的时间间隔,将两次加载波的时间间隔的误差控制在3 μs内。Huang等[14]基于电磁发射装置,两根撞击杆相距一定距离,并使用双电磁线圈分别对两根撞击杆进行加速,撞击速度达12.6 m/s,实现低应变率下的双脉冲加载。
对于材料的动态损伤、失效和破坏研究, SHTB装置具有独特的优势,非常适合研究各种材料,特别是含孔或缺陷材料的拉伸变形、拉伸损伤与破坏机制,并建立材料的失效判据。相比于诸多的SHPB多次连续冲击压缩试验研究,开展SHTB复杂加载历程的动态拉伸试验存在必要性和特殊的意义。
直接拉伸式SHTB装置[15-16]于20世纪60年代被研发并成功应用于材料动态拉伸性能的研究。直接拉伸式SHTB装置通过撞击管对入射杆端的凸缘法兰进行撞击,在入射杆中形成拉伸加载波。在已有的连续冲击加载装置中,Luo等使用弹簧控制入射脉冲时间间隔的方法操作复杂,且误差不易控制;Xia等的“夹心弹”式撞击管对加工精度的要求很高。因此,实现复杂连续加载的动态拉伸试验具有很大的挑战。在本文中,为了实现对材料进行复杂连续拉伸加载(即冲击波谱加载),对传统直接拉伸式SHTB装置原理进行分析,并对产生拉伸波的凸缘法兰进行改进,从而在拉伸加载杆中产生所需要的连续变幅加载脉冲,进而研究材料在连续冲击波谱加载下的力学行为。
1 冲击波谱的产生原理
1.1 SHTB中拉伸加载波产生原理
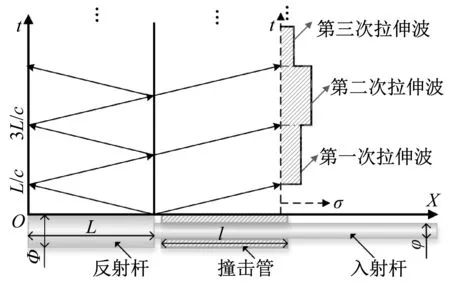
直接拉伸式SHTB中拉伸加载波产生原理如图1(d)所示,长度为l的撞击管沿拉伸加载杆加速,并撞击直径为(和长度为L的反射杆。首先在拉伸加载杆中产生第一次拉伸波,并在反射杆中产生左行压缩波;左行压缩波传播至反射杆左端面,并反射成右行拉伸波;右行拉伸波在反射杆右端面发生反射、透射,其中透射到拉伸加载杆中的为第2次拉伸波,反射作用会使反射杆中产生第二次左行压缩波;以此类推,最终在拉伸加载杆中产生多次幅值不同的拉伸加载波。

(a) L< (b) L (c) L=l (d) L>l图1 撞击管和反射杆长度变化导致的4种拉伸加载波Fig.1 Four types of tensile loading waves caused by impact tube and reflection bar length variations 一维直杆中的反射和透射并不会改变应力波的脉宽,即反射杆中和拉伸加载杆中存在的单次压缩波和拉伸波的脉宽均相同。在撞击管中,撞击产生了右行压缩波,并在右端面自由反射为拉伸波,该反射拉伸波与撞击管中的压缩波相互抵消,起卸载作用。发生卸载作用后,撞击管中的应力处处为0。与此同时,产生了反射杆中的压缩波和拉伸加载杆中产生第一次拉伸波。当加载杆、反射杆和撞击管具有相同的波速c时,应力波的脉宽为2l/c。反射杆中的左行压缩波在反射杆中往返一次后,在加载杆中产生第二次拉伸加载波,因此产生两次加载波的时间间隔为2L/c。 根据l和L的相互关系,最终在加载杆中产生4种不同的加载波,如图1。 ① 在传统SHTB中,L特别小(L< ②L ③L=l时,相邻两次拉伸波的时间间隔恰好等于拉伸波的脉宽,各个拉伸加载波紧密相连,最终表现为长平台阶梯拉伸波; ④L>l时,相邻两次拉伸波的时间间隔大于拉伸波的脉宽,这使得两次拉伸波之间存在时间间隔(2(L-l)/c)。 为简化分析,假设带反射杆的加载杆和撞击管均处于一维应力、变形和运动状态,即任意截面的质点速度和变形处处相等。另外,加载杆的撞击截面左右的质点具有连续性,左行压缩波的质点速度v1和右行拉伸波中的质点速度v2大小相等。由于加载杆并未受到撞击管的直接作用,而是通过反射杆端面获得质点速度,因此可以认为是反射杆给加载杆施加了一个合力,定义为F2。 当初始速度为v的撞击管撞击尾端带有反射杆的加载杆后,会在加载杆中产生质点速度,撞击界面处的力和速度关系如图2。 图2 撞击时撞击界面的受力分析Fig.2 Force analysis of impact interface during impact 根据一维应力波传播理论[17-18],以及反射杆撞击截面力和位移连续的条件,有 (1) (2) 对于撞击管来说,有 (3) 在撞击管中,撞击产生的压缩波从左向右传播,并在右端面自由反射为拉伸波,该反射拉伸波与撞击管中的压缩波相互抵消,起卸载作用。发生卸载作用后,撞击管中的应力处处为0,且此时其运动速度v′有 v′=v-2v3<0 (4) 这意味着撞击管将向与初始速度相反的方向运动,并与反射杆分离,之后无需考虑撞击管的运动状态。 反射杆中经由左端面反射生成的拉伸波,在传播至反射杆右端面时会产生反射和透射。根据弹性波在一维变截面杆中的反射和透射特性,有: (5) 式中,F和T分别为反射杆与加载杆变截面处的反射系数和透射系数。记反射杆撞击界面处第i次左行压缩波幅值为σ1,i,i≥1,加载杆中第i次右行拉伸波幅值为σ2,i。定义应力幅值小于0的应力波为压缩波,应力幅值大于0的应力波为拉伸波。左行压缩波在反射杆左端面反射成右行拉伸波,在通过反射杆右端面后有 σ1,i+1=-Fσ1,i (6) σ2,i+1=-Tσ1,i (7) 联合式(5)、(6)、(7)可知: σ1,i+1=(-F)iσ1,1 (8) σ2,i+1=-T·(-F)i-1·σ1,1 (9) 因此可以得到拉伸杆中多次拉伸波之间的幅值关系 (10) 左行压缩波传播至反射杆的左端自由端面,反射成右行拉伸波,并传播至反射杆右端面的过程所需要的时间为2L/c,可以得到每次拉伸波的幅值与时间的关系,有 (11) 将无数次幅值为σ2,i的右行拉伸波在时域内进行叠加,可得到传入到拉伸入射杆中的拉伸波σ2(t)为 (12) 对于反射杆中的应力波,经过无数次反射透射,将全部传入加载杆中。当无限长时间后,根据初末状态整个系统的动量守恒,有: 2l·A2·ρ (13) 式(13)中,vi=σ2,i/(ρc)为加载杆中第i次拉伸波对应的质点速度。联合式(3)、(5)、(13),以及A1=A2+A3,可得 (14) 定义σ0为加载杆中的所有拉伸脉冲幅值之和,则: (15) 为了分析各个拉伸加载波之间的幅值关系,定义[σ2,i]为第i次拉伸波占总拉伸波的比例,其与材料属性ρc和撞击速度v无关,只与反射杆和加载杆的面积比n有关,即 (16) 由式(10)、(15)、(16)可得 (17) 为了满足拉伸加载次数要求或控制试样的的应变,在Hopkinson杆试验中,需要对多余的拉伸加载波进行消除。参考Thakur等进行单次加载和恢复试验的方式,在反射杆左端面一定距离处设置能量吸收杆,将反射杆中的多余的左行压缩波吸收,便不会在拉伸加载杆中产生后续多余的拉伸波。 当反射杆左端面恰好将第i次左行压缩波完全反射为拉伸波时,记此时反射杆左端面的位移为xi,此时拉伸加载杆上获得了i+1个拉伸加载波,可以借此控制拉伸加载的次数。为分析反射杆左端面的运动规律,定义相对端面位移[xi],其意义为xi占总端面位移的比例,且与材料属性ρ、c、撞击速度v无关,只与反射杆和加载杆的面积比n有关。结合式(2)、(8),可得其中端面位移xi和[xi]分别为 (18) (19) 以7种不同的n为例,几何尺寸如表1所示,比较不同反射杆和入射杆的截面积关系下,拉伸加载波的幅值规律和端面位移规律。根据表1和式(17)可以得到拉伸加载杆上采集到的各个拉伸加载波的相对幅值,结果如图3;根据表1和式(19),如图4所示,得到了反射杆左端面的位移规律。 表1 计算中采用的7个不同的模型尺寸Tab.1 Seven different model sizes used in the calculation 图3 不同截面积下拉伸加载波的幅值变化规律Fig.3 Amplitude law of tensile loading wave under different cross-sectional area sizes 图4 不同截面积下反射杆端面的位移规律Fig.4 End face displacement under different sectional area sizes 对于带有反射杆形式的SHTB来说,选择不同的反射杆截面积,可以控制每次拉伸波之间的幅值关系,从而满足试样的应变率要求。不考虑材料应变率硬化和应变硬化对强度的影响,在每一个拉伸波内,应变率满足 (20) 式中:c1,c2分别为入射杆和透射杆的波速;εi,εr,εt分别为入射应变、反射应变、透射应变;l0为试样的初始长度;E1、E2分别为入射杆和透射杆的弹性模量。 在满足试样应力平衡的条件下,透射波的应变幅值可以表征材料的应力,即: (21) (22) 记k为第1次和第2次拉伸波加载时试样的应变率的比值,即: (23) 联立式(20)~(23),可估计在动态试验时的需满足的入射杆应变εi(1)和试样标距段的初始截面积A0 (24) (25) 式中,入射杆中第一个拉伸波的应变幅值εi(1)可通过撞击管的发射速度来控制。通过控制入射杆、透射杆的材料,反射杆和加载杆的面积比n,调整发射速度,使用不同截面积的试样等方式可控制前两次加载时试样的应变率。 选择一种反射杆尺寸进行试验验证,反射杆和入射杆均采用18 Ni马氏体时效钢材料,透射杆采用钛合金杆。入射杆和透射杆的直径均为19 mm,撞击管与入射杆的截面积相同,两者之间有0.1 mm间隙。多个拉伸波必然会导致入射波有特别大的脉宽,入射波与反射波会产生叠加,可使用式,利用入射波和透射波计算应力-应变以及应变率曲线。另一方面,为尽量采集更多有效的入射波和透射波,应变片也应当尽可能靠近撞击端。 图5 改进后SHTB装置中的反射杆尺寸图Fig.5 Dimension diagram of reflection bar in the improved SHTB device 试验中采用的撞击管长度为250 mm,反射杆长度也为250 mm,当反射杆与撞击管长度相同时,理论上每个拉伸波应当恰好连续,没有时间间隔。使用不同气压发射撞击管,对反射杆进行撞击。应变片沿轴向,对称地贴在入射杆上,采用半桥进行测量,应变片距离试样端1 500 mm。将入射杆上的应变片采集的应变信号换算成入射杆中的加载拉伸波幅值,如图6所示。 图6 不同发射速度下的拉伸应力波谱Fig.6 Tensile waves spectrum at different emission velocities 由于每次拉伸波之间的幅值成指数衰减,主要考虑前三个拉伸波的幅值。从幅值来看,其与理论推导的结果相同,即在n=2时,每次拉伸波的幅值之比满足(σ1:σ2:σ3:…=0.33:0.44:0.15:…)。 通常情况下,普通塑性金属和超塑性金属材料都表现出比较大的应变率敏感性。钢材的流动应力对于应变率较为敏感,使用多次拉伸加载方法对钢进行变应变率试验,其中钢的试验原始波形如图7所示,采用薄铜片进行整形消除入射脉冲中的抖动。 图7 变应变率试验中杆上测得的应力波形Fig.7 The original waveform measured in the variable strain rate experiment 试样在前两次加载过程中的平均应变率,如图9虚线所示。试验中使用了应变率敏感材料,应变率的变化最终导致其流动应力增加。该材料应变ε在2%~7%的范围内的平均应变率约为850 s-1,其流动应力为500 MPa;应变ε在10%~17%的范围的平均应变率约为1 200 s-1,此时的流动应力为600 MPa。从图8中,可以明显观察出应变率硬化效应。 图8 钢的真实应力-真实应变和应变率曲线Fig.8 True stress,true strain and strain rate curves of steel 在连续两次拉伸波加载过程中,加载波幅值的变化导致材料的应变率发生变化,实现了应变率跳跃试验。最重要的是,加载过程中应变率跳跃过程的所需时间约为10 μs,见图9中和图10中的1点和2点,可认为材料在塑性流动过程中,应变率瞬间产生变化。在10 μs间隔期材料塑性变形时温度(即1、2点的温度)可认为保持不变,相当于这两点处于高应变率等温温度。但图8中绝热曲线流动应力跳跃的应力差约为100 MPa,说明流动应力差值是应变率变化的影响,也解耦了温度对材料性能的影响[19-20]。该试验与传统的应变率跳跃试验通过卸载-再加载过程完全不一样,避免了加载-卸载-再加载过程对材料性能测试的影响,提高了试验便捷性和准确性。 将此试验获得的应力应变曲线与恒定应变率的850 s-1和1 200 s-1的应力应变曲线进行比较,图9中的试样1和试样2,试样3为变应变率的应力-应变曲线,其中850 s-1和1 200 s-1应变率曲线均为各自应变率下的绝热塑性流动曲线,是通过传统SHTB设备获得的,即通过撞击管撞击凸缘薄法兰(5 mm长度)产生的拉伸波,即图1中取L=5 mm。 图9 变应变率试验和恒定应变率试验比较Fig.9 Comparison of variable strain rate experiment and constant strain rate experiments 在第一个拉伸波加载时间内,试样处于应变的初始阶段,受到的加载波与850 s-1应变率的动态试验的加载波相同,试样的应力应变曲线表现出比较好的重合性,两种试验方法得到的流动应力均为500 MPa左右。第二个拉伸加载时试样的应变率为1 200 s-1,且流动应力也与传统动态SHTB法中应变率为1 200 s-1几乎相同。证明了多次拉伸加载的结果与各自独立应变率的绝热曲线重合性较好,一次应变率跳跃试验就可获得更大的塑性变形时间以及更大的应变,也有效的检验了试样的应变率历史效应。 本文基于SHTB装置,通过使用一定长度L的反射杆代替传统SHTB中的凸缘法兰,在拉伸加载杆中产生多次幅值不同、间隔严格可控的拉伸加载波,在分析过程中,得到以下结论: (1) 当拉伸加载杆尾端的反射杆的长度较大时,撞击管加速后撞击该反射杆可在拉伸加载杆中产生多次幅值不等的拉伸加载波,且加载波之间的时间间隔的控制精度高。 (2) 通过控制加载杆与反射杆之间的面积比可控制每次拉伸加载波之间的幅值关系;通过改变撞击管发射速度,设计试样的几何尺寸和使用不同材料的透射杆等方式,可较为精准地控制前两次拉伸加载时试样的应变率。 (3) 通过一次试验就可获得两个应变率下的流动应力,且在满足应变率要求的前提下,多次拉伸加载还可满足更大应变范围的动态试验要求,即加载时间延长,试样变形应变增加。 (4) 应变率阶跃变化所需时间仅为10 μs,在如此短的时间内,可认为试样处于高应变率等温状态,只产生了应变率的变化,最终将材料动态性能的温度和应变率效应进行了解耦。

1.2 拉伸加载波的幅值和反射杆端面运动分析


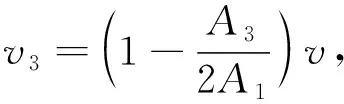






2 多次拉伸加载试样应变率控制

3 试验验证和材料验证





4 结 论
