山竹台风的非平稳风特性研究

2022-06-17谢壮宁刘慕广

振动与冲击 2022年11期

段静，张丽，谢壮宁，刘慕广

(1.华南理工大学亚热带建筑科学国家重点实验室,广州 510641；2.深圳市国家气候观象台，广东深圳 518040)

台风登陆过程城市地区高空风场特性是超高层建筑抗风设计最为关注的重要基础性问题，现场实测是获取台风特性的最可靠方法[1-2]。常见的近地风场观测主要依托地表附近的气象观测站、近年因风能资源研究所设置的高度百米以内的气象观测塔、风廓线仪等。在结构抗风研究中，为了获取高空台风湍流的特征，沿海城市的超高层建筑物顶部安装的风速仪则成为获取台风实测数据的主要来源[3-5]。出于安全方面的考虑，这些风速仪大多会安装在略高于屋面处，较难消除建筑本身的干扰影响，从而难以真正获取高空自由风场的风速数据。因而具备一定高度的气象塔获取的实测资料对高空台风描述则弥足珍贵。

良态风场的实测风速序列按照平稳随机过程处理是共识，而台风风场的实测风速序列则具有明显的非平稳特征。对于非平稳随机过程的描述主要有两类方法：①Gramer分解理论指出任意一个时间序列分解为时变确定性趋势成分和平稳零均值随机成分，把非平稳风速视为时变平均风速和平稳脉动风速的叠加[6]；②Priestly[7]提出的演变谱方法将非平稳过程表达成某个平稳过程与一确定性的调制函数的Fourier-Stieltjes积分，把非平稳风速视为时变平均风速和非平稳脉动风速的叠加。

台风风场的非平稳性分析中时变平均风速的提取是关键。早期的最小二乘拟合法、短时平均法等，后期因其自适应性而得到广泛应用的经验模态分解(empirical mode decomposition,EMD)和离散小波变换(discrete wavelet transform,DWT)都曾用于提取时变趋势项。例如：Xu等[8-11]最先基于EMD的方法，提取非平稳风速序列中的时变平均风速。申建红等[12]对比了EMD和DWT提取时变均风的精度，认为小波变换的方法更为准确可靠。吴本刚等[13-14]基于EMD的方法对超高层结构西塔顶部445 m高度的实测数据和利通广场303 m高度的实测数据进行非平稳分析,拓展了时变的物理量，验证了非平稳风速模型的准确性和优越性。安毅等[15]对台风作用下上海环球金融中心492 m高度处的实测风速序列采用EMD方法进行了高空风场分析。已有的这些工作针对非平稳台风风场的研究均是将脉动风速视为零均值平稳风速，按照平稳随机理论分析湍流特性；对于时变趋势项，不同文献均采用不同的提取方法，这些方法对风场特性参量分析结果的影响尚未进行全面的对比研究。

若研究非平稳脉动风速的时变湍流特性则需结合演变谱估计方法，常用谱估计方法包括短时傅里叶变换(short-time Fourier transform,STFT)，小波变换或者S变换等，其应用的难点在于调制函数和目标谱的确定。Huang等[16]通过改进时变功率谱密度的估计方法，对非平稳台风的时变功率谱，时变相干函数等进行研究，指出时变Karman谱和Krenk相干函数模型适合描述非平稳台风的频域特性。Wang等[17]依托苏通大桥桥址区风速记录探讨非平稳台风的时频特性，使用不同小波方法去估计时变功率谱，发现其结果和时变Kaimal谱相比差别较大。

本文根据2018年超强台风山竹发展期间深圳气象梯度观测塔(SZMGT，塔高356 m)所完整记录的三维风速实测序列，结合风场非平稳性研究方法，对平均风速剖面、湍流强度、阵风因子、湍流积分尺度、脉动风速谱等风特性参量进行全面细致的分析，希望能够加深对台风作用下非平稳高空湍流特性的理解，同时扩充极端气候下近地高空实测数据库，为工程结构抗风设计提供借鉴。

1 观测点、风况、分析内容及方法

1.1 观测点概况

用于现场实测的深圳气象梯度观测塔(简称梯度塔)位于铁岗水库库区如图1所示，其周边大范围覆盖着低矮丛林。该塔是目前国内唯一集边界层气象垂直探测、大气环境监测、雷电防御科学研究、气象灾害实景监视于一体的综合观测及试验平台，能实现从地面到城市冠层对台风等强天气开展直接观测，也是目前亚洲第一、世界第二高的桅杆结构铁塔。利用该塔不同高度(分别位于离地10 m，40 m，160 m，320 m高度)安装的三维超声风速仪可有效测量不同高度处的时变风速，超声风速仪采样频率为10 Hz。

1.2 风况及数据预处理

超强台风山竹(编号201822)于北京时间9月7日在西北太平洋洋面生成，9月11日8时升至超强台风级，9月15日2时以超强台风级在菲律宾吕宋岛东北部沿海登陆(登陆时中心附近最大风速为65 m/s)，9月16日17时从广东台山海晏镇登陆(登陆中心附近最大风速为45 m/s)，沿西西北方向向内陆移动，并于9月17日17时停止记录。根据深圳气象台的站点记录结果，最大瞬时风速为48.7 m/s，最大10 min平均风速为40.7 m/s。图2为深圳台风网记录的超强台风山竹的路径示意图，图中标注的是9月16日全天的气候信息。台风在移动过程中与深圳市最近距离大约120 km。

根据台风持续时间和移动路径，筛选出的数据分析样本为9月16日00：00时—9月16日24:00时，共24 h的记录数据。按照10 min基本时距划分子样本，由于存在4个梯度高度，24 h内共计144×4=576个子样本，子样本按顺序依次编号。

强风过程伴随的恶劣环境因素会影响测量数据的有效性，数据分析前需对原始数据进行预处理[18]，针对数据中的无效、个别缺失和奇点数据进行处理。在数据处理过程中发现320 m高度处14:00—17:00记录时段以内有8个子样本无效，分析时予以舍弃。

超声风速仪记录的三向瞬时实测风速序列记为ux(t),uy(t)和uz(t)。传统矢量分解法对风速风向的转换可参考吴本刚等进行。考虑台风的风速和风向的时变特性时，矢量分解可参考以下公式进行

(1)

(2)

(3)

1.3 非平稳性研究方法

分析风速的非平稳特征时需先提取风速的时变趋势，再进一步检验其非平稳特征。时变趋势通常采用DWT或EMD方法。

采用DWT提取时变趋势项时，首要考虑的是小波母函数选择，核心问题在于分解层数的确定。小波母函数应选择具有紧支集正交性的小波簇，例如db小波簇、coif小波簇、sym小波簇，本文采用精度较高的db10波；确定最佳分解层数时，先对信号进行最大分解层数分解，分别计算出各层小波能量，取小波能量突变层为最佳分解层数。本文利用最佳分解层数的低频近似项经小波逆变化得到最优趋势，作为信号的时变趋势项。

考虑到EMD分解时可能出现的边界效应和模态混叠问题，本文作了相应的处理。针对边界效应问题,采用AR模型进行端点数据延拓,前后各自延拓20个数据点；针对模态混叠问题，采用了集合经验模态分解(ensemble empirical mode decomposition,EEMD)，其中添加高斯白噪声的标准差为0.01，添加噪声的次数为50。将原始信号按照从高频到低频的方法分解成若干IMF分量，最后一项为残差项，一般将残差项和若干低频项叠加即可认为是趋势项。吴本刚等指出，残差项叠加最后1～3项低频项可大致认为是信号的时变趋势项。本文通过分析认为残差项叠加最后2项低频项即可合理描述信号的时变趋势。

提取趋势项后的数据是否满足平稳性，有很多的数学检验方法[19]，例如图检验法，轮次检验法，逆序数检验法，单位根检验法等。综合比较后，本文选择逆序数检验方法对数据进行平稳性检验，其原理是将数据划分多个子段，按顺序形成子段的均值序列和方差序列，统计逆序(前面的数据大于后面的数据)的总数，构造统计量，并进行非参数假设检验，从而判断数据的平稳性。

1.4 分析内容

对应于非平稳模型，相应要分析的主要脉动风场参量分别为湍流强度、阵风因子、湍流积分尺度和脉动风速功率谱。湍流强度定义为

(4)

式中:上标*表示非平稳模型;没有上标*表示平稳模型的湍流强度(下同)。相应三个方向的阵风因子为

(5)

式中，tg为阵风风速的平均时距，一般取为3 s。湍流积分尺度根据脉动风速的自相关函数采用下式计算

(6)

式中,τ0.05为自相关系数降至0.05对应点[20]。用于对比的纵向脉动风速功率谱采用以下公式

(7)

2 结果分析

2.1 时变均值提取对比

为比较不同方法提取时变均值后的效果，对整个分析时长的水平方向瞬时总风速，采用平稳模型方法(SMM)、DWT和EEMD分别提取其时变均值的结果如图3所示。由图3可见，三种方法提取的时变均值曲线和瞬时曲线的波动起伏趋势一致，同时基于DWT或者EEMD方法的时变曲线基本围绕SMM时变曲线上下波动。值得注意的是，图3(d)中三种方法时变均值的缺失段涵盖了缺失数据所处的子样本整体长度。

(a) 10 m

(b) 40 m

(d) 320 m图3 时变均值对比Fig.3 Comparison of time-varying mean value

对水平方向的瞬时总风速提取时变均值后的剩余分量的方差进行分析。根据DWT的提取结果进一步计算10 m、40 m、160 m和320 m高度处的剩余分量方差分别为1.82、1.77、1.75和1.73，EEMD的相应结果为2.45、2.54、2.65和2.60，SMM的相应结果为2.65、2.79、2.90和2.89。对实测数据提取时变均值后，DWT对应的剩余分量的方差结果是最小的，所以申建红等认为使用小波变换提取信号的时变趋势项精度相对更高。

2.2 纵向平均风速剖面

取涵盖最大风速时段(14:30—15:50)的台风纵向平均风速剖面分析。基于各种方法绘制了该时段内10 min时距的子样本平均风速剖面，并与现行GB50009—2012《建筑结构荷载规范》[21]建议的B类和C类地貌对应的风速剖面进行比较，结果如图4所示。图中DWT和EEMD 方法计算10min时距的平均风速时取相应时距内时变平均风速的均值。由图4可见，大风时段梯度塔的实测平均风速剖面更接近C类地貌对应的风剖面(规范中对应地面粗糙指数取值0.22)。比较运用不同方法计算的同高度处的相对风速比值，SMM计算结果最大，EEMD方法次之，DWT方法最小。

(a) SMM

(b) DWT

2.3 样本的平稳性检验结果

采用逆序检验法对基于各种方法分离的脉动风速的平稳性进行检验，结果如图5所示。逆序检验方法中子段长度会对检验结果产生影响。本文取子段长度30(对应平均时距3 s)，对10 min子样本的均值统计量进行假设检验。总体而言，采用DWT和EEMD后数据的平稳性优于SMM，说明提取时变趋势项后，数据平稳性更好。当子段长度为30时，SMM中所有高度测点数据平稳性平均通过率为75.98%，而对应于DWT和EEMD方法的平均通过率分别为97.88%和97.08%。平稳性检验的结果为将脉动风速按照平稳随机过程进行分析提供依据。

图5 数据平稳性检验Fig.5 Data stationarity test

2.4 湍流强度

湍流强度反映了风速脉动的相对强度，是对大气湍流最简单的描述。不同来流方向对应的下垫面粗糙度不同，可能会影响到该处的湍流强度。SZMGT在台风山竹期间的实测风向角记录，在文献[22]中给出了详细说明，其中风向转变明显时段正对应风速时程的大风时段。根据式(4)，取基本时距为10 min的各向子样本计算，基于不同方法讨论不同高度湍流强度随风向角的变化规律，结果如图6所示。由图6可见，湍流强度分量随高度的增加而减小；采用不同方法计算得到的湍流强度存在一定差异，SMM计算的湍流强度最大、EEMD的计算值次之、DWT的最小，这和以上采用这3种方法计算脉动风速方差的差异特征是一致的。同时在东风及其附近(远场地貌上对应的是高度900 m左右的羊台山森林公园)，不同方法计算的各向湍流强度相对最大，该变化趋势随测点高度的增加更为明显。

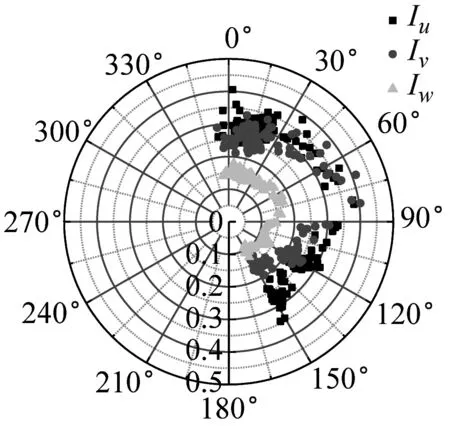
(a) 10 m-SMM

(b) 40 m-SMM

(d) 320 m-SMM

(e) 10 m-DWT

(f) 40 m-DWT

(g) 160 m-DWT

(h) 320 m-DWT

(i) 10 m-EEMD

(j) 40 m-EEMD

(k) 160 m-EEMD

(l) 320 m-EEMD图6 湍流强度随风向角变化Fig.6 Variation of turbulence intensity with wind direction

进一步分析湍流强度分量的变化规律，计算不同高度子样本三个方向湍流强度的均值之比，结果如表1所示。由表1可见，采用SMM得到的低空测点其三向湍强比值基本稳定在1∶0.84∶0.52，这与JTG/T 3360-01—2018《公路桥梁抗风设计规范》[23]中建议的Iu∶Iv∶Iw=1∶0.88∶0.50较为接近；高空测点湍强比值随高度增加而增大；其他方法也出现了湍强比值随高度增加而增大的现象。提取台风的时变趋势项后，各项湍流强度虽然较平稳模型计算结果小，但是台风横向湍流和竖向湍流相对增强，较桥梁规范建议比值偏大。

表1 三向湍强比值Tab.1 Turbulence intensity ratio

从建筑抗风设计的角度，纵向湍流强度沿高度的变化规律是工程师关注的重点。现将各种方法计算的湍流强度剖面和规范推荐的4类地貌对应的剖面进行比较，结果如图7所示。由图7可知，SMM和EEMD方法计算的纵向湍流强度剖面与D类地貌比较接近，DWT计算的纵向湍流强度剖面略小于C类地貌对应剖面。

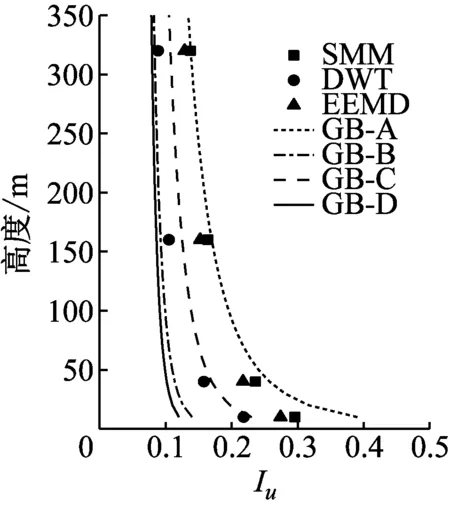
图7 纵向湍流强度剖面Fig.7 Longitudinal turbulence intensity profiles

2.5 阵风因子

阵风因子与湍流强度及阵风持续期的关系是结构风工程中关注的热点问题[24]。本节以3 s阵风持续期讨论基于不同方法和高度计算的阵风因子随湍流强度的变化规律如图8所示。然后讨论不同阵风持续期和基本时距与阵风因子的相互关系。

(a) Gu-SMM

(b) Gv-SMM

(d) Gu-DWT

(e) Gv-DWT

(f) Gw-DWT

(g) Gu-EEMD

(h) Gv-EEMD

(i) Gw-EEMD图8 阵风因子随湍流强度的变化Fig.8 Gust factors versus the turbulence intensity

由图8可见，阵风因子和湍流强度关系呈高度相关性；阵风因子随高度的增加而减小。采用不同方法计算得到的阵风因子存在一定差异，SMM计算的阵风因子最大、EEMD的计算值次之、DWT的最小。

进一步分析纵向湍流强度和阵风因子之间的关系，Gu不只是和Iu有关，还取决于风速的平均时距T和所考虑阵风的持续时间tg，通常用下式表示

(8)

式中:k1和k2为两个待定的常数，可通过拟合的方法获取。在T=600 s，tg=3 s的工况下，本文拟合得到的k1为0.55，k2为1.14，和Cao等建议k1为0.5，k2为1.15较为接近。

阵风因子的大小与阵风持续期tg和基本时距的选择有关。对10 min和1 h两种基本时距，以纵向阵风因子为例，对比不同方法计算的各高度阵风因子随持续期的变化规律，结果如图9所示。由图9可见，阵风因子随持续时距的增加而减小，在单对数坐标下呈现非线性变化；随基本时距的增加而增大；随高度的增加而减小。由于存在高度相关性，采用不同方法计算得到的阵风因子的差异特征和湍流强度的差异特征一致，以10 m高度10 min基本时距实测结果为例，基于SMM、DWT和EEMD方法计算的纵向阵风因子均值分别为1.795、1.445和1.557。该结果可认为是按照实测平均风剖面判别的C类地貌的结果，按照规范给出的良态风气候下阵风因子估算公式G=1+gIu(g取2.5)，C类地貌下阵风因子取值为1.575，与EEMD结果比较接近。

(a) 基本时距10 min(10 m)

(b) 基本时距1 h(10 m)

(d) 基本时距1 h(40 m)

(e) 基本时距10 min(160 m)

(f) 基本时距1 h(160 m)

(g) 基本时距10 min(320 m)

(h) 基本时距1 h(320 m)图9 阵风因子随时距的变化Fig.9 Gust factors versus the sample duration

2.6 湍流积分尺度

相对于以上所讨论的其他风场参数，湍流积分尺度的离散性要更大一些。以纵向湍流积分尺度为例讨论其离散性和分布规律，结果如图10所示。由图10可见，采用SMM计算得到的Lu相对离散，随平均风速的增加而增大的趋势最明显；DWT计算的Lu相对最小，随平均风速增加而增大的趋势相对不明显；EEMD方法计算的Lu介于SMM和DWT之间，随平均风速增加而增大的趋势相对明显。

(a) 10 m

(b) 40 m

(d) 320 m图10 纵向湍流积分尺度随平均风速的变化Fig.10 Variation of Longitudinal turbulence integral scales with mean wind speed

取纵向湍流积分尺度均值分析其沿高度的变化规律，并与日本规范提供的推荐值对比，结果如图11所示。由图11可见，SMM计算的湍流积分尺度剖面和AIJ—2004《AIJ recommendations for loads on building》[25]的推荐剖面较为一致；EEMD计算结果次之，约为SMM计算结果的1/2；DWT的计算结果最小，约为SMM计算结果的1/7。这个结果与Tao等[26]采用DWT对苏通大桥的实测湍流积分尺度的分析所得到湍流积分尺度偏少的结论相一致。

图11 纵向湍流积分尺度剖面Fig.11 Longitudinal turbulence integral scale profiles

相比于图7所表示的不同方法得到的湍流强度的变化和差异，不同方法所得到的湍流积分尺度分布的差异更为显著。本文认为，在采用非平稳方法提取时变平均风速时把将真实脉动分量中的低频部分一并提取掉是产生这个问题的主要原因，后续在对比湍流谱中可以得到进一步的证实。

2.7 脉动风速谱

对于脉动风速谱，以纵向脉动风速谱为例，取大风时段1 h(13:00—14:00)的实测数据进行分析，并与Von-Karman谱进行对比，结果如图12所示。其中Karman谱公式中湍流积分尺度参照AIJ—2004推荐公式进行计算。由图12可见，在不同高度处，SMM和EEMD的实测脉动风速谱比较接近且和Karman谱一致性较好，而DWT的实测脉动风速谱在低频段明显偏低，其湍流能量明显偏小。脉动风速谱的变化规律可进一步佐证DWT方法在提取时变均风时，可能将属于脉动风的某些长周期成分作为平均风一并提取，导致与频域相关的风场特性参量明显偏低、尤其是对低频分量极为敏感的湍流积分尺度。