基于损失函数的单元测试用例自动化生成算法研究与实现

傅瑞华， 李 凡， 王俊峰

(四川大学计算机学院， 成都 610065)

1 引 言

软件测试是软件质量保证的核心环节， 是软件产品生命周期内质量保证不可缺少的有效措施.证据表明，目前完整的软件测试过程最多可占项目开发总成本的40%[1]，而早期及时通过软件测试可大大降低修复软件生命周期中的缺陷的成本[2].但目前，仍有相当多的软件是依靠手工编写测试用例来进行软件测试.这种人工方式需保证测试人员有较多经验和较高技术水平，且在有高质量测试人员情况下依旧会花费较高的成本(时间、人力)，也并不能完全保证测试用例的高覆盖率和软件质量.因此研究测试用例自动化生成技术成为了软件开发行业发展的必然趋势.

测试用例的自动构建可视为一个优化问题，即如何在生成最小数量的测试用例集合的标准下，尽可能覆盖更多的目标，并保证测试数据分布的平衡性，使得测试用例高有效.市面上目前已经有较多的成熟工具如Logiscope、Load Runner、Web Stress[3]等，可用于软件测试中测试用例的自动生成，但大多数仍然无法解决如何自动生成高质量测试、如何使得测试用例全面覆盖等自动化测试痛点问题，所以要实现真正意义上的自动生成测试用例，仍需投入大量研究及技术支持.

软件测试方法可大类分为黑盒测试及白盒测试，前者注重在不清楚内部结构和细节的情况下验证功能可用性；后者基于程序源码内部逻辑知识，并通过特定的测试覆盖率标准如语句覆盖率、分支覆盖率等，来检测编码过程中存在的潜在错误[4].

根据不同的软件测试方法，自动生成测试用例的常见算法可分为随机测试方法、符号执行方法、UML模型检测法和基于元启发式算法的测试用例自动生成方法等[5].李志博等[6]提出的优化的固定候选集算法(Fixed Sized Candidate Set，FSCS)在传统的随机测试算法[7]中添加了自适应方法，通过生成多个候选测试用例数据，计算每个候选数据与已执行用例数据集中最近测试用例数据之间的距离，并选择出距离最大的候选数据作为下一个执行数据，从而使得测试用例数据尽可能均匀地在输入空间内分布.Xiao等[8]提出一种以程序阶段特征为指导的新型符号技术用于测试用例的自动生成，把程序基本块执行次序划分为不同的执行阶段，但此种符号执行法易集中在局部代码块，导致其他部分的代码无法被有效测试.Swain等[9]提出将UML行为模型转换为图形，通过测试场景和测试序列来自动生成测试用例的方法.Liu等[10]提出一种通过扫描带有嵌套循环过程的源代码来构造程序层模型，并将图层模型转换为扩展的正则表达式，进而获得测试路径的方法.但当程序复杂度上升(特指循环嵌套)时，该方法会导致测试序列爆炸问题.

元启发式测试用例自动生成算法是根据测试充分性标准自动生成最优解测试用例集，包括粒子群优化算法[11]、遗传算法、模拟退火算法[12]、蚁群算法等[13]，其中遗传算法应用最为广泛.Bao等[14]提出的改进遗传方法(Improved Adaptive Genetic Algorithm，IAGA)旨在每次迭代中根据个体相似度和适应度值的差异，动态调整一些参数来提高早熟收敛方面的搜索性能.相比于其他算法，元启发式算法可适用于更大规模及更高复杂度的空间，并能更敏捷地找到最优解或近似最优解[15].但由于算法受限于适应度函数且依赖于初始种群，容易产生以下问题：算法时间复杂度过高、种群过早收敛、非全局最优解以及局部最优导致数据冗余.

为进一步解决以上所述的元启发式算法缺陷，并使得生成的测试用例在数量较少的情况下能够覆盖尽可能多的路径，本文提出一种基于损失函数的白盒测试用例生成方法：在GA算法过程中实时判断种群数据的分布并进行动态调整，并根据分布情况自适应调整交叉变异算子，同时通过改进后的适应度及精英策略评估函数来对种群进行选择，以保证每次迭代的初始输入种群的有效性，最大程度构建出高覆盖低数量高有效的最优解测试数据集.

2 相关概念

2.1 损失函数

在机器学习模型中，单个样本的真实值与预测值的差值称作损失，损失值越小表示模型越贴合真实场景.其中用于计算损失值的函数被称作损失函数，其本质是一个用于找到场景最优解的目的函数，可被用于度量一个模型的好坏，所以损失函数是机器学习中检验模型结构风险的重要组成部分.

构建的模型能够通过损失函数计算出的损失值，反向去传播更新各参数，使得模型生成的预测值能够更好地拟合真实值，从而判断模型或者决策的好坏.当损失值小于既定的阈值后，则可停止学习得到最优模型.假设存在离散点(xi，yi)的集合，针对单一参数预测函数f(xi)=α1+α2xi，有平方误差代价函数：

(1)

其中，N为总样本数量；i表示第i个样本.求解最优值即为求解参数α1，α2，使得函数J值极小从而获取最佳预测函数与最小误差.

2.2 GA算法

遗传算法已在多学科中被用作解决全局搜索优化的方案，可形式化将该算法内容用一个多元组进行表示.

G=(C,F,O(α,β,γ),R(c,m,n),E)

(2)

表1 多元组符号含义

遗传算法在每一次迭代中，通过适应度函数选择更优的个体至下一代，再对种群进行交叉或变异操作，从而产生新的种群.

使用遗传算法实现测试用例的自动生成可描述为:在每轮迭代过程，遗传算法使用当前种群(即测试用例)来驱动被测程序的执行，并以最大化程序路径覆盖率作为适应性函数进行计算，通过交叉变异等操作优化有效性较低的测试用例数据，进而产生下一代种群至循环结束.

2.3 动态符号化执行

动态符号执行在传统符号执行方法之上，让具体值和符号执行同时进行[16].动态符号执行技术在生成测试用例时使用程序变量的具体值来替换复杂表达式或数据结构中的符号变量，通过简化路径条件自动生成更有效的测试用例，且具有较小的时间花销[17].程序生成随机数据进行第一次执行，并从当前执行路径上的分支语句的谓词中搜集所有符号约束，谓词的定义如后式：P(x1,x2,…,xi)，其中xi为独立的个体(表示不同事物或某种抽象概念)；P表示一种行为约束，刻画出个体间的关系及性质.

之后对约束进行修改生成新路径的约束序列，并利用约束求解器求解出另一个可行的新输入.通过输入迭代产生变种输入，从而触发程序新状态，发现所有可行路径下的测试用例数据.

3 算法概述

本文提出的单元测试用例自动化生成算法整体上需达成的目标为：保证测试用例数据高覆盖高有效，平均覆盖率尽可能达到α(α>=95%).在测试停止标准中基于测试用例的原则下，非功能性测试用例覆盖率达到或超过95%允许正常结束测试[18].

图1 种群个体恶性倾斜示意图

保证分布平衡，分散重复路径分支下的冗余个体，使得迭代完成后各路径之间的种群数量差值β<=5.防止收敛速度过快导致的早熟以及单路径数据爆炸(如图1)等问题缺陷.图1中Bi为分支Li为语句，虚线框中的部分代表聚集了较多的种群个体，因此在迭代中测试重点会偏向根节点B1的右子树路径上，从而导致失衡，造成最终种群迭代的恶性结果效应.

3.1 测试用例自动生成模型框架

本文提出的单元测试用例自动化生成算法(LFGA)模型如图2所示.整体方法中含有程序分析、GA优化、最优种群集合评估等主要模块，对初始测试程序进行插桩测试，并于中间过程引入损失函数验证，通过及时判断迭代各种群个体是否符合分支预期，动态根据路径前序分支覆盖情况调整种群在程序路径树的分布，执行时无需过度依赖于初始种群，最后以适当收敛速度及迭代次数来确定最优数据集，增强此种问题场景下通用模型的整体鲁棒性及种群个体耦合依赖性，并以此可推断至较为复杂软件的用例生成.

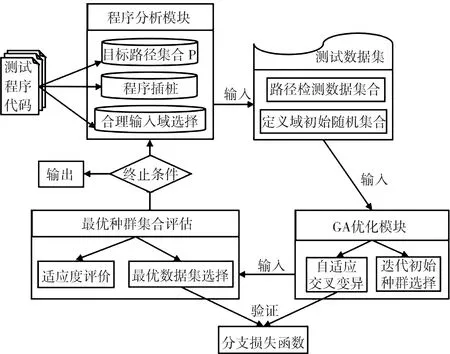
图2 基于损失函数的测试用例生成模型Fig.2 Test case generation model based on loss function

3.2 程序分析

模型中程序分析采用静态预分析方式，抽取程序片段中的关键信息包括分支节点、参数集合、输入域范围等，以Java语言为例，借助ASTParser类遍历形成DOT类型文件数据，再利用正则从节点语句中获取具体的输入域范围，具体DOT数据类型如表2所示.

表2 DOT文件数据结构字段

生成的dot文件同时包含了各个id之间的指向信息，能够表示各分支之间的层级关系，访问者根据dot文件数据中的节点语句信息可得到分支集合T={t1,t2,...,tn}.给定路径集合P={p1,p2,...,pn}，其中pi∈T，且pi代表的子集没有重复，所有子集的并集涵盖程序整个分支集合;若存在pm∈pn则仅保留最长路径子集.

将所有路径信息进行优化后，执行统一插桩，把测试数据集映射至路径检测及定义域初值数据集.路径检测数据集合在分支损失函数验证阶段将被用于控制种群在各路径上的分布，定义域初始随机集合将用于种群(测试用例)初始值的生成.

3.3 初值随机生成优化

关于种群迭代演化的测试，前期输入域有效性间接性确定了后期迭代时间长短及收敛速度的快慢.之前经过对代码片段的静态分析并确定了类的分支行为，在DOT数据集合上进行二次正则精简来获取每一个分支中可能存在的参考值以及其对应范围符号，包括：>、<、=、&、！等，然后以预设数量的种群个体数在变量参考范围内随机生成初始种群，组成由范围内随机测试用例组成的测试套件，再用于之后迭代.

由于并非所有程度控制条件中含有明确变量信息(如:无数值仅有等式约束关系)，因此考虑符号化执行思想，把输入变为符号值来得到让特定代码片段区域执行的输入组合值或关系，以图3为例，获取路径分支truefalse序列的约束关系，，根据执行树左右子树进行初值的等式约束关系集取值，从而适应于无明确参考值下的种群初值生成.改分支集合序列T中每项为ti-0和ti-1，则ti-0代表true，ti-1代表false，作为路径集合的存储信息.

图3 执行树信息存储示例Fig.3 Execution tree information store

获取到各路径下的参考值范围或变量状态关系后，将上述变量信息存储至对应分支的数据结构中，根据取值范围对各路径设置相应概率阈值，便于在分支损失函数中进行分支碰撞检测优化.

3.4 分支损失函数验证

在最优种群集合评估模块中，为确保数据集至少覆盖一次决策点的每个条件的所有可能结果(即取真、取假分支)，本文提出一种通过分支损失函数实时调整后序种群分布的验证算法，其中分支损失函数在流程中作为用于找到最优解集合的目的函数，控制选择及交叉变异方向，从而增强测试例数据之间的公平性、友好性，流程如图4所示.

在进行整体种群评估后开启分支损失函数的验证，贯穿于每代个体的选择丢弃和后续变异的突变方向等，尽可能地去掉某分支条件下的冗余测试数据，主要损失函数的实现由以下两部分构成.

图4 分支损失函数验证流程Fig.4 Branch loss function verification process

第一项：用于迭代选择过程中判断个体累计是否符合分支覆盖预期.由于前序步骤中进行了正则切割及插桩等过程，程序能够获取存储的分支数据结构信息，包括分支id、分支所含变量范围及关系、分支概率阈值等.当进入某分支的个体数占比超过设定的该分支概率阈值则选择舍弃，重新随机选取其他分支进行参考值范围内的数据随机生成以补位，再结合精英个体选择策略下的剩余种群形成新一代种群数据的有效输入;第二项：提供个体交叉变异的趋势判断.由于适应度函数的设计易使测试数据后续汇集在已生成数据的路径上(即概率阈值更大)，考虑在经过选择阶段后，通过累计各路径个体，选取数目相对较多和较少的分支种群集合进行交叉变异.算法中的变量含义对应关系如表3所示.

表3 算法变量含义对照表

整体算法思路过程伪代码如算法1所示.

算法1分支损失函数验证

1) procedure Branch Cost(，)

2) Pretreatment:T&P←dot类型数据

3) Initializa:PopList←Referencevaluerange

4) Evaluate: the primary population

5) whilei< maxGeneration do

6) Select:NewPopList←f(xi)评估

7) while in Function(CostBranch) life

circle do

8)PXover& PMutation: 自适应改变

9) if reachedPopListend

10) end while

11) 使用JUnit计算数据覆盖率

12) if test data optimal←cov(%) max

13) end while

14) 输出最优解集合

15) end procedure

3.5 自适应算子设计

采取常规遗传算法中的策略，交叉函数对选定的两个父级中的基因进行交换，变异函数实现采用的单点交叉.通常在覆盖率高的测试用例数据上修改某一个参数值或用高覆盖率测试用例中的某几位参考数据替换前一阶段新生成的测试用数据，往往能够在适当速度范围内加快收敛改善结果，有效加强进化性能[19].

当连续碰撞某分支次数累计达到设定阈值，认为在此分支参考值范围内已经设定了足够的测试用例，为避免出现过度收敛导致分支不平衡现象，动态地调整交叉变异算子.根据测试数据累计分支碰撞阈值，动态改变交叉变异算子的取值.式(3)和式(4)分别表示变异和交叉算子的调整方式.

(3)

(4)

式中，fmax代表相对适应度最大的个体；fi代表待变异个体(适应度较小的测试用例)的相对适应度；favg代表种群个体平均相对适应度.在遗传算法中Pc，Pm取值范围一般为[0.25，0.99)及[0.001，0.1)[20]，此处公式中k1及k2、k3及k4，通过随机函数分别取[0.25，0.99)及[0.001，0.1)区间内的值.

相对适应度越小的个体表示进入其对应分支的概率越大越容易进入，相对较大的变异算子在此种情况下更能促进进入冗余分支测试数据的变异.

对于分支概率最大的情况下，fi必定大于favg，使得整体Pm增加，从而对应个体变异的概率增加；对于进入分支难的个体，应使Pm变小，从而使这个个体更不容易变异顺利进入下一代.

3.6 GA优化模块

(1) 适应度函数设计.根据个体分支覆盖情况和所有种群分支覆盖情况进行个体的适应度计算，每次进行更改时需重新编译代码.越易覆盖的路径会有越多的测试数据集，适应度函数见式(5).

(5)

其中，N代表种群待选择个体总数；ui为路径集合个体pi所含有的测试数据数目；umax为测试用例在pi路径下达到理想平衡状态下的个数，越易被覆盖的路径会有更多的测试数据集，对应个体适应度值越低，在择优选择中表现为更劣势个体.

(2) 精英策略设计.结合分支验证机制之前，本文先采用轮盘赌个体选择策略，将中间步骤得到的最优解个体进行保留.结合分支损失函数验证后能在确保当代种群中最佳成员组作为二代种群的初始有效输入的条件下动态调整其余测试数据的平衡性，从而防止由遗传算法过度收敛导致的数据极端不平衡.轮盘赌策略对优劣个体的相对适应度计算式如式(6).

rf(i)=f(i)/∑f(i)，i≤N

(6)

式中， ∑f(i)表示当前适应度的总和.个体相对适应度rf(i)越高表示个体更优良，将保留至分支损失函数执行阶段.

4 实验与结果

本文实验选择了5种不同复杂度的被测程序来进行所提出方法的评估，并与其他方法和工具进行横向对比实验，算法实现采用Intellij IDEA软件环境，开源测试框架JUnit辅助进行测试结果优劣分析.实验评估标准以回答以下两个问题：Q1: 本文提出方法是否能够优化数据收敛结果，并提高总体覆盖率？Q2: 与其他方法相比，本文提出方法是否能够在相同规模的测试数据集合下，实现更高的覆盖率结果？

4.1 实验过程

实验测试采用软件测试中的经典模型Triangle， Next Date， GCD， premium， decision[21]等作为被测程序来验证所提出方法的可行性(如表4).

表4 测试模型信息

本文提出的方法记为LFGA，随机算法记为RA，蚁群算法记为ACA，标准遗传算法记为SGA，开源工具Evosuite中的改进遗传算法记为IGA.Evosuite[22]基于传统GA算法，然后迭代地使用变异和交叉等遗传算子来进化.

通过使用不同的算法对上述5种待测程序模型进行单元测试用例的自动生成，并通过Junit进行测试用例数据的覆盖率计算输出及后续结果对比.实验种群规模保持为50，最大迭代次数设上限500，自适应遗传操作中设置单点交叉概率上限0.9;变异概率上限0.1.实验中使用的评估指标是在预先确定的独立运行次数上实现的平均覆盖率.通常迭代停止机制的判断方式为两种:人为设定及数据收敛趋势稳定或陷入局部最优解.

4.2 实验结果

通过使用不同算法对同种程序测试模型进行测试，生成数据的路径覆盖率结果数据如图5所示，其中cov表示多次实验累计下的覆盖率结果均值.

表5为在每种模型经过40轮次实验后，程序输出分布结果趋势稳定情况下的平均迭代次数(去除最优及最坏结果以尽量降低偶然事件误差).注:程序输出的最优结果不代表数据一定可用，仅可通过此数据判断种群收敛情况.

表5 程序稳定解下的遗传代数

图5 不同方法下的覆盖率结果Fig.5 Coverage results under different methods

为了验证被测程序的测试数据生成在改进方法下的有效性，绘制了在本文所提出的思路下，种群数据的收敛趋势(以Triangle为例)，如图6所示，并以标准遗传算法SGA下的过程中种群数据分布趋势作为对照.图中横坐标表示种群的迭代次数，纵坐标表示为种群个数，其中每一条折线表示：一条路径分支上的种群个数在迭代过程中的变化.

以含有4条分支路径的Triangle程序为例，两幅图中从上到下的折线依次代表4条路径上种群数量的变化.经过20余次迭代后，在图7的SGA算法中，每条路径上的种群数量变化波动较大且无明显收敛趋势；而在图6的LFGA算法中，每条路径上的种群数量变化趋于平缓，且各路径之间的分布的种群数量差值也呈现越来越小的趋势.

图6 LFGA种群收敛趋势(以Triangle为例)Fig.6 Convergence trend of LFGA population (take Triangle as an example)

图7 SGA种群分布图(以Triangle为例)Fig.7 SGA population distribution trend (take Triangle as an example)

4.3 数据分析

根据实验结果，结合第4节开篇，Q1和Q2数据分析情况如下.Q1:从表5展现的数据中可看出传统方式生成数据虽然经过较少的迭代总数，但测试数据可用性远远低于本文提出的方法，说明传统算法使得种群数据过快收敛或陷入局部最优中，从而通过本文中的分支损失函数验证方式，能够较好地让种群数据分布得到有效的筛选，并通过图5生成测试数据的路径分布图可看出，整体数据以适当速度进行较稳定的收敛，最终达成最优解较均匀覆盖目标路径目标.Q2: 横向对比方式下如表4数据，本文方法生成数据对于几个测试程序来讲生成了较好的覆盖率且高于SGA算法，数据可用性更高，同时Evosuite开源工具数据覆盖率比较稳定可作为本文方法参考目标覆盖率，LFGA算法中的覆盖率与Evosuite数据覆盖率也更为接近，说明文本所提出损失函数方法适用于测试数据的自动生成.

5 结 论

本文提出了一种基于损失函数的方法，目的是通过判断算法过程中平衡性变化，改进种群适应度及精英策略评估方式，并利用分支信息优化自适应交叉变异算子，自动完成数据收敛过程，生成最小高覆盖有效测试用例集.经过大量实验及数据表明，本文方法能够有效收敛种群，增强算法全局寻优能力，并较好解决初值依赖、收敛早熟、局部寻优能力滞后等传统缺陷，尽可能地提升搜索效率及数据有效率，将测试覆盖度达到一个满意的值，对快速生成满足测试要求的数据有着重要意义.由于本文所提算法能够通过判断用例数据分布情况来自动完成数据收敛的过程，后续引入神经网络进行训练是值得尝试和研究的.