深度学习理论下单元作业设计与思考——以人教版数学九年级下册《锐角三角函数》为例

郭炜颖 赵 旭

（福州第十八中学，福建 福州 350001）

1976 年美国学者马顿和萨尔乔借鉴布鲁姆认知分类理论，在论文《学习的本质区别：结果和过程》中首先提出教育领域的“深度学习”概念。2006 年加拿大学者辛顿在《科学》杂志上刊登了深度学习的相关论文，激起了深度学习的研究热潮。同年，华中师范大学发起推动以发展能力为目标深度教学研究，主张提高学科能力，开展深度教学。2010 年国务院颁布的《国家中长期教育改革和发展纲要》提出，只有实施深度学习，才能真正增强学生的创新力和自主学习能力，至此国内开始广泛的重视深度学习的研究。［1］2021 年4 月12 日，教育部办公厅发布了《关于加强义务教育学校作业管理的通知》，通知中提到“教师要提高自主设计作业能力，精准设计作业，精选内容，系统化选编，体现素质教育导向，提高作业设计质量。”笔者认为以深度学习理论为主要设计理念，以单元为整体的单元作业设计，对挖掘教材本质，整体把握知识结构，渗透教学价值，发展学生核心素养起到了有效的作用。本文以人教版数学九年级下学期《锐角三角函数》为例，对在深度学习理论下单元作业设计的设计理念、设计思考及部分作业展示说明。

一、基于深度学习理论的单元作业设计理念

深度学习是指通过对教学核心内容的分析和教材的整合，通过学生认知参与，获得知识、过程、方法、价值的深度感悟，完善发展认知结构，形成学习能力，并能将这种能力迁移至新的情景，有效解决挑战性问题的学习，以促进知识建构、注重批判理解、强调信息整合，注重迁移应用、面向问题解决为基本特征，以发展学生高阶思维与能力为目的，这与当今培养学生核心素养的教育理念相吻合。

数学单元作业设计是指教师根据单元中的数学知识，以整合的思路来设计这个单元的作业。通过知识聚集，把本单元中零碎的知识要点串联在一起。对教学内容“结构化”进行组织，加强模块或主题间的结合，注重各单元知识之间的相互联系，从而使学生对整个单元理论体系产生全面、深刻理解，形成良好的认知结构。

数学单元作业设计理念中的整合性、联系性正是深度学习理论中的重要理念，除此之外，基于深度学习理论下的单元作业设计还应重视知识的本质由来和系统建构，注重知识的迁移性，注重知识理论工具性及实际应用性，从而使学生通过单元作业的训练，对本单元知识体系产生全面、深刻的认识，强化知识的应用能力，提高分析解决问题的能力。

《锐角三角函数》是人教版数学九年级下册教材的第二十八章的教学内容，学生已经学习了初中数学的大部分知识内容及思想方法，而这一单元与高中《三角函数》模块的学习密切相关，是初高知识衔接的一个关键点。基于深度学习理念，从完善发展认知结构角度来看，《锐角三角函数》在几何领域是初中三角形研究的最后阶段，在代数领域它又是初中学习的最后一个初等函数。从知识联系角度来看，锐角三角函数与相似三角形、勾股定理等知识密切相关，且与圆、四边形等章节均可产生联系。从迁移应用、面向问题解决角度上看锐角三角函数对几何图形定量研究提供了工具性的作用，在实际问题中有着大量应用。

基于上述论述，本文拟从知识构建、知识迁移、知识整合三个方面来探讨基于深度学习理论下该单元作业设计的策略。

二、深度学习理论下的单元作业设计策略

（一）知识构建：深度理解锐角三角函数知识内涵与外延

这一章节知识内涵有：1.锐角三角函数是以相似三角形知识为基础，刻画了直角三角形边角之间的关系。2.锐角三角函数值与角所在的直角三角形无关，只与角度的大小有关，其锐角三角函数值唯一确定，等角的三角函数值相等。反之，对于给定的锐角三角函数值可以求出对应的唯一锐角角度大小。角度的大小与锐角三角函数值之间呈一一对应关系。3.锐角三角函数是实现边与角关系互相转换的重要桥梁，可以通过锐角三角函数相关知识“知边求角”，或是“知角求边”。这一章节知识外延主要有：1.锐角三角函数是数形结合思想中“以数解形”思想的体现，将几何问题转化为代数问题，在高中后续课程学习中，将专门从函数的眼光来讨论三角函数的相关性质。2.三角函数的概念在整个数学中的应用大量存在，例如，高中解析几何中直线斜率的概念正是通过正切进行刻画。基于上述分析，笔者以相似三角形为该单元知识的生长点，以等角的三角函数值相等这一性质作为与该单元知识核心要点，以斜率概念的渗透作为该单元知识的重要外延，形成知识构建。设计了如下单元练习，目的在于让学生全面领会三角函数知识内涵，弄清三角函数概念的由来、深层含义，为后续教学的应用作铺垫。

例1 如图1、2，在Rt△ABC与Rt△DEF中，∠A=∠D，∠C=∠E=90°，求证：cosA=cosD.

图1

图2

解题思路：由∠A=∠D，∠C=∠E，可知：△ABC相似于△DFE，得到，证得：cosA=cosD.

设计意图：许多学生学完一整章对于余弦值定义的唯一确定性认识还是不到位。只要角相等，那么对应的余弦值也相等，余弦值的大小与角所在的直角三角形无关。理解余弦定义的本质由来，加深对余弦乃至锐角三角函数定义的认识。

例2 如图3，在Rt△ABC中，∠ACB=90°，D是AB的中点，CD=3，AC=4，sin∠DCB=______

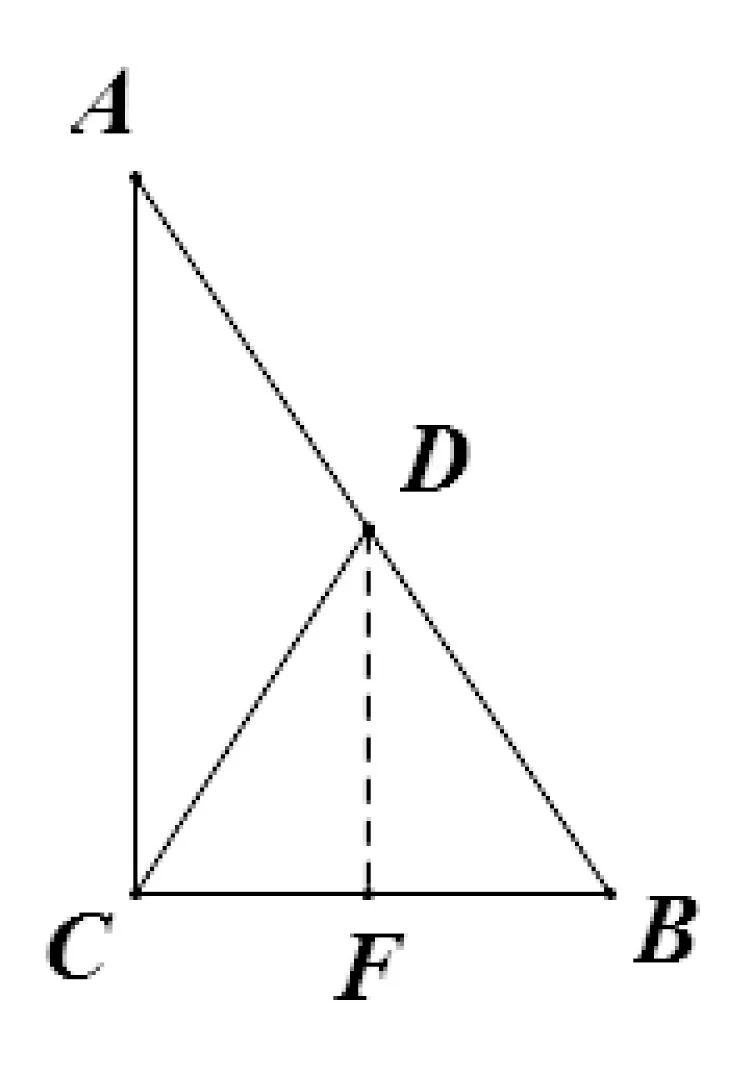
图3

解题思路：由直角三角形斜边中线等于斜边一半可得：CD=BD=3，从而∠DCB=∠DBC，故：sin∠DCB=sin∠DBC=

设计意图：加深对三角函数知识内涵的理解，培养转化思想，形成良好的认知结构。

例3 如图4，在平面直角坐标系xoy中，直线l：y=2x+1 与x轴交于点A，点B在第一象限内且在直线l上，则tan∠BAO=____。

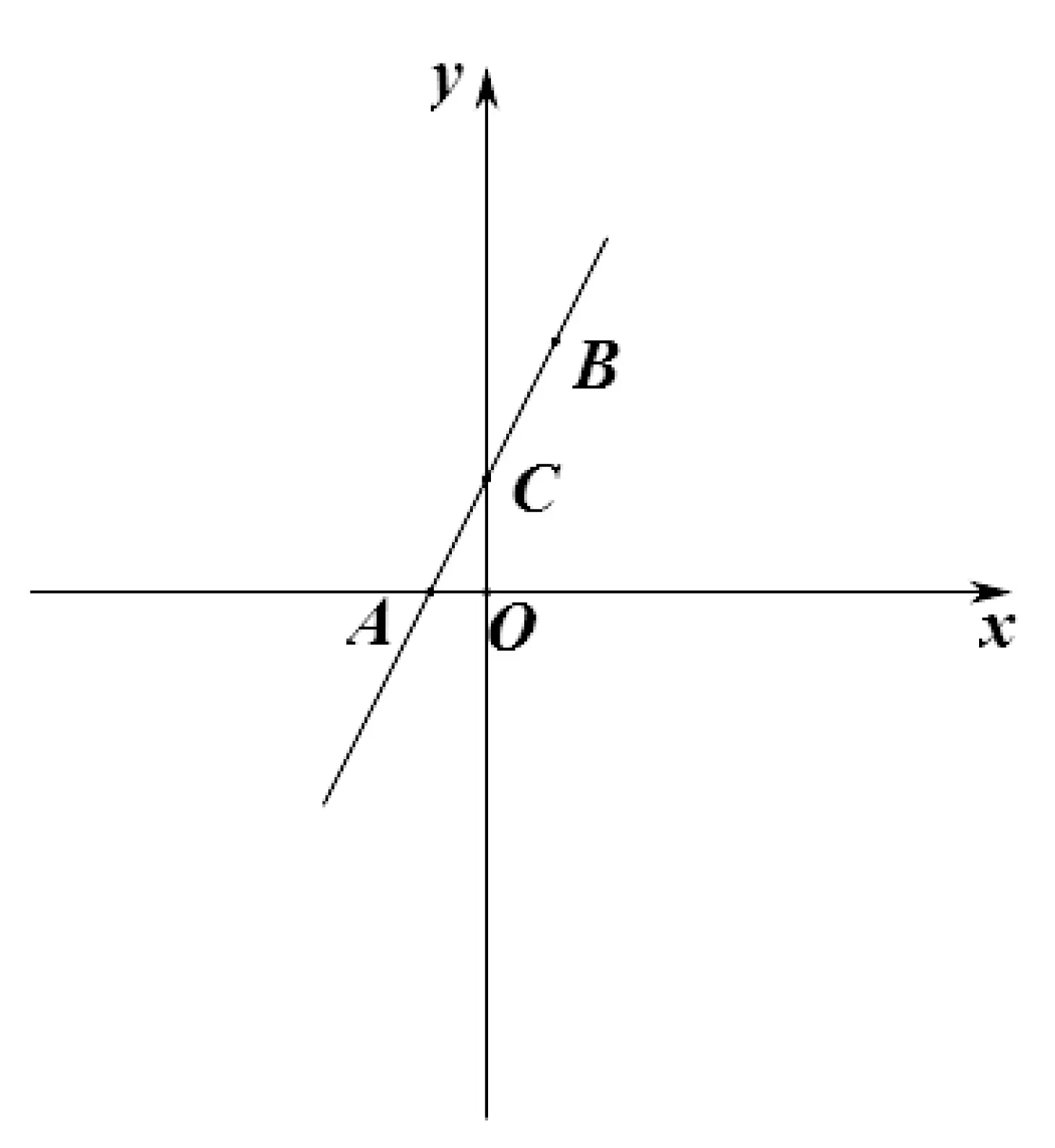
图4

解题思路1：设B点的横坐标为xB，则B点的纵坐标为2xB+1，易得A（-0.5，0），tan∠BAO=

解题思路2：设直线AB与y轴交于点C，易求得A（-0.5，0），C（0，1），tan∠BAO=tan∠CAO=

设计意图：思路1 直接从定义着手，结合代数的思想，通过设点法求出tan∠BAO。思路2 将变化的点B转化为固定的点C，化一般为特殊，直接求出tan∠CAO。通过对比两种方法，形成深刻理解，加深对三角函数定义本质的认识。该题与坐标系结合，初步渗透高中知识中的斜率概念，体现知识的外延性。

（二）知识迁移：深度掌握锐角三角函数理论的工具性及实际应用，注重知识迁移

如何求边或是求角是几何学研究中的一个重要内容，而在初中几何教学中也经常会遇到求边或是求角相关的问题，锐角三角函数的相关知识理论在求边或是求角方面体现了强大的工具性作用。锐角三角函数理论不仅可以解直角三角形也可以用来解一般三角形。即：知道三角形中的某些元素，可以把剩余的元素求解出来。如果一个三角形满足下列条件之一：1.已知三边。2.已知两边一夹角。3.已知两角一边。4.已知两边一对角。这时可以通过三角函数相关知识结合勾股定理求解其余未知元素［2］。求解的一般方法是通过作垂线的方式构造出直角三角形。在读题时一定要注意读透条件，分析三角形中哪些元素已知，如果条件满足上述四种条件之一，该三角形中剩余未知元素即可求解，从而推导出更多的条件，得到的条件越多越有助于问题的分析求解。另外，解三角形到了高中的教学中会学习专门的理论知识，主要是根据余弦定理和正弦定理。注重运用锐角三角函数解决实际生活中的问题，体现了三角函数际应用性。基于上述分析，笔者认为以解三角形作为锐角三角函数理论工具性的核心要点，对知识迁移及应用产生良好的效果，设计了如下单元练习，目的在于提高学生分析问题能力，获得知识应用的深度感悟。培养学生解决实际问题的能力，提高数学建模素养。

例4 在△ABC中，（1）如图5，若AB=4，BC=7，AC=5，则∠B=____cosC=____

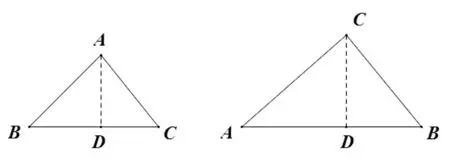
图5

（2）如图6，若cosA=，AB=10，AC=8，则BC=____

图6

解题思路：通过作垂线，将这两个三角转化为直角三角形进行求解。（1）过点A作AD⊥BC，垂足为D，设BD=x，根据勾股定理可列方程-x2=52-（7-x）2，解得：x=4，即BD=4，CD=3，易求得：∠B=45°，cosC=（2）过点C作CD⊥AB，垂足为D，由AC=8，cosA=，求得：AD=6，CD=，BD=4，再由勾股定理求得：BC=

设计意图：本题的两个小题都是为了强化解三角形的一般方法，题（1）可以看成是知道“三边”解三角形，题（2）可以看成是知道“两边一夹角”解三角形。这题亦是为了后续综合性问题作铺垫。让学生深刻理解可以求解三角形的一般条件，当发现问题中的三角形满足上述四个条件之一时，剩余的边、角（或角的三角函数值）就可以求解，从而得到更多条件，有助于问题的求解。从而使学生能应用求解三角形一般方法解决综合性问题。

例5 如图7，某高速公路建设中需要测量某条江的宽度AB，飞机上的测量人员在C处测得A，B两点的俯角分别为45°和30°，若飞机离地面的高度CE为1000 米，且点E，A，B在同一水平直线上，求这条江的宽度AB。

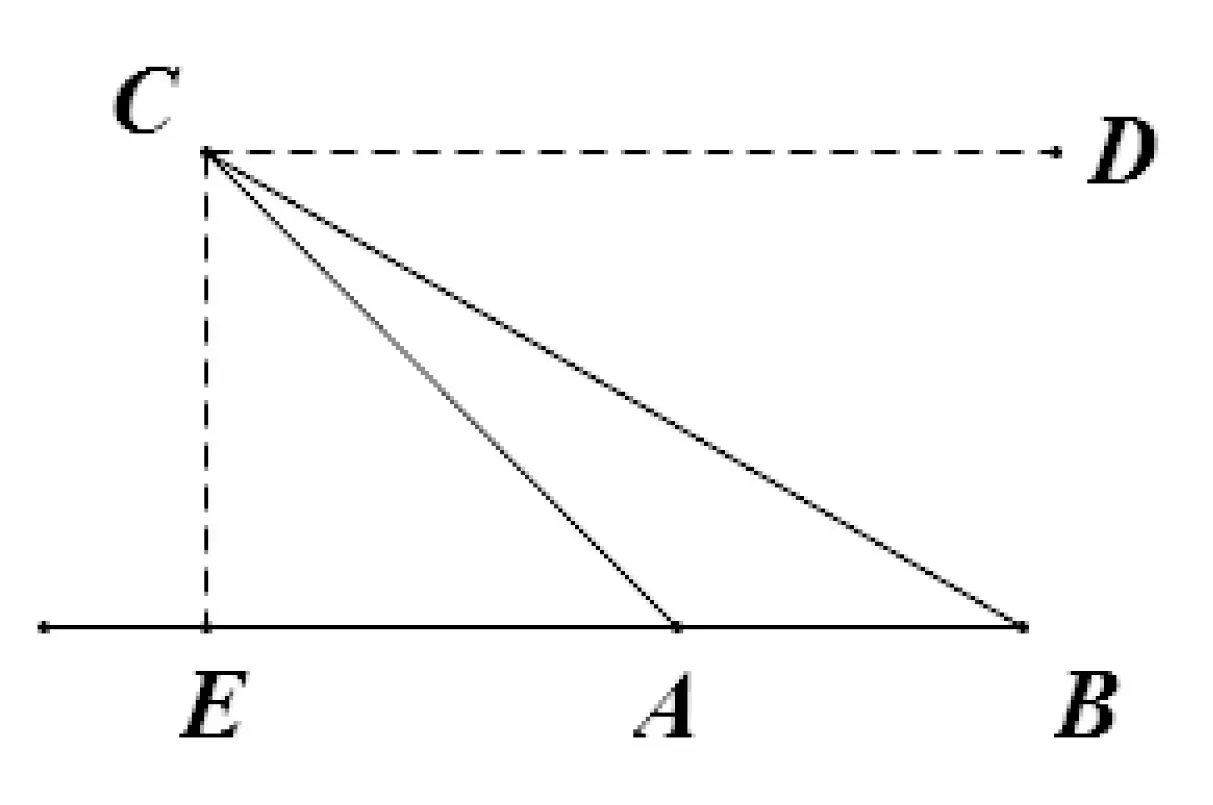
图7

解题思路：作CD//EB，依题得：∠CAE=∠ACD=45°，∠B=∠BCD=30°，通过正切的定义，分别求得：AE=1000，BE=1000从而求得AB=BE-AE=10001000.

设计意图：以实际问题为背景，运用三角函数知识进行求解，体现三角函数实际应用性，培养数学建模素养。

例6 如图8，在△ABC中，BC=AC=10，AB=12，D为AB上一点，过点D作DF⊥AC，延长FD交CB的延长线于点E，求sinE的值。

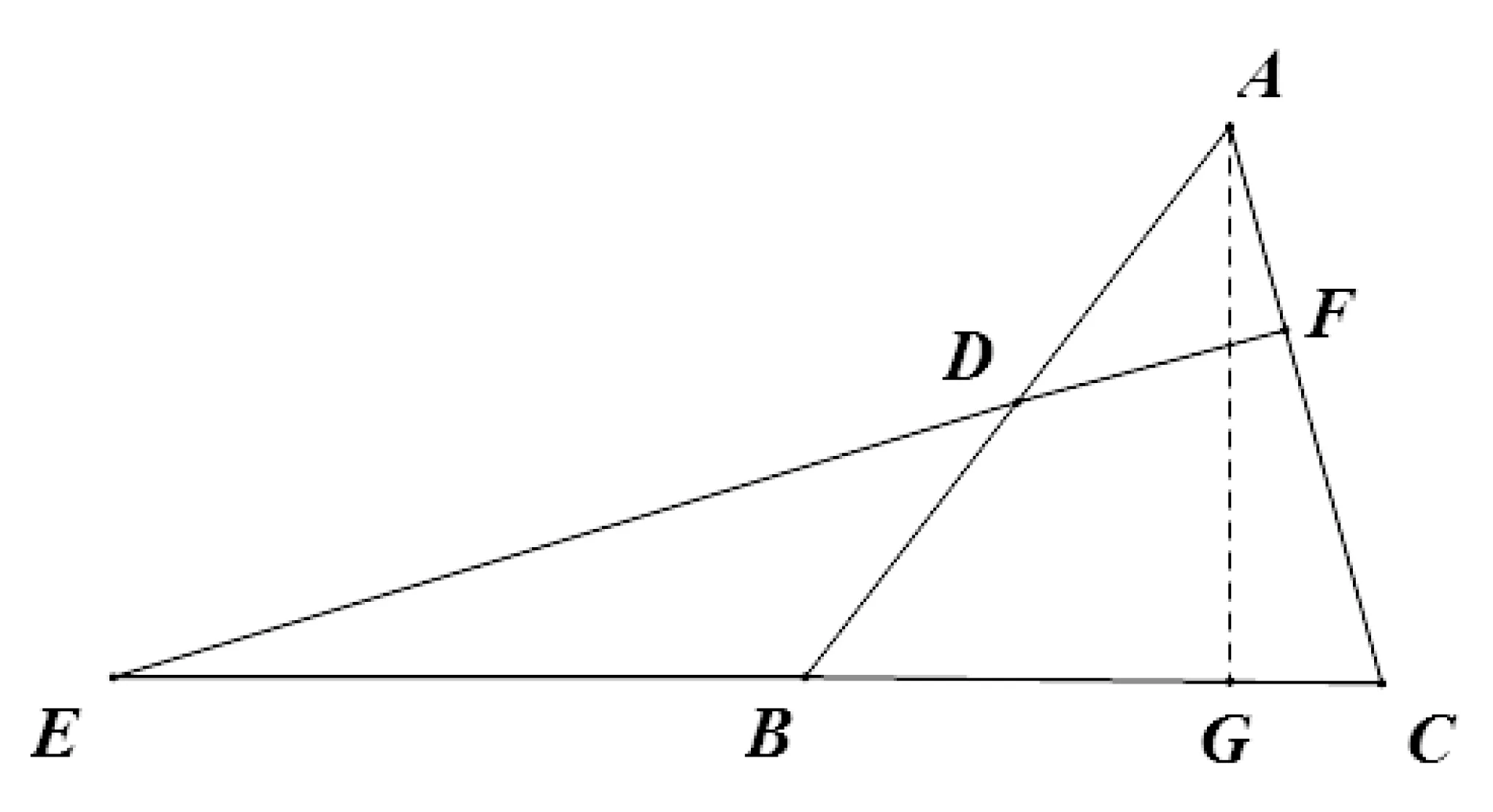
图8

解题思路：△ABC三边已知，故而△ABC其余未知元素均可求解（知三边可解三角形），结合解三角形的理论方法，同例4（1），过点A作AG⊥EC，垂足为G，可得cosC=，又根据∠E与∠C互余，从而求出sinE=

设计意图：该题解题的核心要点在于利用解三角形理论读出更多条件。读题时发现△ABC中三边已知，故而可以通过解三角形的方法求出cosC。该题注重知识迁移运用，培养学生分析问题的能力，完善发展认知结构，加深对三角函数理论工具性作用的理解。

（三）知识整合：深度加强锐角三角函数知识与其他单元之间的综合联系，强化知识整合

锐角三角函数是在九年级下学期进行学习，可以与之前许多单元知识章节产生联系，例如，三角形、勾股定理、圆等章节。笔者以锐角三角函数工具性作为与其他章节结合点，解决相关问题，从而与其产生有机联系，形成知识整合。基于此，设计了如下单元练习，目的在于提高知识的迁移性，培养学生综合运用能力，发展学生高阶思维。

例7 如图9，A，B，C，D是圆O上的点，连接AD，

图9

AB，AC，AD=6，∠DAC=90°，sin∠DBA=求圆的半径r。

解题思路：连接CD，由∠DAC=90°，可知DC 经过圆心O，由∠DBA=∠DCA，得sin∠DBA=sin∠DCA=再根据AD=6，求得CD=10，故r=5。

设计意图：与圆相关知识结合，学会通过弧等则圆周角相等进行“转角”。加深对“角等则三角函数值相等”的认识。

例8 如图10，在△ABC中，∠ACB=45°，AC=BC=10，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE=6，求sin∠BFD的值。

图10

解题思路：结合翻折性质及外角定理发现∠EDC=∠BFD，故sin∠BFD=sin∠EDC，易知CE=4，ED=6，且∠C=45°，对于△CED 已知两边一对角，故可以求出剩余未知的元素，结合解三角形的理论方法，同例4（2）作EM⊥CD，可求得：sin ∠EDC=故sin ∠BFD=

设计意图：该题结合翻折知识，培养学生综合运用能力。不易直接求得∠BFD的正弦值，发现∠BFD=∠CDE，从而将问题转化为求解sin∠CDE，从解三角形的眼光来看，在△CED中，CE，ED，∠C是已知的，知道了两边一对角，从而可求出sin∠CDE。培养转化思想及挖掘隐含条件的能力；培养高阶思维，加强学生对“解三角形”相关知识的应用能力。

三、反思与总结

本文以《锐角三角函数》为例阐述了笔者基于深度学习理论下单元作业设计的理念。深度学习理论下单元作业设计一定要结合学生的具体学情，全方位思考单元作业设计的有效性，细致地整理单元知识要点、思想方法，找出知识的串联点，体现知识理论工具性及实际应用性，引导学生全面系统的认识，引发学生深层次地思考，丰富学生的学习体验，培养学生良好的学习习惯，从而实现核心素养的养成。