基于均匀化理论的混凝土等效弹性模量预测
2022-06-16陈思翰吕方涛王玲玲孔德文
陈思翰,吕方涛,黄 威,王玲玲,孔德文
(贵州大学土木工程学院,贵阳 550025)
0 引 言
混凝土作为一种典型的非均质复合材料,其宏观力学性能由其细观乃至微观结构决定。因此,只有从细观尺度出发,深入研究混凝土材料在细观层次的组成和排列结构的作用与内在联系,从局部到整体,从细观到宏观,才能更清楚地把握混凝土材料的力学性能[1]。Roelfstra等[2]在混凝土材料力学性能的研究中引入“细观”这一概念,将混凝土视为由骨料、水泥砂浆及二者间界面构成的三相复合材料。借鉴细观尺度的研究思想,国内外学者开展了诸多研究,逐渐发展形成了混凝土细观力学,并建立了细观力学及多尺度模拟的数值实现方法,利用数值结果揭示混凝土材料细观成分对其宏观力学特性的影响规律及作用机理。
弹性模量是反映混凝土材料力学性能的重要指标,用于研究混凝土材料变形、裂纹开裂和扩展及损伤等。因此,弹性模量的确定是研究混凝土力学性能的关键环节。在细观模型应用方面,刘光廷等[3]提出了随机骨料模型,用于表征混凝土中骨料的空间随机分布情况,为后续研究提供了基础。Christensen等[4]建立两相模型,用于预测复合材料的等效弹性模量,但未考虑界面过渡区的影响。Nilsen等[5]研究表明,骨料-水泥砂浆间界面过渡区对混凝土的等效弹性模量存在一定影响。为更准确预测混凝土的弹性模量,Neubauer等[6]提出了考虑界面层影响的混凝土细观模型。在理论研究方面,复合材料弹性性能的预测分析方法主要包括代表体元法、工程经验公式法、自洽法及均匀化理论等。其中,代表体元法与工程经验公式法简单易行,但代表体元法的误差难以预测且不具备严格的数学理论,工程经验公式法则缺乏普适性,预测效率较低[7]。自洽法的应用对象为结构简单的复合材料,研究对象为结构复杂的复合材料时,表现出计算量较大的缺点。而均匀化理论是一种量化复合材料微观结构与其宏观性能之间联系及相互作用的多尺度分析方法,应用严格的理论基础研究复合材料微观结构与宏观性能的关系[8]。唐欣薇等[9]从细观尺度出发,基于均匀化理论研究了混凝土的宏观力学性能,宏细观结果具有较好的一致性。邓方茜等[10]采用均匀化理论,预测纤维混凝土的弹性模量,预测值与试验值吻合较好。Ouyang等[11]基于细观模型,运用均匀化理论研究了混凝土细观组分与弹性模量的关系。综上所述,基于混凝土真实结构,建立与其对应的细观模型,采用多尺度分析方法可较好预测混凝土的宏观力学特性,是量化细观组分对混凝土宏观结构力学性能影响程度的可靠研究方法。
本文将混凝土视为由骨料、水泥砂浆及两者间界面过渡区组成的三相复合材料,采用瓦拉文公式实现骨料级配选取,运用蒙特卡罗方法完成骨料的随机生成与投放,建立具有周期性的混凝土单胞模型,利用Python自动施加周期性边界条件,结合均匀化理论,提出混凝土等效弹性模量的预测方法;基于混凝土单胞模型,通过控制变量法研究单胞尺寸、骨料体积率、骨料最大粒径和界面层厚度对混凝土等效弹性模量的影响规律。
1 单胞模型的建立
1.1 骨料级配
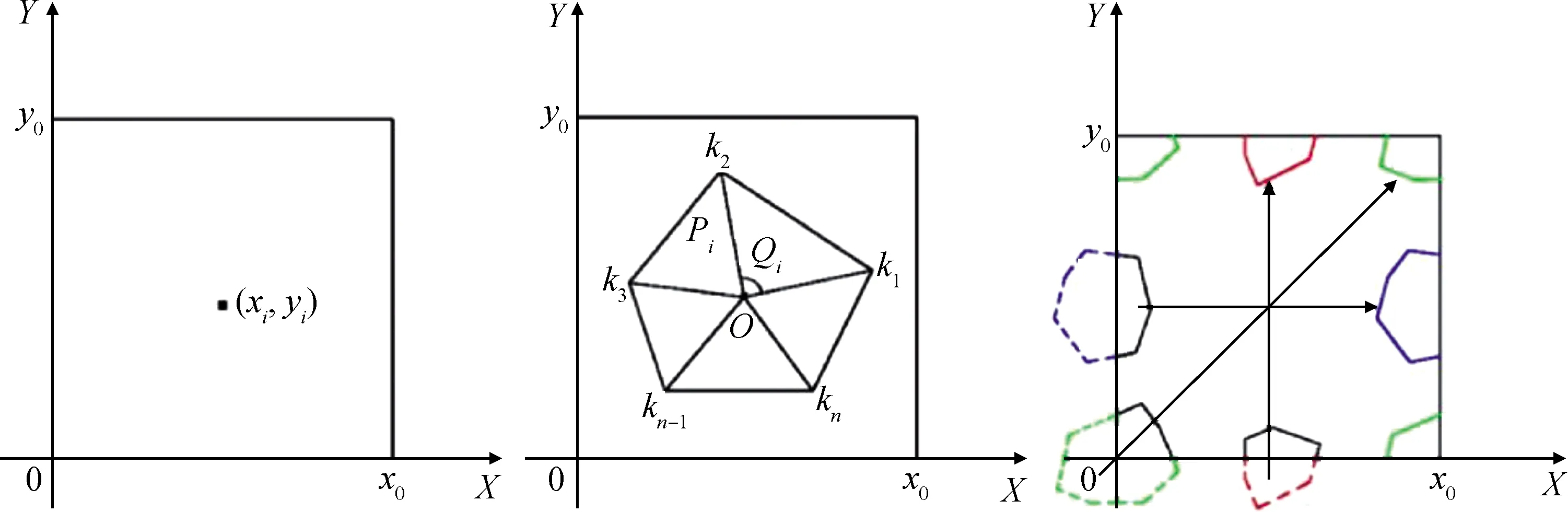
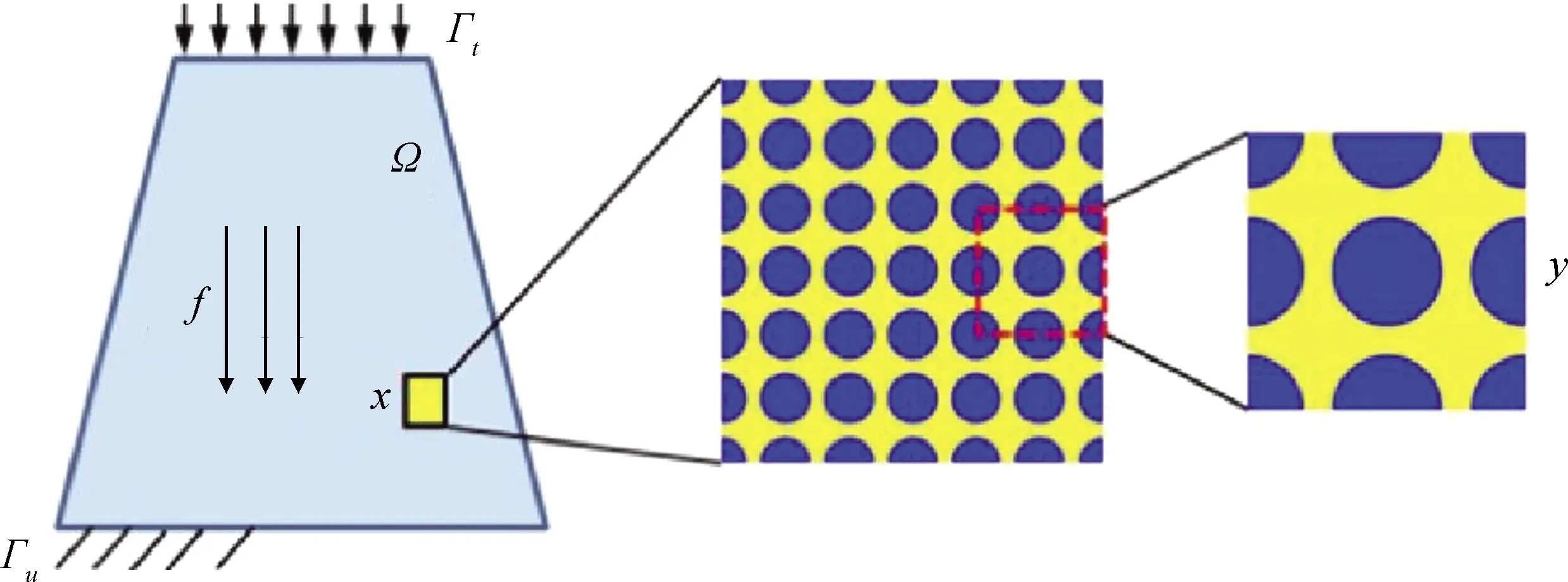
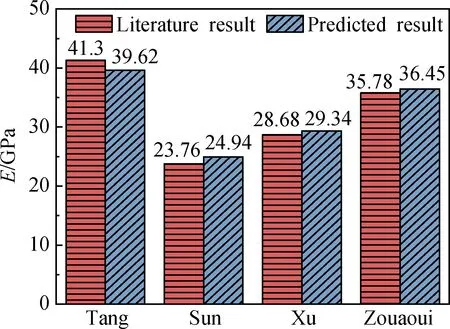
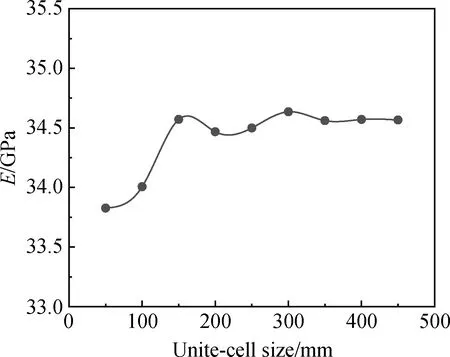
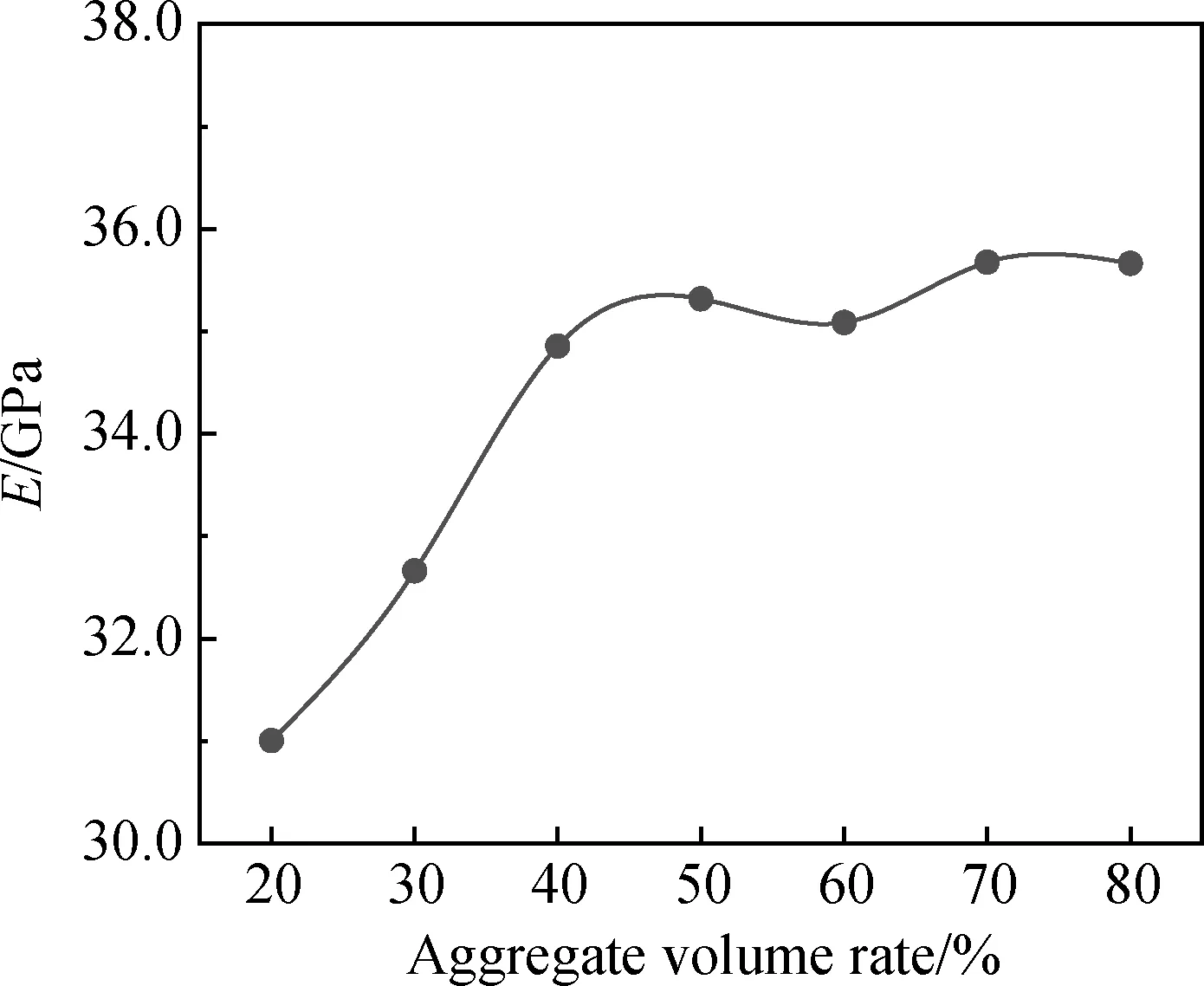
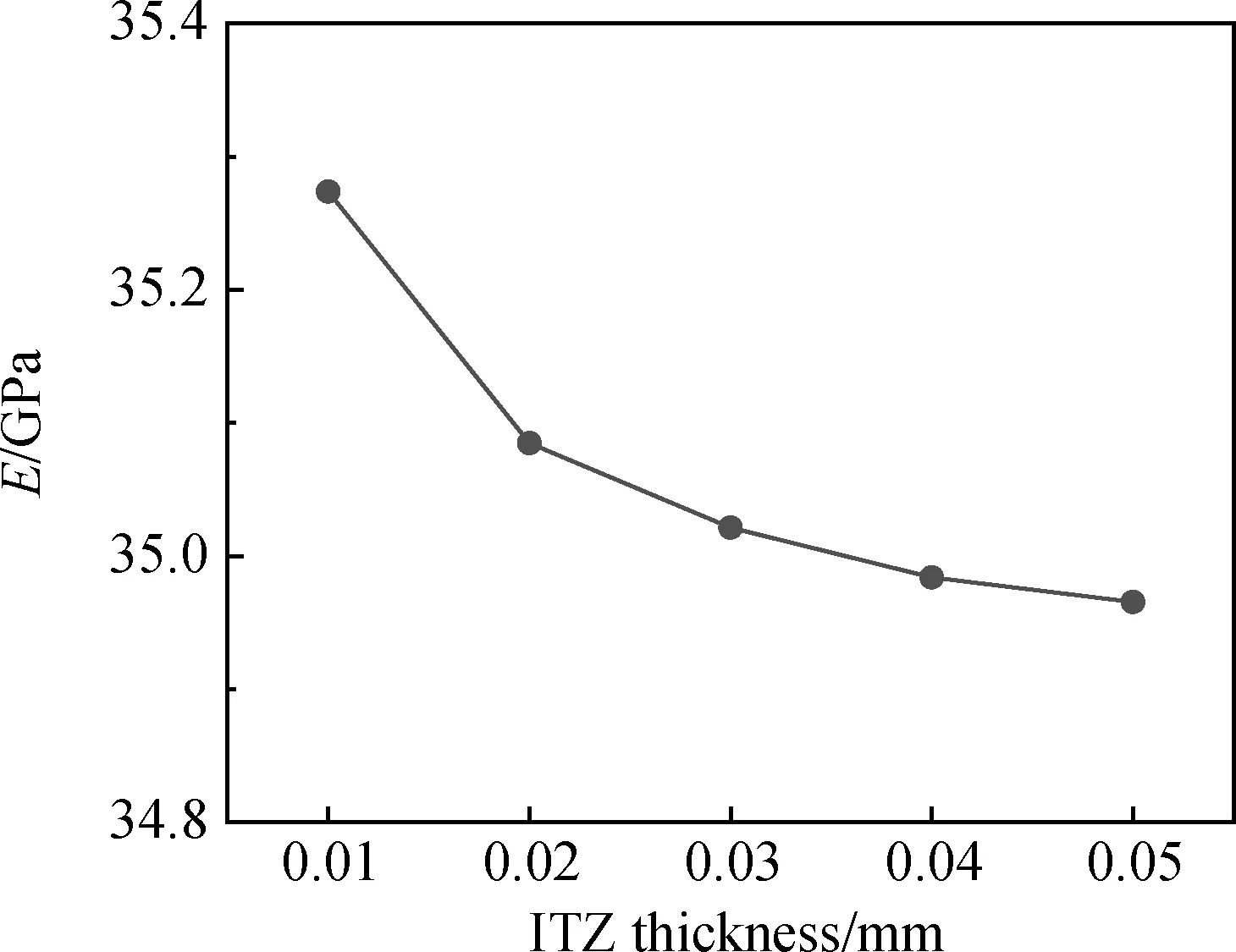
为使混凝土产生最优的结构密度和强度,通常采用富勒曲线表示混凝土的骨料粒径分布。富勒曲线是针对三维空间中的骨料而言的,然而三维模拟较为复杂,计算量巨大。Walraven等[12]基于概率统计提出了富勒曲线的二维转化公式,将其转化为混凝土内截面上任一点具有骨料直径D (1) 式中:D0为筛孔直径;Pk为混凝土中骨料的占比;Dmax为混凝土中骨料的最大粒径。 混凝土细观建模的原则是尽可能准确地反映混凝土的真实结构,表现骨料形状的不规则性及骨料位置分布的随机性。本文基于蒙特卡罗方法,利用Python的random模块,实现随机多边形骨料的生成与投放,如图1所示。骨料的生成到投放分为三个步骤: (1)确定中心坐标。在边长为x0、y0的矩形区域内随机生成一点(xi,yi),作为骨料衍生的中心坐标。 (2)建立随机多边形骨料。根据粒径范围控制骨料顶点与中心坐标之间的距离Pi,以随机角度Qi生成n(5≤n≤9)个顶点k,连接各顶点构成多边形骨料。 (3)判断骨料与模型边界的相对关系。若骨料位于模型内部,则不做处理;若骨料超出模型边界,则删除该骨料;若骨料与模型边界相交,则对骨料进行切割,并将超出边界的部分置于边界的中心对称处,实现骨料的周期性分布。 图1 骨料的生成与投放Fig.1 Generation and delivery of aggregate 建立由骨料、水泥砂浆及两者间界面过渡区构成的混凝土单胞模型,如图2所示。运用瓦拉文公式确定混凝土的粒径分布,采用蒙特卡罗方法实现随机多边形骨料的生成与投放,建立具有周期可重复性的单胞模型,即可由许多个微观单胞模型重复堆叠构成宏观层次的模型。因此,混凝土单胞模型的有效性质可用于表征混凝土的有效性能。 图2 单胞模型示意图Fig.2 Schematic diagram of unite-cell model 均匀化理论是研究周期性细观结构的一套严格的数学理论。它以构成材料细观结构的单胞为研究对象,将宏观结构中一点的位移、应力等物理量采用摄动解的形式,展开为与细观结构相关摄动量的渐进级数,利用虚功原理得到单胞的平衡方程,再引入单位荷载和边界条件,通过相关数学变换得到单胞的等效弹性模量。 设在空间R3中占据体积Ω的混凝土材料结构如图3所示,结构体受体力f,在边界Γt上受表面力t,Γu上给定位移u。对于非均质复合材料,其宏观结构受外力作用时,应力和位移等场变量随宏观位置的改变而改变,而细观结构的高度非均匀性导致这些场变量在宏观位置的微小领域内产生剧烈变化。对于此类双尺度问题,可引入小参数ε(0<ε≪1),令y=x/ε,其中y为细观坐标,x为宏观坐标,1/ε为放大因子。 假设所有变量均建立于宏、细观双尺度基础上: Φε(x)=Φ(x,y) (2) 式中:ε表示该函数具有双尺度的特征。 假设单胞模型满足下列边界条件及三大基本方程: 力边界条件: (3) 位移边界条件: (4) 平衡方程: (5) 几何方程: (6) 本构方程: (7) 图3 周期性单胞示意图Fig.3 Schematic diagram of periodic unite-cell 采用渐进开展方法,将任一点位移uε(x)展开为: uε(x)=u0(x,y)+εu1(x,y)+ε2u2(x,y)+… (8) 由虚功原理可得: (9) 式中:u为单胞的位移;v为边界条件下的虚位移。 将式(8)代入式(9)可得到关于u0、u1的摄动方程,根据周期函数的性质,通过相关的数学变换,可得出单胞的等效弹性模量: (10) 对单胞等效弹性模量的求解,现已有多种方法可以选择,考虑到计算成本,本文选择引入周期性边界条件,在周期性边界条件下对单胞施加不同的初应变进行求解。单胞的周期性边界条件可表述为: (11) 对此,可通过建立单胞节点、对边的线性约束方程来施加周期性边界条件。为提高混凝土弹性模量预测模型的计算效率,采用Python编写周期性边界条件自动施加程序,加快单胞等效弹性模量的计算速度。由于在单胞模型分析中,应力边界条件属于自然条件,所以对于周期性边界条件的施加仅需考虑位移边界条件。在图4模型四个角点和两条对边建立位移约束条件,约束方程具体如下: 角点位移约束方程: (12) (13) (14) (15) 边位移约束方程: (16) (17) 根据位移约束方程,可将周期性边界转化为: (18) 式中:+、-表示对称边界。 图4 单胞几何图Fig.4 GeometricFigure of unite-cell 为验证本文建立的混凝土单胞模型的有效性与方法的准确性,采用已有文献组分材料属性数据(见表1)预测混凝土等效弹性模量。 表1 各组分材料属性Table 1 Material properties of each component 图5 等效弹性模量结果对比[13-16]Fig.5 Comparison of equivalent elastic modulus results[13-16] 建立3种骨料随机分布的单胞模型,施加周期性边界条件,预测混凝土材料的等效弹性模量,取3个等效弹性模量预测值的平均值与对应文献结果进行比较,对比结果如图5所示。预测值与文献值吻合度较高,两者最大误差为4.97%,最小误差为1.87%。对误差最大的一组数据进行分析可知,Sun等[14]建立的细观模型,骨料为圆形,采用的分析方法为Mori-Tanaka法,不同的分析方法与骨料形状是产生相对较大误差的主要原因。经已有文献验证,本文建立的混凝土单胞模型可用于混凝土材料等效弹性模量的预测。 采用细观模型预测混凝土等效弹性模量时,可以定量地研究各组分因素对等效弹性模量的影响规律。引用文献[17]中的材料参数:骨料弹性模量EA=55.4 GPa,泊松比μ=0.16;水泥砂浆弹性模量EM=25.7 GPa,泊松比μ=0.22;界面过渡区弹性模量EI=23.6 GPa,泊松比μ=0.16。利用本文建立的混凝土单胞模型,讨论单胞尺寸、骨料体积率、界面层厚度及骨料最大粒径对混凝土等效弹性模量的影响规律。 单胞模型存在某个周期可用于表征混凝土的宏观性能:周期过小时扰动较大,不能充分表征混凝土的宏观性能;周期过大时趋于稳定,但计算量巨大。因此,需要确定能准确反映混凝土宏观性能且计算成本低的单胞尺寸。基于本文建立的预测模型,生成9组不同单胞尺寸的、级配合理的、骨料体积率为40%的混凝土细观模型,其中每组包括3种骨料分布。 图6为单胞尺寸对等效弹性模量的影响。从图6中可以看出,单胞尺寸小于150 mm时,混凝土等效弹性模量随单胞尺寸的增加而增大,单胞尺寸超过150 mm后,等效弹性模量围绕某一值上下波动,并随着单胞尺寸的持续增大,振荡反应逐渐变小,最终趋于某个稳定值。因此,能充分反映混凝土宏观性能且计算成本低的单胞尺寸为150 mm。后续研究以边长150 mm建立单胞模型,分析骨料体积率、界面层厚度与骨料最大粒径对混凝土等效弹性模量的影响。 图6 单胞尺寸对等效弹性模量的影响Fig.6 Effect of unite-cell size on equivalent elastic modulus 图7 骨料体积率对等效弹性模量的影响Fig.7 Effect of aggregate volume rate on equivalent elastic modulus 为探究骨料体积率对混凝土等效弹性模量的影响规律,分别建立骨料体积率为20%、30%、40%、50%、60%、70%、80%的单胞模型,结果如图7所示,骨料体积率小于40%时,等效弹性模量随骨料体积率的增加快速增大,超过40%后,增长幅度变缓,等效弹性模量在35 GPa左右波动。骨料体积率从20%提高至80%时,混凝土等效弹性模量提高约15%。 混凝土中骨料-水泥砂浆间界面过渡区(interfacial transition zone, ITZ)对其等效弹性模量存在一定影响,因此,有必要研究界面层对混凝土等效弹性模量的影响规律。本文以界面层厚度为研究对象,参考已有研究[18]成果,界面层厚度分别取0.01 mm、0.02 mm、0.03 mm、0.04 mm和0.05 mm,骨料体积率取40%,建立相应的混凝土单胞模型,等效弹性模量预测结果如图8所示。 图8表明界面层厚度对混凝土等效弹性模量的影响呈单调递减的趋势。界面层厚度由0.01 mm增加至0.05 mm时,等效弹性模量由35.27 GPa减小到34.97 GPa,降幅约为0.85%,可见,界面层厚度对混凝土等效弹性模量的影响较小。 取骨料体积率为40%,骨料最小粒径为5 mm,骨料最大粒径为25 mm至40 mm,建立单胞预测模型,研究骨料最大粒径对等效弹性模量的影响规律,结果如图9所示。结果显示混凝土等效弹性模量随骨料最大粒径的增加而增大,呈单调递增的变化趋势。骨料最大粒径小于30 mm时,对等效弹性模量的影响较小,超过30 mm后,对等效弹性模量的影响相对较大。骨料最大粒径从25 mm增大至40 mm时,混凝土等效弹性模量提高约1.86%,影响不显著。 图8 界面层厚度对等效弹性模量的影响Fig.8 Effect of ITZ thickness on equivalent elastic modulus (1)本文建立的混凝土单胞模型考虑了骨料-水泥砂浆间界面层的影响,能比较真实准确地预测混凝土的等效弹性模量。 (2)单胞尺寸对混凝土等效弹性模量的影响结果表明,可充分表征混凝土等效弹性模量且计算成本低的单胞尺寸为150 mm。 (3)骨料体积率位于20%~40%内时,对混凝土等效弹性模量的影响显著,随着骨料体积率增大,弹性模量逐渐增加。当骨料体积率从20%提高至80%时,混凝土等效弹性模量提高约15%。 (4)界面层厚度与骨料最大粒径对混凝土等效弹性模量的影响均不明显。界面层厚度对等效弹性模量的影响规律呈单调递减的变化趋势,界面层厚度从0.01 mm增大到0.05 mm时,等效弹性模量降幅约为0.85%。随着骨料最大粒径的增加,等效弹性模量逐渐增大,骨料最大粒径从25 mm增大到40 mm时,混凝土等效弹性模量提高约1.86%。1.2 骨料生成与投放
1.3 单胞模型

2 理论分析方法
2.1 均匀化理论
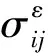

2.2 周期性边界条件
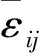


3 模型验证

4 等效弹性模量影响因素
4.1 单胞尺寸
4.2 骨料体积率
4.3 界面层厚度
4.4 骨料最大粒径
5 结 论
