沿海混凝土结构氯离子对流区深度计算模型

郝 磊，陈 峰，彭文锋，查 斌

(1.长安大学公路学院，西安 710064；2.在役长大桥梁安全与健康国家重点实验室，南京 211112)

0 引 言

沿海地区存在的大规模混凝土基础设施都面临严峻的氯离子侵蚀问题，其会影响混凝土结构的耐久性甚至安全性，因此引起了广泛的关注与讨论。Collepardi等[1]率先提出借助Fick定律解释混凝土内部氯离子扩散传输的现象，经众多学者[2-3]研究发现，处于饱水状态的混凝土，其内部氯离子传输状态可以通过Fick第二定律较好的展现。

干湿交替环境中，混凝土内部维持非饱水状态，此时氯离子不但以扩散作用进入混凝土，还会受到对流效应的影响。混凝土构件在与外界水相接触的瞬间，表面将主要发生由毛细吸附水形成的对流，在水分流动的过程中将携带大量氯离子，从而导致定向迁移。然后在湿度梯度的影响下，氯离子以非饱和渗流的方式，不断侵入混凝土。

处于干湿交替环境中的混凝土构件，其钢筋锈蚀问题最为严重，因此研究混凝土处于干湿交替环境中其内部氯离子的传输规律具有重要价值。於德美等[4]结合水分扩散与稀物质传输方程，得到了以混凝土内部水分饱和度为基本变量的氯离子传输方程。申林等[5]根据水分迁移的特点，推导出氯离子传输的对流扩散耦合方程，利用细观随机混凝土模型研究了骨料对混凝土内部氯离子分布情况的影响。李荣涛[6]基于有限元方法建立了多相耦合的氯离子侵蚀模型。

上述研究主要通过求解由偏微分方程组组成的计算模型来描述干湿交替环境中氯离子的传输过程，虽然能从机理上反映氯离子的传输，但实际桥梁结构服役时间一般高达数十年，采用这样的模型进行计算用时较长，难以直接指导混凝土结构耐久性设计。考虑到使用方便和计算简明，国内外研究者仍倾向使用Fick第二定律的解析方程来描述在非饱和态下混凝土内部氯离子传输情况。

混凝土的低渗透性特点，使得其内部的水输送与外部环境变化存在滞后现象。干湿交替的自然条件仅能在混凝土表面有限深度范围内产生影响，该深度可定义为氯离子传输的对流区深度Δx。基于该假定，Andrade等[7]、Matthews等[8]、陆春华等[9]将混凝土氯离子分布区域分为对流区和扩散区两个部分，通过Δx对Fick第二定律解析解进行修正，整理得到简化计算模型来预测干湿交替环境混凝土中的氯离子传输行为。

在该模型中，虽将混凝土中的氯离子传输分为对流区和扩散区，但主要造成影响的是内部的扩散作用，即描述Δx深度范围以外的氯离子浓度。模型的适用性很大程度上取决于对流区深度及模型中重要技术参数的合理取值。

Duracrete等[10]根据结构维修成本，结合环境特征给出了混凝土结构不同服役环境对应的Δx经验取值。冯超等[11]研究发现由于干湿循环次数的增多，对流区深度会趋于稳定，根据干湿循环90次的氯离子传输计算结果，以干湿循环周期为自变量，得到计算对流区深度的方程。Gao等[12]通过对270个试验样本假设检验，得出对流区深度满足耿贝尔分布，均值等于3.99 mm。高延红等[13]根据对自然潮差环境的现场测试成果，总结出对流区深度的随机性可用正态分布描述，均值为3.76 mm。庞森等[14]使用数值方法求解，得到饱和度峰值位置不断向混凝土深处移动，并最终稳定在20 mm深度左右。崔钊玮等[15]设计试验来模拟浪溅区混凝土构件的服役状况，考虑包括混凝土开裂、干湿循环和氯盐环境等因素，发现氯离子分布曲线在10～15 mm范围内出现峰值。

综上所述，对流区深度Δx是修正Fick第二定律简化计算模型的关键参数，即当Δx确定后，氯离子的侵蚀问题就可以简化为用饱和混凝土扩散方程进行近似求解。然而目前有关Δx取值的规定尚未成熟，大多依据短期试验测试与经验判断直接将其假定为定值，忽略了温度、混凝土材料构成、湿度等因素的影响，对简化计算的精度产生较大误差。因而，深入研究对流区深度将是提高简化计算模型准确度的关键。本文在建立混凝土细观尺度求解模型的基础上，综合考虑水分迁移、氯离子传输和温度场等因素，建立了干湿交替区域混凝土细观尺度氯离子侵蚀计算模型，对Δx在各显著影响因素变化下反映出的规律进行分析，给出了考虑服役时间、日平均气温和干燥湿润时间比等影响参数的对流区深度Δx时变计算模型，以期对干湿交替环境中混凝土氯盐侵蚀简化计算模型进行精确求解提供参考。

1 非饱和混凝土氯离子传输数值模拟计算模型

在浓度梯度的驱动下，氯离子从外界环境向混凝土内部扩散，同时随着混凝土孔隙结构中水分的自由移动而发生对流，特别是当混凝土表面干燥时，水分蒸发使得氯离子在向内部扩散的同时也向表层聚集，此区域范围氯离子侵蚀整体呈现非饱和混凝土传输特征。以混凝土细观骨料模型为基础，引入水分迁移模型、氯离子传输模型和环境温度场模型来讨论干湿交替区域氯离子传输的规律将是精确分析该传输模式的更为有效的方法。

1.1 细观骨料模型

比较于宏观与微观尺度，细观尺度的有限元模型既可以充分考虑混凝土内部非均质的特性，也揭示了其内部构造和宏观力学特征、扩散和渗透特征间的相互关系，同时计算量也比微观尺度小。所以，从细观尺度上模拟混凝土的非均质性，已被大部分研究者认可[16]。

本文为考虑混凝土非均质性对氯离子传输的影响，建立了细观分析模型。细观尺度下，混凝土一般被看作是粗骨料、水泥和二者之间的界面过渡区(interfacial transition zone， ITZ)组成的多相复合物。由于ITZ厚度相对小，并且氯离子透过分界层时的扩散量也更少，所以，在该计算模型中暂不考虑对骨料边界层的影响。同时，由于混凝土中大部分的粗骨料都很密实，氯离子很难扩散进入其中，因此可假定粗骨料中氯离子的扩散系数为零。为研究方便，本文假定混凝土由粗骨料和砂浆组成，取局部样本研究尺寸为100 mm×100 mm，使用AutoCAD软件按照混凝土试样照片绘制二维混凝土细观骨料有限元模型，如图1所示。

图1 混凝土样本细观骨料模型Fig.1 Meso-aggregate model of concrete samples

1.2 干湿交替分析模型

水分本身作为氯离子传输的主要介质，在流动的同时也会搬运侵蚀性物质。所以，在混凝土结构性能的长期演化过程中，了解水分在混凝土中的储存和运移规律具有举足轻重的意义。

非饱水状态的混凝土与外部环境水相接触的瞬间，其表面以毛细作用吸收水分，进而在湿度梯度的影响下，以非饱和渗流的形式向混凝土内输送，这一过程可用扩展的Darcy定理[17]来解释，水分渗流速度(Js)可表示为：

(1)

式中：Dm为水分扩散系数，m2/s；x为扩散深度，mm；s为混凝土含水饱和度。

处于干湿交替区域的混凝土构件，其内孔隙饱和度将保持非平衡状态，并由此产生了湿度梯度场，在场的驱动作用下混凝土内部氯离子通过扩散和对流的方式迁移。氯离子在非饱和状态下的输运过程可用对流扩散方程说明：

(2)

式中：C为氯离子浓度(占混凝土质量百分数)，%；Deff为氯离子在饱水混凝土中的扩散系数，m2/s。

(3)

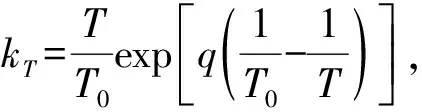
公式(2)为二阶偏微分方程，通过分析混凝土结构服役的自然环境状况，可以确定出计算模型的初始条件和边界条件，之后可以借助有限元法近似求解。水分传输和氯离子迁移以耦合的方式存在，因此对于二者的边界条件需同时定义。从结构长期服役来看，自然环境中的干湿交替条件可视为等周期干燥和湿润交替过程，即较长时间周期内可认为干燥阶段、湿润阶段时间趋于稳定。各阶段传输方式如式(4)、(5)所示。

混凝土处于干燥阶段时，水分能够在混凝土表面自由交换，而氯离子则不能从混凝土表面进入大气环境。

(4)

式中：RH为空气相对湿度；r为饱和度修正系数；u为水分对流速度。

湿润阶段混凝土边界处于饱水状态，可认为表层混凝土孔隙液内的氯离子浓度与构件表面积聚的氯离子浓度Cs(t)相等。

(5)

1.3 环境温度场模型

不同温度条件下水分子和氯离子的活化能有所不同，而气温的波动也会对水分扩散以及氯离子迁移造成影响。目前有关耐久性的研究主要以某一区域的环境平均温度代替结构实际温度场，但实际混凝土结构内部温度分布往往随时间和空间的变化存在差异，表现为非恒定的值。

根据能量守恒定律，混凝土结构导热过程可用Fourier方程[18]表示：

(6)

式中：ρ为混凝土密度；c为混凝土比热容；Φ为混凝土内部热源。

地球因存在自转和公转现象，形成了太阳辐射能量的周期性变化，本文将自然环境温度变化简化为正弦函数形式表示，变化周期为24 h[19]：

(7)

式中：Tav为日平均气温，K；Tam为气温日变化幅值，K。

1.4 非饱和混凝土氯离子传输计算分析

基于COMSOL软件建立非饱和混凝土氯离子传输分析数值计算模型，综合考虑了水分迁移、氯离子传输和温度变化的影响，并以文献[20]的试验数据作为计算分析对象验证模型的有效性。文献[20]中G3S1试验组数据中的Cl-含量峰值及对流区深度现象明显，便于验证对流计算结果，故选取该组试验条件进行数值分析，试验中试件尺寸为100 mm×100 mm×400 mm，混凝土的强度等级为C30，水灰比为0.49，除腐蚀面外其他各面均用环氧树脂密封，保证氯离子沿一维方向输运。G3S1试验组单次循环持续48 h，干湿时间比为3 ∶1，具体的试验方案见表1。

表1 干湿循环试验方案Table 1 Dry-wet cycle experiment scheme

在模拟计算试验过程时，按照试验设计参数进行干湿交替及温度场循环，每个干湿过程的求解结果作为下一个干湿循环过程的初始条件。整个试验过程中混凝土内部氯离子分布的时空变化情况即可通过求解给出明确的分析结果，循环100 d时混凝土内部氯离子分布情况如图3所示。湿润阶段随着混凝土内部达到饱水状态，在浓度梯度促使下环境溶液中的氯离子会逐渐向混凝土深处迁移。混凝土表层水分在外界环境干燥时会逐渐蒸发，由此引起的对流作用使得混凝土浅层区域的氯离子出现反向传输，随着内部孔隙液的蒸发不断向表面转移。表层混凝土内的氯离子在干湿交替的循环过程中持续累积，同时更深层区域的氯离子在扩散作用下仍保持着向内部传递。

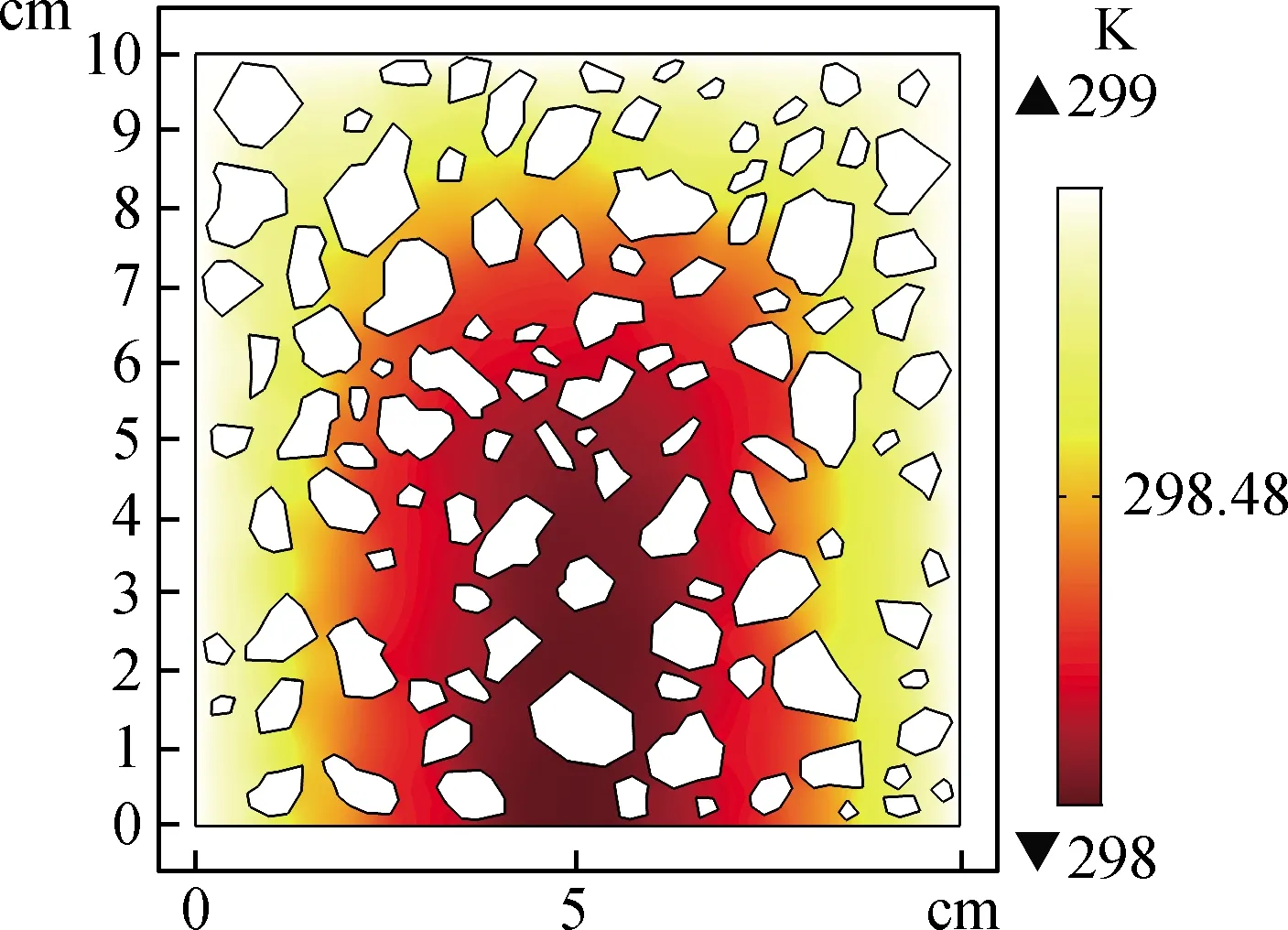
图2 混凝土内部温度场示意图Fig.2 Schematic diagram of temperature field in concrete

图3 循环100 d时混凝土内部氯离子分布示意图Fig.3 Schematic diagram of distribution of chloride ion in concrete after 100 d

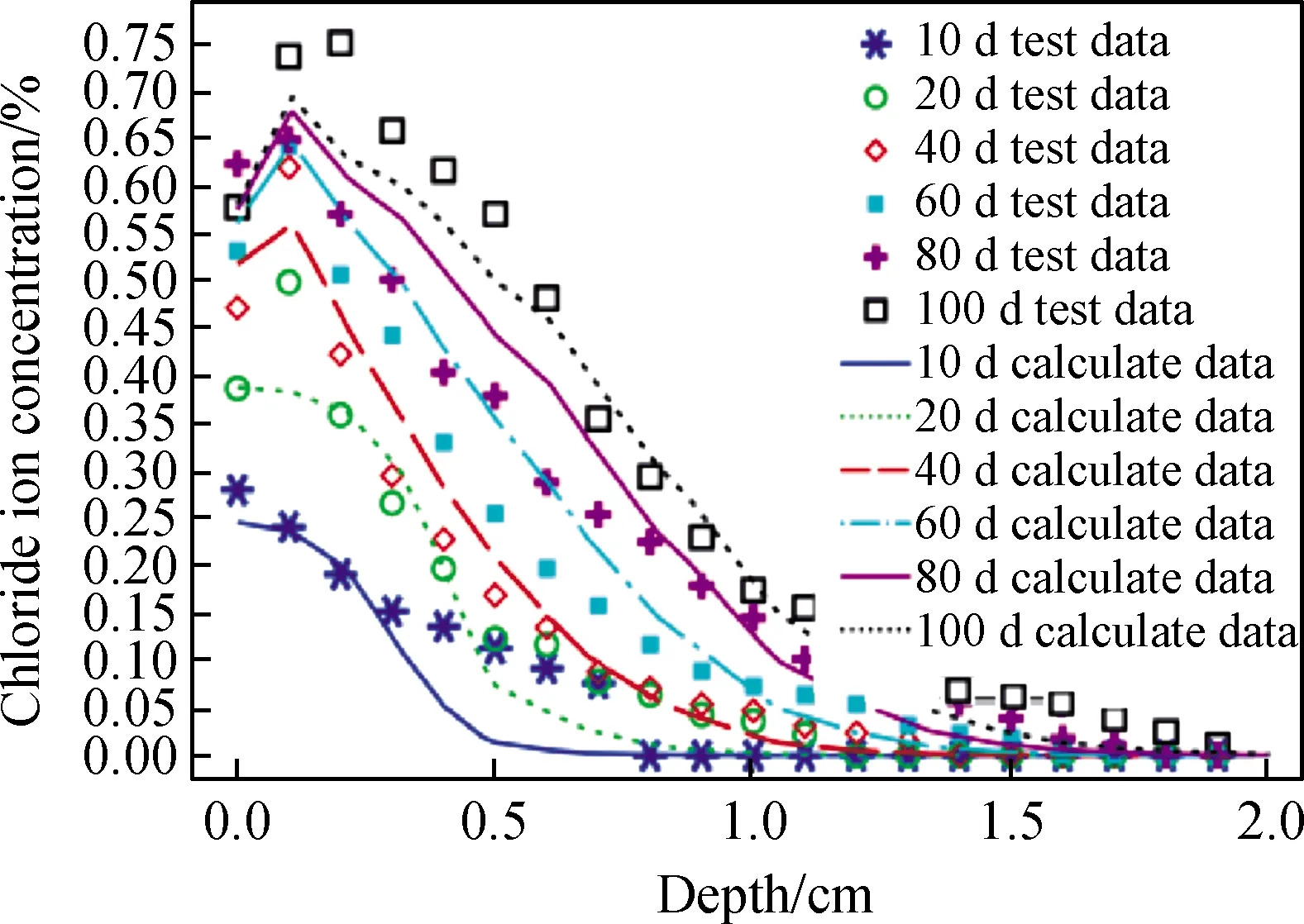
图4 试验结果与模型计算结果比较Fig.4 Comparison between experimental results and model calculation results

借助本文的非饱和混凝土氯离子传输计算模型，采用文献[20]同样的试验条件分别对照分析了10 d、20 d、40 d、60 d、80 d、100 d共6组时变氯离子分布计算结果，与试验结果具体对比情况如图4所示。图中数据显示，无论是氯离子的浅层分布特征、积聚速度，还是整个区域范围内的氯离子分布情况，除了时间周期较短的10 d、20 d两组数据的表层氯离子峰值浓度数据有一定偏差外(上述偏差由于文献[20]的混凝土试件内部初始饱和度无法确定，同时数值模型难以体现混凝土水分扩散系数与氯离子扩散系数在初期的变化复杂所引起)，其他数据都显示了较强的一致性。图中数值计算结果和试验结果均表明，在干湿交替环境下，距离混凝土表面一定深度处都产生了氯离子浓度峰值，且随着时间推移该峰值所对应的深度已基本稳定。计算结果与试验数据较好的一致性表明了随着服役时间的增长，本分析方法及数值模型具有较高的准确性，经第三方试验验证可以足够精确地描述干湿交替环境中氯离子的传输行为，因此可借助此计算分析模型对非饱和混凝土氯离子传输的特性与规律进一步讨论分析。

2 基于非饱和混凝土氯离子传输机理的对流区深度Δx

不同于浸泡环境的混凝土构件，氯离子进入其内部主要是通过扩散方式。处于干湿交替环境中的混凝土，其内部表现为非饱和状态，由对流和扩散的耦合作用推动氯离子的迁移。正是由于对流作用的影响，造成了两种情况中氯离子传输的差异。

2.1 对流区的特点

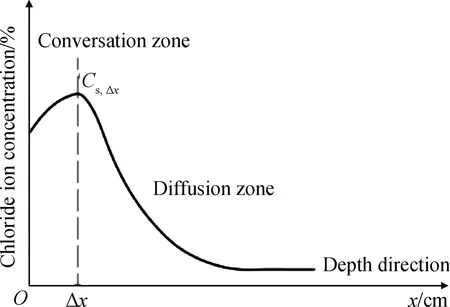
图5 干湿交替条件下混凝土内部氯离子分布情况Fig.5 Distribution of chloride ions in concrete under dry-wet alternation conditions

干湿交替影响下的对流现象作用于混凝土内部，产生了氯离子浓度的局部峰值，以此点为分水岭，并根据驱使氯离子传输的主要作用形式，把混凝土划分为对流区和扩散区二部分。由前述的数值分析及试验结果显示干湿交替条件下混凝土内部氯离子分布情况的抽象曲线，如图5所示。

图5曲线显示，在0≤x<Δx区间内，氯离子传输主要是由对流和扩散耦合作用引起的，曲线逐渐升高至峰值。而在x≥Δx氯离子传输主要由扩散作用引起，曲线呈现扩散方程曲线特性。对流区的存在会对混凝土内部氯离子含量的分布情况和数值大小产生相当的影响，因此分析对流区深度是氯离子传输计算模型的重要内容。

2.2 对流区深度Δx的分析求解方法

在氯离子传输的对流区范围内，描述扩散作用的Fick第二定律已不再适用。但对流区域深度以外的区域，仍可以足够精确地认为氯离子以扩散的形式传输，符合Fick第二定律。因此，可以通过引入对流区深度Δx和其对应的氯离子浓度Cs,Δx这两个参数修正完善Fick第二定律解析解，从而通过简便的计算，预测干湿循环作用下的氯离子分布情况。此模型的重点不是对氯离子的传输规律进行完全的描述，而是对Δx以外区域的氯离子浓度进行较为准确的预测。

国际混凝土联合会(FIB)[8]给出了修正Fick第二定律的简化计算模型，如式(8)所示，可用于计算预测干湿循环作用下混凝土内部氯离子传输。

(8)

式中：Cx,t为混凝土内部氯离子浓度；C0为混凝土内部初始氯离子浓度。

Duracrete[10]结合结构的维修成本总结归纳了Δx的指导经验值，如表2所示。

表2 Duracrete中关于Δx取值规定Table 2 Duracrete requirements on Δx value

根据前述的非饱和混凝土氯离子传输数值计算结果与试验对比分析显示出的对流区规律，本文提出了计算Δx的改进方法。

Δx是经验方法体系的重要参数，但目前有关Δx取值的规定由于缺乏理论支持无法定量，所以一般是通过经验方法确定其值。事实上由于混凝土内部在干湿循环过程中会出现孔隙液蒸发和渗透等复杂过程，其取值主要与结构服役时间、孔隙结构、干燥湿润时间比值、混凝土内部温度场、干燥条件等因素有关。

(1)通过非饱和混凝土氯离子传输数值计算模型可得到干湿交替环境下混凝土内部氯离子含量的最大值和对应的影响深度，该深度即为对流区深度Δx的数值。

(2)将影响深度部分扣除，剩余部分即构成了修正的氯离子分布曲线。

(3)以相应的氯离子浓度值Cs,Δx作为边界条件引入饱水混凝土扩散分析模型中，即可得到基于Fick定律的氯离子分布曲线。

2.3 基于非饱和混凝土氯离子传输机理的对流区深度计算方法验证

为了验证本文所提出的Δx改进计算方法的有效性，同时采用非饱和混凝土氯离子传输数值计算模型和基于Fick定律的饱水混凝土扩散分析模型进行计算，分析对比相应的计算结果。

图6 非饱和混凝土氯离子传输模型计算结果Fig.6 Calculation results of chloride ion transport model for unsaturated concrete

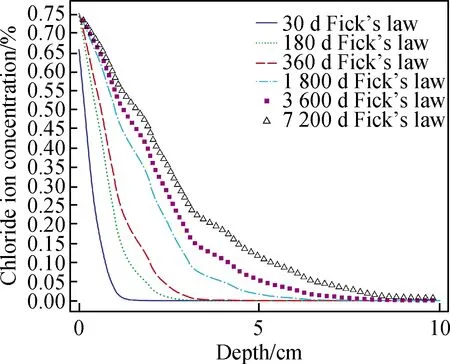
图7 饱水混凝土扩散分析模型计算结果Fig.7 Calculation results of diffusion analysis model for saturated concrete

为了验证修正氯离子扩散曲线与饱水混凝土扩散分析模型求解的氯离子分布曲线的一致性。将对流区Δx深度处对应的氯离子浓度值Cs,Δx作为边界条件引入饱水模型中，采用上述6组试验时长，基于Fick定律进行常规扩散方程求解，将各组计算结果与修正氯离子分布曲线分别进行对比，如图8所示。可以发现在混凝土服役的各个时期，二者都具有良好的相似性和规律的一致性，更好地验证了本文提出计算Δx改进方法的可行性。说明只要能够得到对流区深度Δx，就可以借助扩散方程公式(8)将干湿循环作用下混凝土内部氯离子传输问题简化为常规的氯离子扩散方程的求解，从而将对流扩散耦合问题简化为常规的扩散问题。因此，简化问题的核心就在于确定对流区深度。

图8 基于Fick定律的氯离子分布曲线和修正氯离子分布曲线对比结果Fig.8 Comparison results of chloride ion distribution curves based on Fick’s law and modified model

3 对流区深度的确定及影响参数分析

对流区的形成是氯离子对流扩散耦合作用的结果，其深度必然受到外界多个因素的影响。根据前述分析和沿海结构实际使用特性，本文筛选了服役时间、日平均气温和干燥湿润时间比等参数，分析讨论对流扩散区深度Δx值的变化规律,提出了假定对流区深度拟合公式：

Δx=ηT·ηφ·Δx0

(9)

式中：Δx0为对流区深度基准值；ηT为温度修正参数；ηφ为干湿时间比修正参数。

3.1 服役时间影响

本文在研究服役时间对Δx的影响时，首先考虑单次循环时长分别为2 d、3 d和4 d时，保持其他计算参数不变的情况下取干燥湿润时间比φ=1.0，计算得到服役20年后混凝土结构内部氯离子分布状况，如图9所示。观察发现2 d、3 d和4 d不同条件下的计算结果差异很小，故可认为单次循环时长这个参数对于氯离子传输过程的影响不显著。因此，在后续研究中可以忽略该参数变化所带来的影响。

(10)

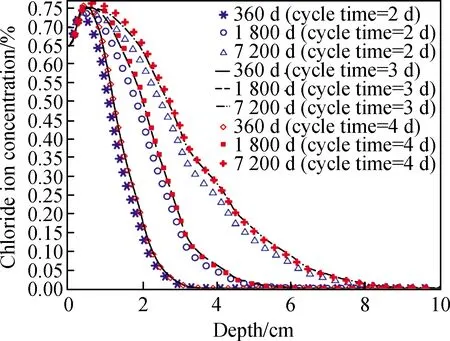
图9 不同单次循环时间计算结果Fig.9 Calculation results of different single cycle time

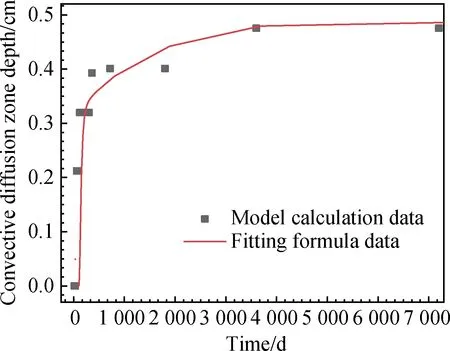
图10 Δx关于时间的拟合结果Fig.10 Fitting results of Δx for time

3.2 温度场影响

为了研究温度场对对流区深度的影响，本文计算了Tav分别为285.15 K、295.15 K、305.15 K和Tam分别为5 K和10 K时这6种温度条件下服役300 d后混凝土内部氯离子分布的状况，如图11所示。分析结果表明气温日变化幅值Tam这个参数对于整个氯离子侵蚀过程的影响并不显著，在后面的计算研究过程中将不考虑该因素的变化。

干燥湿润时间比φ=1.0不变的情况下，在计算中统一选取温度变化幅值Tam=10 K，仅考虑日平均气温的变化，温度计算工况见表3。

分别计算上述各温度工况下6组不同使用时长(分别为30 d、180 d、360 d、1 800 d、3 600 d、7 200 d)对应的不同服役期对流区深度，整理上述6个工况的计算结果，同时以Δx0为基准，拟合得到以日平均气温Tav和服役时间t为自变量的温度修正参数ηT公式，拟合情况如图12所示，拟合优度R2=0.85，拟合效果满足工程需求。

(11)

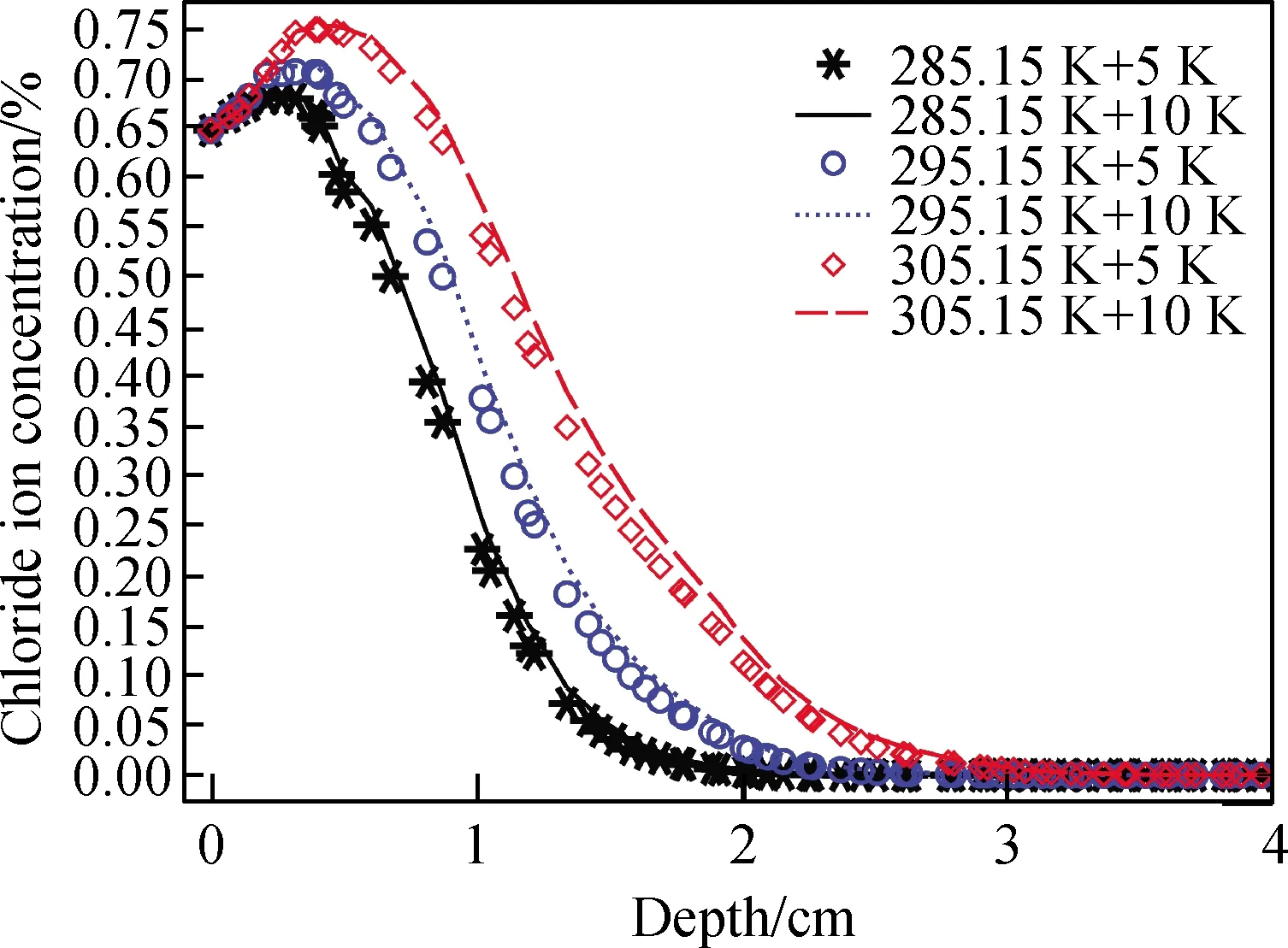
图11 不同温度条件计算结果Fig.11 Calculation results under different temperature conditions

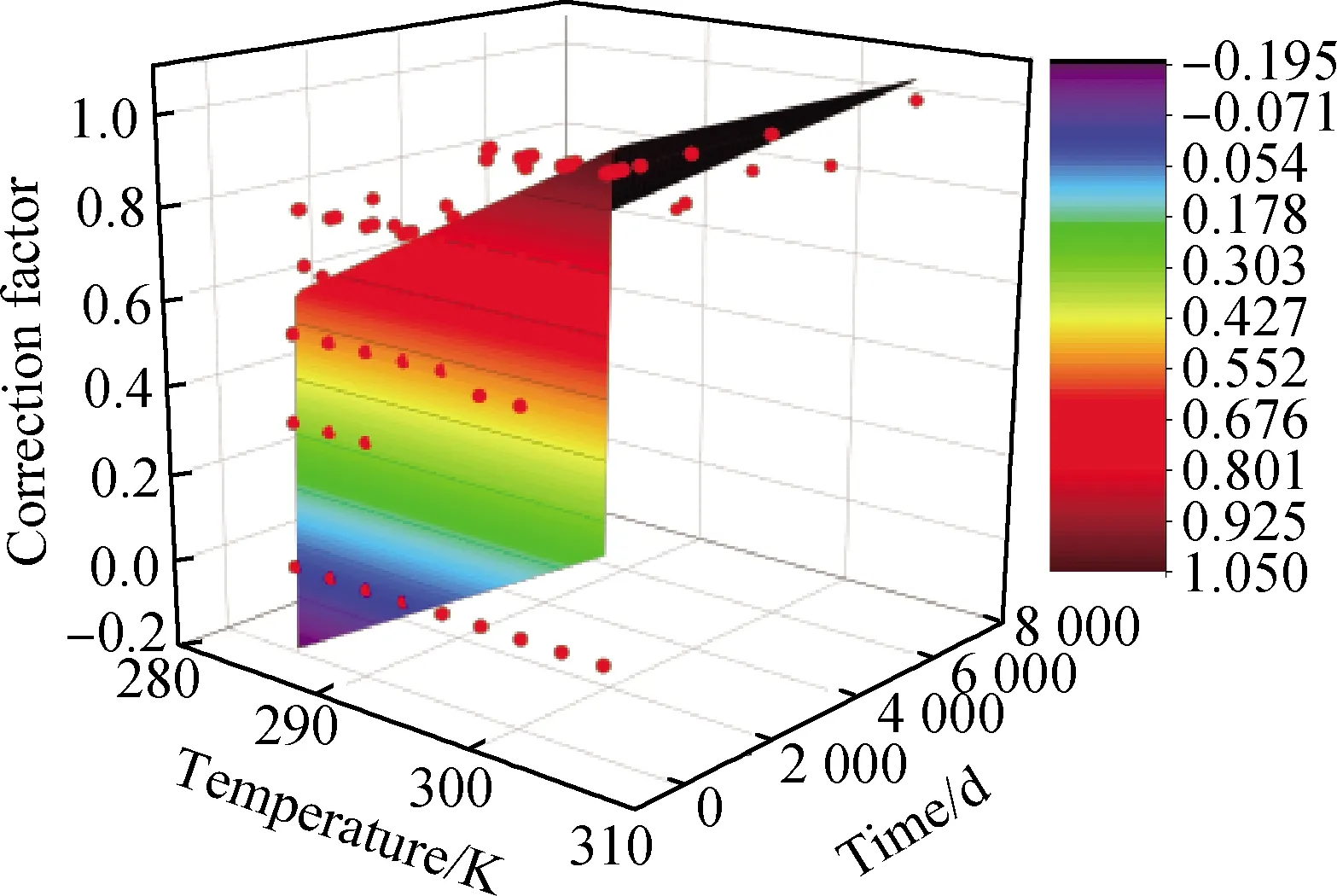
图12 温度修正参数拟合情况Fig.12 Fitting of temperature correction parameters

3.3 干燥湿润时间比影响

(12)

综上所述，将公式(10)～(12)代入公式(9)中即可确定对流区深度的预测值。该计算模型主要考虑了服役时间、日平均气温和干燥湿润时间比等参数，将单次循环时长和气温日变化幅值这两个影响较小的参数剔除。

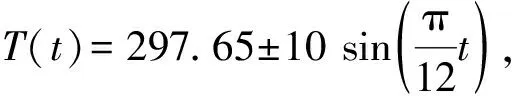
图13 干湿时间比修正参数拟合情况Fig.13 Fitting of modified parameters of dry-wet time ratio

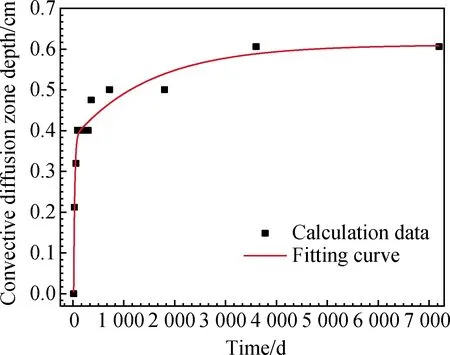
图14 校核计算结果Fig.14 Checking calculation results

4 结 论

针对干湿交替环境下混凝土内部的氯离子传输受到对流与扩散耦合作用，本文给出了非饱和混凝土内部氯离子传输计算模型和分析方法，该方法可以方便地将对流与扩散耦合问题解耦为含有对流区深度Δx的常规扩散方程，并进一步给出了对流区深度Δx的拟合公式，为准确预测干湿交替环境中的氯离子传输规律、简化计算模型提供了解决的思路和方法，具体的研究结论如下：

(1)以混凝土细观尺度分析模型为基础，引入环境温度场变化、水分迁移和氯离子传输等因素建立了干湿交替区域氯离子传输数值计算模型，通过试验数据对表层氯离子分布特征、累积峰值深度及混凝土全区域氯离子分布规律的分析对比，证实本计算模型的准确性和有效性，说明该类综合了温度场、水分迁移与氯离子传输的混凝土细观数值模型可以精确地描述干湿交替环境下混凝土内部氯离子的传输机制和行为。

(2)通过对干湿交替环境下混凝土内部氯离子的运移机制与传输行为的分析，证明了对流区深度Δx的存在，并有效地将氯离子扩散曲线整体解耦为对流区部分及其后的扩散区部分，为此类问题的简化提供了求解思路。

(3)针对流区深度Δx，剔除低影响因子后，以计算服役时间、日平均气温和干湿时间比为主要影响因子给出了对流区深度Δx拟合公式Δx=ηT·ηφ·Δx0，并验证了该公式的适用性及准确性。

上述结论可为处于干湿交替环境中的混凝土结构氯离子传输问题的计算提供简化而较为准确的方法，为沿海混凝土结构内部氯离子的传输作用机理和分布状态研究提供参考。但是，本文的研究内容对环境温度场的变化考虑较为简化，未引入大体积混凝土内部温度梯度的影响；同时尚未验证在自然降雨环境中模型的适用性，后续将通过深入了解环境条件变化情况进一步展开研究。