基于UDEC-GBM的矿物晶粒解理特征对硬岩石破坏过程的影响

胡小川，丁学正，苏国韶，廖满平

1) 中建二局土木工程集团有限公司，北京 101100 2) 广西大学土木建筑工程学院，南宁 530004 3) 广西大学工程防灾与结构安全教育部重点实验室，南宁 530004

硬质岩石失稳过程及其机理研究是岩石力学与工程科学的重要研究内容[1].近几十年来，岩石力学科学得到了迅猛的发展，理论、试验及数值仿真成为研究、认识岩石破坏过程的有力工具.目前为止，基于室内物理试验，硬质岩石微观破裂过程方面的研究取得了丰富的成果，并认为其过程一般存在以下几个关键特征[2-5]：(1) 裂纹闭合，该阶段主要来源于原生孔隙、孔洞及微裂纹的闭合；(2) 新裂纹的产生，该阶段一般发生在0.3～0.5倍单轴抗压强度（UCS），其对应的起裂应力σci一般作为现场岩体强度的下限[6]，具体和岩石类型及其微观矿物构造有关，并伴有声发射（AE）信号出现；(3) 裂纹的孕育，此时微裂纹之间还没有相互作用，其裂纹级别一般限制在晶粒级别，分布一般较为分散[7]；(4) 裂纹的联合贯通，此时微裂纹密度已增加数倍，晶粒级别的裂纹开始相互作用、联合及贯穿，形成尺度较大的宏观破裂，也常伴随剪切破裂事件的发生及AE信号快速增加，该阶段一般发生在0.7～0.8倍UCS，其对应的损伤应力σcd常作为现场岩体的长期强度或岩体强度的上限值[6].

然而，岩石材料本身具有非均值性，受载过程中的响应非常复杂，这些关键特征也不断发生变化，具体受岩石内部矿物颗粒微观结构、尺寸及分布影响，即使是取自同一块完整岩石的试件所具有的力学性质及相同加载条件下的响应也不尽相同.事实上，即使相同比例的岩石，其矿物的排列、组合不同也会导致岩石的性质存在一定的差异，而数值仿真作为有效探究微观开裂机制的手段之一，在探究颗粒尺寸、结构对岩石响应时具有明显的优势，因而得到了广泛应用.目前为止，考虑颗粒级别的岩石力学性质、开裂过程相关方面已有大量研究.例如，蒋明镜等[8]对铝棒胶结模型和BPM（Bonded-particle model）模型进行了对比，认为基于颗粒的铝棒胶结模型同样能有效模拟岩石真实响应；Peng等[9]调查了晶粒尺寸非均匀性对岩石开裂过程、力学性质及微观机理的影响；Gao等[10]调查了晶粒级别的三角形块体在室内岩石力学方面的应用.然而，晶粒方面涉及太多复杂因素，晶粒几何结构、晶粒尺寸分布等方面的研究仍然不足，基于晶粒级别开展岩石开裂过程及机理方面的研究仍然非常重要.

实际上，很多显晶硬质岩石的微观开裂过程都涉及沿晶破坏、晶内破坏及穿晶破坏[11-15].那么，矿物晶粒的本质属性势必影响岩石微观开裂过程，进而影响岩石的宏观响应，考虑晶粒本质属性成为调查硬质岩石微观破坏需要考虑的重要因子.事实上，晶粒具有极完全解理、完全解理、中等解理、不完全解理和极不完全解理（无解理）等方面的特质.解理是指矿物晶体在外力作用下严格沿着一定结晶方向破裂而能产生的光滑平面.例如，微观观察发现，长石具有不同方向、不同间距及不同类型的解理[11].因此，在相同荷载大小、方向条件下，岩石可能会因为其内部矿物颗粒解理而表现出不同的力学响应.因此，基于颗粒级别的穿晶破坏方面的研究，学者们也取得了众多的进展.例如，Potyondy[7]基于PFC2D提出通过平滑节理接触和平行接触模拟可破坏的矿物晶粒，这样首次实现了晶粒的穿晶破坏模拟；Abdelaziz等[16]采用基于颗粒的有限元和离散元结合方法（FDEM）模拟了岩石颗粒级别的穿晶、沿晶破坏，成功捕捉了岩石的微观及宏观响应；Wang和Cai[13]采用Neper建模技术在3DEC中实现了穿晶破坏的模拟，详细地介绍了穿晶接触非均值性对岩石压缩、拉伸性质及开裂过程的影响.通过以上调查发现，穿晶模拟更为有效地模拟了岩石矿物晶粒可破裂的特质，然而大部分研究均还停留在通过设置不同的晶体内及晶体间接触（离散元中颗粒或块体之间接触部分称为“接触”）参数进而在数值加载中实现穿晶、沿晶的模拟，但均未对晶粒解理属性（例如解理倾角、间距）对岩石的力学性质及微观开裂机制做更多研究.

本文采用离散单元法模拟岩石在颗粒级别的穿晶破坏，研究矿物晶粒内部解理倾角、间距及解理围压效应对岩石微观力学性质及微观开裂机制的影响，为进一步从晶粒级别认识显晶质岩石复杂的力学性质、破坏过程提供参考和借鉴.

1 试件描述

本试验选取自广西梧州市岑溪县红色中粗晶粒花岗岩作为试验对象，该花岗岩弹模约32.2 GPa，单轴压缩强度UCS约115.4 MPa，其峰前应力-应变呈明显线弹性关系，属于典型的硬、脆性岩石.宏观观察、偏振光观察显示该花岗岩属于典型的显晶质结构，见图1，且该类花岗岩主要由多边形矿物颗粒镶嵌、内锁组成，矿物晶粒直径在2～22 mm之间分布，按粗粒（晶粒直径>5 mm）、中粒（5 mm≥晶粒直径>2 mm）、细粒（晶粒直径≤2 mm）的晶粒尺寸划分标准，属于细中晶粒花岗岩.矿物成分分析显示，该类花岗岩主要由10%斜长石、27%石英、58%钾长石、3%黑云母及2%其他组成（均为体积分数）.电子显微镜（SEM）观察显示，岩石内部存在一些原生裂隙、孔洞，这有助于认识硬、脆性岩石张性破坏的产生和孕育.花岗岩基本物理、力学参数见表1.

图1 岩石材料Fig.1 Rock material

表1 基本物理与力学参数Table 1 Basic physical and mechanical parameters

2 模型配置

本文采用UDEC商业软件进行模拟[17]，因为基于颗粒的UDEC方法（UDEC-GBM）所建立模型（完全接触、内嵌）内部矿物颗粒之间全接触的形式更能有效地、真实地反映岩石的泊松比、拉压比例及矿物颗粒之间内锁问题[18].从真实矿物几何结构上讲，相对于UDEC中的三角形块体及PFC2D中的圆盘颗粒，多边形颗粒更能现实地模拟岩石内部的矿物颗粒，反映矿物颗粒的微观结构特征.例如，图1显示矿物晶粒总是以非规则的多边形镶嵌.从数值模拟效果上看，多边形块体使岩石更易出现张拉破坏，破坏边缘较为不规则，而三角形块体通常使得岩石更加倾向于剪切开裂，破坏路径相对光滑，见图2，其中v表示加载速度.考虑到岩石矿物颗粒真实结构和硬质岩石单轴下更倾向于张拉破坏现象，本文采用UDEC中泰森多边形（Voronoi）对岩石进行离散.但是，本文仅仅模拟岩石的平均颗粒尺寸和不同比例的矿物成分，并不追求实现真实的矿物颗粒尺寸分布，因为这在UDEC建模中还存在一定的困难.同时，目前的模型也并不追求实现同真实矿物颗粒的几何结构完全相同，因此用泰森多边形代替矿物颗粒是对矿物颗粒的几何结构进行一定简化的结果.

图2 Voronoi模型和Trigon模型破坏路径比较Fig.2 Comparison of potential failure paths between the Voronoi model and Trigon model

本文采用Gao等[19]提出的模拟穿晶破坏的方法进行模型设置：(1) 按照真实矿物颗粒的平均尺寸（4.5 mm）用泰森多边形对岩石进行离散；(2) 按照岩石真实矿物比例（见表2）对多边形进行分类，多边形之间形成的接触定义为沿晶接触；(3) 通过连接多边形颗粒的中心和角点对多边形进行进一步离散，内部新产生的接触定义为晶内接触，为穿晶破坏提供了可能的路径.通过赋予沿晶接触和晶内接触不同的力学性质就可以实现岩石材料的沿晶及穿晶破坏的模拟.图3给出了含有4类矿物成分的数值试件（未考虑原生裂隙和孔洞；其中，①代表钾长石穿晶开裂，②代表黑云母沿晶开裂），并给出了穿晶、沿晶模拟结果，其微观开裂结果和真实开裂一致，矿物具体成分和参数见表2.同时，选择库伦滑移模型作为接触的本构模型.当接触上的剪力或者张力超过对应的强度极限时，接触会产生相应的剪切或张拉破坏，块体采用弹性模型，图4详细描述了接触本构关系，其在线弹性阶段的法向和切向应力-位移之间的关系为[17]：

表2 矿物晶粒物理、力学参数Table 2 Physical and mechanical parameters of grains

图3 模型配置Fig.3 Model configuration

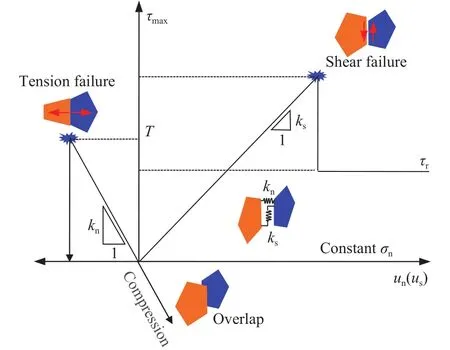
图4 本构关系Fig.4 Constitutive relationship

式中，kn、ks、Δσn、Δτs、Δun和分别为法向刚度、切向刚度、法向应力增量、切向应力增量、法向位移增量和切向位移增量.当接触的法向应力 σn超过其抗拉极限T时，法向应力 σn则减小为0；当接触的剪应力达到其对应抗剪强度τmax=cp+tanφp时，接触剪应力修正为： τr=cr+tanφr；cr和cp分别代表接触的残余粘聚力及其峰值； φr和φp分别代表残余摩擦角及其峰值； τmax和τr分别代表峰值剪应力和残余剪应力.

此外，离散单元法中的参数和物理世界的参数有一定差距，需要通过数值试验反复校核，以达到模拟真实岩石宏观响应（弹性模量、泊松比、单轴或多轴强度及起裂应力等）的目的.本文参考前面描述的花岗岩试件的单轴试验结果进行大量的微观参数校核，其校核后的参数和结果见表2～5，数值和物理单轴应力-应变曲线见图5.可见，数值得到的宏观力学、强度参数同物理试验结果基本一致.就应力-应变曲线而言，数值和物理试验的结果具有一定的差异，前者并没有加载前期的压缩阶段，直接呈现线弹性特征，这已在众多研究成果中被发现[20-21].以上差异是由于本文未考虑岩石的原生裂隙、孔洞，且块体被赋予线弹性本构.应力-应变曲线其余阶段均类似.图6为数值模拟和室内试验的破坏结果，宏观、微观裂纹都揭示了数值模拟同物理试验的破坏结果一致.综上，认为校核的参数和模型可进一步用于该类岩石的相关数值试验.

表3 加载钢板参数Table 3 Properties of the loading platens

表4 接触微观参数Table 4 Microparameter of contacts

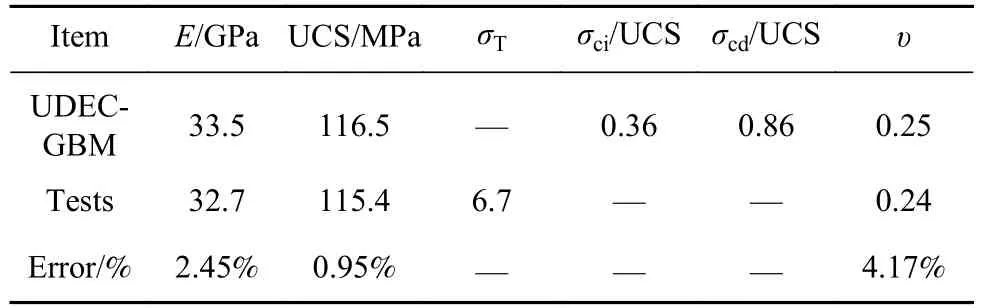
表5 参数校核结果Table 5 Calibrated results of properties

图5 应力-应变曲线对比Fig.5 Comparison of stress-strain curves

图6 破坏结果.（a）数值试件；（b）微观裂纹；（c）物理试验Fig.6 Failure results: (a) numerical specimen; (b) microcracks; (c)physical test

3 数值试验

3.1 解理倾角的影响

本文设置 0°、20°、40°、60°及 90°五类不同解理倾角，以调查矿物颗粒内部解理倾角对岩石力学响应及微观开裂过程的影响.倾角方向以水平向为0°.不同解理倾角可通过UDEC中节理单元在需要离散的矿物颗粒内部生成.长石（本文特指钾长石）矿物晶粒具有典型的解理特征，因此本文以长石晶粒为例，对长石晶粒用节理单元按照不同倾角进行离散，其余矿物颗粒仍采用Gao等[19]提出的模拟穿晶的方法进行离散.图7给出了长石节理倾角为0°下的数值模型及解理倾角为0°和20°的局部放大模型.解理之间的间距均设置为2 mm，其他解理倾角下模型内部颗粒大小、分布完全相同，仅解理倾角不同，这样建立的解理模型同真实解理不仅具有较好的类似性，而且不同解理倾角的模型间可以相互比较，以调查倾角的影响.此外，本文采用竖向位移控制方式进行加载（该部分为单轴加载），加载速率为0.1 m·s-1，对应约每步10-7m，满足准静破坏要求和UDEC的基本假设（一个时间步内的响应只能传递到相邻的块体），且不同倾角下的模型运行相同步数，以便对比解理倾角的影响.注意，数值的速度是数学意义上的速度，是用来满足数值稳定性的，同真实物理世界的速度有很大区别.

图7 数值模型.（a）数值试件；（b）内部矿物晶粒；（c）解理倾角和间距定义Fig.7 Numerical model: (a) numerical specimen; (b) mineral grains; (c)definition of cleavage angle and spacing

图8为不同解理倾角下的单轴应力应变曲线.可见，解理倾角的变化对岩石峰前及峰后响应都有一定的影响.峰前，弹性模量先由倾角为0°时的34 GPa下降至倾角为20°时的33.5 GPa，随后弹性模量呈现单调增加趋势，见图9；峰后，0°时岩石峰后延性特征相对明显，而随着钾长石解理倾角的增加，岩石的峰后脆性更为明显.此外，单轴强度随倾角的变化相对复杂，在倾角为40°和60°时下降到了最低值，随后强度随倾角的增加而增加，见图9.弹性模量和强度的变化同梁等[22]对具有不同层理方向的砂岩进行了单轴试验所展示的试验结果一致.虽然本文仅进行单一矿物颗粒解理倾角的变化，同宏观具有不同层理方向岩石试件有所区别，但试验结果仍具有类似性，说明本次数值试验的合理性.

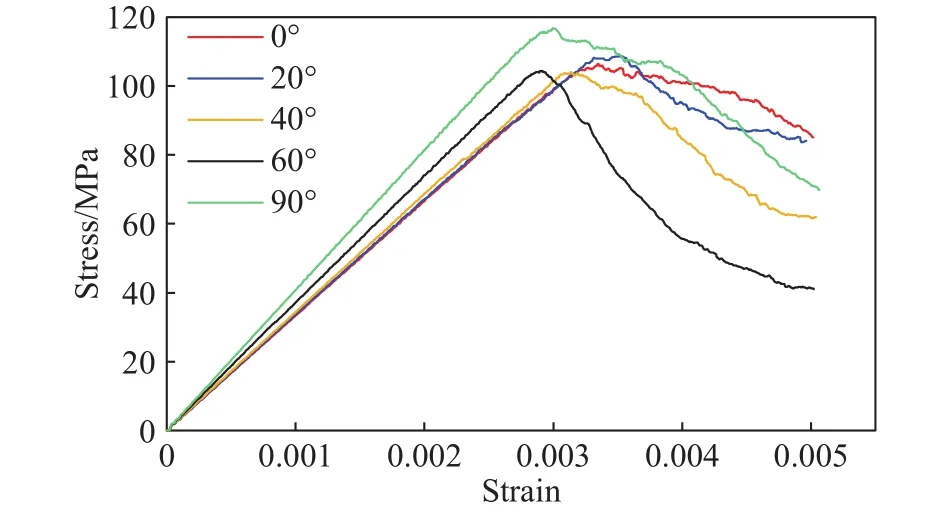
图8 不同解理倾角下单轴应力-应变曲线Fig.8 Uniaxial stress-strain curves at different cleavage angles

图9 单轴抗压强度和弹性模量Fig.9 Uniaxial compressive strength and elastic modulus

为监测解理倾角对微裂纹孕育的影响，对裂纹的孕育过程进行了监测，并以90°解理倾角下岩石内部微裂纹演化过程（图10）为例进行简要介绍.可见，张拉裂纹在应变为0.125%的时候开始产生，剪切裂纹0.264%开始产生，与传统对岩石的基本理解（先张拉后剪切）一致[4,18].同时，穿晶裂纹基本都在应变为0.328%时产生，靠近峰值或峰后，且数量上远小于总体裂纹数量，说明总体上仍是以沿晶张拉、剪切破坏为主.

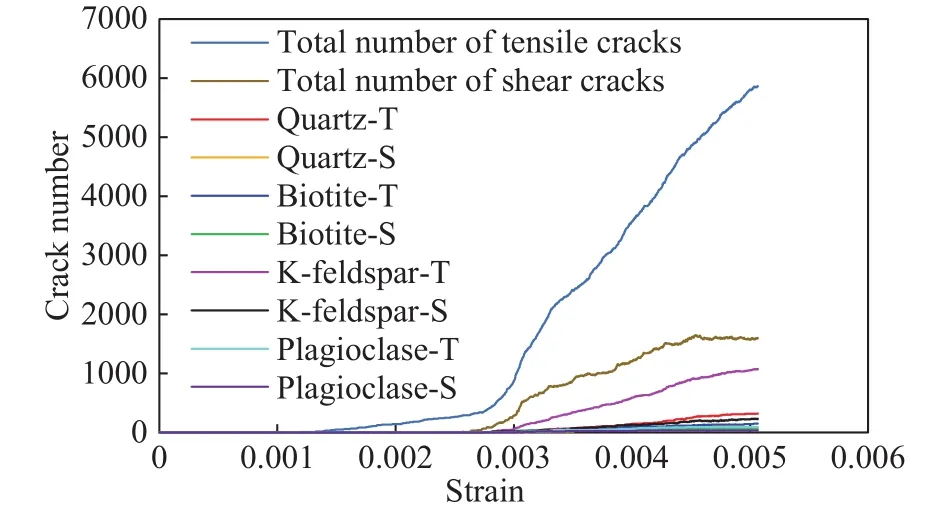
图10 90°解理倾角下总裂纹演化过程（T和S分别代表张拉和剪切开裂）Fig.10 Evolution of the total crack at the 90° cleavage angle (T and S indicate tensile cracking and S cracking, respectively)

图11为总穿晶、沿晶裂纹数与解理倾角的关系.可以发现，随着解理倾角的增加，穿晶裂纹的数量单调增加，而沿晶裂纹数量在倾角为60°时降至最低值，然后上升；同时，沿晶裂纹受解理倾角影响较大，随倾角增加单调减少，其与穿晶裂纹的比值由11.1下降到2.6，且倾角为60°以后下降缓慢，见图12.图12还显示总张拉裂和总剪切裂纹的比例也受解理倾角的影响，比例在40°～60°时达到最大值.因此，解理倾角不仅影响晶粒内部自身的微观机制，还会影响晶粒之间的微观开裂机制，从晶粒间和晶粒内两个方面共同影响岩石的宏观响应.

图11 穿晶裂纹和沿晶裂纹数量Fig.11 Number of trans- and intergranular cracks

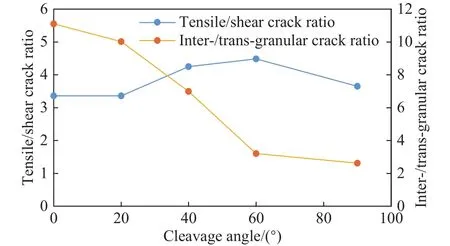
图12 微裂纹比例与解理倾角关系Fig.12 Relationship between the crack ratio and cleavage angle

图13为不同解理倾角下穿晶裂纹的数目，可见钾长石矿物晶粒内部解理倾角变化对微观破坏机制影响显著.钾长石穿晶张拉、剪切随解理倾角变化而变化，且石英张拉机制也受到了影响，最开始以石英张拉破坏为主导，因为石英含量最多，且这个机制在解理倾角≤40°时一直成立；当解理倾角>40°时，微观破坏机制发生变化，钾长石穿晶（穿晶张拉>穿晶剪切）破坏成为了主导的微观机制.

图13 不同类型穿晶裂纹数量（T和S分别代表张拉和剪切开裂）Fig.13 Number of different transgranular cracks (T and S indicate tensile cracking and S cracking, respectively)

图14为不同解理倾角下的试件的宏观破坏模式，尽管微观破坏过程受矿物颗粒内部解理倾角的影响，但宏观破坏模式却几乎不受影响，都是以宏观劈裂主导，这同单轴试验中总是观察到的以劈裂为主的现象较为一致，说明单轴条件下，就钾长石晶粒解理倾角而言，其变化并不影响岩石的宏观破坏模式.

图14 不同解理倾角下宏观破坏.（a）0°；（b）20°；（c）40°；（d）60°；（e）90°；（f）单轴压缩试验结果Fig.14 Macroscopic failure at different cleavage angles: (a) 0°; (b) 20°; (c) 40°; (d) 60°; (e) 90°; (f) test result under uniaxial compression

3.2 围压对矿物颗粒解理倾角效应的影响

围压对岩石变形、强度特征及开裂机制都有较为明显的影响[23-25].因此，该部分数值试验以3 MPa围压为例，在解理倾角为20°及间距为2 mm的条件下展开围压对解理倾角效应影响研究.图15为常规三轴加载应力-应变曲线，与单轴相比，峰后存在围压效应，岩石的延性增加明显.三轴下岩石的弹模同单轴下弹模演变规律基本一致，60°、90°下的弹模有少量增加，但总体而言弹模围岩效应相对不明显，见图16.强度变化规律同单轴下差异相对较大，尤其是解理倾角由40°增加到60°时，强度下降明显.图17为3 MPa下不同类型穿晶裂纹数量，同0 MPa下（图13）不同类型穿晶裂纹数量规律基本一致.图18和图19分别为0 MPa及3 MPa时不同类型穿晶裂纹所占总穿晶裂纹的比例，可见解理倾角的围压效应主要体现在3 MPa时20°、40°解理倾角下石英张拉穿晶裂纹比例减少，40°下钾长石张拉穿晶裂纹比值减少和钾长石剪切穿晶裂纹显著增加.此外，围压还会导致沿晶裂纹和穿晶裂纹数量和比值发生变化.图20为3 MPa围压下穿晶裂纹和沿晶裂纹数量，穿晶裂纹总体增加，而沿晶裂纹比0 MPa下的数量相对减少（图11），尤其在60°时，沿晶裂纹减少最为明显.就沿晶和穿晶裂纹比例而言，0 MPa下比值比3 MPa下比例下降更为明显，解理倾角由0°到90°增加过程中，围压为0 MPa时沿晶和穿晶的比值由4.6下降到1，见图12；当围压为3 MPa时，沿晶和穿晶的比值由2.17下降到1.92，见图21.因此，解理倾角≤60°时，3 MPa围压下沿晶裂纹相对减少，而>60°时，围压的增加又导致沿晶裂纹相对增加.总之，晶体解理倾角效应受围压影响.

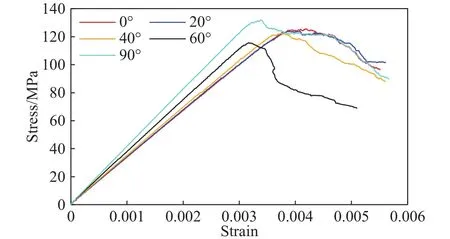
图15 应力-应变曲线（3 MPa）Fig.15 Stress-strain curves at 3 MPa

图16 三轴抗压强度和弹性模量Fig.16 Triaxial compressive strength and elastic modulus

图17 3 MPa时穿晶裂纹数量分布Fig.17 Number of transgranular cracks at 3 MPa

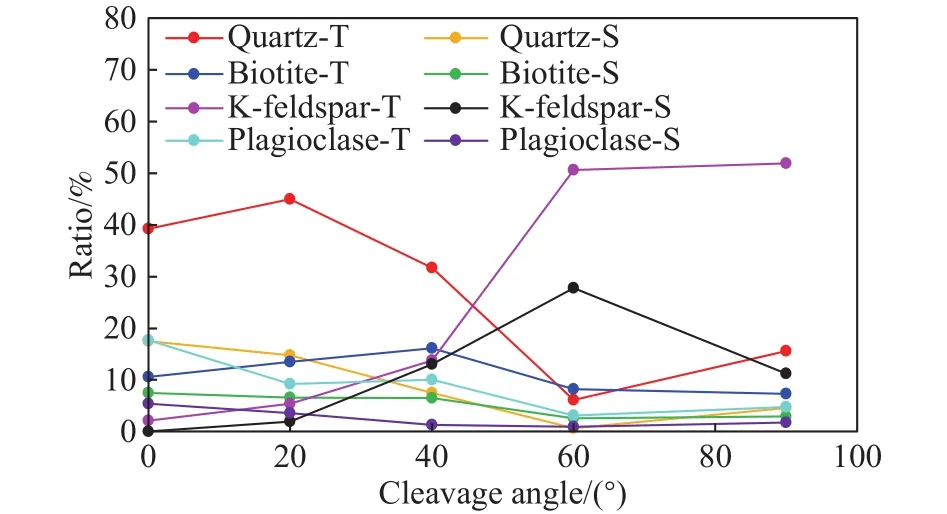
图18 0 MPa时不同类型穿晶裂纹占总穿晶裂纹比例Fig.18 Ratio of different types of transgranular cracks to the total transgranular cracks at 0 MPa

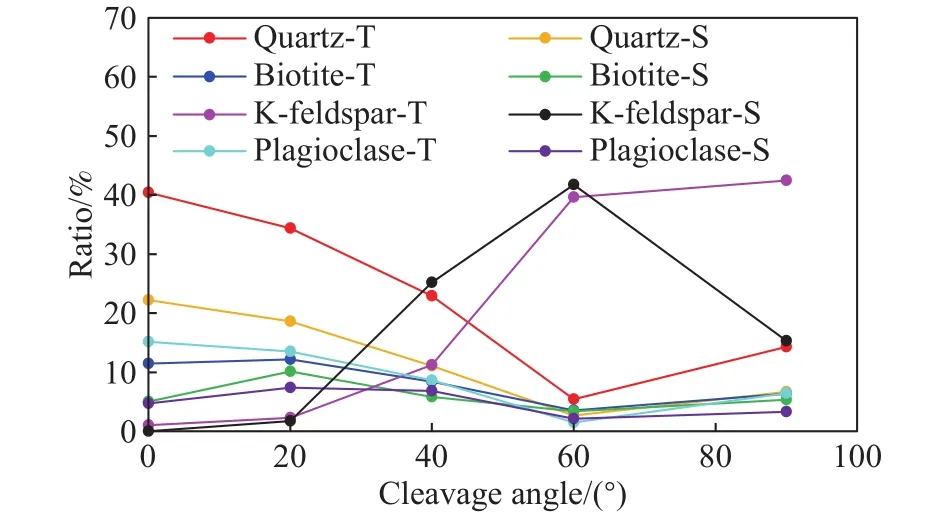
图19 3 MPa时不同类型穿晶裂纹占总穿晶裂纹比例Fig.19 Ratio of different types of transgranular cracks to the total transgranular cracks at 3 MPa

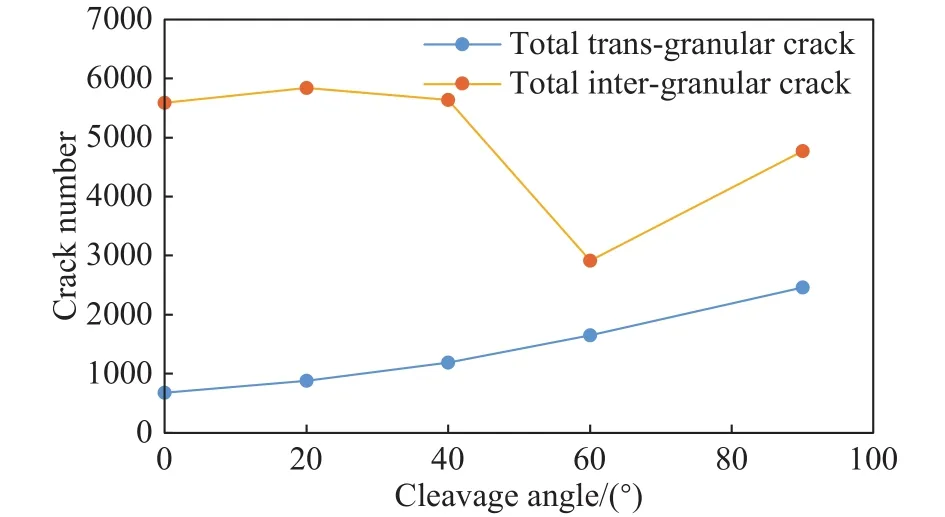
图20 3 MPa时穿晶裂纹和沿晶裂纹数量Fig.20 Number of trans- and intergranular cracks at 3 MPa

图21 3 MPa时微裂纹比例与解理倾角关系Fig.21 Crack ratio at different cleavage angles (3 MPa)

3.3 解理间距的影响

长石晶粒内部解理的间距是变化的，有的解理间距较大，有的间距较小，这取决于岩石本质属性[11].晶粒内解理间距的变化势必会改变裂纹扩展的路径，进而影响岩石在受载过程中的微观破坏机理.因此，有必要调查晶粒内部解理间距对岩石微观破坏机制的影响.解理间距定义见图7（c）.本文采用2、2.5、3和4 mm四种不同解理间距对钾长石晶粒进行离散，并以解理倾角20°为例进行单轴试验，以调查解理间距效应.

图22为不同晶粒解理间距下的单轴应力应变曲线，可见解理间距对峰值强度影响不大，但对弹性模量有一定影响，间距的增加会导致弹性模量的增加.图23、图24和图25为不同类型裂纹在不同晶内解理间距下数目变化.总体而言，穿晶裂裂纹随间距的增加有少量增加（图24），体现在黑云母剪切裂纹和斜长石张拉裂纹数量上（图23），钾长石穿晶张拉、剪切裂纹有少量减少（图23）.但是，晶粒解理间距增加对沿晶裂纹的影响相对较为显著，使得数量不断减少.因此，总的沿晶裂纹和穿晶裂纹的比值不断下降，但当晶粒解理间距≥3 mm后比值几乎保持不变（图25）.图25还显示了总张拉裂纹和剪切裂纹比例随晶粒解理间距的变化.结果显示，虽然裂纹数量受影响，但张拉裂纹和剪切裂纹的比值却基本保持不变，对岩石微观张拉、剪切破坏机理几乎无影响.

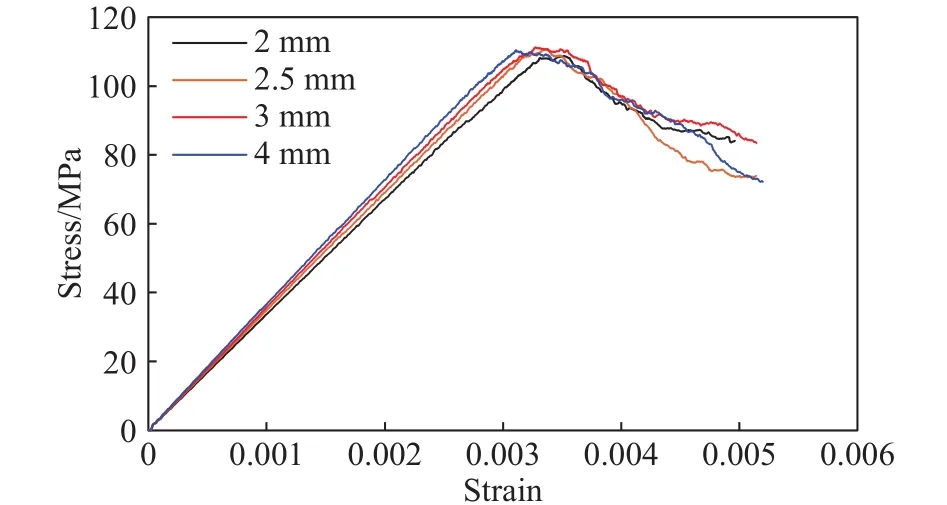
图22 不同解理间距下单轴应力-应变曲线Fig.22 Uniaxial stress-strain curves at different cleavage spacings

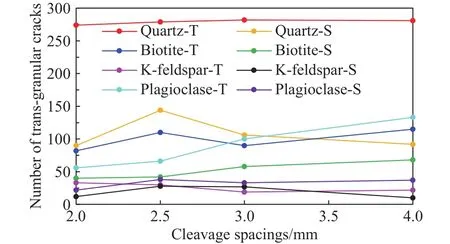
图23 不同解理间距下的穿晶裂纹数量Fig.23 Transgranular cracks at different cleavage spacings

图24 不同解理间距下的裂纹数量Fig.24 Number of cracks at different cleavage spacings

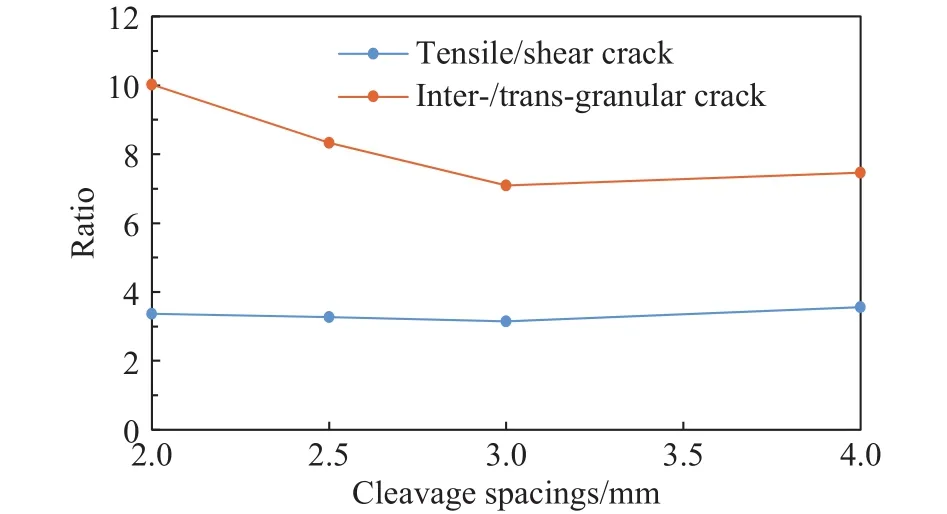
图25 不同解理间距下裂纹比例Fig.25 Crack ratio at different cleavage spacings

4 讨论

本文数值试验表明，岩石开裂受矿物晶粒解理特征影响.图26为岑溪花岗岩在某次加载后偏光显微镜下的开裂破坏.可见，当主开裂和晶粒的解理方向基本一致时，主裂纹表面光滑，裂纹两边岩石相对位错较小，张拉破坏明显；当主开裂和晶粒解理方向有一定倾角时，破坏相对复杂，主开裂在孕育过程中出现了分叉，且其附近有岩石被剪成小块的现象，伴有剪切破坏.因此，微观层面的观察再一次证实了硬质岩石开裂破坏受矿物晶粒解理特征影响.

图26 解理对开裂的影响Fig.26 Influence of cleavage on cracking

实际，矿物晶粒的解理特征也会对岩石的宏观破坏产生影响，例如深部破坏中的板裂和岩爆现象.岩爆烈度与岩石的强度、峰后属性等因素有关[5,26]，而本文研究显示解理倾角对岩石强度、峰后的脆延特征等有明显的影响.图8和图15的应力-应变曲线表明，60°解理倾角下岩石强度较低，峰后刚度或局部刚度较大，易发生剧烈或局部剧烈的破坏，例如岩爆.因此，晶粒内部纹理特征对岩爆烈度也会造成影响，特别是在含有解理的矿物颗粒含量较大，且颗粒本身性质对岩石性质响应影响也显著的条件下，晶粒内部的纹理特征更是不容忽视.随着数值模拟技术的发展，穿晶裂纹的模拟得到了实现，而为更加真实地模拟矿物颗粒对岩石性质、响应的影响，晶粒解理特征更是不容忽视.本文则正是基于这一点，通过对不同晶粒内部解理方向、间距下岩石性质和开裂机理展开调查，完善了晶粒级别微观各向异性对硬质岩石性质、响应的影响方面的研究.

此外，本文基于晶粒解理特征的数值调查还存在以下不足：(1) 矿物颗粒真实的解理间距更小，但由于目前计算能力的限制，仅调查了2、2.5、3 和4 mm四种较大解理间距下的解理特征对硬质岩石微观破坏过程的影响，同真实矿物晶粒内部解理结构或分布还存在差距；(2) 本文仅是基于钾长石调查晶粒解理效应，其他矿物晶粒的解理效应在后续研究中也应给与考虑；(3) 本文基于平均颗粒尺寸和矿物成分比例进行模型的建立，并未按真实矿物颗粒尺寸分布建立模型，后续的数值试验应考虑颗粒的真实尺寸分布.

5 结论

本文基于离散单元法软件UDEC，从晶粒级别出发，详细研究了解理倾角、解理倾角围压效应及解理间距对硬质岩石力的学性质、微观开裂过程及机理方面的影响，并探讨了晶粒解理特征在工程实际中可能带来的影响.数值模拟研究结果表明：

（1）晶粒解理具有明显的倾角效应.当钾长石晶粒的解理倾角由0°增至90°时，岩石的弹性模量、单轴压缩强度、峰后脆延特征都会发生变化.同时，整个开裂过程仍由张拉沿晶主导，但穿晶裂纹数量随解理倾角增加不断增加，而沿晶裂纹数量呈现减少趋势.穿晶裂纹数量受解理倾角影响大，主要体现在随着倾角增加，钾长石张拉穿晶裂纹显著增加，钾长石剪切裂纹数量在60°增加到最大值后减少，石英穿晶张拉裂纹数量也有明显变化，而其他穿晶裂纹数量基本无明显变化.

（2）晶粒解理倾角效应受围压影响.20°、40°解理倾角下的石英张拉穿晶比例减少，40°下钾长石张拉穿晶裂纹减少和钾长石剪切穿晶裂纹显著增加.同时，围压还会导致沿晶裂纹和穿晶裂纹数量和二者比例发生变化，但取决于具体的倾角，不同倾角下围压对沿晶裂纹和穿晶裂纹数量和比例变化影响不一样.

（3）晶粒解理间距对岩石微观开裂过程有影响.随着钾长石晶粒解理间距由2 mm增加到4 mm，穿晶裂纹中除石英张拉外，其余穿晶裂纹数量均有一定的变化，穿晶裂纹总体有增加趋势，而沿晶裂纹数量总体减少.随着解理间距的增加，各类型裂纹数量发生变化，但总的剪切裂纹和张拉裂纹数量的比值不变，解理倾角对岩石的微观张拉、剪切破坏机理无明显影响.

（4）颗粒级别的晶粒解理特征对硬质岩石的力学性质、破坏过程有重要影响，板裂、岩爆等深部问题的孕育过程、破坏烈度也应考虑晶粒内部解理特征，特别是在具有解理结构矿物颗粒含量较高且颗粒本身性质对岩石性质响应影响也显著的条件下，晶粒内部解理特征更是应该引起注意.