三轴应力下颗粒流失对断层破碎带凝灰岩渗流特征的影响
2022-06-16黄昌富张帅龙高永涛吴顺川王文强卢庆钊
黄昌富,张帅龙,高永涛✉,吴顺川,周 喻,孙 浩,王文强,卢庆钊
1) 北京科技大学土木与资源工程学院,北京 100083 2) 昆明理工大学国土资源工程学院,昆明 650093 3) 河南理工大学能源科学与工程学院,焦作 454000 4) 中铁十六局集团第一工程有限公司,北京 101300
目前,断层破碎带岩体渗流演化机制逐渐成为岩石力学界研究和关注的热点之一.作为诱发突水灾害的内因,断层破碎带岩体在三轴应力下的变形与渗流特性对隧道施工安全具有重要影响[1−2].其次,破碎岩石孔隙率较大,其渗透性比完整岩石大数个量级,由渗流引起的重大灾害事故多发生于此[3].因此,研究颗粒流失下断层破碎带岩体孔隙结构及渗流流速时变演化规律对隧道水害防治具有重要的现实意义和工程指导价值.
近年来,国内外学者对破碎岩体的渗流演化规律进行了大量的研究.缪协兴等[4],陈占清等[5]利用破碎岩石压实渗透仪开展了不同岩性破碎岩体的渗透试验,得到了岩体渗透特性的变化规律.孙明贵等[6]在石灰岩应力−应变非Darcy流渗透特性试验基础上建立了一种测定岩石渗透特性的动力学模型.王伟等[7]开展低渗透岩石三轴渗流−应力耦合试验,最终得出了围压和渗压作用下岩石体积应变与渗透率之间的关系式.杜锋等[8]通过自制多孔介质水沙两相渗流试验系统对突水溃沙机理进行研究,得到了多孔介质孔隙度、破碎岩石粒径及沙粒粒径等因素对水沙流动规律的影响.姚邦华[9]利用自制破碎岩体渗透试验系统开展了破碎岩体变质量渗流试验研究,得到了配比、轴向应力、含沙量及颗粒迁移等因素对渗流突变的影响.Liu等[10]基于稳态渗流法,研究了三种破碎岩石的渗透特性,提出了用置信区间描述渗透系数的三种方法.Ma 等[11−13],张天军等[14−16]利用万能试验机、渗透仪研究了不同级别位移、不同水压及不同配比条件下的破碎岩石渗透特性,得到了多项渗透参数在渗透失稳过程中的变化规律.张勃阳等[17−18]开展陷落柱取样,研究破碎岩体渗透特性,得到了陷落柱渗流突变机制与渗流特性.Feng等[19]开展破碎岩体渗透试验研究,得到了不同Talbot幂指数n值下破碎岩体质量流失与渗透率的关系.杨斌等[20]基于Forchheimer定律采用钢球模拟堆积破碎岩体,开展了高速非线性渗流试验,揭示了颗粒粒径与非线性渗流模型参数的关系.Yu等[21]开展胶结破碎岩石渗透试验研究,探讨了陷落柱的阻水性能与影响因素.刘伟韬等[22]开展三轴压缩条件下渗流试验,得到了陷落柱骨架砂岩在不同围压及渗透压条件下的力学性质、渗流特性和声发射基本特征.Wasantha和Ranjith[23]在考虑围压的基础上,开展不同含水条件下霍克斯伯里砂岩三轴压缩试验,得到了不同围压条件下水对霍克斯伯里砂岩力学行为的影响.Zhao[24]等研究了不同粒径破碎岩石在轴向应力下的渗流特性参数变化规律.李玉寿等[25]研究了煤样在三轴应力及孔隙水作用下的变形和声发射特性.颜丙乾等[26]总结了国内外多场耦合多尺度力学试验设备的改进和研发、数值模拟软件及耦合计算程序的开发等方面的研究现状.
目前,关于破碎岩体渗流演化规律的研究成果多集中于堆石坝、陷落柱、巷道等方面,对于断层的研究较少,且由于现场取样难度高,试样多为人为配制[27−28].此外,为解决密封问题,破碎岩石渗透试验多采用侧限性渗透仪开展研究[29].然而,实际地下工程中的破碎岩体基本赋存于三轴应力条件下,仅考虑轴压而在一定程度上忽略围压将使渗流试验结果产生较大误差,但能够实现围压可调的三轴承压破碎岩石渗透测试或模拟设备还相当缺乏[15],影响到该类(破碎)岩石工程问题的深入研究.因此,笔者开展原位取样工作,运用可调节围压的三轴渗流试验系统,研究了不同颗粒级配破碎凝灰岩相似材料在不同级别三轴应力条件下渗透前后的孔隙结构及渗流流速时变演化规律,以期为断层破碎带突水问题提供必要的理论依据.
1 试样制备及试验设备
1.1 试样选取及制备
试样取自福建—厦门高速铁路项目(福厦高铁)碧峰寺隧道F3断层内部(图1),该断层产状为28°∠88°,沟通了地表冲沟与地下含水层,断层带区域隧道埋深约为100 m,掌子面实测水压值为0.58~0.76 MPa,断层风化破碎晶屑凝灰岩密度为2037 kg·m−3.

图1 碧峰寺隧道F3断层破碎带Fig.1 Bifeng temple tunnel F3 fault fracture zone
开展XRD(X-ray Diffraction)衍射试验,定量分析了断层破碎带风化凝灰岩的矿物成分,如图2所示.断层凝灰岩的主要成分为坚硬耐磨的石英(质量分数为9.1%),硬度略低于石英的钠长石(质量分数为11.1%)、正长石(质量分数为5.1%)、钙长石(质量分数为39.4%)以及白云母(质量分数为35.3%)等矿物质.

图2 断层破碎带凝灰岩试样X射线衍射结果.(a) D8 AdvanceX射线衍射仪; (b) 衍射强度图谱; (c)矿物成分含量Fig.2 X-ray diffraction results of tuff samples from fault fracture zone: (a) D8 Advance X-ray diffractometer; (b) diffraction intensity map; (c) mineral content
通过现场考察(图1),发现F3断层破碎带由不同粒径强风化破碎凝灰岩块弱固结而成.根据前人研究,室内破碎岩石试验中,不同粒径破碎岩石的多重质量比构成了高维参数空间,导致了维数灾难[30].通过现场观察和筛分试验可知,F3断层带内破碎凝灰岩的粒径分布具有连续性和统计意义上的自相似性,因此可采用分形几何来定量描述其级配分布[31−32].
根据分形理论模型[33],破碎岩石颗粒数量满足

其中:N为颗粒数量;k为常数;d为颗粒粒径,m;D为破碎分形颗粒集合体的分形维数.
由式(1)可知颗粒数量N与粒径d存在对应关系,颗粒质量M与颗粒数量N满足如下关系
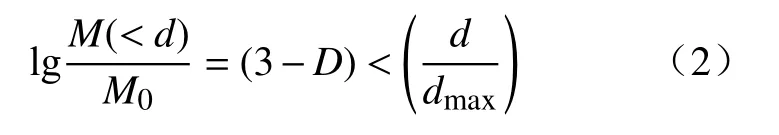
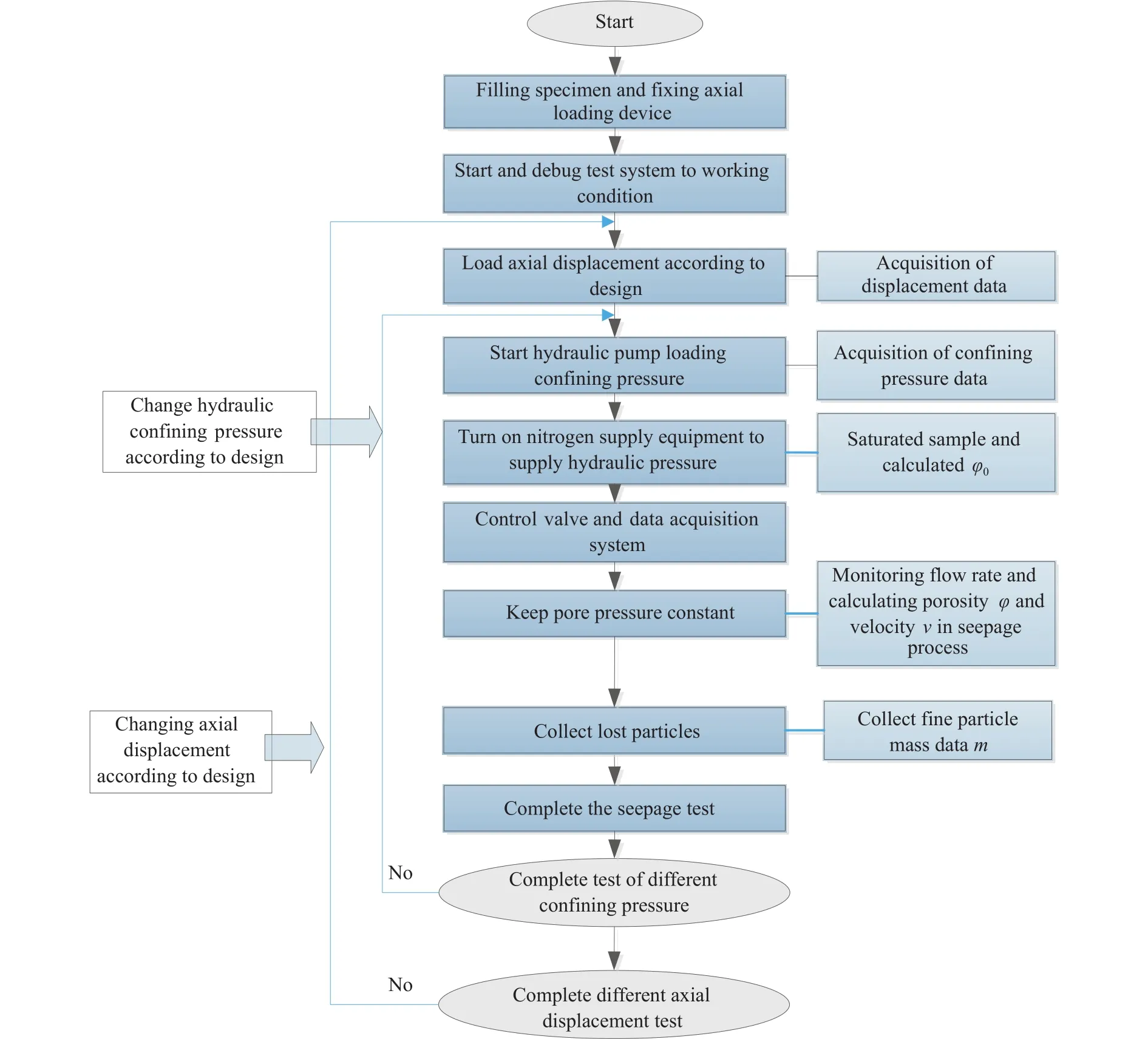
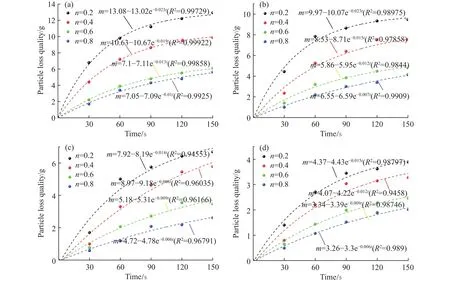
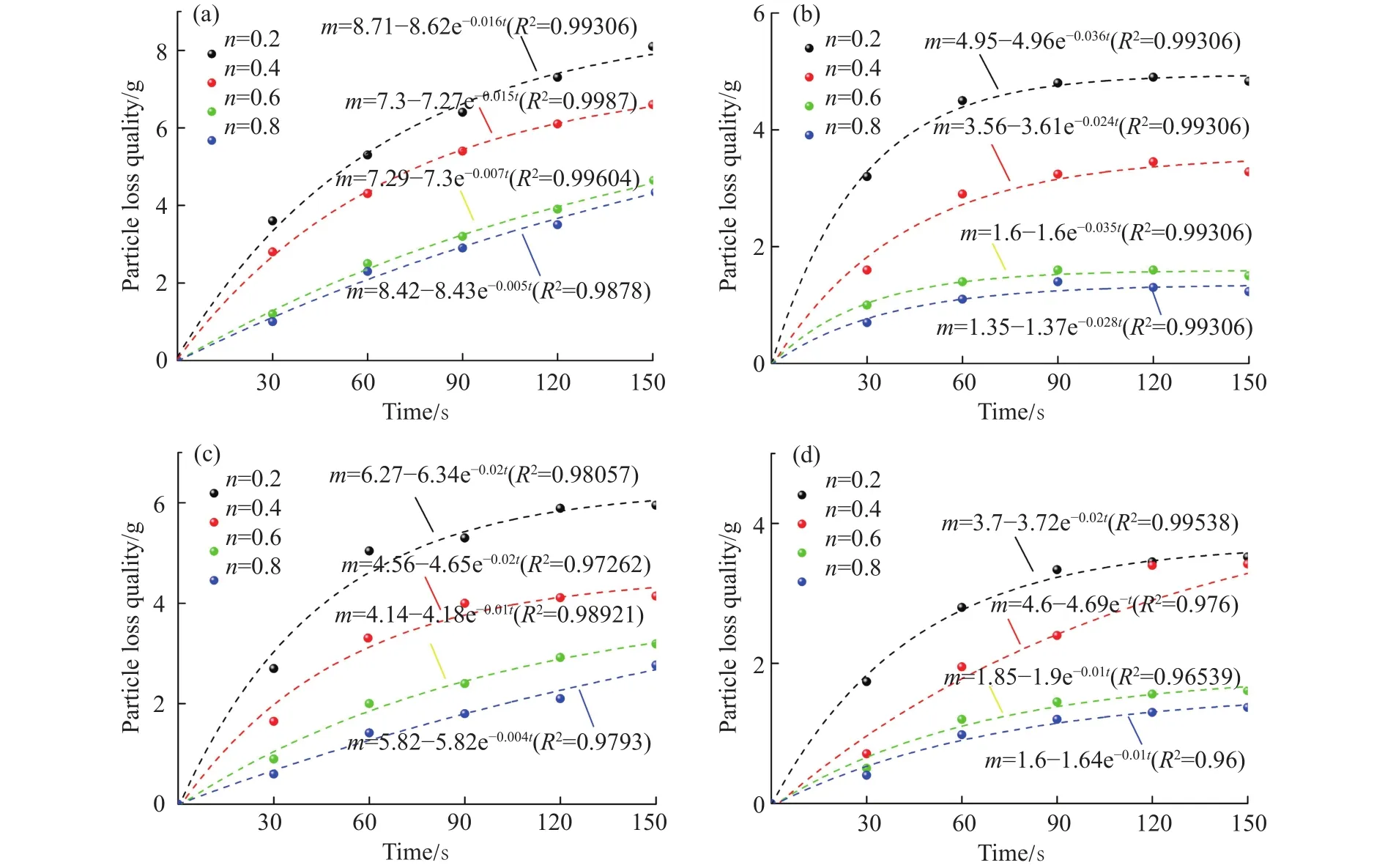
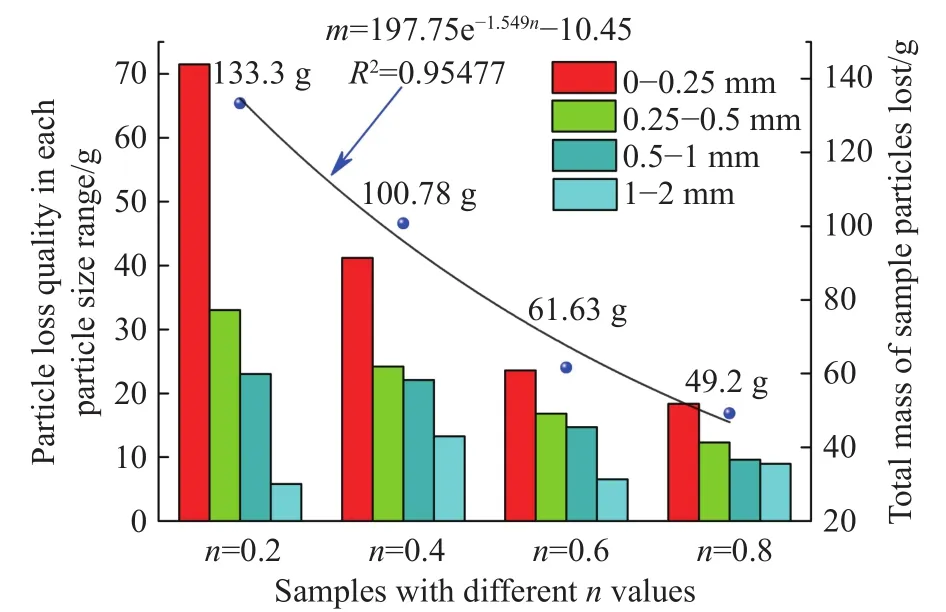
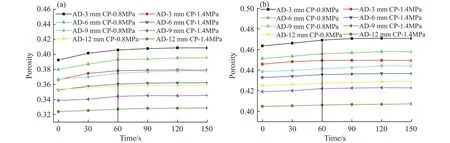
其中:M( 因此,符合分形级配的破碎岩石颗粒级配方程可表示为 其中:p0(d≤di)为尺寸小于di的凝灰岩颗粒原始质量比;di为第i组中最大颗粒尺寸,mm;dM为凝灰岩颗粒最大尺寸,mm.将(3−D)代换为n,则公式(3)即为 Talbot级配理论模型[34−35] 通过改变 Talbot 幂指数n值(简称n值)可以实现颗粒级配对破碎岩石渗流特性影响的研究目的. 为了减小尺寸效应的影响[33],破碎凝灰岩样最大直径取内套筒内径(50 mm)的1/5[36−37],即10 mm.采用颚式破碎机破碎断层凝灰岩块,利用标准振动筛机筛选出6种粒径区间(0~0.25 mm、0.25~0.5 mm、0.5~1 mm、1~2 mm、2~5 mm、5~10 mm)的破碎晶屑凝灰岩颗粒,如图3所示.如图3所示. 图3 各粒径区间破碎凝灰岩试样Fig.3 Fractured tuff samples in various particle size ranges 试验采用的破碎岩石三轴渗流试验系统(TSS-01)主要由水压与围压加载控制系统A、数据采集系统B及破碎岩石三轴渗透仪C组成,如图4所示.该系统能够提供稳定可调的高精度渗透水压(0~3 MPa)与围压(0~10 MPa).其中,三轴渗透仪作为该系统的核心,主要由轴向位移加载装置(一体式反力框架结构)、柔性内套筒、上下活动密封压头等组成.破碎岩石试样能够在轴向位移与围压作用下发生形变,从而实现三轴应力的定量加载. 图4 破碎岩石三轴渗流试验系统及示意图.(a)实物图; (b)原理示意图Fig.4 Schematic diagram of triaxial permeability testing system for fractured rock: (a) physical map; (b) schematic diagram of principle 从F3断层破碎带取样,开展现场筛分试验,得到不同粒径区间对应的岩块数目,根据筛分试验结果与公式(2)可确定(M( 表1 不同Talbot幂指数n值下的岩石颗粒质量Table 1 Rock particle mass under different n 本次试验加载方式采用轴向位移控制法[15].为减小每组试样间的误差和离散性,保证相同级配试样具有相同的初始孔隙度,试验采用分层装填法和高度控制法,即相同级配试样分3次(层)装填,且每层高度一致.试验方案(图5)考虑颗粒粒径级配、三轴荷载、孔隙水压等因素对破碎岩石渗透特性的影响,先后施加轴向位移和围压调控不同级配破碎凝灰岩的孔隙率.受多级别三轴应力影响,散体状破碎凝灰岩颗粒的排列方式将产生阶段性变化,其孔隙率与渗透性均会相应改变.待三轴压力恒定后,开启渗透压力加载系统,通过数据采集系统调节并记录试验过程中的流量数据,并按照试验方案定时收集试验过程中迁移流失的细小颗粒. 根据前人研究,破碎岩样轴向加载方式可分为轴向位移控制法和轴向应力控制法两大类[14−15,27],两类加载方式的原理均是通过定量施加应力来改变和调控散体破碎岩石试样的孔隙率.本次试验所采用的试验系统适合应用轴向位移控制法.因此,考虑围压作用,试验设计4级轴向位移,分别为3、6、9、12 mm,加载至位移能够保持恒定方可停止加载,轴向位移与试样高度均采用高精度激光测距仪量测记录.位移加载完毕后,打开渗透压力控制系统对试样进行低压供水排气饱和(水压p< 0.05 MPa),保证试样结构不被破坏,饱和时长为10 min.每级轴向位移下设2级围压,通过液压手动泵进行预设,考虑F3断层带赋存参数,预设值分别为0.8和1.4 MPa,期间不卸载,每级围压加载时长为60 s.试验采用稳态渗流法,为保证孔隙水从破碎岩样孔隙内部通过,围压必须比孔隙水压大0.2~0.8 MPa.因此,考虑隧址断层埋深情况,0.8 MPa与1.4 MPa围压下设0.6 MPa水压. 试验前,首先将设备调试至正常工作状态,固定渗透仪至垂直状态,同时在渗透仪套筒内部涂上厚度为3 mm的凡士林以消除边壁效应的影响[38−39],从而解决试验过程中水流沿边壁较大孔隙流失的关键问题.然后,根据渗透仪容积选取240 g不同级配破碎岩石试样装入套筒内,按照图5所示试验流程进行破碎凝灰岩渗透试验.试验前对试样表面进行平整处理,确保轴向位移加载装置对试样施加的是垂向载荷. 图5 三轴破碎凝灰岩渗流试验流程图Fig.5 Triaxial broken tuff seepage experiment flow chart 渗透过程中,各级三轴应力下每隔30 s收集一次流失的细小颗粒,对收集到的颗粒进行编号、干燥、筛分和称重.考虑到过滤水中依然存在细小流失颗粒的可能性,因此将过滤水按照同样的方法分次收集、编号、沉积、烘干、称量细小颗粒质量.对于不同级配试样在不同级别轴向位移下的颗粒流失质量−时间试验结果,通过非线性拟合,可用如下函数关系式进行描述: 其中:m为不同Talbot幂指数n值试样在不同级别轴向位移下颗粒流失质量,g;a、b、c为拟合参数;t为试验时长,s;e为指数型函数的底数. 如图6所示,拟合曲线的拟合度均高于94%,因此可用此函数对不同n值试样在不同级别轴向位移下的颗粒流失质量−时间关系进行描述. 图6 不同轴向位移下流失颗粒质量−时间拟合曲线.(a)轴向位移为3 mm; (b)轴向位移为6 mm; (c)轴向位移为9 mm; (d)轴向位移为12 mmFig.6 Lost particles mass-time fitting curve under different axial displacements: (a) axial displacement is 3 mm; (b) axial displacement is 6 mm; (c) axial displacement is 9 mm; (d) axial displacement is 12 mm 从图6中可以看出,由于试样中不同粒径区间颗粒分布的随机性与颗粒受轴向应力破坏后孔隙结构的离散性和不可预测性,同一n值下试样的流失颗粒质量并不随着三轴应力的增加而单调变化.拟合曲线随着n值的增加而变缓,表现为流失颗粒减少、流失时间增长.这是由于n值越大,粗颗粒占比越大,相同质量试样的装填高度也越大,因此,在相同的轴向应力作用下,较大的孔隙结构所形成的突水通道能够平稳运移出更多细小颗粒;相反,n值越小,充填于大颗粒孔隙间的细小颗粒越多,此时试样密实度大,渗透性差,试样两端渗透压差大,大量的细小颗粒最终无法承受水压而在短时间内随水冲出,发生渗流突变,这也可以在一定程度上解释断层破碎带渗透失稳灾害的突发性.此外,从图中可以看出,n=0.4与n=0.6之间存在较大差值.该现象说明级配越大,流失的细小颗粒越少,n=0.4~0.6之间存在着最佳级配点[16]. 以轴向位移为3 mm和6 mm为例,在平面直角坐标系中绘制同级轴向位移不同围压情况下的流失颗粒质量−时间散点图,并用公式(5)拟合关系曲线,如图7所示,拟合度均高于96%.从图中可以看出,拟合曲线随围压增大而变缓,流失质量整体减小.这是因为破碎试样在围压作用下发生径向变形,粗颗粒与充填在粗颗粒孔隙间的细小颗粒被径向压密,孔隙的连通性减弱,突水通道受阻,细小颗粒需要克服更大的阻力才能流失.此外,通过对比相同围压不同轴向位移的拟合曲线,可以看出轴向位移越大,颗粒流失质量随围压减小的幅度越小.这是由于前期较小的轴向位移下,试样孔隙较多,此时孔隙在围压作用下能够迅速调整,流失颗粒质量变化较大;随着轴向位移增大,试样内部孔隙调整趋于缓和,突水通道只能在围压的作用下产生较小的改变,从而表现为试样流失颗粒质量拟合曲线变化平稳的趋势. 图7 不同围压下流失颗粒质量−时间拟合曲线.(a) 轴向位移为3 mm,围压为0.8 MPa; (b) 轴向位移为3 mm,围压为1.4 MPa; (c) 轴向位移为6 mm,围压为0.8 MPa; (d) 轴向位移为6 mm,围压为1.4 MPaFig.7 Lost particles mass-time fitting curve under different confining pressures: (a) axial displacement is 3 mm, confining pressure is 0.8 MPa; (b) axial displacement is 3 mm, confining pressure is 1.4 MPa; (c) axial displacement is 6 mm, confining pressure is 0.8 MPa; (d) axial displacement is 6 mm,confining pressure is 1.4 MPa 渗透试验中,不同轴向位移与围压下,各粒径区间流失颗粒质量、流失颗粒总质量与n值的关系如图8所示,图中柱状图代表不同粒径区间流失颗粒质量,蓝色全球及其拟合曲线代表试样流失颗粒总质量.由图8可看出,渗透试验中粒径区间量级越小,流失质量占比越大,且各粒径区间流失质量随幂指数n值增大而减小.其中,0~0.25 mm粒径区间的细小颗粒流失量最大,对应n=0.2、0.4、0.6、0.8时,其流失质量分别为 71.5、41.2、23.6和18.36 g,与表1对比可知,占原始试样对应粒径区间含量的62.3%,75.1%,90%,146.3%,可以看出占比越来越大.n=0.8时,流失量高于原始含量,这是由于三轴应力和渗透水压对试样中大粒径岩粒产生更加显著的挤压破碎、冲蚀、磨蚀等作用,因而产生更多的次生细小颗粒,最终导致0~0.25 mm区间细小颗粒流失量超过原始含量的现象.此外,试样流失颗粒总质量与n值的试验结果也可用式(5)进行非线性拟合,拟合度高达95.5%. 图8 流失颗粒质量与n值关系Fig.8 Relationship between mass of lost particles and n value 将级配混合试样装入渗透仪内套筒后,测得其初始堆积高度hi(h1=11.2 cm,h2=11.6 cm,h3=12.1 cm,h4=12.9 cm),则与之对应的初始孔隙率分别为φ1=0.277、φ2=0.325、φ3=0.375、φ4=0.411.各级轴向位移与各级围压使试样产生不同程度的轴向变形与径向变形.根据排水法,受围压影响所排出的液体体积ΔVi(cm3)即为围压引起的试样减小体积,ΔVi由出口量筒收集记录.此时,渗透前各级轴向位移与围压下的试样体积V0′可通过下式求得: 其中:r0为内套筒初始半径,cm;h0为破碎凝灰岩试样的初始高度,cm;Δh为轴向位移,cm;ΔVi为每级围压下渗透液排出体积,cm3;i代表围压级数. 此时,受各级荷载作用后的试样孔隙率为 其中:V0为凝灰岩破碎前的体积,m3;V0=m/ρ0.m为凝灰岩破碎前的质量,kg;ρ0为凝灰岩破碎前的密度,kg·m−3;h为不同轴向位移条件下的试样高度,h=hi−Δh. 渗流过程中试样发生颗粒流失,其孔隙率发生变化,可通过式(8)求得渗透过程中每个时间段的孔隙率 其中:Δmj为j时刻记录的颗粒流失质量,g,j代表以30 s为间隔的时刻,即j=1代表30 s时,j=2代表60 s时,以此类推;A为各级荷载下试样渗流过程中的截面积,cm2,可由式(9)计算 以n=0.2和n=0.6两种级配试样为例,绘制三轴应力下不同级配试样渗透过程中孔隙率−时间关系曲线,如图9所示. 图9 三轴应力下不同级配试样渗透过程中孔隙率−时间试验结果(图中AD指轴向位移,CP指围压).(a)n=0.2; (b)n=0.6Fig.9 Porosity-time test results of specimens with different gradations during infiltration under triaxial stress (AD means axial displacement, CP means confining pressure): (a) n=0.2; (b) n=0.6 考虑n值对孔隙率变化规律的影响.由图9可得,两种级配试样均可以60 s作为曲线拐点,划分为快速增长阶段(0~60 s)和缓慢变化阶段(60~150 s),与流失质量时变规律相对应.快速增长阶段,孔隙率时变曲线随n值的增加而变缓,n=0.2时,轴向位移为3 mm、围压为0.8 MPa条件下,试样在60 s与0 s处的孔隙率差值为0.013,而n=0.6时,相同条件下试样60 s与0 s处的孔隙率差值为0.006.可见,n值越小,孔隙率越小,孔隙率增长幅度越大.这是由于随着n值的增加,试样可流失颗粒质量减少,粗颗粒占比增大且不易产生大变形,因此孔隙率较大,变化幅度相对缓慢.试样孔隙率极大值集中在缓慢变化阶段(60~150 s),该阶段粗颗粒及其孔隙结构保持相对稳定状态. 考虑轴向位移与围压对孔隙率变化规律的影响.由图9可得,相同n值下试样的孔隙率随轴向位移与围压的增加而减小.具体而言,相同围压条件下,孔隙率大小关系为轴向位移3 mm > 6 mm >9 mm > 12 mm;同级轴向位移下,围压为0.8 MPa的孔隙率大于围压为1.4 MPa的孔隙率.由此可见,破碎岩石渗透试验不能简化和忽略围压的作用.开展破碎岩石三轴渗透试验,考虑轴压与围压的共同作用,对孔隙率的研究具有重要的现实意义. 可从宏−细观两方面分析造成上述现象的原因.宏观方面[9,16],试样被渗透前不同级别的三轴应力作用于自然松散堆积的破碎岩石试样,岩石颗粒之间发生刚体相对运动与棱角接触性破碎现象,颗粒发生位移重组,多数粗颗粒由点−点接触变为面−面接触,破碎岩石试样内部孔隙结构迂曲度在粗颗粒劣化的影响下增大;试样被渗透后,骨架结构间细小颗粒在渗流冲刷作用下异位,最终随着粗颗粒的平衡充填于大小不一的孔隙中,如图10所示. 图10 渗透试验前后级配颗粒岩样宏−细观特征.(a)渗透试验前颗粒特征; (b) 渗透试验后颗粒特征Fig.10 Macro-meso characteristics of granular rock samples before and after the permeation test: (a) particle characteristics before the penetration test; (b) particle characteristics after the penetration test. 细观方面,单个岩石粗颗粒在三轴应力和渗流冲刷的综合作用下破裂、破碎和研磨,产生不同粒径的次生细小颗粒.渗透过程中,水流不仅会裹挟细小颗粒迁移流失,同时会对暴露于孔隙中的破碎岩石表面产生冲蚀和磨蚀效应,一方面产生更多次生细小颗粒,另一方面,细小颗粒的迁移流失与持续作用的围压不断调整残余粗颗粒位置及孔隙结构,最终试样产生塑性变形并形成稳定的导水通道[40].为验证颗粒岩样在三轴渗透作用下的演化机理分析的正确性,对试验后的颗粒进行烘干—筛分—称重,与试验前各粒径区间质量对比(表1),记录并绘制试验后不同n值级配试样各粒径区间质量变化图,如图11所示.由图11可知,破碎凝灰岩样在三轴应力和渗流作用下表现为“粗颗粒(粒径区间为2~10 mm)质量减少,细小颗粒(粒径区间为0~1 mm)质量增加”的规律,该现象解释了次生颗粒的来源,同时验证了宏−细观机理分析的合理性.综合试验观测与数据分析,三轴应力下破碎岩石渗透宏−细观演化机理如图12所示,图中展示了宏观方面的“松散堆积、位移重组、破碎充填”机制以及“破裂、破碎、研磨”等细观机制. 图11 试验后不同n值级配试样各粒径区间质量变化(正值为增加,负值为减少)Fig.11 The mass change of each particle size interval of samples with different n-value gradations after the test (+ indicates increased, −indicates decreased) 图12 三轴应力下破碎岩石渗透演化过程Fig.12 Seepage evolution process of broken rock under triaxial stress 利用数据采集器每隔10 s采集流经破碎凝灰岩试样的体积流量Q(cm3),每组试样采集15次,共计 150 s,通过式(10)计算渗流速度v(cm·s−1): 不同n值试样渗透试验中流速−时间关系如图13所示.从图13中可以看出,流速v随n值的增大而整体增大,可见流速大小与试样中细小颗粒占比有关.此外,从图中还可以看出,流速时变曲线可分为初始阶段、突增阶段及缓变阶段.围压为0.8 MPa时各阶段流速整体大于围压为1.4 MPa时对应阶段的流速.初始阶段特征表现为历时短、流速低等.图13(a)中观察到试样轴向位移为3 mm与6 mm时,流速在0~30 s与150~180 s之间下降,原因是高级别轴压下细小颗粒更加致密,在渗流初期堵塞了孔隙结构与出水口.对比图13(a)~(d)发现,初始阶段随着n值增加而减少,n=0.8围压为0.8 MPa时,试样不存在初始阶段,在10 s时流速即达到峰值.这是因为n值较大且围压较小时,细小颗粒占比减少,组合也不够密实,因此发生细小颗粒堵塞突水通道的现象也相对减少,初始阶段现象不明显甚至消失.随着渗流时间增加,堵塞的细小颗粒无法承受渗透压力,水流冲散并卷走孔隙内与出水口处的细小颗粒,发生喷溅现象,以0~2 mm粒径区间的颗粒为主,偶见2~4 mm粒径区间的粗颗粒.水流喷溅现象发生后,流速进入缓变阶段,该阶段对应颗粒缓慢流失阶段,此时试样已基本形成稳定的孔隙结构与导水通道,流速高且稳定.观察图13可发现平稳阶段的流速偶尔发生波动,原因可能是试样内部孔隙结构微调过程中,迁移颗粒偶尔会堵塞现有突水通道,在较大的渗透水压下,堵塞颗粒很快被高压水流冲开,因此表现为流速时变曲线上下波动.由此可见,隧道断层突水过程中,突水量偶尔减小并不意味着危险程度下降,反而可能是因为岩块暂时堵塞突水通道产生突水量减小的假象,这种情况下需及时做好预防措施,以防水压积聚增高造成更为猛烈的二次灾害. 图13 不同n值级配试样渗透试验中流速−时间试验结果(图中AD指轴向位移, CP指围压).(a) n=0.2; (b) n=0.4; (c) n=0.6; (d) n=0.8Fig.13 Flow velocity-time test results of different Talbot power exponent gradation samples in penetration test (AD means axial displacement, CP means confining pressure): (a) n=0.2; (b) n=0.4; (c) n=0.6; (d) n=0.8 综合分析颗粒流失、孔隙率及流速试验结果,可判定颗粒流失为破碎凝灰岩突水灾害的内因,而三轴应力和流水渗透作用为破碎凝灰岩突水灾害的外因.在内外因综合作用下,破碎凝灰岩渗流流速时变演化过程表现出不同的阶段和形态,整个过程可分为“平稳渗流、渗流流速突增和近似管流”三个阶段.平稳渗流阶段是破碎凝灰岩突水的孕育阶段,试样内部骨架与孔隙结构在水流趋势下逐渐膨胀、扩展、恶化,细小颗粒在水流作用下沿着孔隙从入水口向出水口运移,此时水流较小,细小颗粒流失较少,浑浊度不高;当破碎凝灰岩颗粒内部的细小颗粒无法承受当前渗透压力时,大量细小颗粒在短时间内随水渗流而出,渗流流速突增,进而引发试样内部粗颗粒位移、孔隙结构打开、导水通道贯通等链式渗流灾变,渗流流速突增阶段水流浑浊度最高;突水通道完全形成后,渗流状态转变为近似管流阶段,该阶段偶尔有残存的细小颗粒和次生颗粒流失,试样流速趋于稳定,如图14所示.F3断层带突水灾害发生发展过程与试验中的三个阶段相对应:由图14可知,F3断层带突水灾害爆发前,多股水流沿掌子面裂隙渗流而出,水质较清澈,水流速度与流量不断增大,与试验中的“平稳渗流阶段”相似;F3断层带突水灾害爆发过程中,水流流速与流量猛增,短时间内达到峰值,且水质浑浊,夹杂细小粒径破碎岩石,掌子面在短时间内被淹没,与试验中“渗流流速突增阶段”相对应;由于现场断层带内水体静储量与动储量有限,加之现场实施了一定的堵/排水措施,在突水灾害后期,流量、流速及浑浊度不断下降,而试验中由于采用稳态水压补给导致渗流速度未减弱,出现了“近似管流”的现象.综上所述,破碎岩石三轴渗流试验结果能够较好地揭示F3断层带突水灾害的突水模式及渗流时变演化规律,验证了试验方法与试验结果的可靠性. 图14 三轴渗透试验与F3断层突水演化过程Fig.14 Triaxial permeability test and water inrush evolution process of F3 fault 地下工程施工过程中能否发生断层突水灾害,主要取决于断层内破碎岩石的渗透特性.本文开展现场断层取样,利用破碎岩石三轴渗流试验系统对断层破碎带凝灰岩进行了不同三轴压力及渗透压力条件下的三轴渗流压缩试验,研究并分析了试验过程中不同粒径级配试样的颗粒流失规律、孔隙结构及渗流流速时变演化规律.得出的主要结论如下: (1)各级配试样在不同轴向位移与围压下的流失颗粒质量与时间可用指数型经验公式拟合,拟合度不低于94%.曲线随着n值的增加而变缓,n=0.4~0.6之间存在着最佳级配点,即断层破碎带破碎程度越高,突水灾害的烈度和危险程度越高.n值相同时,轴向位移和围压均与流失颗粒质量成反比,且轴向位移越大,颗粒流失质量随围压减小的幅度越小. (2)由于颗粒的规律性流失,试样孔隙率经历了初期快速增长阶段和后期缓慢变化阶段,且孔隙率量级为0.33~0.52.孔隙率随n值增大而增大,随轴向位移与围压的增大而减小,简化或忽略围压将导致较大误差. (3)不同级配n值试样的流速时变曲线可划分为初始阶段、突增阶段及平稳阶段,分别对应破碎凝灰岩渗流流速时变演化过程中的“平稳渗流、渗流流速突增和近似管流”三个阶段.围压为0.8 MPa时各阶段流速整体大于围压为1.4 MPa时对应阶段的流速.需制定有效措施预防断层突水灾害过程中由于细小岩块堵塞突水通道而引发的二次灾害.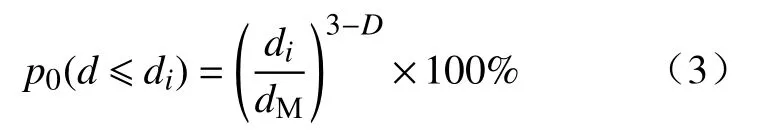
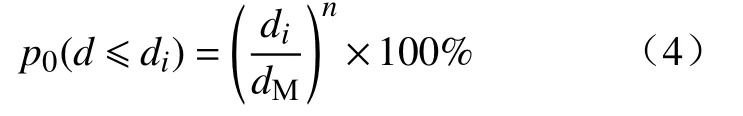

1.2 试验系统及功能

1.3 试验方案及流程

2 试验结果分析及验证
2.1 颗粒流失规律

2.2 三轴应力下颗粒流失对孔隙结构的影响

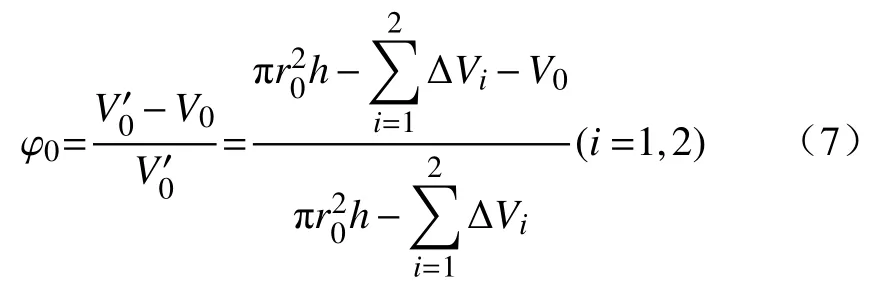

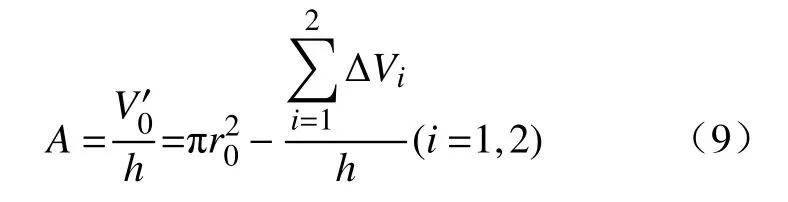



2.3 颗粒流失对破碎凝灰岩流速时变规律的影响



3 结论
