适应多端直流输电系统直流故障仿真的工程实用模型研究

郑 伟，国建宝，杨光源，曹润斌，聂少雄，李桂源

适应多端直流输电系统直流故障仿真的工程实用模型研究

郑 伟1，国建宝1，杨光源1，曹润斌2，聂少雄2，李桂源2

(1.中国南方电网有限责任公司超高压输电公司检修试验中心，广东 广州 510080；2.南方电网科学研究院有限责任公司，广东 广州 510080)

多端直流输电(Multi-terminal DC, MTDC)已经成为颇具竞争力的跨区域大功率输电技术，但因结构复杂，目前缺乏完整的数学模型。真双极混合桥模块化多电平变流器(Modular multi-level converter, MMC)是特高压MTDC的重要部分。若仍沿用半桥MMC的模型建模，真双极结构中双阀组交流侧的电气联接无法体现。另外，半桥MMC模型中0-1二值开关函数推广到混合桥的合理性也有待证明。为解决MTDC建模中存在的上述问题，以昆柳龙直流工程为例，首先推导真双极混合桥MMC的完整数学模型，并对常规高压直流换流站和直流传输线进行准稳态和集中参数近似。进一步建立了直流故障下MTDC的工程实用数学模型，兼顾了精确性和复杂性。最后针对直流单极接地故障运用该模型进行分析计算，并与PSACD仿真结果进行对比，验证了所提出模型的有效性。

多端直流输电；模块化多电平变流器；真双极混合桥；电磁暂态仿真；昆柳龙直流工程

0 引言

多端直流输电(Multi-Terminal DC, MTDC)技术具有优化潮流、改善系统稳定性等特点[1]，适用于大规模海上风电并网[2-3]、构建直流互联电网[4]以及跨区域大功率输送[5]等多类应用场景。南方电网设计并建设了世界首个多端混合特高压直流工程——昆柳龙直流工程。

以昆柳龙直流工程为代表的MTDC拓扑结构复杂、控制器繁多，且同时包含电网换相变流器(Line-Commutated Converter, LCC)和由真双极混合子模块(Hybrid Sub-Module, HSM)构成的模块化多电平变流器(Modular Multi-Level Converter, MMC)。现有文献缺乏对MTDC全系统电磁暂态仿真模型的详细推导，多以单个变流器模型为主。

LCC的仿真模型可划分为准稳态模型[6-7]、动态相量模型[8]和电磁暂态模型[9]。准稳态模型计算量最小，虽然精确度不如电磁暂态模型和动态相量模型[10]，但能适用于直流故障情景下的工程近似。动态相量模型和电磁暂态模型精确度更高，但计算量大幅增加，不利于MTDC在全系统仿真中的应用。在分析直流系统故障工况下的行为特征时，合适的仿真模型有利于平衡模型的精确性和复杂性[11]，并且有助于继电保护设计[12]。

MMC的仿真模型可分为器件详细模型[13]、器件简化模型[14]、可变电阻模型[15]和平均值模型[16]。器件详细模型精确度最高，但过于复杂，难以应用于大系统场景。虽然器件简化模型和可变电阻模型计算量有所降低，但在含多变流器的MTDC仿真中，仍然会带来巨大的计算负荷。平均值模型将桥臂子模块看作等效电压源，计算量最小，且能满足MTDC直流故障仿真工程精度要求。

目前学术界对MMC仿真模型的研究多以半桥MMC为主。真双极HSM-MMC[17]作为MMC的复杂形式，对其仿真模型的研究[18-20]较少，通常直接沿用半桥单体MMC的平均值模型，再按真双极连接方式进行组合。这类推导方法并未体现两个单体MMC在交流侧的电气耦合关系。由于混合桥MMC中存在输出负电压的全桥子模块，因此半桥子模块的0-1二值开关函数概念也不再适用。现有建模方法未对“开关函数”这一概念沿用至混合桥MMC的合理性进行解释，存在一定的逻辑瑕疵。

针对以上问题，本文以实际运行的昆柳龙MTDC为例，首先完整推导了真双极HSM-MMC在静止和同步坐标系下的数学模型，并严格推导了半桥子模块开关函数向HSM-MMC推广的合理性。然后对双阀组串联结构的LCC采用计算量最小的准稳态模型，并忽略了交直流滤波器等对直流故障过程影响不显著的部分。进一步将MTDC中直流传输线等效为考虑互感的一对集中参数阻感支路，兼顾了精确性与复杂性，避免采用贝瑞龙模型[21]或电报方程[22]带来的繁琐计算。最后对比分析了本文所提出模型的计算结果与电磁暂态仿真软件PSCAD得到结果，验证了所提模型的有效性。

以此为基础建立的直流故障下MTDC的工程实用仿真模型，填补了特高压场景下复杂拓扑MMC和LCC数学建模的空白。

1 双极混合桥MMC数学模型

在MTDC中，混合桥臂真双极MMC的桥臂由半桥子模块(Half-Bridge Sub-Module, HBSM)和全桥子模块(Full-Bridge Sub-Module, FBSM)构成，该类型MMC的主电路和控制系统比一般半桥伪双极MMC复杂。本文将其简称为“特高压MMC”，其主电路如图1所示。

图1 特高压MMC主电路

1.1 真双极混合桥MMC的数学模型

图1为MTDC中正极侧的真双极MMC，上下两部分变流器电气量近似相同，符号解释见表1。

表1 真双极MMC符号表

半部分变流器的三相上、下桥臂电压方程为

式(1)中两分式相减，得到交流方程式(3)。

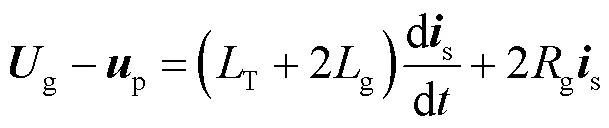
联立式(3)、式(5)，得到交流基本方程式(6)。

式(2)和式(6)并称为MMC主电路基本方程。

1.2 混合桥臂基本方程

式(7)、式(8)两边分别求和再相加，得到

联立式(9)—式(11)并化简，得到

1.3 同步坐标系下MMC数学模型

主电路基本方程是在旋转坐标系下对MMC电磁特性的描述，混合桥臂基本方程给出了桥臂的伏安特性。结合下文有关电气量的基本假设和Park变换，可以得到同步坐标系下MMC的数学模型。

以sub-MMC1中A相为例，说明MMC电气量的基本假设。

假设1 上、下桥臂的开关函数的直流分量相等、基频交流分量幅值相同、相位相反。

假设2 上、下桥臂电流的直流分量相等、基频交流分量幅值相同、相位相反，忽略高次谐波。

即上、下桥臂电流分别为

将式(13)、式(14)代入式(12)的第一式，可得到A相上桥臂电容总电压，如式(15)所示，且可得到推论。

基于式(15)，并运用文献[23]中的推导方法，可知：

1) 直流分量方程

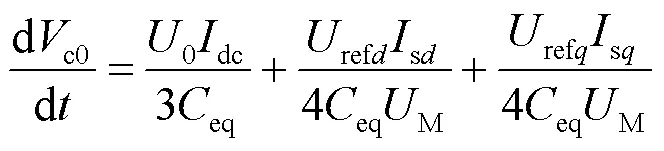
2) 基频分量方程

3) 二倍频分量方程

因此，桥臂电容总电压为

将式(13)、式(19)代入式(12)可得到推论2。

结合交流量基本方程式(6)的Park变换，得到：

根据假设2，可知：

将式(22)、式(23)代入直流基本方程式(2)，得到：

类似地，下半部分变流器直流侧电压为

式(24)、式(25)相加得到真双极MMC直流端口方程为

由式(26)可得到推论3。

推论3 真双极MMC在直流侧可进行戴维南等效，其等效电压源大小为桥臂输出电压直流分量的4倍，等效阻抗为桥臂阻抗的4/3倍。

2 LCC数学模型

在昆柳龙直流工程中，LCC由上、下两部分12脉动整流器直流侧串联和交流侧并联而成。形成±800 kV的特高压直流电压等级，简称特高压LCC。12脉动整流器结构如图2所示。

图2 12脉动整流器

设PCC点电压为

YY变压器二次侧整流器的开关函数基频分量为

YD变压器二次侧整流器的开关函数基频分量为

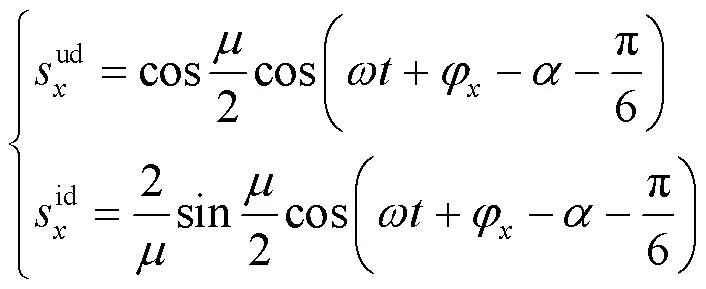
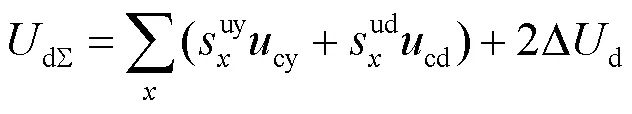
12脉动整流器的交流侧电流为

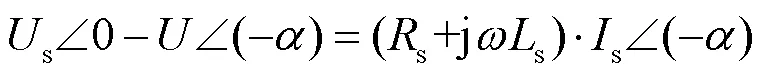
解得的PCC点电压幅值为

3 全系统电磁暂态仿真模型

3.1 昆柳龙直流工程结构

在昆柳龙直流工程中，MMC采用轴解耦控制策略，LCC采用定直流电流控制器。该部分控制模型已有完善研究，因此不再赘述。完整的输电系统结构如图3所示。

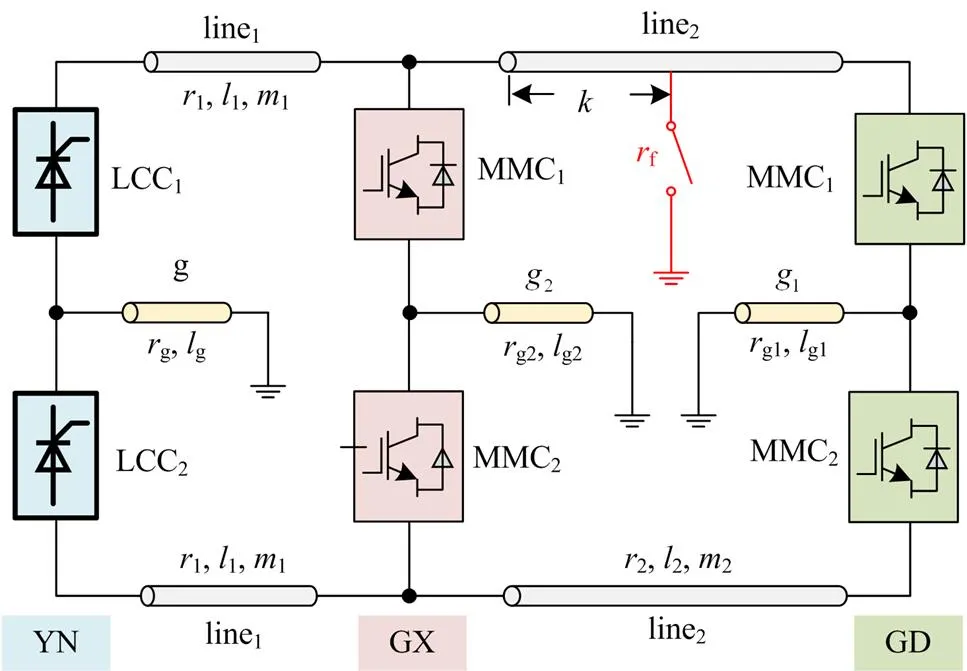
图3 昆柳龙直流工程结构

3.2 昆柳龙直流工程的等效电路

根据推论3、推论4，将换流站进行相应的戴维南等效，全系统等效电路如图4所示。其中支路Aa表示云南两个LCC整流站，Bb和bF、Dd和dH分别表示广西两个MMC换流站和广东两个MMC换流站，所有参数均在图中标出。

AB、EF、BCD、EH都是相应的直流侧互联传输线，aG、bG和dG为云南、广西和广东的接地线，C为故障点，G为参考地。图中蓝色受控源表示线路的互感电动势，它们的表达式和所涉及符号均在图中给出，s表示微分算子。

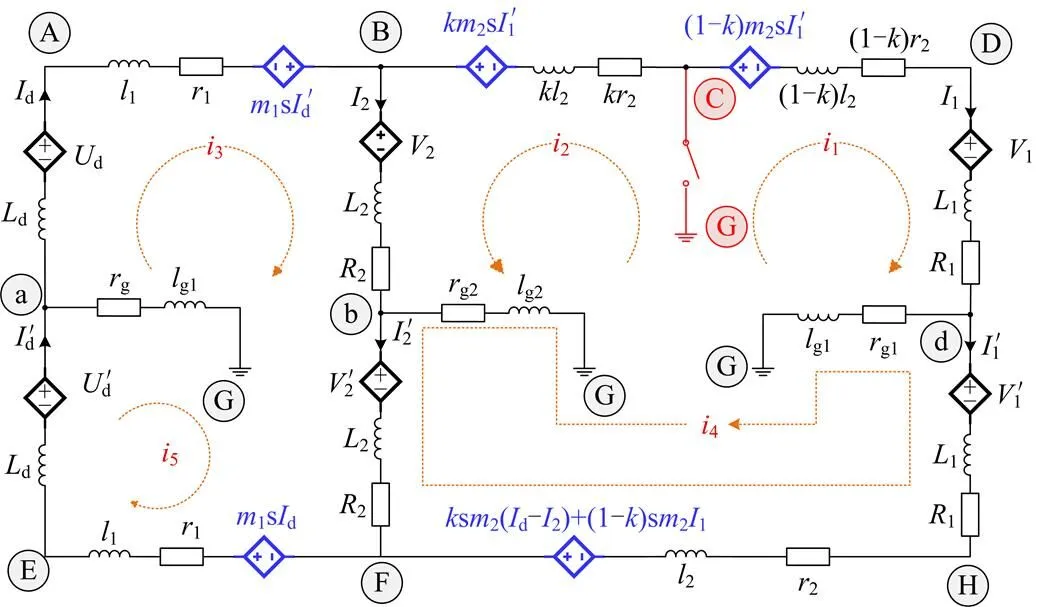
图4 昆柳龙直流工程等效电路

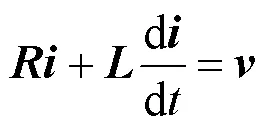
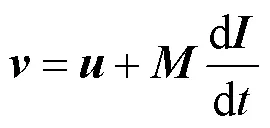
式(39)和各换流站模型、控制器模型共同构成了全系统的电磁暂态仿真模型。其中涉及到的电感矩阵、电阻矩阵、互感矩阵、网孔独立源总电压向量、变换矩阵和的表达式见附录。

4 算例验证与分析

为验证本文提出的建模方法的有效性，设计如下场景：= 5.1 s时刻，传输线line2中点处发生直流单极接地故障，即故障位置0.5。计算故障情景下电流、电压波形，并以电磁暂态软件PSCAD得到仿真结果作为参考进行比较。

图5、图6分别给出了故障下真双极HSM-MMC和LCC直流侧波形。其中本文提出模型得到的结果以红色曲线表示，PSCAD仿真的结果以蓝色曲线表示。

图5 真双极HSM-MMC直流侧波形

图6 LCC直流侧波形

由仿真结果可看出，由于计算中忽略传输线的波过程，导致波形抖动缺失，但是各电气量波形与PSCAD仿真结果整体吻合。尽管如此，计算结果基本正确，而由于对传输线集中化大大减少了计算量，利大于弊，因此所提实用模型在直流故障下可以对MTDC进行较好的工程近似。在该工程应用场景中，电磁仿真主要用于保护整定和故障分析，因此工程精度标准较宽松——主要故障电气量的极值误差不大、波形整体趋势正确即可。

5 结论

本文通过推导MTDC中真双极混合桥MMC和特高压LCC的数学模型，给出了两者在直流侧的戴维南等效电路。结合各换流站的控制系统，运用网孔分析法求解全系统等效电路，可以获得各换流站直流侧电压、电流波形，实现MTDC的电磁暂态仿真。本文建模方法的优势及相关结论如下所述。

1) 本文研究对象为南方电网建设的昆柳龙三端混合直流输电工程，是世界首个多端混合特高压直流工程。因此所研究的直流输电系统建模相关工作可直接指导直流故障保护整定，具有较高的工程实用价值。

2) 本文所提模型与昆柳龙工程详细原始PSCAD模型的仿真结果具有良好的一致性，验证了本文所提模型的有效性；同时所得到的直流故障下电气量结果可以直接指导工程实践。

3) 在直流故障场景下，LCC模型忽略交直流滤波器以及直流电气量的交流分量；传输线用有互感的RL支路等效。以上近似可以减小模型复杂度，大大减少计算量，同时计算精度满足工程要求。

昆柳龙直流工程的等效电路求解过程中，涉及的矩阵、向量：

[1] 张爽, 李宏强, 王峰, 等. 基于电压源换流器的多端柔性直流输电系统拟交流最优潮流[J]. 电力系统保护与控制, 2020, 48(13): 31-37.

ZHANG Shuang, LI Hongqiang, WANG Feng, et al.Quasi-AC optimal power flow for voltage source converter-based multi-terminal DC system[J]. Power System Protection and Control, 2020, 48(13): 31-37.

[2] RAHMAN M H, XU L, YAO L. Protection of large partitioned MTDC Networks Using DC-DC converters and circuit breakers[J]. Protection and Control of Modern Power Systems, 2016, 1(2): 170-178.

[3] 葛廷利, 宁博扬, 陈金辉. 受端多端的混合直流系统输送风电的控制策略研究[J]. 电力系统保护与控制, 2016, 44(24): 191-195.

GE Tingli, NING Boyang, CHEN Jinhui. Research on control strategy of received multiterminal DC system transporting mixed by the wind[J]. Power System Protection and Control, 2016, 44(24): 191-195.

[4] 凌卫家, 孙维真, 张静, 等. 舟山多端柔性直流输电示范工程典型运行方式分析[J]. 电网技术, 2016, 40(6): 1751-1758.

LING Weijia, SUN Weizhen, ZHANG Jing, et al. Analysis of typical operating modes of Zhoushan multi-terminal VSC-HVDC pilot project[J]. Power System Technology, 2016, 40(6): 1751-1758.

[5] 饶宏, 洪潮, 周保荣, 等. 乌东德特高压多端直流工程受端采用柔性直流对多直流集中馈入问题的改善作用研究[J]. 南方电网技术, 2017, 11(3): 1-5.

RAO Hong, HONG Chao, ZHOU Baorong, et al. Study on improvement of VSC-HVDC at inverter side of Wudongde multi-terminal UHVDC for the problem of centralized multi-infeed HVDC[J]. Southern Power System Technology, 2017, 11(3): 1-5.

[6] 倪晓军, 赵成勇, 郭春义, 等. 混合双馈入直流输电系统中LCC-HVDC对VSC-HVDC系统强度的影响[J].电网技术, 2017, 41(8): 2436-2442.

NI Xiaojun, ZHAO Chengyong, GUO Chunyi, et al. Effects of LCC-HVDC on system strength of VSC-HVDC in hybrid dual-infeed HVDC system[J]. Power System Technology, 2017, 41(8): 2436-2442.

[7] NI X, GOLE A M, ZHAO C, et al. An improved measure of AC system strength for performance analysis of multi-infeed HVDC systems including VSC and LCC converters[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 169-178.

[8] DARYABAK M, FILIZADEH S, VANDAEI A B. Dynamic phasor modeling of LCC-HVDC systems: unbalanced operation and commutation failure[J]. Canadian Journal of Electrical and Computer Engineering, 2019, 42(2): 121-131.

[9] 朱艺颖, 于钊, 李柏青, 等. 大规模交直流电网电磁暂态数模混合仿真平台构建及验证(一)整体构架及大规模交直流电网仿真验证[J]. 电力系统自动化, 2018, 42(15): 164-170.

ZHU Yiying, YU Zhao, LI Baiqing, et al. Construction and validation of electromagnetic transient digital-analog hybrid simulation platform for large-scale AC/DC power grids: part one general configuration and simulation validation of large scale AC/DC power grids[J]. Automation of Electric Power Systems, 2018, 42(15): 164-170.

[10] 徐政, 蔡晔, 刘国平. 大规模交直流电力系统仿真计算的相关问题[J]. 电力系统自动化, 2002, 26(15): 4-8.

XU Zheng, CAI Ye, LIU Guoping. Some problems in the simulation of large-scale AC/DC power systems[J]. Automation of Electric Power Systems, 2002, 26(15): 4-8.

[11] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.

[12] 王思华, 赵磊, 王军军, 等. 基于MMC的直流输电系统双极短路故障保护策略研究[J]. 电力系统保护与控制, 2021, 49(11): 9-17.

WANG Sihua, ZHAO Lei, WANG Junjun, et al. Research on protection strategy of a bipolar short circuit fault in an HVDC transmission system based on MMC[J]. Power System Protection and Control, 2021, 49(11): 9-17.

[13] MIYAKE M, OHASHI A, YOKOMICHI M, et al. A consistently potential distribution oriented compact IGBT model[C] // IEEE Power Electronics Specialists Conference, June 15-19, 2008, Rhodes, Greece: 998-1003.

[14] LESNICAR A, MARQUARDT R. An innovative modular multilevel converter topology suitable for a wide power range[C] // IEEE Bologna Power Tech Conference Proceedings, June 23-26, 2003, Bologna, Italy.

[15] GNANARATHNA U N, GOLE A M, JAYASINGHE R P. Efficient modeling of modular multilevel HVDC converters (MMC) on electromagnetic transient simulation programs[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 316-324.

[16] 喻悦箫, 刘天琪, 王顺亮, 等. 基于平均值模型的双端MMC-HVDC系统小信号建模[J]. 中国电机工程学报, 2018, 38(10): 2999-3006, 3150.

YU Yuexiao, LIU Tianqi, WANG Shunliang, et al. Small signal modeling of two-terminal MMC-HVDC based on AVM model[J]. Proceedings of the CSEE, 2018, 38(10): 2999-3006, 3150.

[17] 曹帅, 向往, 林卫星, 等. 含风电的真双极混合型MMC-MTDC系统故障穿越及能量耗散控制[J]. 电力系统保护与控制, 2019, 47(7): 39-48.

CAO Shuai, XIANG Wang, LIN Weixing, et al. Fault ride-through and energy dissipation control of bipolar hybrid MMC-MTDC integrating wind farms[J]. Power System Protection and Control, 2019, 47(7): 39-48.

[18] 孔明, 汤广福, 贺之渊. 子模块混合型MMC-HVDC 直流故障穿越控制策略[J]. 中国电机工程学报, 2014, 34(30): 5343-5351.

KONG Ming, TANG Guangfu, HE Zhiyuan. A DC fault ride-through strategy for cell-hybrid modular multilevel converter based HVDC transmission systems[J]. Proceedings of the CSEE, 2014, 34(30): 5343-5351.

[19] CHEN J, LI B, BO D, et al. Simulation and analysis of fault characteristics of the MMC-HVDC system under bipolar connection mode[C] // IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), October 25-28, 2016, Xi'an, China: 2534-2538.

[20] HUI D, WU Y, YI Z, et al. System stability analysis of Xiamen bipolar MMC-HVDC project[C] // 12th IET International Conference on AC and DC Power Transmission (ACDC 2016), May 28-29, 2016, Beijing, China: 1-6.

[21] 程成, 孙建军, 宫金武, 等. 基于Bergeron等值线路的机电电磁混合仿真接口模型[J]. 电网技术, 2019, 43(11): 198-203.

CHENG Cheng, SUN Jianjun, GONG Jinwu, et al. An interface model of electromechanical and electromagnetic hybrid simulation based on equivalent circuit of Bergeron line[J]. Power System Technology, 2019, 43(11): 198-203.

[22] WANG Q, BO Z, MA X, et al. Integrated protection based on multifrequency domain information for UHV half-wavelength AC transmission line[J]. Protection and Control of Modern Power Systems, 2016, 1(2): 157-163.

[23] 李正. MMC-HVDC建模, 控制和小信号稳定性分析[D]. 济南: 山东大学, 2019.

LI Zheng. Modelling, control and small-signal stability analysis of MMC-HVDC[D]. Jinan: Shandong University, 2019.

A practical model suitable for DC fault simulation of a multi terminal DC transmission system

ZHENG Wei1, GUO Jianbao1, YANG Guangyuan1, CAO Runbin2, NIE Shaoxiong2, LI Guiyuan2

(1. Maintenance and Test Center of Extra-high Voltage Transmission Company, China Southern Power Grid Co., Ltd., Guangzhou 510080, China; 2. China Southern Power Grid Electric Power Research Institute Co., Ltd., Guangzhou 510080, China)

Multi terminal DC (MTDC) has become a competitive cross-regional high-power transmission technology, but there has been little research on its complete mathematical model because of its structural complexity. A true bipolar hybrid bridge modular multi-level converter (MMC) is an important part of ultra-high voltage MTDC. If its mathematical model still adopts the simple half-bridge MMC, electrical connection on the AC side of the true bipolar MMC cannot be reflected. Also, the rationality of extending the 0-1 binary switching function of the half-bridge MMC model to the hybrid bridge has yet to be proven. To solve the above-mentioned problems in MTDC modeling, Kun-Liu-Long DC project is taken as an example. First, the complete mathematical model of the true bipolar hybrid bridge MMC is deduced, and the quasi-steady state and lumped parameter approximation of conventional HVDC converter stations and DC transmission lines are carried out. Then, both accuracy and complexity are considered to establish a practical engineering model of MTDC under a DC fault. Finally, the DC unipolar ground fault is calculated and analyzed using the proposed model. Compared with the calculation results of PSACD, the validity of the proposed model is verified.

MTDC; MMC; true bipolar hybrid bridge; electromagnetic transient simulation; Kun-Liu-Long DC project

10.19783/j.cnki.pspc.211031

2021-08-05；

2021-09-24

郑 伟(1985—)，男，硕士，高级工程师，从事直流输电技术研究；E-mail: 415340558@qq.com

国建宝(1981—)，男，硕士，高级工程师，从事直流控制保护技术研究；E-mail: gjb104@163.com

聂少雄(1991—)，男，硕士，工程师，从事直流控制保护技术研究。E-mail: nsxboy@qq.com

This work is supported by the Science and Technology Project of China Southern Power Grid Co., Ltd. (No. ZBKJXM20180635).

南方电网科技项目资助“柔性直流控保系统与阀控系统之间的保护配合及控制协调优化研究”(ZBKJXM20180635)

(编辑 姜新丽)