考虑天然来水随机性的水火电系统机组检修计划
2022-06-16田年杰姜有泉郑志佳刘明波
代 江,田年杰,姜有泉,郑志佳,刘明波,谢 敏
考虑天然来水随机性的水火电系统机组检修计划
代 江1,田年杰1,姜有泉1,郑志佳2,刘明波2,谢 敏2
(1.贵州电网有限责任公司电力调度控制中心,贵州 贵阳 550000;2.华南理工大学电力学院,广东 广州 510640)
如何合理安排机组检修是水火电系统调度运行中的一项重要任务。在长时间尺度下,天然来水的随机性使机组检修计划本质上成为随机优化问题,通常采用场景法描述随机性,但其形成的高维优化问题难以直接求解。建立多场景耦合的水火电系统机组检修优化模型,利用多学科协同优化(Multidisciplinary Collaborative Optimization, MCO)方法将各场景间的非预期性约束及检修变量耦合约束解耦,实现了原问题的降维,且MCO结构具有内在的并行性。此外,在基于MCO的系统级优化问题中,用绝对值惩罚项替代二次惩罚项,保证该问题是一个混合整数线性规划问题,有利于提高计算效率。最后以某省级实际水火电系统为算例进行仿真分析,验证了所提模型和算法的有效性。
水火电系统;机组检修计划;场景法;非预期性约束;多学科协同优化
0 引言
为了保证水火电系统中发电机组运行的可靠性,充分发挥水火电互补能够降低发电成本、减少环境污染的特点,发电机组需要进行充分必要的检修。目前,我国主要的检修机制是预防性检修,即在满足系统运行和机组特性等约束条件的前提下,确定一定调度周期内机组停机进行检修的时间[1-3]。为了提高水电资源的利用率,水火电系统中梯级水电站投入生产运营的规模也在日益增大。由于梯级水电站群上下游水库间存在复杂的水力耦合关系,某一台机组是否安排检修将影响到本级水库及上下游水库的调度决策[4]。因此,针对含有梯级水电的系统合理地安排机组检修计划十分重要,已有学者进行了相关的研究。文献[5]将水库类比为能源储备,以最大化调度周期末各水库的水量及最小化火电运行成本为目标,采用差分进化算法对梯级水电站的机组检修计划进行优化。文献[6]重点考虑了梯级水电站群上下游的耦合关系,建立了梯级水电站的中长期调度和检修计划双层优化模型,根据径流的预测量进行决策,最终达到梯级水电站检修计划对运营收益影响最小的效果。文献[7]以最大化水电站净收益为目标,建立了梯级水电系统机组检修计划优化的混合整数线性规划(Mixed Integer Linear Programming, MILP)模型。
天然来水对梯级水电站运行调度的影响十分明显,文献[5-7]均将天然来水作为确定量进行研究,然而在长期时间尺度下难以保证天然来水的预测精度[8],因此水火电系统中检修计划的制定问题本质上具有随机性质。基于场景法的思想处理随机性在研究中得到了广泛应用[9-11],场景法假定随机量的预测误差服从某一概率分布,通过抽样生成多个误差场景来模拟随机性,将随机模型转化为确定性模型进行求解。显然,误差场景越多,对随机性的描述越准确,但过多的场景也会带来计算问题。文献[12]基于场景法考虑天然来水的随机性,对于某实际系统,生成五个场景实现梯级水电站检修计划与中长期调度的协同优化。然而,随着场景数的增加,变量和约束的数量激增,直接求解存在困难。场景缩减技术(如中心点聚类法、自组织映射聚类法等)可以精简场景数目,降低求解难度[13-14],文献[15]将聚类与优化算法结合用于缩减可再生能源出力场景,文献[16]针对梯级水电检修问题,分别应用三种场景缩减技术,指出场景缩减技术的选择对求解结果有很大影响。对多场景问题进行解耦可以降低求解难度,文献[17]运用异步块迭代法对多场景的高维线性修正方程组进行解耦,降低了存储需求。文献[18]在求解含风电接入的电力系统随机动态经济调度问题时,采用多学科协同优化(Multidisciplinary Collaborative Optimization, MCO)方法对场景进行解耦,提高了场景法处理问题随机性的效率。近年来,部分文献在对随机优化问题的研究中讨论了非预期性约束的重要性[19-20],该约束表现为:当前决策变量的确定不应受到还未被观测到的随机性的影响。目前,在水火电系统的相关研究中,对非预期性约束的考虑还不多见。而在有限个场景的情况下,考虑非预期性约束的问题可以被分解为多个相互之间仅有非预期性约束耦合的子问题[21],在算法中如何利用这一特点是关键。
本文考虑水电站天然来水的随机性,在满足整个系统、机组、水库及输电线路等特性和约束条件的前提下,以最小化火电运行费用及水电站弃水成本之和为目标,建立了水火电系统机组检修计划的多场景优化模型。采用MCO方法,将预测场景优化问题设置为系统级问题,将误差场景优化问题设置为子学科级问题,通过系统级问题与子学科级问题间的信息传递,实现各场景间的非预期性及检修变量耦合约束的解耦,避免直接求解高维的原问题,并利用MCO结构特点实现了误差场景优化问题的并行求解。同时,本文对系统级与子学科级的模型形式进行了改进,既保证了系统级优化问题存在可行域,又巧妙地使各场景对应的问题为MILP形式,更易求解。最后,在某省级梯级水火电系统上进行了仿真分析。
1 水火电机组检修随机优化模型
1.1 目标
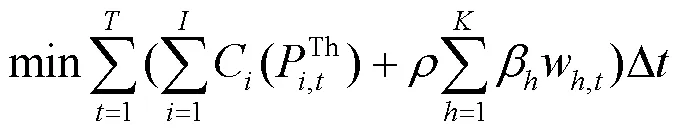
1.2 约束条件
约束条件包括对系统、水火电机组及水库的运行调度限制及检修任务的约束,分别描述如下。
1) 功率平衡约束
整个系统的功率平衡约束可描述为

2) 线路传输容量约束
输电线路传输的功率不应超过线路传输容量的上下限,即


3) 机组出力约束

4) 备用约束
通过预留足够的系统旋转备用容量可以应对负荷预测误差带来的影响,因此,添加旋转备用约束可以保证系统运行的可靠性。

5) 水电站运行限制
水电站的运行调度需要在保证安全的前提下进行,包括如下约束。

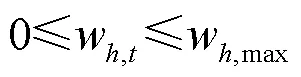


6) 梯级水电站上下游水量耦合约束
上下游水库之间构成的水力耦合网络是梯级水电站一个重要的特点。本文以天为时间单位进行优化,忽略水流滞时的影响,对梯级水电站上下游水量的耦合约束描述为

7) 水电站出力约束
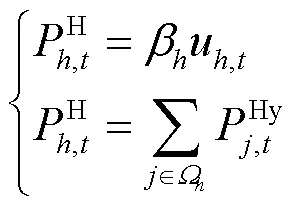
8) 机组检修时长约束
机组在调度周期内必须完成规定时长的检修任务。

9) 机组检修连续性约束
机组开始检修后不能中断检修任务,即机组检修具有连续性。

1.3 随机优化模型的紧凑形式

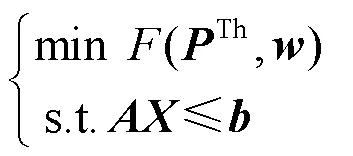

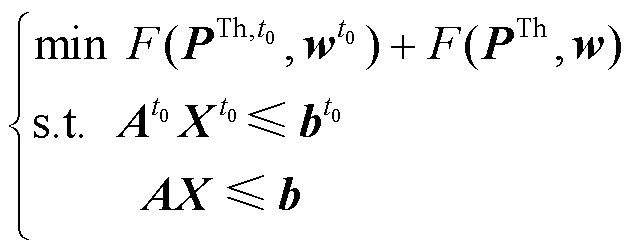
2 水火电机组检修多场景优化模型



为了求解式(14)所示的模型,利用预测场景与随机抽样生成的个误差场景描述天然来水的随机性。需要注意的是,预测场景与各个误差场景之间并非相互独立,而是存在非预期性约束这一耦合关系。非预期性约束的含义是:当考虑随机因素时,每次针对当前情况进行的决策不应该受到未来随机因素的影响,这也就意味着不同的场景应当具有相同的起点。制定检修计划时,在12月31日的决策应该先于随机变量的发生而制定,不受到第二年随机来水的影响。各个场景之间的非预期性约束如图1所示。
基于采样平均近似法的思想,抽样生成的每个场景发生的概率相等,于是将随机规划模型转化为确定性模型,即

式(15)所示的确定性模型通过对预测场景及误差场景进行集中式求解,可以优化得到一个适应天然来水随机性的检修方案,此为传统场景法的做法。通常情况下,抽取的场景数越多,对随机性的描述越准确,然而随着场景数增多,问题的变量和约束数量也急剧增长,导致问题维数增加,甚至可能出现无法求解的情况。
3 基于多学科协同优化的求解方法
为了解决传统场景法带来的高维数问题,本文基于MCO方法将各个场景解耦,通过系统级与子学科级优化问题之间的信息传递协同各个场景间的耦合变量,最终迭代得到一个适用于各个场景的检修计划。
3.1 多学科协同优化方法
MCO是一种二级多学科优化算法,其核心思想是将复杂的优化问题按某一标准分解为系统级优化问题和子学科级优化问题[23-24]。MCO方法的流程为:首先给出一个设计变量,子学科级问题在优化时向给出的设计变量逼近,并将求解结果返回系统级问题,其中各子学科之间相互独立。而系统级优化问题负责缩小各子学科级问题之间的信息差,并向所有的子学科传递新的设计变量。两级问题在多次迭代中逐步协同,直至收敛输出结果。
3.2 场景解耦
3.2.1场景耦合约束
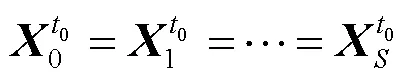
此时,各场景在时刻的耦合约束如图2所示。图2中绿框表示在时刻水、火电机组的出力与水电站的弃水量作为独立变量影响其他三组变量,因此在各场景中,只需使上述时刻时的独立变量相等,即可满足非预期性约束。
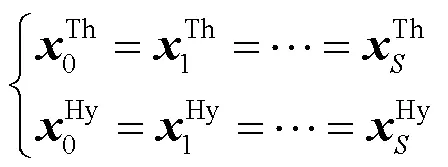

3.2.2基于场景解耦的检修优化模型
1) 系统级优化问题


2) 子学科级优化问题
每个误差场景都被设置为子学科级优化问题,在优化中向系统级问题传递的设计变量逼近。

如式(18)和式(19)所示,利用MCO算法,场景间耦合约束在系统级优化问题中以一致性约束的形式出现,在子学科级优化问题中以惩罚项的形式出现。高维的原问题被分解为多个低维的优化问题,通过两级问题的相互迭代,最终能够得到满足耦合约束的解。
3.2.3采用绝对值惩罚项替代二次惩罚项





如上所示,系统级优化问题中不再出现二次项。采用同样的方式对子学科级优化问题进行线性化,最终使整个模型始终保持为MILP形式。
3.2.4收敛条件
传统的MCO模型中,收敛条件是相邻两次迭代中系统级目标函数值的变化率不超过某一微小值。本文模型优化的目的是获得覆盖天然来水预测及误差场景的检修计划;同时各个场景在决策时刻变量的值应满足非预期性约束。为此,利用3.2.3节中引入的连续变量设计收敛判据,如式(23)与式(24)。
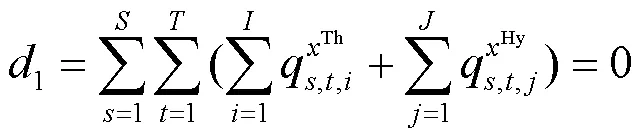

3.3 算法流程
本文采用MCO方法将各个场景解耦,由误差场景形成的子学科级问题相互独立,能够实现并行计算。基于多学科协同优化的机组检修优化流程如图3所示。
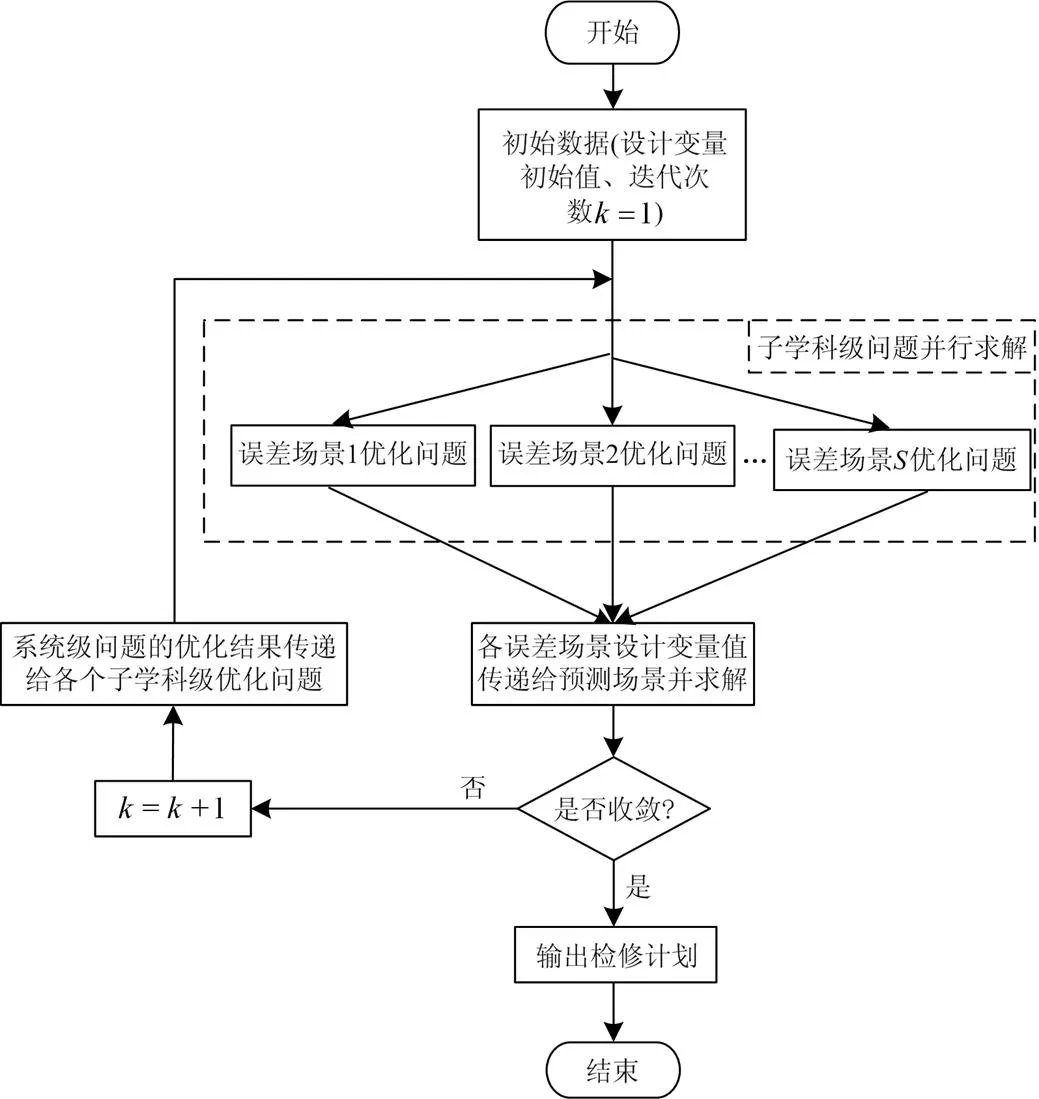
图3 基于多学科协同优化的机组检修优化流程图
4 算例分析
本节以某省级实际水火电系统为算例进行仿真计算。该系统包含1 348个节点、1 721条支路、火电厂21座、水电站23座。其中火电厂共包含65台火电机组,水电站共包含90台水电机组,拟安排检修任务的有62台火电机组和77台水电机组。该省级电力系统全年统调负荷如图4所示。系统中共有3个梯级流域,其中水电站的梯级耦合关系如图5所示。
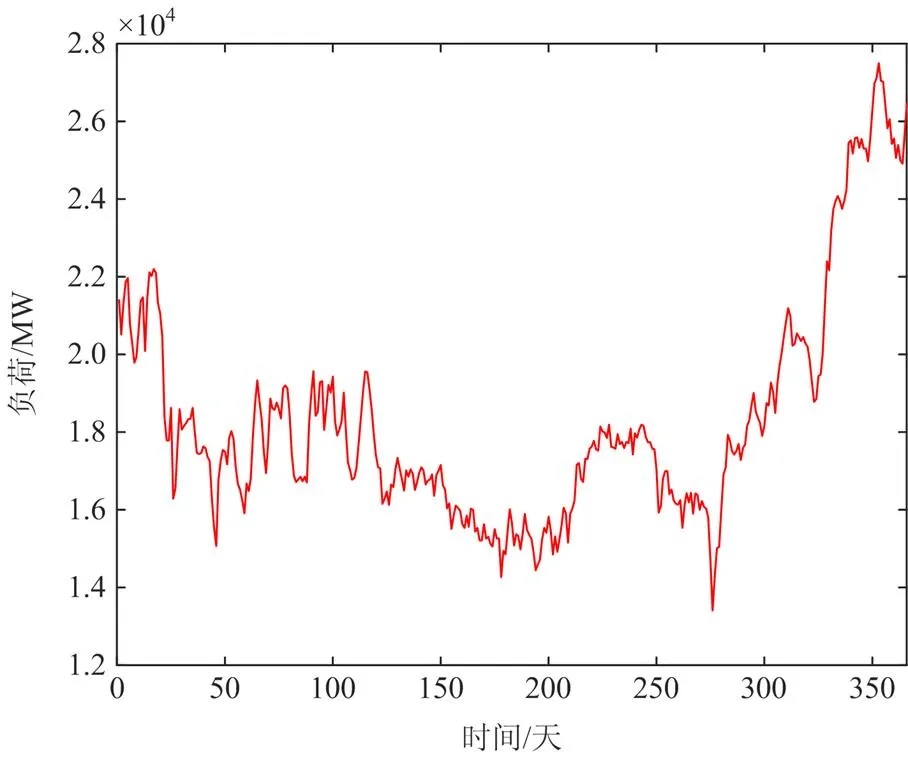
图4 某省级系统年负荷曲线

图5 3个流域中水电站的梯级耦合关系
采用各水电站所在地天然来水的历史数据生成预测场景,误差场景的生成采用两种方法:1) 所有水电站的天然来水分别取预测量的0.8倍、0.9倍和1.2倍生成3个误差场景;2) 假设天然来水的预测误差服从正态分布,设置均值为预测值,标准差设定为0.2个,通过随机抽样产生100个误差场景;由此产生3个误差场景与100个误差场景两个算例。采用GAMS (General Algebraic Modeling System) 软件中的网格工具实现本文基于多学科协同优化的机组检修计划(MCO-GMS)模型的并行计算,并与采用GAMS中的Gurobi求解器直接求解多场景耦合模型对比,优化结果如表1。
表1中第1列与第2列分别是采用多场景耦合模型与MCO-GMS模型求解得到的优化结果,其具体物理含义为:在优化得到的检修计划下,所有场景火电机组运行成本与水电站弃水成本之和的期望值,称为期望总成本,第3列是两种模型期望总成本的相对误差。设置3个误差场景时,采用本文方法进行求解,其优化结果与求解多场景耦合模型获得的结果仅有0.0021%的相对误差。当误差场景增加到100个时,高维的结构导致多场景耦合模型求解时超出内存,无法求解。而本文模型将原问题分解为多个低维的问题,有效地化解了原问题求解的难点。并且本文方法在求解时间上有明显的优势,表2为直接求解多场景耦合模型与并行求解本文模型所用的时间,为了体现本文方法可并行计算的优势,同时对本文模型进行串行求解。

表1 多场景耦合模型与MCO-GMS模型期望总成本对比

表2 三种模式计算时间的比较
从表2中可以看到,利用本文方法的求解时间远小于传统场景法直接求解所需的时间。同时,本文方法具有的可并行计算结构能够进一步加速问题的求解,在3个误差场景的情况下,并行计算用时为串行计算的62.62%,在100个误差场景的情况下,这一比例进一步降低为57.97%,随着场景数的增加,并行计算的加速效果更明显。
为避免系统级优化问题中一致性约束导致的不可行问题,通常将一致性约束以二次惩罚项的形式增广到目标函数中[25],本文采用绝对值惩罚项代替二次惩罚项,并且利用一组连续变量与对应的两组约束将其线性化,避免问题变为较难求解的混合整数二次规划形式。在其他条件相同的情况下,惩罚项不同时的求解结果对比如表3所示。同时,在不同惩罚项形式下,3个误差场景与100个误差场景算例中收敛判据1和2的趋势如图6和图7所示。
表3中在二次惩罚项和绝对值惩罚项两种情况下,MCO-GMS模型求出的总成本期望值一致,但绝对值惩罚项在线性化后,由于问题保持为MILP形式,求解时间大大减少:在3个误差场景的情况下,两者迭代的次数相同,但线性化后计算时间为未线性化时的77.96%;在100个误差场景的情况下,线性化后问题在求解时多迭代了一次,但计算时间仅为未线性化时的72.25%。线性化对问题求解的加速效果明显。
表4展示了3个误差场景与100个误差场景两个算例在优化后的火电机组期望运行成本、水电机组期望站成本与期望总成本。可以看出,100个误差场景算例优化后的期望总成本更小,这与算例的设置有关,3个误差场景算例中,天然来水分别设置为0.8、0.9、1.2倍预测场景的天然来水;而100个误差场景算例中,天然来水服从以预测值为均值、标准差为0.2的正态分布;因此3个误差场景算例中天然来水的期望值要更小。由于模型中水电机组的出力与发电流量成正比关系,天然来水越少,水电站能够补充的水量就越少,水电机组的最大发电量也随之减少,为了满足功率平衡约束,火电机组需要发更多的电量,从而增加了运行成本的期望值,此时虽然期望弃水成本有所减少,但最终的期望总成本是增加的。

表3 不同惩罚项对计算时间与迭代次数的影响
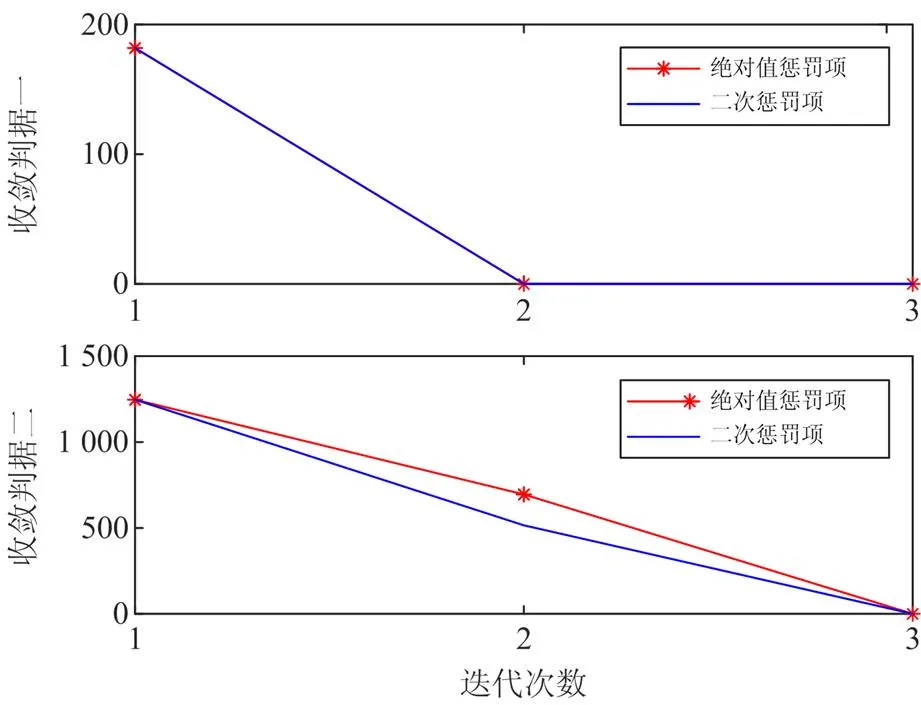
图6 3个误差场景算例中和的变化情况

图7 100个误差场景算例中和的变化情况

表4 MCO-GMS模型优化后的目标值
最后,以100个误差场景的求解结果为例绘出了部分水火电机组的检修计划安排,采用深色块表示机组的检修状态,如图8和图9所示。图中,水火电机组的检修计划整体上呈“错峰”特点:由于目标函数中对弃水量的考虑,水电机组倾向于在来水较为丰富的丰水期(约为每年的第150至第270天)以外进行检修,火电机组为支持水电机组多发电,大部分在丰水期附近执行检修任务,体现了水火电系统互补的特点。

图8 部分火电机组检修计划
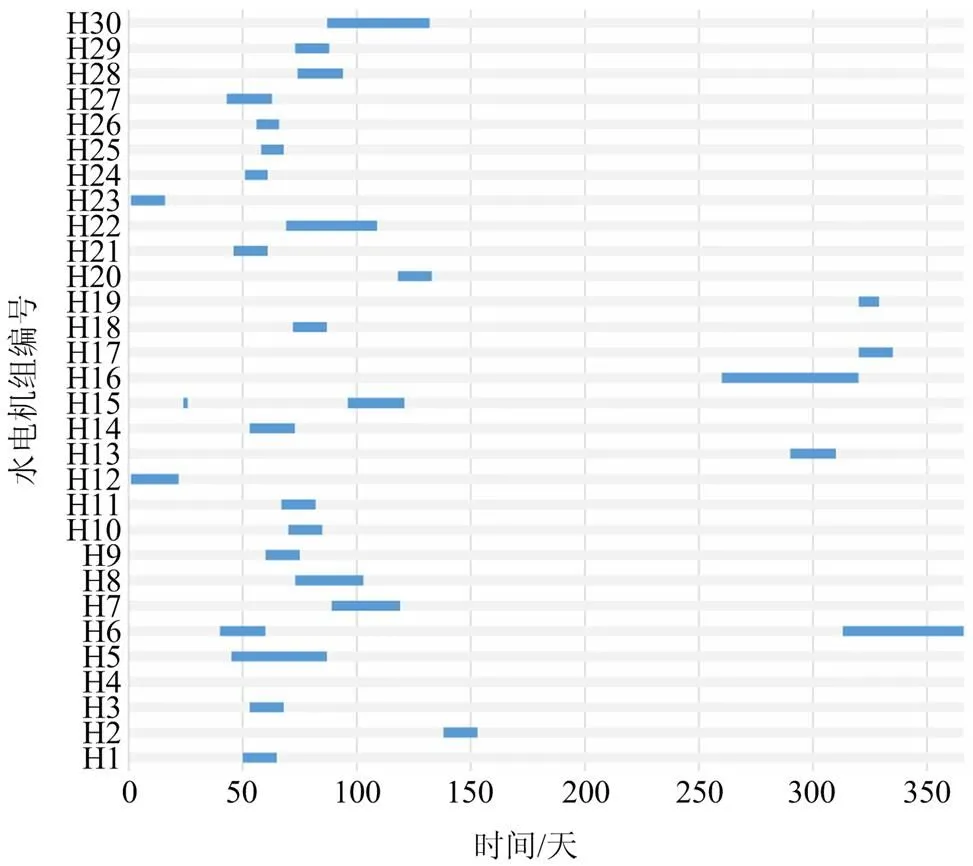
图9 部分水电机组检修计划
5 结论
本文考虑天然来水的随机性,基于场景法构建了水火电系统机组检修计划优化模型,采用MCO方法有效求解多场景下具有高维性质的原问题,并利用并行计算、线性化等技术加速问题的求解,实现了随机天然来水情况下机组检修计划的优化。
某省级实际水火电系统进行仿真分析的结果表明,本文所建立的机组检修计划优化模型能够合理地安排水火电机组的检修计划,所提方法能够有效处理多场景问题的高维性质,在降低计算难度和提高计算效率两个方面均有明显改善,适用于求解场景法处理随机性的高维优化问题。
[1] 谢冰. 机组检修计划及发电计划优化问题研究[D]. 杭州: 浙江大学, 2018.
XIE Bing. Research on unit maintenance scheduling and power generation scheduling optimization[D]. Hangzhou: Zhejiang University, 2018.
[2] 许丹, 罗治强, 李旻, 等. 考虑安全约束及电量执行的年度发电与检修联合优化模型[J]. 电力系统保护与控制, 2019, 47(17): 133-139.
XU Dan, LUO Zhiqiang, LI Min, et al. A combined optimization model for annual generation and maintenance scheduling considering safety constraints and power execution[J]. Power System Protection and Control, 2019, 47(17): 133-139.
[3] 徐波, 孙宏斌, 鲁刚, 等. 基于机会维修的热电联产机组检修计划[J]. 电力建设, 2018, 19(12): 95-101.
XU Bo, SUN Hongbin, LU Gang, et al. Maintenance optimization based on oppotunistic maintenance for combined heat and power unit[J]. Elcetric Power Construction, 2018, 19(12): 95-101.
[4] 郭有安, 管镇. 澜沧江梯级水电站发电与机组检修联合优化研究[J]. 水力发电, 2017, 43(10): 83-86.
GUO Youan, GUAN Zhen. Research on joint optimization of power generation and unit overhaul for the cascade hydropower stations in Lancang River[J]. Water Power, 2017, 43(10): 83-86.
[5] GUEDES L S M, VIEIRA D A G, LISBOA A C, et al. A continuous compact model for cascaded hydro-power generation and preventive maintenance scheduling[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 702-710.
[6] 刘方, 张粒子, 蒋燕, 等. 电力市场环境下梯级水电站中长期调度与检修计划双层优化模型[J]. 电网技术, 2018, 42(5): 1541-1549.
LIU Fang, ZHANG Lizi, JIANG Yan, et al. Bi-level optimal model of mid-long term scheduling and maintenance planning for cascade hydropower stations in electricity market environment[J]. Power System Technology, 2018, 42(5): 1541-1549.
[7] RODRÍGUEZ J A, ANJOS M F, CÔTÉ P, et al. MILP formulations for generator maintenance scheduling in hydropower systems[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6171-6180.
[8] XU Bin, ZHONG Pingan, ZAMBON R C, et al. Scenario tree reduction in stochastic programming with recourse for hydropower operations[J]. Water Resources Research, 2015, 51(8): 6359-6380.
[9] XU Jian, YI Xiankun, SUN Yuanzhang, et al. Stochastic optimal scheduling based on scenario analysis for wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1548-1559.
[10] 杨明, 罗隆福. 计及风电与负荷不确定性的电力系统无功随机优化调度[J]. 电力系统保护与控制, 2020, 48(19): 134-141.
YANG Ming, LUO Longfu. Stochastic optimal reactive power dispatch in a power system considering wind power and load uncertainty[J]. Power System Protection and Control, 2020, 48(19): 134-141.
[11]都嘉慧, 王长江, 李凌, 等. 计及换流器损耗的风电经柔直并网系统的随机最优潮流模型[J]. 中国电力, 2020, 53(5): 77-88.
DU Jiahui, WANG Changjiang, LI Ling, et al. Stochastic optimal power flow of wind turbine through flexible grid connected system considering converter coss[J]. Electric Power, 2020, 53(5): 77-88.
[12] MARTÍNEZ M V R, ZULUAGA A H E, GUIMARES F G. A MILP model for generation maintenance scheduling coordinated with hydrothermal dispatch[J]. Energy Systems, 2020, 11(1): 839-857.
[13] 徐悦, 孙建军, 丁凯, 等. 基于场景构建的电压暂降特征量随机评估方法[J]. 电力系统保护与控制, 2021, 49(9): 105-112.
XU Yue, SUN Jianjun, DING Kai, et al. Random evaluation method of voltage sag characteristics based on scenario construction[J]. Power System Protection and Control, 2021, 49(9): 105-112.
[14] GAO Yajing, XUE Fushen, YANG Wenhai, et al. Optimal operation modes of photovoltaic-battery energy storage system based power plants considering typical scenarios[J]. Protection and Control of Modern Power Systems, 2017, 2(4): 397-406.
[15]白斌, 韩明亮, 林江, 等. 含风电和光伏的可再生能源场景削减方法[J]. 电力系统保护与控制, 2021, 49(15): 141-149.
BAI Bin, HAN Mingliang, LIN Jiang, et al. Scenario reduction method of renewable energy including wind power and photovoltaic[J]. Power System Protection and Control, 2021, 49(15): 141-149.
[16] LARSEN C T, DOORMAN G L, MO B. Evaluation of scenario reduction methods for stochastic inflow in hydro scheduling models[C] // 2015 IEEE Eindhoven PowerTech, June 29-July 2, 2015, Eindhoven, Netherlands: 1-6.
[17]赵维兴, 付一木, 刘强, 等. 径流式小水电群随机环境经济调度方法[J]. 电力系统保护与控制, 2016, 44(24): 97-104.
ZHAO Weixing, FU Yimu, LIU Qiang, et al. Method for stochasticeconomic emission dispatch problem considering runoff small hydropower group[J]. Power System Protection and Control, 2016, 44(24): 97-104.
[18] XIE Min, LUO Wenhao, CHENG Peijun, et al. Multidisciplinary collaborative optimisation-based scenarios decoupling dynamic economic dispatch with wind power[J]. IET Renewable Power Generation, 2018, 12(6): 727-734.
[19] 丁涛, 李澄, 胡源, 等. 考虑非预期条件的电力系统多阶段随机规划建模理论与方法[J]. 电网技术, 2017, 41(11): 173-180.
DING Tao, LI Cheng, HU Yuan, et al. Multi-stage stochastic programming for power system planning considering nonanticipative constraints[J]. Power System Technology, 2017, 41(11): 173-180.
[20] ZHAI Qiaozhu, LI Xuan, LEI Xiaohong, et al. Transmission constrained UC with wind power: an all-scenario-feasible MILP formulation with strong nonanticipativity[J]. IEEE Transactions on Power Systems, 2017, 32(3): 1805-1817.
[21] BIRGE J R, LOUVEAUX F. Introduction to stochastic programming[M]. New York: Springer, 2011: 118-122.
[22] 陈鸿琳, 刘明波. 交流潮流约束机组组合的部分代理割方法[J]. 中国电机工程学报, 2018, 38(9): 2540-2550, 2822.
CHEN Honglin, LIU Mingbo. Partial surrogate cuts approach for alternating current power flow constrained unit commitment[J]. Proceedings of the CSEE, 2018, 38(9): 2540-2550, 2822.
[23] 周奇, 蒋平, 许辉, 等. 基于动态罚因子的多学科协同优化算法及其在船舶设计中的应用[J]. 船舶力学, 2016, 20(10): 1269-1280.
ZHOU Qi, JIANG Ping, XU Hui, et al. Application of improved multi-discipline collaborative optimization in ship conceptual design based on dynamic penalty factors[J]. Journal of Ship Mechanics, 2016, 20(10): 1269-1280.
[24]陈荃, 吴科成, 曲毅, 等. 基于多学科协同理论的可再生能源消纳责任权重测算方法[J]. 电力建设, 2021, 42(1): 49-58.
CHEN Quan, WU Kecheng, QU Yi, et al. Research on optimal weight index calculation for renewable energy applying multidisciplinary collaborative optimization theory[J]. Electric Power Construction, 2021, 42(1): 49-58.
[25]柳明星, 张伟, 张恒, 等. 基于动态罚函数的火星探测器多学科协同优化[J]. 深空探测学报, 2017, 4(3): 276-280.
LIU Mingxing, ZHANG Wei, ZHANG Heng, et al. Multidisciplinary collaborative optimization of Mars probe based on dynamic penalty function[J]. Journal of Deep Space Exploration, 2017, 4(3): 276-280.
Generator maintenance schedule of hydro-thermal power systems considering randomness of natural water inflow
DAI Jiang1, TIAN Nianjie1, JIANG Youquan1, ZHENG Zhijia2, LIU Mingbo2, XIE Min2
(1. Electric Power Dispatching and Control Center of Guizhou Power Grid Co., Ltd., Guiyang 550000, China; 2. School of Electric Power Engineering, South China University of Technology, Guangzhou 510640, China)
How to rationally arrange maintenance of generators is an important task in the dispatch and operation of hydro-thermal power systems. On a long timescale, the randomness of natural water inflow makes the generator maintenance schedule (GMS) essentially a stochastic optimization problem. The scenario-based method is usually used to describe the randomness, but it is difficult to solve efficiently the high-dimensional optimization problem with this method. This paper establishes a coupled multi-scenario GMS model of hydro-thermal power systems, applies a multi-disciplinary collaborative optimization (MCO) method to decouple the nonanticipative and the coupling constraints on maintenance variables between scenarios. Thus, the dimension of the multi-scenario GMS model is reduced and the MCO-based structure has inherent parallelism. In addition, in the MCO-based system-level optimization problem, an absolute value penalty term is introduced to replace the quadratic penalty term to ensure that the problem is a mixed integer linear programming model. This helps improve computational efficiency. Finally, a simulation calculation on a real provincial hydro-thermal power system is carried out to verify the effectiveness of the model and algorithm proposed.
hydro-thermal power system; generator maintenance schedule; scenario-based method; nonanticipative constraints; multi-disciplinary collaborative optimization
10.19783/j.cnki.pspc.211035
2021-08-05;
2021-09-23
代 江(1985—),男,硕士,高级工程师,从事发电调度管理与电力市场相关工作;E-mail: 553097875@qq.com
田年杰(1976—),男,硕士,高级工程师,从事电网运行策划相关工作;E-mail: 370880115@qq.com
姜有泉(1989—),男,硕士,工程师,从事电力市场与电网调度运行相关工作。E-mail: 316286063@qq.com
国家自然科学基金项目资助(52077083);贵州电网有限责任公司科技项目资助(066500KK52190008)
This work is supported by the National Natural Science Foundation of China (No. 52077083).
(编辑 姜新丽)
