云南怒江流域森林地上生物量光学遥感估测及饱和点分析
2022-06-16陆彦羽卢腾飞欧光龙
李 猛 陆彦羽 卢腾飞 胥 辉 欧光龙
(西南林业大学林学院,西南林业大学西南地区生物多样性保育国家林业局重点实验室,云南 昆明 650233)
森林生物量作为森林生态系统的重要属性,是整个森林生态系统运行的能量基础和营养物质来源[1−2]。相较于传统生物量估测的外业周期长、耗时费力、只能获取点上的实测数据、破坏性大等特点[3],森林生物量遥感估测具有费用低、现势性好、准确高效、无破坏、宏观、大尺度动态监测的优势,且各种不同分辨率的多光谱遥感数据已经广泛用于区域及全球森林地上生物量估算研究,较大尺度森林生物量遥感估算已成为森林生物量研究的重要手段[4−7]。在众多的遥感数据源中,光学遥感数据被广泛应用于估测森林生物量[8−10],尤其是Landsat 8 OLI 传感器在波段设置及对植被的敏感性上比之前的TM 传感器有较大的提升且可获取中等和大尺度上的森林资源信息[11]。基于遥感估测森林生物量常用遥感估算经验模型,其主要有线性回归模型,多元回归模型、K−最邻近分类法、人工神经网络法、支持向量机法、随机森林回归、Cubist 回归等模型[12−15]。
目前森林生物遥感估测研究颇多,但森林生物量遥感估测仍具有不确定性[16],不确定性的来源主要有生物量模型预估表现、野外样地数据获取、遥感数据源及其空间分辨率、森林的空间异质性、森林生境信息因子等[17]。其中光学遥感估测的光饱和点带来的不确定性尤受关注[18−19],因为光学遥感数据的信息获取主要来源于森林表层,对森林空间结构信息不敏感[20],在蓄积量较高的区域,冠层的层叠以及物种分布的多样性导致遥感信息饱和,从而出现高值低估的现象[21]。因此确定光饱点对于提高森林生物量遥感估测精度具有重要意义。为确定森林生物量光学遥感估测的光饱和点,已有学者尝试了不同的求解方法,周律等[22]基于空间回归模型运用二次项函数和幂函数求解普洱市思茅松林生物量光饱和点;赵盼盼[23]利用分层理论和半变异函数确定了浙江省6 类森林的生物量光饱和点;他们采用不同的研究方法分析了森林生物量光饱和点,进一步提高了森林生物量的估测精度。但这些研究多聚焦于某一森林类型或平原丘陵等地形相对单一的地区,对于高山峡谷和高森林异质性地区的研究涉及不多。
怒江流域地处中国云南西北部,其北部区域是三江并流的核心区域,具有极其重要的生态地位[24],其特殊高山峡谷地形孕育了完整的植被垂直带谱景观与多种森林植被类型,是全球生物多样性和生态景观保护的重要地域[25]。其复杂的地貌特征导致传统样地实测生物量在此区域难以开展,探索复杂地形的森林生物量光学遥感估测的光饱和点值对于提高区域森林生物量的精确估测具有重要理论和实践意义。鉴于此,本研究以云南省怒江流域为研究对象,基于Landsat 8 数据源,结合地面二调小班数据,开展流域森林地上生物量遥感反演研究以及对生物量光饱和点的确定和不同模型估测生物量的对比分析。在分析地面样地与遥感影像变量相关性基础上,运用参数模型与非参数模型,探讨从样地到区域,点面结合的森林地上生物量估算方法,旨在为我国大范围流域森林生物量估测和森林生物量饱和点的确定提供参考。
1 研究区概况
研究区为怒江流域云南段,地处北纬24°07′~28°23′,东经98°07′~100°00′。怒江全长3 240 km,中国部分长2 013 km,云南省境内段长650 km;流域总面积32.5 万km2,云南省内流域面积3.35 万km2,占云南省面积的8.7%。流域内,日温差大,年温差小,四季不明显,年平均气温在14.8~21.3 ℃,无霜期长,水资源丰富,降水量充足,年均降水量在746.6~2 095.2 mm。云南省怒江流域由其独特的自然条件,造就了其地域的森林类型多样,树种繁多,分布有热带雨林、季雨林、常绿阔叶林、寒温性针叶林等森林类型[26]。怒江流域流经的4 个州市的森林覆盖率均在40%以上,生物多样性丰富,是我国西南地区重要的生态廊道。
2 材料与方法
2.1 小班数据处理
基于研究区2016 年的森林资源二类调查数据,在ArcGIS 10.5 中剔除蓄积量为0 m3和平均胸径小于5 cm 的小班,再通过目视解译,去除非植被的小班。通过所获取的二调数据小班的每公顷蓄积量,计算出研究区每个小班的蓄积量,参考黄从德[27]的蓄积量−生物量转换模型计算各小班森林地上生物量(表1),进而得到小班单位面积生物量。
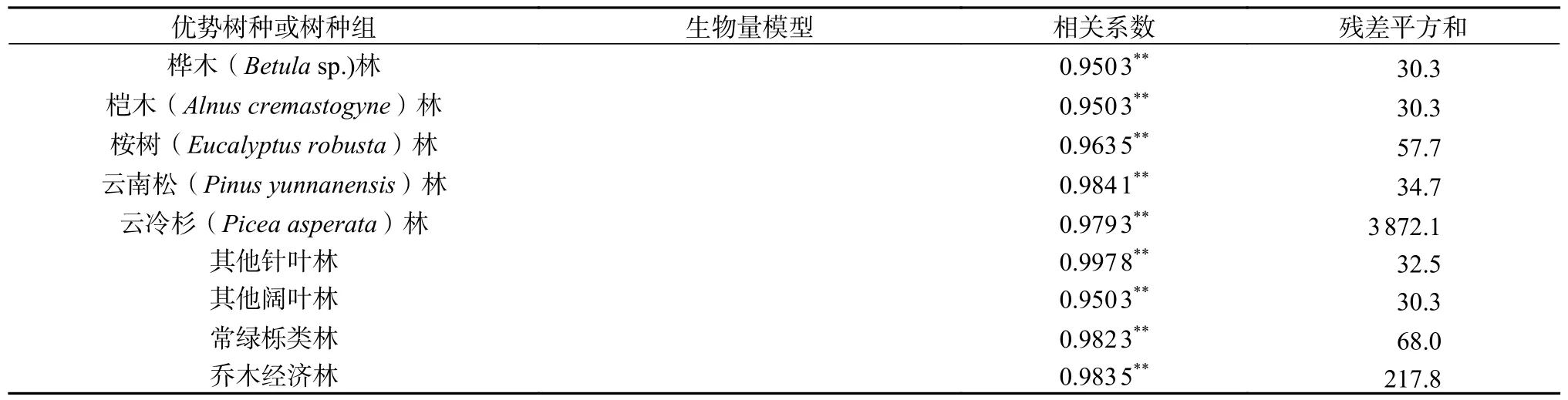
表1 9 类优势树种或树种组的生物量模型Table 1 Biomass models of 9 dominant tree species or tree species groups
基于属性选择划分优势树种或树种组,并将各优势树种或树种组的小班样地在SPSS 23 中采用拉依达准则除去异常值,每类优势树种或树种组均随机筛选不低于1 000 块小班进行分析,并按照7∶3 分别作为建模数据和检验数据(表2)。
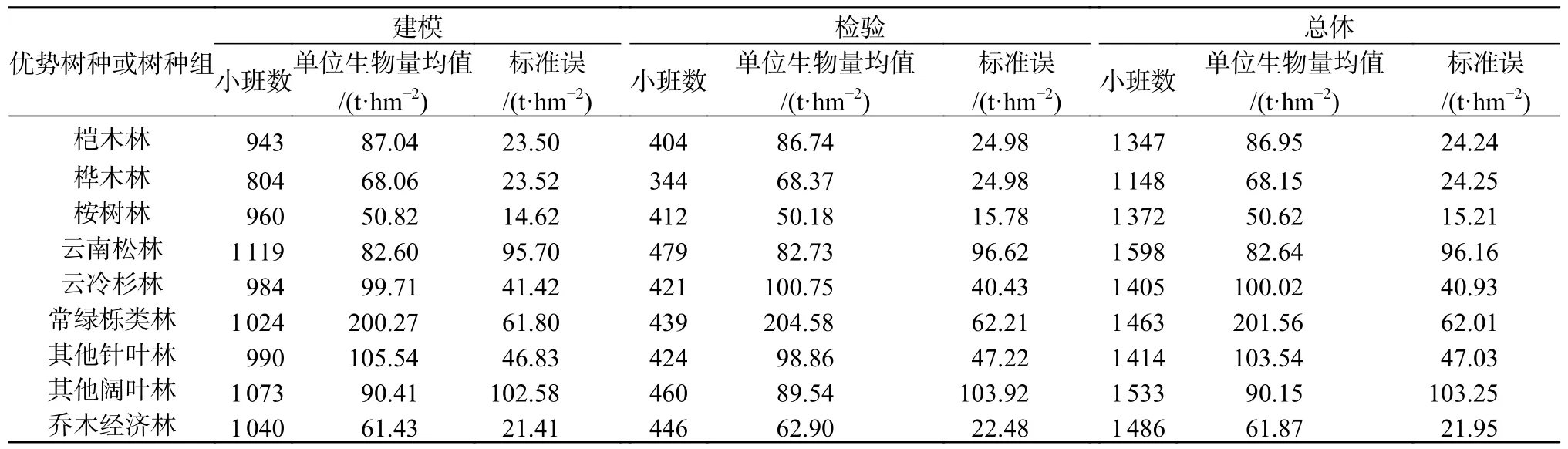
表2 9 类优势树种或树种组的小班情况Table 2 The distribution of small class plot of 9 dominant tree species or tree species groups
2.2 遥感数据来源及处理
在地理空间数据云网站(http://www.gscloud.cn/)下载与二类调查数据同时期的流域区域的Landsat 8 OLI 卫星影像数据(表3),利用ENVI 5.3 进行辐射定标、大气校正、地形校正预处理,进而通过影像融合、裁剪、镶嵌获得研究区预处理后的遥感影像数据。
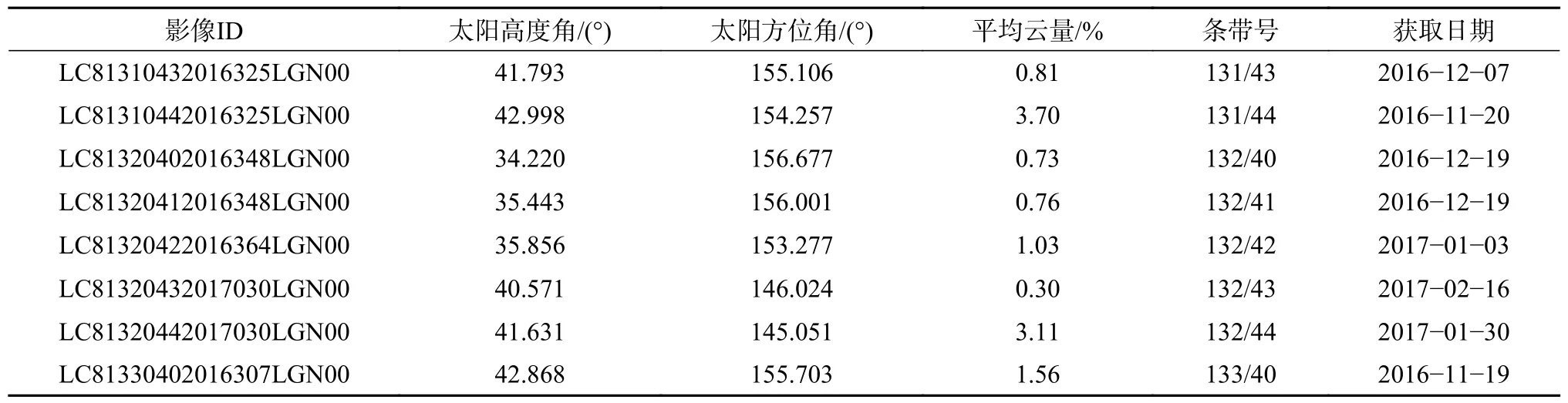
表3 研究区Landsat 8 OLI 影像基本信息Table 3 The basic information of Landsat 8 OLI images in the study area
2.3 遥感因子提取
采用ENVI 5.3 通过波段运算工具Bandmanth提取单波段、植被指数、主成分分析(信息增强)等遥感因子,利用ArcGIS 10.5 分区统计功能统计研究区内各小班遥感因子的均值,将提取的各遥感因子的均值进行相关性分析,选择相关性较高的遥感因子进行模型构建。提取3 类遥感特征因子共36 个,包括:
1)原始单波段因子(7 个)[28]:B1、B2、B3、B4、B5、B6、B7;
2)植被指数(17 个)[10]:归一化植被指数(NDVI、ND43、ND67、ND563、)、差值植被指数(DVI)、土壤调节植被指数(SAVI)、比值植被指数(RVI)、垂直植被指数(PVI)、绿度/亮度/温度植被指数(B/W/G)、大气阻抗植被指数(ARVI)、短红外温度植被指数(MV15)、中红外温度植被指数(MV17)、土壤调整比值植被指数(SARV)、简单比值植被指数(SR)、转型植被指数(TVI)、非线性植被指数(NLI)、优化的简单植被指数(MSR);
3)信息增强因子(12 个)[10]:缨帽K−T 变换因子(KT1/2/3)、主成分因子(PC1−a、PC1−b、PC1−p、PC2−a、PC2−b、PC2−p、PC3−a、PC3−b、PC3−p)。
2.4 森林地上生物量遥感模型
2.4.1 多元线性逐步回归模型
基于SPSS 23 软件采用Pearson 相关系数对遥感变量和森林地上生物量进行相关性分析,剔除P值大于0.05 的遥感变量,选择P值小于等于0.05 的变量进入逐步回归模型参与森林地上生物量的多元线性回归模型构建,并选取方差膨胀因子(VIF)10 进行多重共线性诊断,最终确定参与模型构建的自变量,具体方程为:

式中:Y表示单位森林地上生物量,X1、X2、X3表示影响生物量的自变量因子,ρ1、ρ2、ρ3表示未知参数向量,ε表示误差项,其均值为0 且方差大于0。
2.4.2 BP 神经网络模型
在Matlab 2014 软件中采用3 层BP 神经网络模型,其中输入层的神经元个数为各优势树种或树种组的多元线性逐步回归模型中筛选出的自变量,输出层个数为1,根据相关学者[29]的经验进行隐含层神经元个数的选取,其计算方法见式(2)。

式中:m为隐含层神经元个数;n为输入层神经元个数;l为输出层神经元个数;a 为1~10 的整数。
在进行BP 神经网络构建前应将数据进行归一化处理,以便于数据的单位统一,且神经网络输出层的激活函数的值域,在[0,1]或[−1,1]的区间。输出层所采用的是S 型激活函数,其值域限制在[0,1],因此训练数据的输出要归一化到[0,1]。网络训练的函数采用Traingdx,网络最大训练次数为1 000,学习速率为0.01,目标误差选取0.001、0.005、0.010 与隐含层神经元个数进行组合训练网络。
2.5 模型评价与检验
2.5.1 模型评价
本研究选择模型均方根误差(RMSE)和模型调整决定系数(Rj2)对模型进行精度评价。
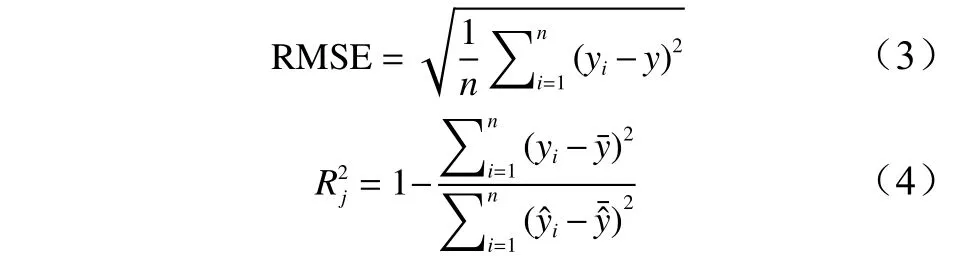
式中:y为观测值;为预测值;为实测值的平均值;为预测值的平均值;n为样本数。
2.5.2 独立性检验
参考李明泽[30]的模型检验方法,选择平均绝对误差(MAE)、平均相对误差(MRE)2 个检验统计量来进行独立性检验。各统计量计算公式如下:
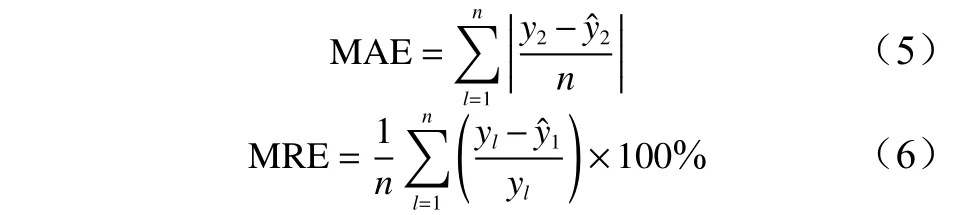
式中:为实测值;为预测值;n为样本总数。
2.5.3 残差分段检验
选取平均残差(ME)和相对平均残差(MRE)2 个指标对建模样本进行分段残差检验,分别设置0~50、50~100、100~150、150~200 t/hm2和200 t/hm2以上5 个生物量段[2]。通过分段残差检验分析不同模型在不同生物量段的残差差异。
2.5.4 研究区9 类优势树种或树种组森林地上生物量反演
依据森林资源二类调查数据获取九类优势树种或树种组的空间分布位置,基于 Landsat8 OLI影像采用像元法计算各小班内九类优势树种或树种组的地上生物量值,再根据不同模型的生物量构建方法对研究区九类优势树种或树种组进行生物量反演。
2.6 生物量光饱和点确定
根据光学遥感不同波段的反射率与植被的关系,确定生物量估测的光饱和点。对9 类优势树种或树种组的生物量与遥感因子各单波段进行相关性分析,选择相关性极显著的波段与生物量建立散点图。一般情况下,波段反射率随着生物量的增大而减小,达到一定值后趋于稳定,这与自变量对因变量的影响随空间距离正向变化相似,因此可通过地统计学的半变异函数求饱和点。半变异的理论模型有:线性、非线性及孔穴效应模型;模型参数:块金值C0、偏基台值C、变程ɑ,在区域化结构性研究中具有非常重要的物理意义[31]。
本研究参考赵盼盼[23]的方法,利用半变异函数非线性模型中的球状模型求解生物量光饱和点。先确定出半变异函数的拟合求解模型参数,再求解出各优势树种或树种组的生物量光饱和值,具体公式如下:
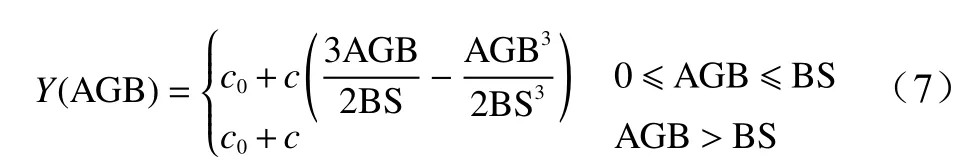
式中:Y(AGB) 为光谱反射率值;c0为生物量值为0 时,光谱反射率的值;c为光谱变化率;c0+c为生物量饱和时光谱反射率的最大或最小值;BS 为参与模型构建波段的光谱饱和值。
3 结果与分析
3.1 森林地上生物量估测模型构建
3.1.1 建模因子筛选
通过Pearson 相关性分析和多重共线性诊断,选取VIF10 的遥感特征变量,结果见表4。桦木林纳入模型构建的遥感因子为B3、B6、B7,桤木林纳入模型构建的遥感因子为B6、B7,桉树林纳入模型构建的遥感因子为PC1−b、MSR,云南松林纳入模型构建的遥感因子为MSR、B5、ND563,云冷杉林纳入模型构建的遥感因子为albedo、MSR、B7、NDVI,乔木经济林纳入模型构建的遥感因子为B6、ARVI,其他阔叶林纳入模型构建的遥感因子为B6、B7,其他针叶林纳入模型构建的遥感因子为PC1−p、MSR、PC2−b、TVI,常绿栎类林纳入模型构建的遥感因子为B6、B7,整体来看9 类优势树种或树种组与单波段遥感因子均呈极显著相关(P0.01),且B6、B7 与各优势树种或树种组的生物量相关性较高。
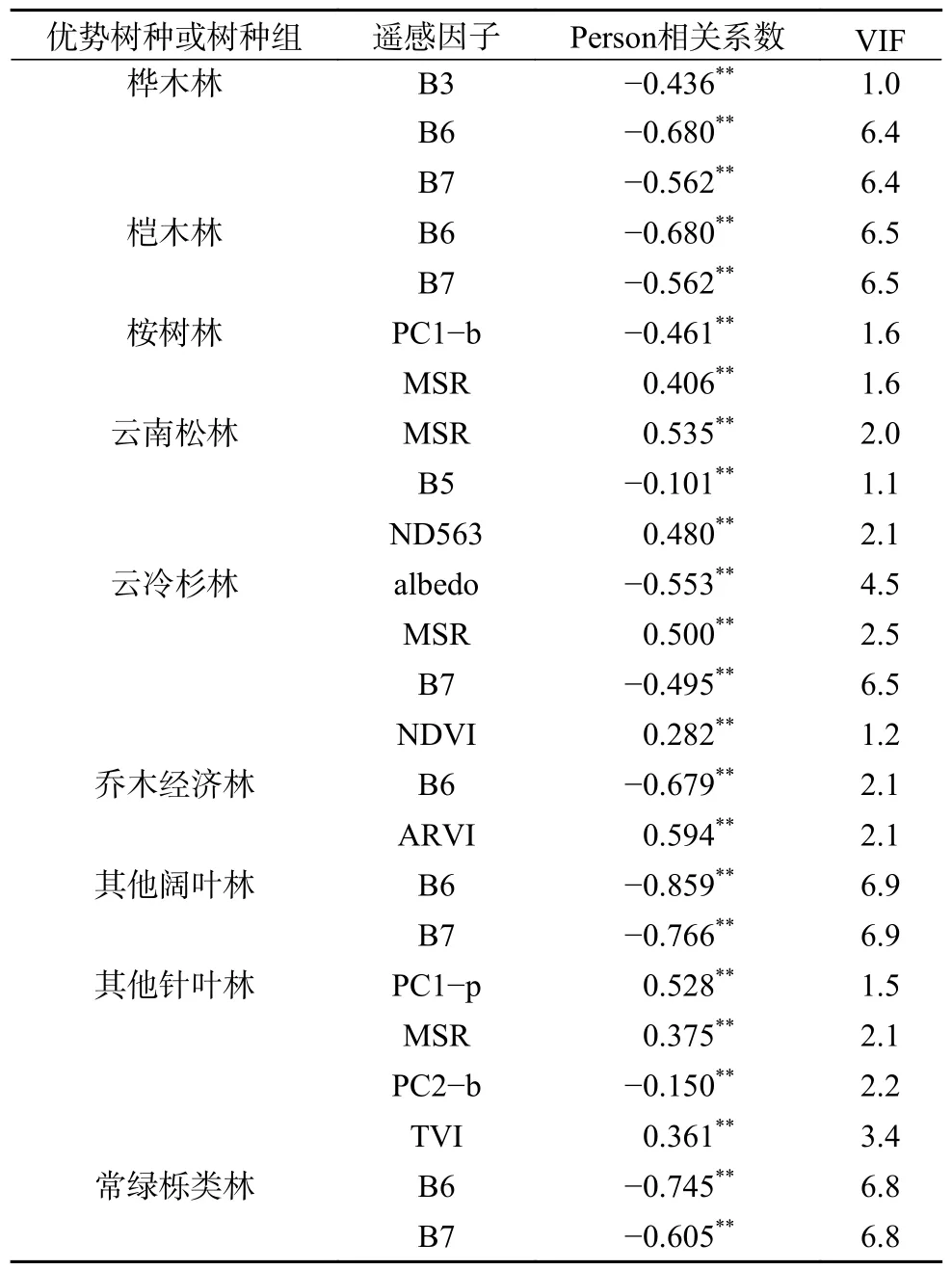
表4 9 类优势树种或树种组的相关性分析及共线性诊断结果Table 4 Correlation analysis and collinearity diagnosis results of 9 dominant tree species or tree species groups
3.1.2 多元线性逐步回归模型构建
由表5 可知,B6、B7 波段和植被指数MSR 被纳入建模较多,表明这3 个遥感因子与植被生物量具有较强的相关性。不同树种或树种组的Rj2也各不相同,其他阔叶林的Rj2最高为0.744;其次是常绿栎类林,Rj2其值为0.650。表明此模型对于两类树种的地上生物量具有最好的模型拟合效果,其模型拟合值与实测值越接近。云南松林、云冷杉林、乔木经济林、其他针叶林、桤木林,这几类森林的Rj2也较好,均在0.3以上,且RSME 的值都相对较低,表明模型对这几类森林的生物量具有较好的模型拟合精度。桦木林的Rj2只有0.189,模型拟合精度最低,表明多元线性逐步回归模型对于计算该地区的桦木林生物量的适用性不强。

表5 9 类树种或树种组逐步线性回归模型构建Table 5 Construction of stepwise linear regression model for 9 species or groups of tree species
3.1.3 BP 神经网络模型构建
BP 神经网络模型评价结果见表6。各优势树种或树种组的神经网络模型的目标误差,隐含层节点数。整体上9 类优势树种或树种组的BP 神经网络模型Rj2均在0.3 以上,桦木林的Rj2最低为0.306、RMSE 为31.628 t/hm2,桉树林的Rj2次低为0.359、RMSE 为26.710 t/hm2,表明BP 神经网络模型对两类树种或树种组的森林的生物量的模型拟合精度较低;对其他几类树种或树种组的森林的生物量的模型拟合精度较高,最高的为其他阔叶林,Rj2最高为0.815,RMSE 为8.089 t/hm2。
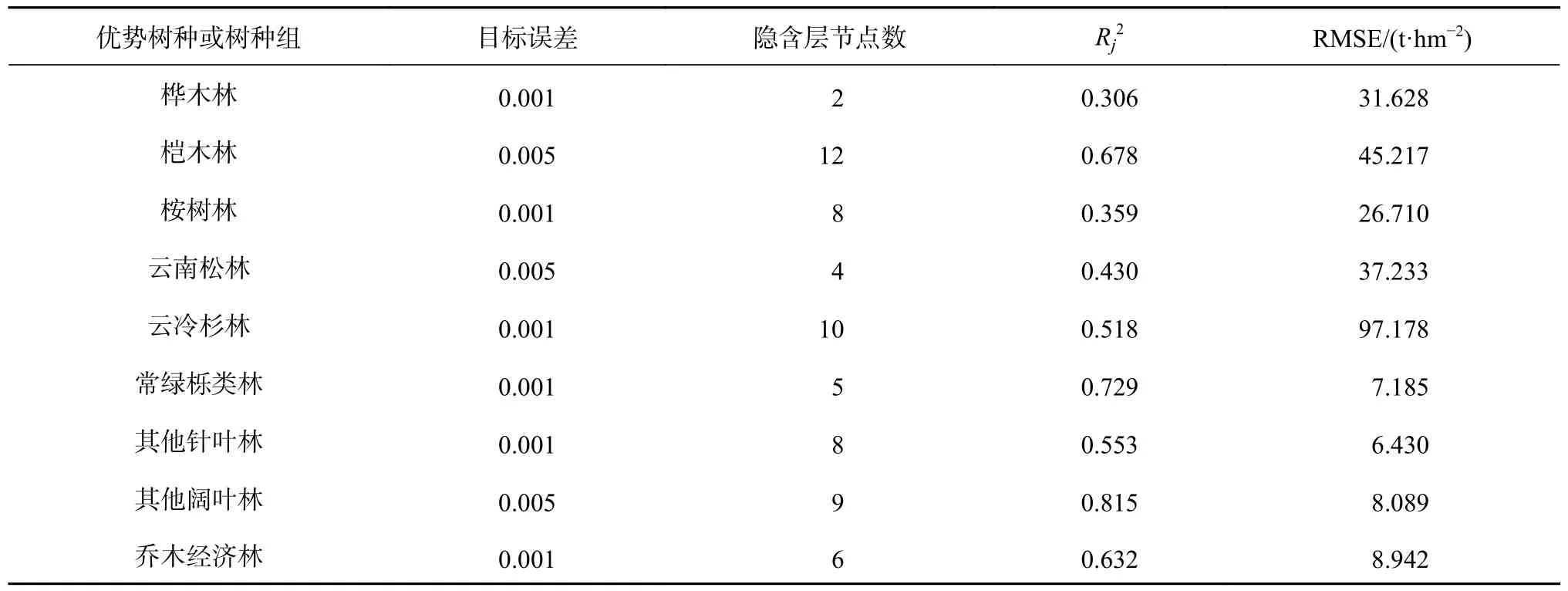
表6 9 类优势树种或树种组的BP 神经网络模型参数Table 6 BP neural network model parameters of 9 dominant species or groups of tree species
3.2 模型精度评价
由表7 可知,各优势树种或树种组的BP-神经网络模型R2均比多元线性逐步回归模型的高;从RMSE 来看,相较于多元线性逐步回归模型,BP-神经网络模型对于其他阔叶林和其他针叶林、常绿栎类林、乔木经济林的生物量估测有着更高的估测精度和较低的估测误差,两模型对于桉树林与桦木林的模型精度都较低。从独立性指标来看,2 种模型除了桦木林外,其他树种的独立性检验结果都比较好,其中两模型的独立性检验结果最优的树种为常绿栎类林。
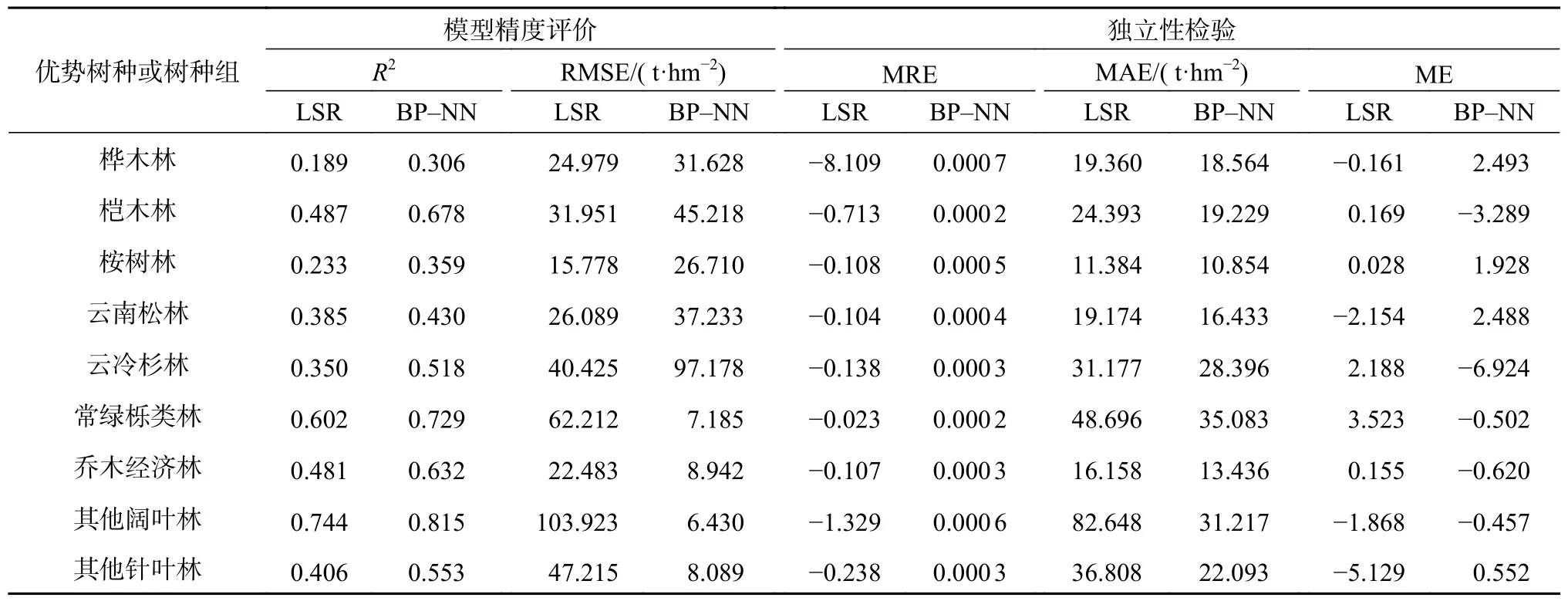
表7 9 类优势树种或树种组多元回归模型和BP 神经网络模型精度评价结果Table 7 Accuracy evaluation results of multiple regression models for 9 dominant species or groups of tree species
相较于逐步线性回归模型,BP-NN 神经网络模型对于各优势树种或树种组的生物量估测更接近实测值,估测精度更高,其生物量的估测更为准确,因此BP 神经网络模型的估测能力更优于逐步线性回归。
3.3 生物量分段残差分析
生物量分段残差结果见表8。由表8 可知,整体上BP 神经网络模型的预估精度较高,误差相对逐步回归模型较小。从生物量分段看,2 种模型均存在生物量低值高估和高值低估的情况,尤其常绿栎类林的逐步回归模型估测,在所有生物量分段中均显示为低值高估,且存在过度估计的情况;云冷杉林的BP 神经网络模型估测,在所有生物量分段中均显示为高值低估。在低生物量段(100 t/hm2)时,BP 神经网络模型的估测能力强于逐步回归模型,且前者ME 值更低了。在150 t/hm2的2 个生物量分段中,除了逐步回归模型估测的常绿栎类林的ME 和MRE 为负值外,其余均为正值,且BP 神经网络模型除其他阔叶林和常绿栎类林外,其他树种或树种组的ME 均大于70 t/hm2,出现显著的高值低估情况,说明在高生物量段2 种模型估测能力均显不足。总体来看,虽然2 种模型均出现了过高估计和过低估计,但是BP 神经网络模型相较于逐步回归模型具有较好的预估精度。
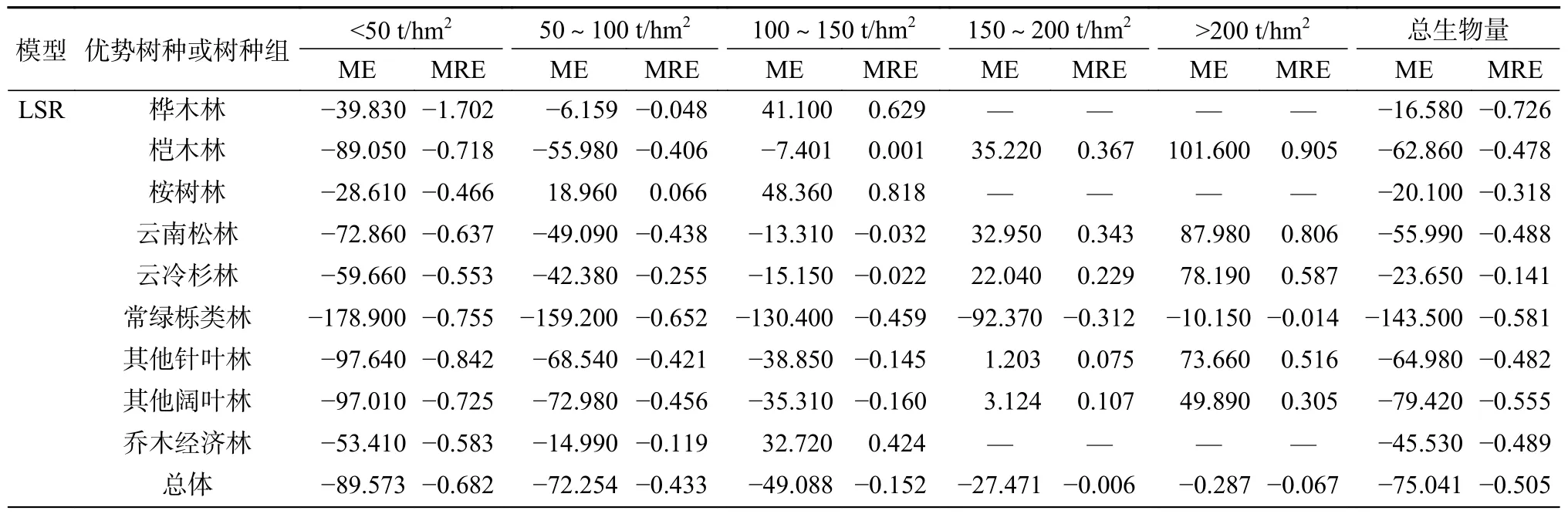
表8 生物量分段残差分析Table 8 Biomass segmentation error results
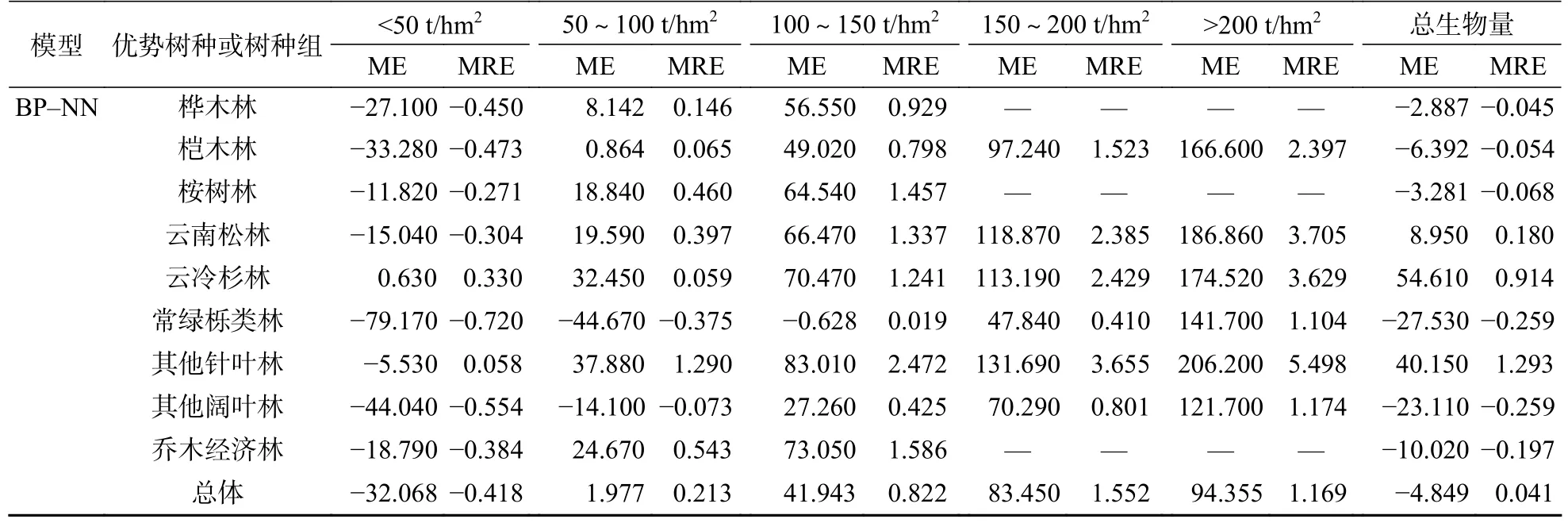
续表 8
3.4 9 类优势树种或树种组的森林地上生物量反演
怒江流域9 类优势树种或树种组以及总的森林地上生物量反演统计量见表9。由表9 可知,2 种模型反演的9 类优势树种或树种组生物量估测值总体上大于实际测测量的生物量值,但BP 神经网络模型的生物量估测值更接近实际值,且BP 神经网络模型估测生物量的均方根误差均比逐步回归模型的小,因此BP 神经网络模型的估测精度优于逐步线性回归模型,其估测值更加真实。
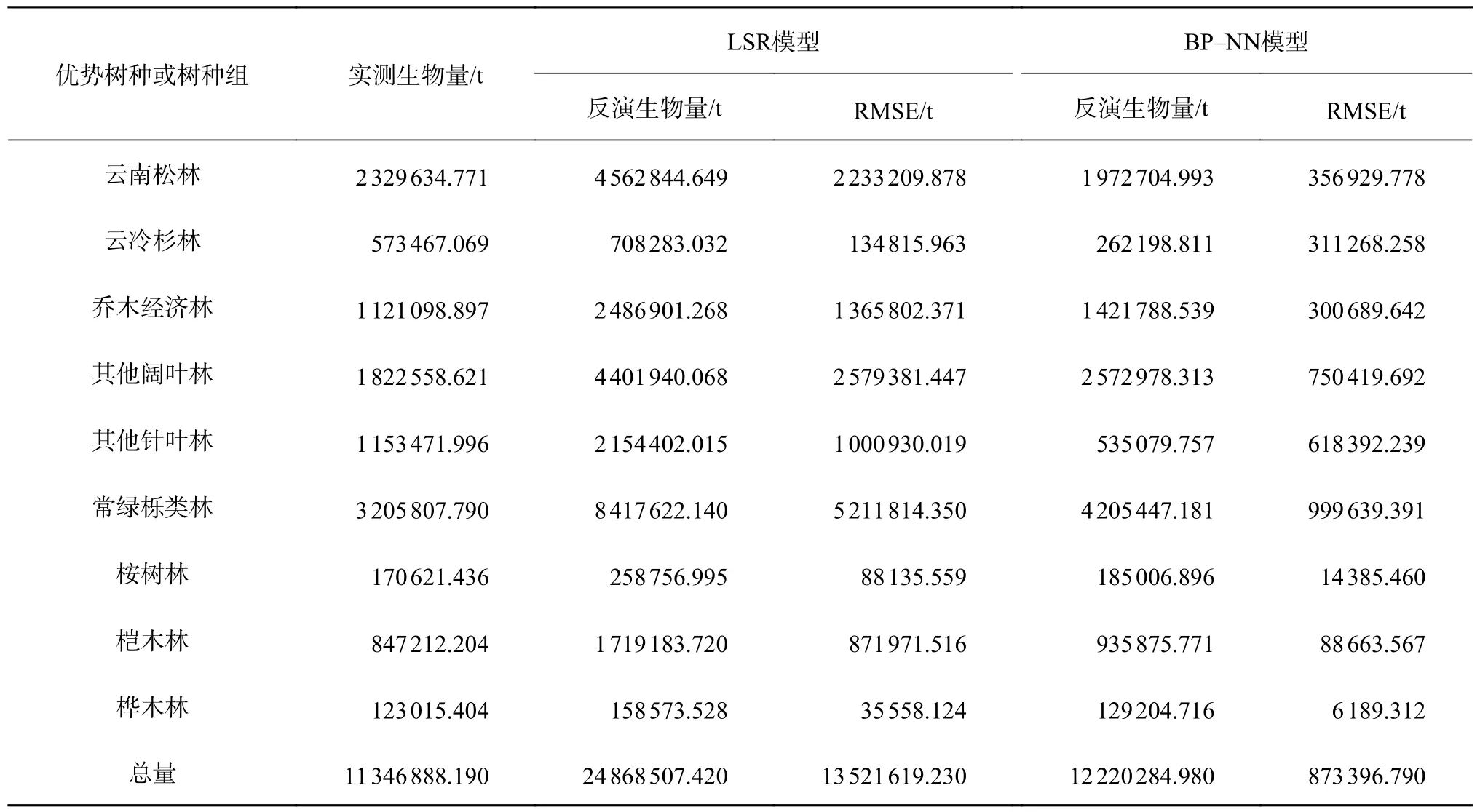
表9 2 种模型下9 类优势树种或树种组的生物量反演值Table 9 Biological inversion of 9 dominant species or groups of tree species under 2 models
怒江流域生物量反演结果见图1。由图1 可知,2 种模型下怒江流域的云南松林的生物量主要分布在0~50 t/hm2,少数分布在50~150 t/hm2;云冷杉林生物量分布在0~100 t/hm2;常绿栎类林生物量主要分布在50~150 t/hm2;桉树林生物量估测主要分布在0~50 t/hm2,少数分布在50~100 t/hm2;桤木林生物量主要分布在50~150 t/hm2,少数分布在150~200 t/hm2;桦木林生物量主要分布在50~150 t/hm2;乔木经济林生物量主要分布在30~100 t/hm2;其他阔叶林生物量主要分布在50~150 t/hm2;其他针叶林生物量主要分布在0~100 t/hm2,少数分布在100~300 t/hm2。从整体空间分布来看,怒江流域9 类优势树种或树种组的森林地上生物量高生物量200 t/hm2主要分布在流域中西部区域和北部边缘地区,生物量50~200 t/hm2集中分布于怒江流域的中部地区,且分布区域较广。
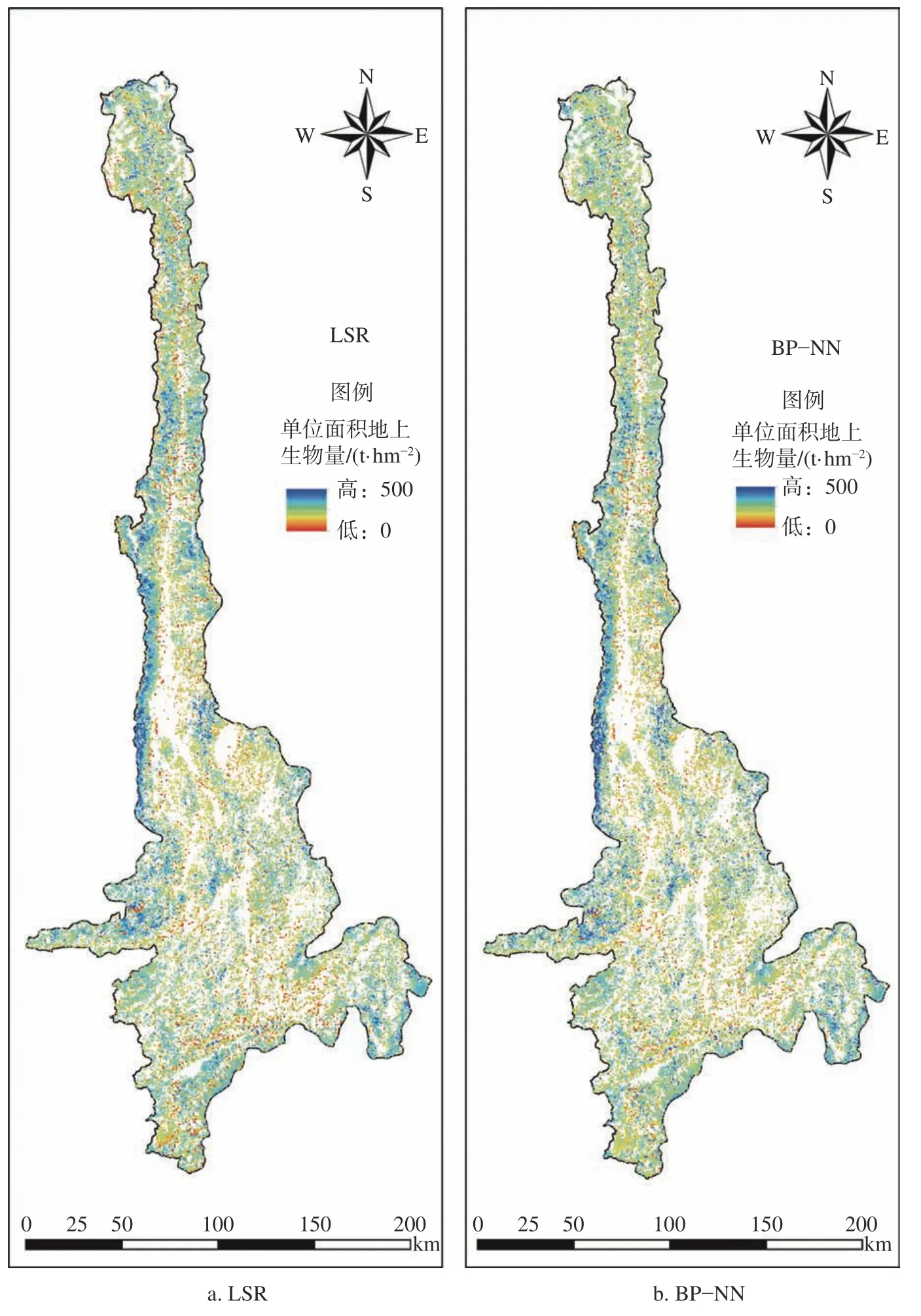
图1 研究区2 种模型反演的森林地上生物量密度分布Fig.1 The inversion map of aboveground biomass density using 2 models
3.5 森林地上生物量遥感估测光饱和点分析
对9 类优势树种或树种组的生物量与遥感因子各单波段进行相关性分析,得到云南松林生物量与B3 波段相关性最高,值为−0.534;云冷杉生物量与B3 波段相关性最高,值为−0.537;常绿栎类林生物量与B6 波段相关性最高,值为−0.745;桉树林生物量与B6 波段相关性最高,值为−0.458;桤木生物量与B6 波段相关性最高,值为−0.680;桦木生物量与B3 波段相关性最高,值为−0.436;乔木经济林生物量与B6 波段相关性最高,值为−0.679;其他针叶林生物量与B6 波段相关性最高,值为−0.502;其他阔叶林生物量与B6 波段相关性最高,值为−0.859。基于此,本研究选择相关性极显著的波段与9 类优势树种或树种组的生物量建立散点图(图2),由图2 可知,与9 类优势树种或树种组的生物量相关性最高的波段反射率值都随着生物量的增加而降低,随着生物量增加达到一定值时,波段光谱反射率值趋于平稳或出现拐点,该值即为生物量光饱和值。
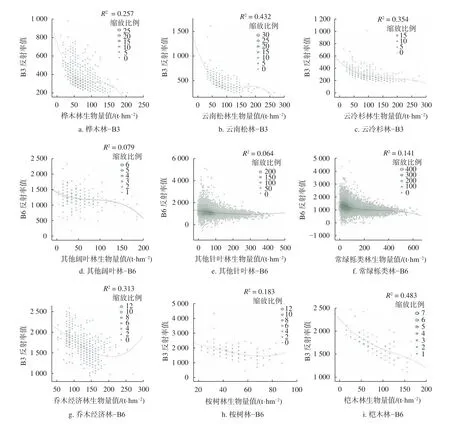
图2 9 类优势树种或树种组的生物量与对应单波段间的散点图Fig.2 Discatter between biomass and corresponding bands of 9 dominant species or groups of tree species
半变异函数模型极其评价见表10。由表10可知,不同的树种或树种组具有不同的光饱和值和相关系数,云冷杉林的生物量饱和值最大,为197 t/hm2;云南松林、其他针叶林、桤木林的饱和值次之;乔木经济林、常绿栎类林、其他阔叶林的饱和值较小。其中桉树林的饱和值最低,为70 t/hm2;桤木林的调整R2最高,为0.469;其他阔叶林的调整R2最低,为0.071。
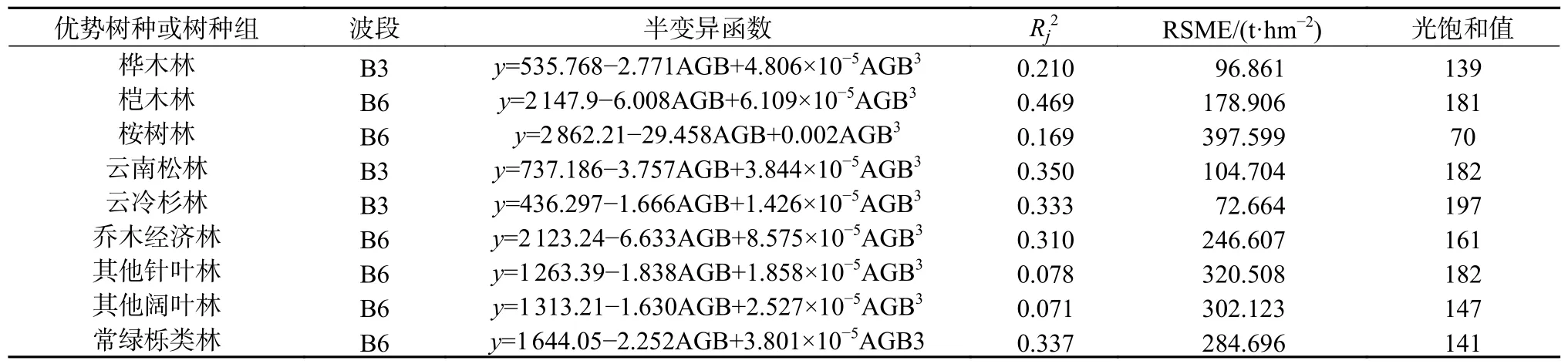
表10 半变异函数求解的九类优势树种或树种组森林光饱和值Table 10 The forest light saturation values of 9 dominant tree species or tree species groups solved by semi variogram
4 结论与讨论
光学遥感估测森林地上生物量普遍存在森林林生物量光饱和点的现象[22],同一区域不同的森林类型,相同类型不同的分布区的森林,同一森林中不同树种之间,其生物量的光饱和值不同[17],本研究通过对9 类树种或树种组进行半变异函数求解,参数方程组合,求出各树种或树种组的光学遥感估测森林生物量光饱和值,云南松林182 t/hm2,云冷杉林197 t/hm2,乔木经济林161 t/hm2,其他针叶林182 t/hm2,其他阔叶林147 t/hm2,常绿栎类林141 t/hm2,桉树林70 t/hm2,桦木139 t/hm2,桤木林181 t/hm2。该值高于赵盼盼[23]研究所得的森林生物量光饱和值(马尾松林159 t/hm2;杉木林143 t/hm2;阔叶树林123 t/hm2)。这是因为森林生物量光饱和值受森林植被类型,森林异质性的影响[17],其中森林异质性是导致遥感估测光饱和点存在的主要原因[12,18,32]。怒江流域地处云南滇西北高山峡谷区,森林类型多样,树种丰富,各树种之间的林分结构差异大,森林异质性高,另外受地形因子的影响,研究区垂直气候分带明显,海拔差异巨大,直接造成研究区各树种或树种之间的分布差异性巨大,光学遥感估测森林生物量的光饱和值高于赵盼盼的森林生物量光饱和值。光学遥感估测森林生物量普遍存在生物量光饱和点的现象,如何解决光饱点问题依然是今后的研究热点,今后可以结合多源遥感数据构建模型估测生物量以期减少生物量光饱的问题。
由于受分布区和树种特性的生长习性的影响,桦木林、桉树林、其他针叶林、其他阔叶林的生物量遥感估测的光饱和点模拟结果的R2小于0.3,模型解释的信息不大,这可能与分布面积较小,小班样本量不足有关;但为了获得研究区所有森林类型的森林地上生物量遥感估测的光饱和点值及生物量模型,进而获得整个研究区的森林地上生物量遥感估测数据,本文仍然将其纳入一并研究,由于其分布面积较小,对整个研究区森林生物量遥感估测的影响不大;面积较小的林分地上生物量遥感光饱和值及高精度估测模型仍需在今后的研究中进一步探索。
本研究采用参数模型中的多元性线逐步回归模型和非参数模型中的BP 神经网络模型进行生物量遥感估测,从模型独立性检验来看,BP 神经网络模型下各优势树种或树种组的R2都比逐步性线回归模型下的高,表明BP 神经网络模型的估测精度高于逐步线性回归模型的估测精度,这与徐辉等[33]、张锋[13]、翟晓江[34]的研究结果一致。从生物量残差分段分析表明来看,两模型均存在低值高估和高值低估的情况,这是由于光学遥感数据存在饱和问题,在生物量高的森林中出现高值低估的情况,另外,由于一些林间空地等会影响光学遥感的反射率,使得在低生物量的森林中生物量被高估[32]。但是总体上,不同的优势树种或树种组BP 神经网络模型在所有生物量分段上ME 和MRE 优于一般逐步回归模型,可见BP 神经网络模型有着更为理想的模型预测能力,且在一定程度上能够减小数据饱和引起的估测误差。
本研究选用的地面数据是怒江流域2016 年森林资源的二类调查小班数据,与实测样地点数据不同的是其更容易获取且分布范围广样本量充足,其可以弥补高山峡谷地区样本数据不足的缺陷,卢腾飞等[2]、周律等[22]采用森林资源二调小班数据获取小班数据遥感特征因子参与模型构建估测森林生物量得到较好的结果,表明可以使用二调小班数据作为遥感估测森林生物量的地面数据。本研究采用二调小班数据,构建多元性线逐步回归模型和BP 神经网络模型进行生物量遥感估测,进行模型精度评价和生物量残差分析以及生物量反演,其结果和多数学者的相似,也进一步表明使用二调小班数据作为遥感估测森林生物量的地面数据是可靠的。
